6.3: Kiasi cha Mapinduzi - Shells za Cyl

Last updated
Save as PDF

Page ID: 178284

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Tumia kiasi cha imara ya mapinduzi kwa kutumia njia ya shells za cylindrical.
Linganisha njia tofauti za kuhesabu kiasi cha mapinduzi.

Katika sehemu hii, tunachunguza njia ya shells za cylindrical, njia ya mwisho ya kutafuta kiasi cha imara ya mapinduzi. Tunaweza kutumia njia hii kwa aina hiyo ya yabisi kama njia ya disk au njia ya washer; hata hivyo, kwa njia za disk na washer, tunaunganisha pamoja na mhimili wa kuratibu sambamba na mhimili wa mapinduzi. Kwa njia ya shells za cylindrical, tunaunganisha pamoja na mhimili wa kuratibu perpendicular kwa mhimili wa mapinduzi. Uwezo wa kuchagua aina gani ya ushirikiano tunayotaka kutumia inaweza kuwa faida kubwa na kazi ngumu zaidi. Pia, jiometri maalum ya imara wakati mwingine hufanya njia ya kutumia shells za cylindrical zaidi ya kuvutia kuliko kutumia njia ya washer. Katika sehemu ya mwisho ya sehemu hii, tunaangalia njia zote za kutafuta kiasi ambacho tumejifunza na kuweka miongozo fulani ili kukusaidia kuamua njia gani ya kutumia katika hali fulani.

Njia ya Shells za Cylindrical

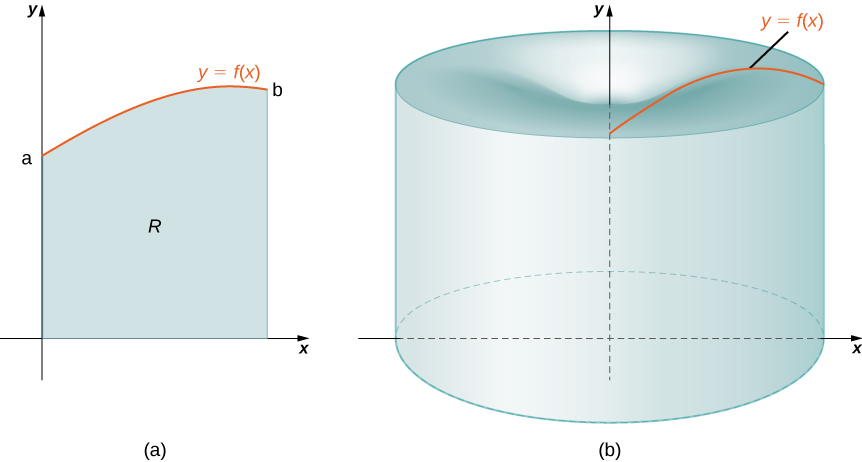
Tena, sisi ni kazi na imara ya mapinduzi. Kama hapo awali, tunafafanua kanda$R$, imefungwa hapo juu na grafu ya kazi$y=f(x)$, chini na $x$-axis, na upande wa kushoto na kulia na mistari$x=a$ na$x=b$, kwa mtiririko huo, kama inavyoonekana kwenye Mchoro$\PageIndex{1a}$. Sisi kisha zinahusu eneo hili kuzunguka$y$ -axis, kama inavyoonekana katika Kielelezo$\PageIndex{1b}$. Kumbuka kuwa hii ni tofauti na yale tuliyofanya kabla. Hapo awali, mikoa iliyofafanuliwa kwa suala la kazi za$x$ zilikuwa zimezunguka $x$-axis au mstari unaofanana nayo.

Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ni safu inayoongezeka katika quadrant ya kwanza. Curve inaitwa “y=f (x)”. Curve huanza kwenye y-mhimili katika y = a. chini ya Curve, juu ya x-axis ni kanda kivuli kinachoitwa “R”. Eneo la kivuli limepakana upande wa kulia na mstari x=b. grafu ya pili ni tatu dimensional imara. Imeundwa kwa kupokezana eneo la kivuli kutoka “a” karibu na mhimili wa y. — Kielelezo$\PageIndex{1}$: (a) mkoa imepakana na graph ya kazi ya$x$. (b) Imara ya mapinduzi yaliyoundwa wakati mkoa unazunguka **$y$-axis.**

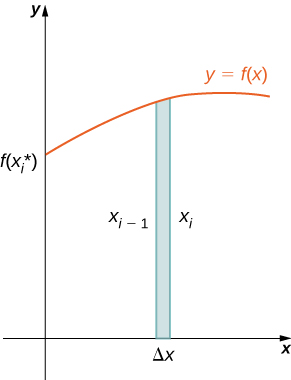
Kama tulivyofanya mara nyingi kabla,$[a,b]$ ugawanye muda kwa kutumia sehemu ya kawaida,$P={x_0,x_1,…,x_n}$ na$i=1,2,…,n$, kwa, chagua uhakika$x^∗_i∈[x_{i−1},x_i]$. Kisha, jenga mstatili juu ya muda$[x_{i−1},x_i]$ wa urefu$f(x^∗_i)$ na upana$Δx$. Mstatili wa mwakilishi unaonyeshwa kwenye Kielelezo$\PageIndex{2a}$. Wakati mstatili huo unazunguka$y$ -axis, badala ya disk au washer, tunapata shell ya cylindrical, kama inavyoonekana kwenye Mchoro$\PageIndex{2}$.

Takwimu hii ina picha mbili. Ya kwanza ni shell ya cylindrical, mashimo katikati. Ina mhimili wima katikati. Pia kuna curve ambayo hukutana juu ya silinda. Picha ya pili ni seti ya mitungi ya makini, moja ndani ya nyingine inayounda kiota cha mitungi. — Kielelezo$\PageIndex{2}$: (a) Mstatili wa mwakilishi. (b) Wakati mstatili huu unazunguka **$y$-axis**, matokeo yake ni shell ya cylindrical. (c) Tunapoweka maganda yote pamoja, tunapata makadirio ya imara ya awali.

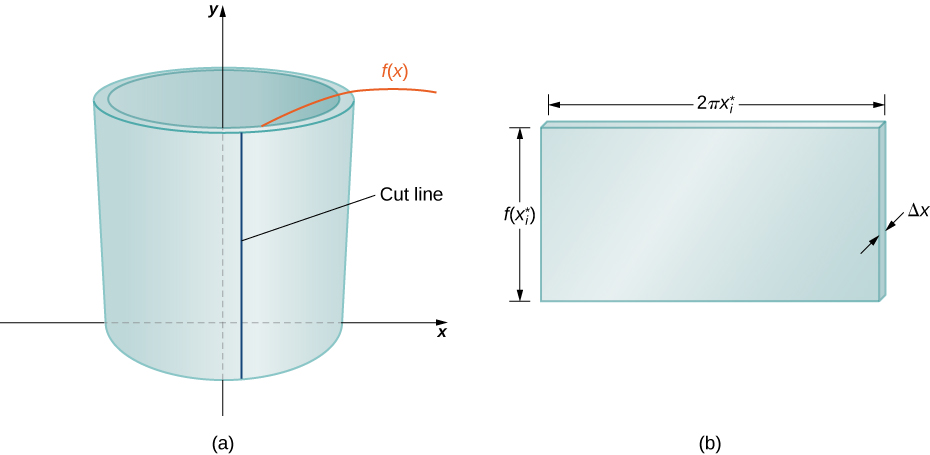
Ili kuhesabu kiasi cha shell hii, fikiria Kielelezo$\PageIndex{3}$.

Takwimu hii ni grafu katika quadrant ya kwanza. Curve inaongezeka na kinachoitwa “y=f (x)”. Curve huanza kwenye mhimili wa y saa f (x*). Chini ya pembe ni mstatili wa kivuli. Mstatili huanza kwenye mhimili wa x. Upana wa mstatili ni delta x. pande mbili za mstatili ni kinachoitwa “xsub (i-1)” na “xsubi”. — Kielelezo$\PageIndex{3}$: Kuhesabu kiasi cha shell.

Ganda ni silinda, hivyo kiasi chake ni eneo la msalaba lililoongezeka kwa urefu wa silinda. Sehemu za msalaba ni annuli (mikoa yenye umbo la pete-kimsingi, miduara yenye shimo katikati), na radius ya nje$x_i$ na radius ya ndani$x_{i−1}$. Hivyo, eneo la msalaba ni$πx^2_i−πx^2_{i−1}$. Urefu wa silinda ni$f(x^∗_i).$ Kisha kiasi cha shell ni

\[ \begin{align*} V_{shell} =f(x^∗_i)(π\,x^2_{i}−π\,x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x^2_i−x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)(x_i−x_{i−1}). \end{align*}\]

Kumbuka kwamba$x_i−x_{i−1}=Δx,$ hivyo tuna

\[V_{shell}=2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)\,Δx. \nonumber \]

Zaidi ya hayo,$\dfrac {x_i+x_{i−1}}{2}$ ni wote midpoint ya muda$[x_{i−1},x_i]$ na Radius wastani wa shell, na tunaweza takriban hii kwa$x^∗_i$. Sisi basi

\[V_{shell}≈2π\,f(x^∗_i)x^∗_i\,Δx. \nonumber \]

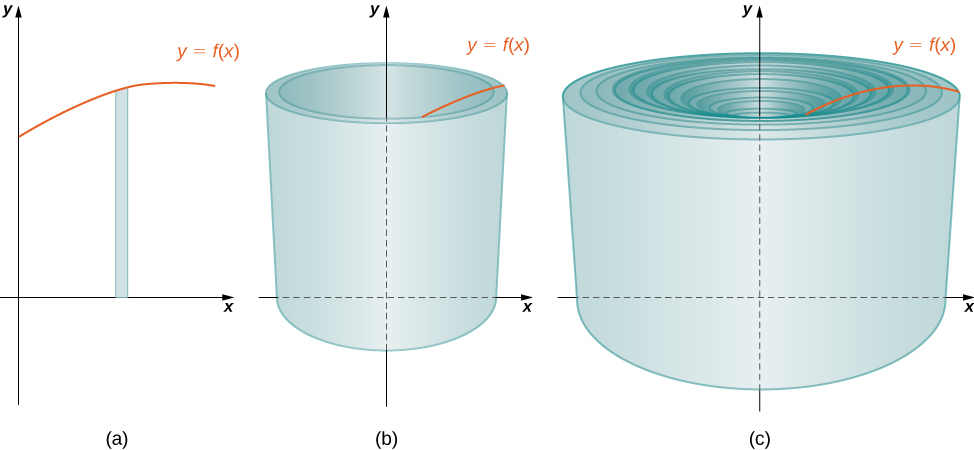
Njia nyingine ya kufikiri juu ya hili ni kufikiri ya kufanya kukata wima kwenye shell na kisha kuifungua ili kuunda sahani ya gorofa (Kielelezo$\PageIndex{4}$).

Takwimu hii ina picha mbili. Ya kwanza inaitwa “a” na ni ya silinda ya mashimo karibu na mhimili wa y. Kwenye mbele ya silinda hii ni mstari wa wima unaoitwa “mstari wa kukata”. Urefu wa silinda ni “y=f (x)”. Takwimu ya pili inaitwa “b” na ni block kivuli cha mstatili. Urefu wa mstatili ni “f (x*), upana wa mstatili ni “2pix*”, na unene wa mstatili ni “delta x”. — Kielelezo$\PageIndex{4}$: (a) Fanya kata ya wima katika shell ya mwakilishi. (b) Fungua shell ili kuunda sahani ya gorofa.

Kwa kweli, radius ya nje ya shell ni kubwa kuliko radius ya ndani, na hivyo makali ya nyuma ya sahani itakuwa kidogo zaidi kuliko makali ya mbele ya sahani. Hata hivyo, tunaweza takriban shell iliyopigwa na safu ya gorofa ya urefu$f(x^∗_i)$, upana$2πx^∗_i$, na unene$Δx$ (Kielelezo). Kiasi cha shell, basi, ni takriban kiasi cha sahani ya gorofa. Kuzidisha urefu, upana, na kina cha sahani, tunapata

\[V_{shell}≈f(x^∗_i)(2π\,x^∗_i)\,Δx, \nonumber \]

ambayo ni formula sawa tulikuwa kabla.

Ili kuhesabu kiasi cha imara nzima, sisi kisha kuongeza kiasi cha shells zote na kupata

\[V≈\sum_{i=1}^n(2π\,x^∗_if(x^∗_i)\,Δx). \nonumber \]

Hapa tuna mwingine jumla Riemann, wakati huu kwa ajili ya kazi$2π\,x\,f(x).$ Kuchukua kikomo kama$n→∞$ inatupa

\[V=\lim_{n→∞}\sum_{i=1}^n(2π\,x^∗_if(x^∗_i)\,Δx)=\int ^b_a(2π\,x\,f(x))\,dx. \nonumber \]

Hii inasababisha utawala wafuatayo kwa njia ya shells za cylindrical.

Kanuni: Njia ya Shells za Cylindrical

Hebu$f(x)$ uendelee na usio na hasi. Kufafanua$R$ kama kanda imepakana juu na grafu ya$f(x)$, chini na $x$-axis, upande wa kushoto na mstari$x=a$, na upande wa kulia na mstari$x=b$. Kisha kiasi cha imara ya mapinduzi yaliyoundwa na$R$ kuzunguka$y$ -axis hutolewa na

\[V=\int ^b_a(2π\,x\,f(x))\,dx. \nonumber \]

Sasa hebu fikiria mfano.

Mfano$\PageIndex{1}$: The Method of Cylindrical Shells I

Eleza$R$ kama eneo lililofungwa hapo juu na grafu ya$f(x)=1/x$ na chini na $x$-axis juu ya muda$[1,3]$. Pata kiasi cha imara ya mapinduzi yaliyoundwa na$R$ yanazunguka$y$ -axis.

Suluhisho

Kwanza ni lazima graph kanda$R$ na kuhusishwa imara ya mapinduzi, kama inavyoonekana katika Kielelezo$\PageIndex{5}$.

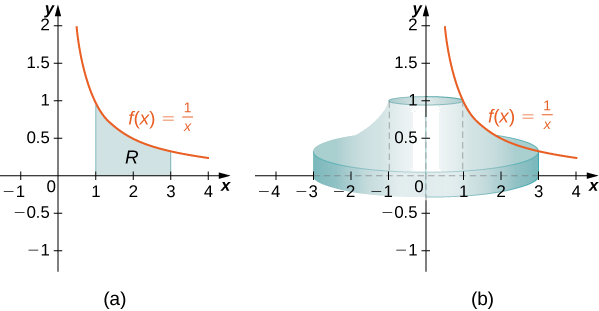
Takwimu hii ina picha tatu. Ya kwanza ni imara ambayo imeundwa kwa kupokezana pembe y=1/x kuhusu mhimili y. Mango huanza kwenye x-axis na ataacha ambapo y=1. Picha ya pili inaitwa “a” na ni grafu ya y=1/x katika roboduara ya kwanza. Chini ya curve ni kanda kivuli kinachoitwa “R”. Mkoa umepakana na pembe, x-axis, upande wa kushoto saa x=1 na kulia saa x=3. Picha ya tatu inaitwa “b” na ni nusu ya imara iliyoundwa kwa kupokezana eneo la kivuli kuhusu mhimili wa y. — Kielelezo$\PageIndex{5}$: (a) Eneo$R$ chini ya grafu ya$f(x)=1/x$ zaidi ya muda$[1,3]$. (b) Imara ya mapinduzi yanayotokana na yanazunguka$R$ kuhusu$y$ -axis.

Kielelezo$\PageIndex{5}$ (c) Kutazama imara ya mapinduzi na CalcPlot3D.

Kisha kiasi cha imara kinatolewa na

\[ \begin{align*} V =\int ^b_a(2π\,x\,f(x))\,dx \\ =\int ^3_1\left(2π\,x\left(\dfrac {1}{x}\right)\right)\,dx \\ =\int ^3_12π\,dx\\ =2π\,x\bigg|^3_1=4π\,\text{units}^3. \end{align*}\]

Zoezi$\PageIndex{1}$

Eleza R kama eneo lililofungwa hapo juu na grafu ya$f(x)=x^2$ na chini na$x$ -axis juu ya muda$[1,2]$. Pata kiasi cha imara ya mapinduzi yaliyoundwa na$R$ yanazunguka$y$ -axis.

Kidokezo: Tumia utaratibu kutoka kwa Mfano$\PageIndex{1}$.

Jibu: $\dfrac{15π}{2} \, \text{units}^3 $

Mfano$\PageIndex{2}$: The Method of Cylindrical Shells II

Eleza$R$ kama eneo lililofungwa hapo juu na grafu ya$f(x)=2x−x^2$ na chini na$x$ -axis juu ya muda$[0,2]$. Pata kiasi cha imara ya mapinduzi yaliyoundwa na$R$ yanazunguka $y$-axis.

Suluhisho

Kwanza graph kanda$R$ na kuhusishwa imara ya mapinduzi, kama inavyoonekana katika Kielelezo$\PageIndex{6}$.

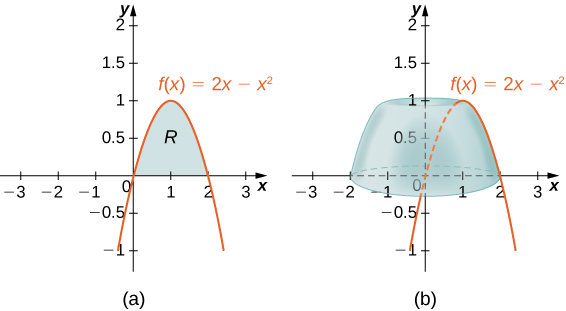
Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ni safu f (x) =2x-x ^ 2. Ni kichwa chini parabola intersecting x-axis katika ant asili katika x=2. Chini ya pembe kanda katika roboduara ya kwanza ni kivuli na inaitwa “R”. Takwimu ya pili ni grafu ya safu sawa. Kwenye grafu ni imara inayoundwa na mzunguko kanda kutoka “a” kuhusu mhimili wa y. — Kielelezo$\PageIndex{6}$: (a) kanda$R$ *chini ya grafu ya$f(x)=2x−x^2$* *zaidi ya muda$[0,2].$* *(b) kiasi cha mapinduzi kupatikana kwa yanazunguka* *$R$*kuhusu$y$ -axis*.*

Kisha kiasi cha imara kinatolewa na

\[\begin{align*} V =\int ^b_a(2π\,x\,f(x))\,dx \\ =\int ^2_0(2π\,x(2x−x^2))\,dx \\ = 2π\int ^2_0(2x^2−x^3)\,dx \\ =2π \left. \left[\dfrac {2x^3}{3}−\dfrac {x^4}{4}\right]\right|^2_0 \\ =\dfrac {8π}{3}\,\text{units}^3 \end{align*}\]

Zoezi$\PageIndex{2}$

Eleza$R$ kama eneo lililofungwa hapo juu na grafu ya$f(x)=3x−x^2$ na chini na$x$ -axis juu ya muda$[0,2]$. Pata kiasi cha imara ya mapinduzi yaliyoundwa na$R$ yanazunguka$y$ -axis.

Kidokezo

Tumia mchakato kutoka Mfano$\PageIndex{2}$.

Jibu

$8π \, \text{units}^3 $

Kama ilivyo kwa njia ya disk na njia ya washer, tunaweza kutumia njia ya maganda ya cylindrical na yabisi ya mapinduzi, ilizunguka$x$ -axis, wakati tunataka kuunganisha kwa heshima na$y$. Utawala sawa wa aina hii ya imara hutolewa hapa.

Utawala: Njia ya shells Cylindrical kwa Solids ya Mapinduzi kote$x$-axis

Hebu$g(y)$ uendelee na usio na hasi. Kufafanua$Q$ kama kanda imepakana upande wa kulia na grafu ya$g(y)$, upande wa kushoto na$y$ -axis, chini na mstari$y=c$, na juu na mstari$y=d$. Kisha, kiasi cha imara ya mapinduzi yaliyoundwa na$Q$ kuzunguka$x$ -axis hutolewa na

\[V=\int ^d_c(2π\,y\,g(y))\,dy. \nonumber \]

Mfano$\PageIndex{3}$: The Method of Cylindrical Shells for a Solid Revolved around the $x$-axis

Kufafanua$Q$ kama kanda imepakana upande wa kulia na grafu ya$g(y)=2\sqrt{y}$ na upande wa kushoto na$y$ -axis kwa$y∈[0,4]$. Pata kiasi cha imara ya mapinduzi yaliyoundwa na$Q$ yanazunguka$x$ -axis.

Suluhisho

Kwanza, tunahitaji graph kanda$Q$ na imara kuhusishwa ya mapinduzi, kama inavyoonekana katika Kielelezo$\PageIndex{7}$.

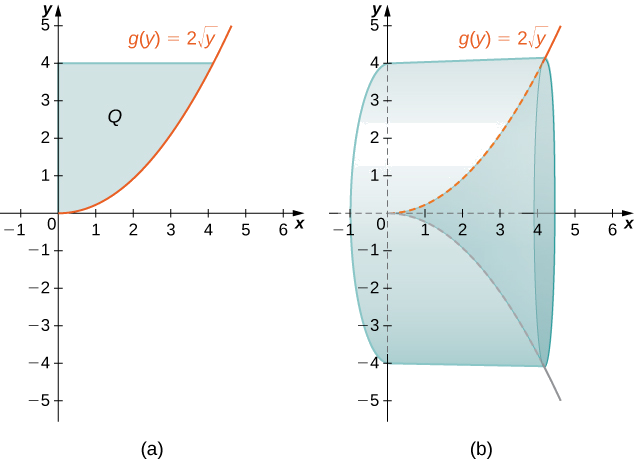
$Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ni safu g (y) =2squareroot (y). Ni Curve kuongezeka katika roboduara ya kwanza kuanzia katika asili. Kati ya mhimili wa y na pembe, kuna eneo la kivuli linaloitwa “Q”. Eneo la kivuli limepakana hapo juu na mstari y=4. Grafu ya pili ni safu sawa katika “a” na iliyoandikwa “b”. Pia ina kanda imara ambayo imeundwa kwa kupokezana pembe katika “a” kuhusu x-axis. Mango huanza kwenye mhimili wa y na huacha saa x=4.$
Kielelezo$\PageIndex{7}$: (a) Kanda$Q$ upande wa kushoto wa kazi$g(y)$ juu ya muda$[0,4]$. (b) imara ya mapinduzi yanayotokana na$Q$ kuzunguka$x$ -axis.

Weka eneo la kivuli$Q$. Kisha kiasi cha imara kinatolewa na

\[ \begin{align*} V =\int ^d_c(2π\,y\,g(y))\,dy \\ =\int ^4_0(2π\,y(2\sqrt{y}))\,dy \\ =4π\int ^4_0y^{3/2}\,dy \\ =4π\left[\dfrac {2y^{5/2}}{5}\right]∣^4_0 \\ =\dfrac {256π}{5}\, \text{units}^3 \end{align*}\]

Zoezi$\PageIndex{3}$

Kufafanua$Q$ kama kanda imepakana upande wa kulia na grafu ya$g(y)=3/y$ na upande wa kushoto na$y$ -axis kwa$y∈[1,3]$. Pata kiasi cha imara ya mapinduzi yaliyoundwa na$Q$ yanazunguka$x$ -axis.

Kidokezo

Tumia mchakato kutoka Mfano$\PageIndex{3}$.

Jibu

$12π$vitengo ³

Kwa mfano unaofuata, tunaangalia imara ya mapinduzi ambayo grafu ya kazi inazunguka mstari mwingine zaidi ya moja ya shoka mbili za kuratibu. Ili kuanzisha hili, tunahitaji kutafakari upya maendeleo ya njia ya shells za cylindrical. Kumbuka kwamba tumegundua kiasi cha moja ya shells kutolewa na

\[\begin{align*} V_{shell} =f(x^∗_i)(π\,x^2_i−π\,x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x^2_i−x^2_{i−1}) \\[4pt] =π\,f(x^∗_i)(x_i+x_{i−1})(x_i−x_{i−1}) \\[4pt] =2π\,f(x^∗_i)\left(\dfrac {x_i+x_{i−1}}{2}\right)(x_i−x_{i−1}).\end{align*}\]

Hii ilikuwa misingi ya shell na Radius nje ya$x_i$ na Radius ndani ya$x_{i−1}$. Ikiwa, hata hivyo, tunazunguka kanda karibu na mstari mwingine zaidi ya$y$ -axis, tuna radius tofauti ya nje na ya ndani. Tuseme, kwa mfano, kwamba sisi mzunguko kanda karibu na mstari$x=−k,$ ambapo$k$ ni baadhi ya mara kwa mara chanya. Kisha, radius ya nje ya shell ni$x_i+k$ na radius ya ndani ya shell ni$x_{i−1}+k$. Kubadilisha maneno haya kwa maneno kwa kiasi, tunaona kwamba wakati mkoa wa ndege unapozunguka karibu na mstari kiasi$x=−k,$ cha shell kinatolewa na

\[\begin{align*} V_{shell} =2π\,f(x^∗_i)(\dfrac {(x_i+k)+(x_{i−1}+k)}{2})((x_i+k)−(x_{i−1}+k)) \\[4pt] =2π\,f(x^∗_i)\left(\left(\dfrac {x_i+x_{i−2}}{2}\right)+k\right)Δx.\end{align*}\]

Kama hapo awali, tunaona kwamba$\dfrac {x_i+x_{i−1}}{2}$ ni midpoint ya muda$[x_{i−1},x_i]$ na inaweza kuwa takriban na$x^∗_i$. Kisha, kiasi cha takriban cha shell ni

\[V_{shell}≈2π(x^∗_i+k)f(x^∗_i)Δx. \nonumber \]

salio ya kuendelea maendeleo kama kabla, na tunaona kwamba

\[V=\int ^b_a(2π(x+k)f(x))dx. \nonumber \]

Tunaweza pia kugeuza kanda karibu na mistari mingine ya usawa au wima, kama vile mstari wa wima katika nusu ya ndege ya haki. Katika kila kesi, formula ya kiasi lazima kubadilishwa ipasavyo. Hasa,$x$ -mrefu katika muhimu lazima kubadilishwa na kujieleza anayewakilisha eneo la shell. Ili kuona jinsi hii inavyofanya kazi, fikiria mfano unaofuata.

Mfano$\PageIndex{4}$: A Region of Revolution Revolved around a Line

Eleza$R$ kama eneo lililofungwa hapo juu na grafu ya$f(x)=x$ na chini na$x$ -axis juu ya muda$[1,2]$. Find kiasi cha imara ya mapinduzi yaliyoundwa na$R$ yanazunguka mstari$x=−1.$

Suluhisho

Kwanza, graph kanda$R$ na imara kuhusishwa ya mapinduzi, kama inavyoonekana katika Kielelezo$\PageIndex{8}$.

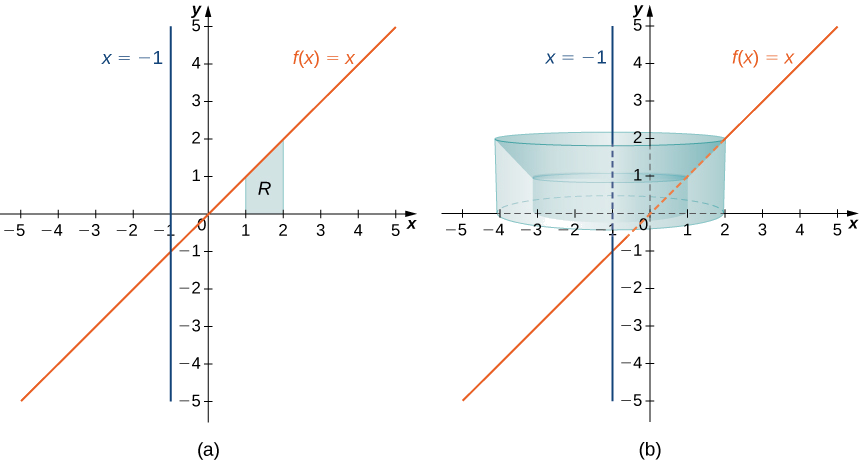
$Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ni mstari f (x) =x, mstari wa diagonal kupitia asili. Kuna eneo la kivuli juu ya mhimili wa x chini ya mstari ulioitwa “R”. Eneo hili limepakana upande wa kushoto na mstari x=1 na kulia kwa mstari x=2. Pia kuna mstari wa wima x=-1 kwenye grafu. Takwimu ya pili ina grafu sawa na “a” na inaitwa “b”. Pia kwenye grafu ni imara iliyoundwa na kupokezana kanda “R” kutoka kwenye grafu ya kwanza kuhusu mstari x=-1.$
Kielelezo$\PageIndex{8}$: (a) Eneo$R$ kati ya grafu ya$f(x)$ na$x$ -axis juu ya muda$[1,2]$. (b) imara ya mapinduzi yanayotokana na$R$ yanazunguka mstari$x=−1.$

Kumbuka kuwa radius ya shell inapewa na$x+1$. Kisha kiasi cha imara kinatolewa na

\[\begin{align*} V =\int ^2_1 2π(x+1)f(x)\, dx \\ =\int ^2_1 2π(x+1)x \, dx=2π\int ^2_1 x^2+x \, dx \\ =2π \left[\dfrac{x^3}{3}+\dfrac{x^2}{2}\right]\bigg|^2_1 \\ =\dfrac{23π}{3} \, \text{units}^3 \end{align*}\]

Zoezi$\PageIndex{4}$

Eleza$R$ kama eneo lililofungwa hapo juu na grafu ya$f(x)=x^2$ na chini na$x$ -axis juu ya muda$[0,1]$. Pata kiasi cha imara ya mapinduzi yaliyoundwa na$R$ yanazunguka mstari$x=−2$.

Kidokezo

Tumia mchakato kutoka Mfano$\PageIndex{4}$.

Jibu

$\dfrac {11π}{6}$vitengo ³

Kwa mfano wetu wa mwisho katika sehemu hii, hebu tuangalie kiasi cha imara ya mapinduzi ambayo kanda ya mapinduzi imefungwa na grafu ya kazi mbili.

Mfano$\PageIndex{5}$: A Region of Revolution Bounded by the Graphs of Two Functions

Eleza$R$ kama eneo lililofungwa hapo juu na grafu ya kazi$f(x)=\sqrt{x}$ na chini na grafu ya kazi$g(x)=1/x$ juu ya muda$[1,4]$. Find kiasi cha imara ya mapinduzi yanayotokana na$R$ yanazunguka$y$ -axis.

Suluhisho

Kwanza, graph kanda$R$ na imara kuhusishwa ya mapinduzi, kama inavyoonekana katika Kielelezo$\PageIndex{9}$.

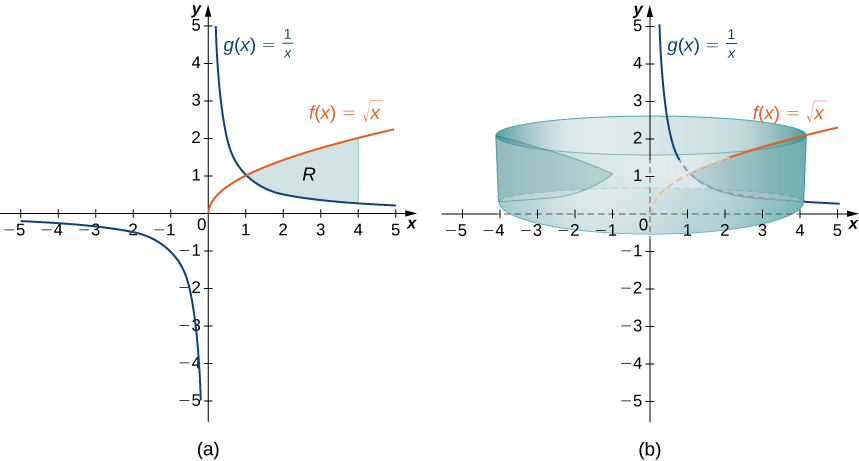
$Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ina curves mbili. Curves ni grafu ya f (x) =squareroot (x) na g (x) =1/x. katika roboduara ya kwanza curves intersect katika (1,1). Kati ya curves katika roboduara ya kwanza kuna kanda kivuli kinachoitwa “R”, imefungwa kwa haki na mstari x=4. Grafu ya pili inaitwa “b” na ni sawa na grafu katika “a”. Pia kwenye grafu hii ni imara ambayo imeundwa kwa kupokezana kanda “R” kutoka kwenye takwimu “a” kuhusu mhimili wa y.$
Kielelezo$\PageIndex{9}$: (a) Eneo$R$ kati ya grafu ya$f(x)$ na grafu ya$g(x)$ zaidi ya muda$[1,4]$. (b) imara ya mapinduzi yanayotokana na$R$ kuzunguka$y$ -axis.

Kumbuka kwamba mhimili wa mapinduzi ni$y$ -axis, hivyo radius ya shell inapewa tu na$x$. Hatuna haja ya kufanya marekebisho yoyote kwa muda x wa integrand yetu. Urefu wa shell, ingawa, hutolewa na$f(x)−g(x)$, hivyo katika kesi hii tunahitaji kurekebisha$f(x)$ muda wa integrand. Kisha kiasi cha imara kinatolewa na

\[\begin{align*} V =\int ^4_1(2π\,x(f(x)−g(x)))\,dx \\[4pt] = \int ^4_1(2π\,x(\sqrt{x}−\dfrac {1}{x}))\,dx=2π\int ^4_1(x^{3/2}−1)dx \\[4pt] = 2π\left[\dfrac {2x^{5/2}}{5}−x\right]\bigg|^4_1=\dfrac {94π}{5} \, \text{units}^3. \end{align*}\]

Zoezi$\PageIndex{5}$

Eleza$R$ kama eneo lililofungwa hapo juu na grafu ya$f(x)=x$ na chini na grafu ya$g(x)=x^2$ zaidi ya muda$[0,1]$. Pata kiasi cha imara ya mapinduzi yaliyoundwa na$R$ yanazunguka$y$ -axis.

Kidokezo

Kidokezo: Tumia mchakato kutoka Mfano$\PageIndex{5}$.

Jibu

$\dfrac {π}{6}$vitengo ³

Njia ipi Tunapaswa kutumia?

Tumejifunza mbinu kadhaa za kutafuta kiasi cha imara ya mapinduzi, lakini tunajuaje njia gani ya kutumia? Mara nyingi huja chini ya uchaguzi ambao muhimu ni rahisi kutathmini. Kielelezo$\PageIndex{10}$ inaeleza mbinu mbalimbali kwa ajili ya yabisi ya mapinduzi kuzunguka$x$ -axis. Ni juu yako kuendeleza meza sawa kwa yabisi ya mapinduzi kuzunguka$y$ -axis.

$Takwimu hii ni meza kulinganisha mbinu tofauti za kutafuta kiasi cha yabisi ya mapinduzi. Nguzo katika meza zimeandikwa “kulinganisha”, “njia ya disk”, “njia ya washer”, na “njia ya shell”. Safu zimeandikwa “formula ya kiasi”, “imara”, “muda wa kugawanya”, “rectangles”, “mkoa wa kawaida”, na “mstatili”. Katika safu ya njia ya disk, formula hutolewa kama muhimu ya uhakika kutoka kwa b ya mara pi [f (x)] ^2. Mango haina cavity katikati, kizigeu ni [a, b], rectangles ni wima, na kanda ya kawaida ni eneo la kivuli juu ya x-axis na chini ya pembe ya f (x). Katika safu ya njia ya washer, formula hutolewa kama muhimu ya uhakika kutoka kwa b ya mara pi [f (x)] ^2- [g (x)] ^2. Mango ina cavity katikati, kizigeu ni [a, b], rectangles ni wima, na mkoa wa kawaida ni eneo la kivuli juu ya pembe ya g (x) na chini ya pembe ya f (x). Katika safu ya njia ya shell, formula hutolewa kama muhimu ya uhakika kutoka c hadi d ya mara 2pi yg (y). Mango ni pamoja na au bila cavity katikati, kizigeu ni [c, d] rectangles ni usawa, na mkoa wa kawaida ni kanda kivuli juu ya x-axis na chini ya Curve ya g (y).$
Kielelezo$\PageIndex{10}$

Hebu tuangalie matatizo kadhaa ya ziada na uamuzi juu ya njia bora ya kuchukua ili kutatua.

Mfano$\PageIndex{6}$: Selecting the Best Method

Kwa kila moja ya matatizo yafuatayo, chagua njia bora ya kupata kiasi cha imara ya mapinduzi yanayotokana na kuzunguka eneo lililopewa karibu na$x$ -axis, na kuanzisha muhimu ili kupata kiasi (usitathmini muhimu).

Mkoa umepakana na grafu ya$y=x, y=2−x,$ na$x$ -axis.

Mkoa umepakana na grafu ya$y=4x−x^2$ na$x$ -axis.

Suluhisho

a.

Kwanza, mchoro kanda na imara ya mapinduzi kama inavyoonekana.

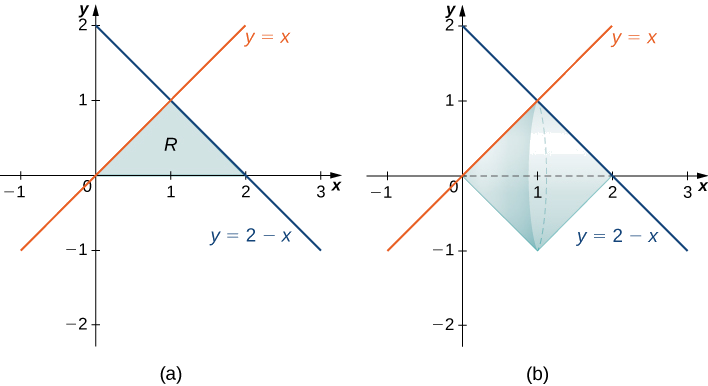
$Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ina mistari miwili y=x na y = 2-x inayotolewa katika roboduara ya kwanza. Mstari huingiliana kwenye (1,1) na kuunda pembetatu juu ya mhimili wa x. Kanda ambayo ni pembetatu ni kivuli. Grafu ya pili inaitwa “b” na ni grafu sawa na “a”. Eneo la pembetatu la kivuli katika “a” limezungushwa karibu na mhimili wa x-ili kuunda imara kwenye grafu ya pili.$
Kielelezo$\PageIndex{11}$: (a) Eneo$R$ limefungwa na mistari miwili na$x$ -axis. (b) Imara ya mapinduzi yanayotokana na yanazunguka$R$ kuhusu$x$ -axis.

Kuangalia kanda, kama tunataka kuunganisha kwa heshima na$x$, tutakuwa na kuvunja muhimu katika vipande viwili, kwa sababu tuna kazi tofauti zinazozuia kanda tena$[0,1]$ na$[1,2]$. Katika kesi hii, kwa kutumia njia ya disk, tungekuwa na

\[V=\int ^1_0 π\,x^2\,dx+\int ^2_1 π(2−x)^2\,dx. \nonumber \]

Kama sisi kutumika mbinu shell badala yake, tunataka kutumia kazi ya y kuwakilisha curves, kuzalisha

\[V=\int ^1_0 2π\,y[(2−y)−y] \,dy=\int ^1_0 2π\,y[2−2y]\,dy. \nonumber \]

Wala wa integrals hizi ni hasa kutaabisha, lakini tangu mbinu shell inahitaji moja tu muhimu, na integrand inahitaji chini kurahisisha, tunapaswa pengine kwenda na njia shell katika kesi hii.

b.

Kwanza, mchoro kanda na imara ya mapinduzi kama inavyoonekana.

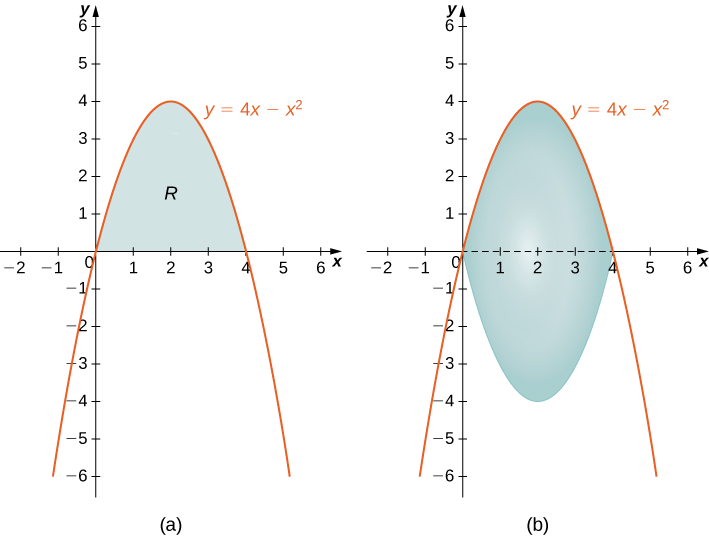
$Takwimu hii ina grafu mbili. Grafu ya kwanza imeandikwa “a” na ni safu y = 4x-x^2. Ni kichwa chini parabola intersecting x-axis katika asili na katika x=4. Eneo lililo juu ya mhimili wa x na chini ya pembe ni kivuli na kinachoitwa “R”. Grafu ya pili iliyoandikwa “b” ni sawa na “a”. Kwenye grafu hii eneo la kivuli “R” limezungushwa karibu na mhimili wa x-ili kuunda imara.$
Kielelezo$\PageIndex{12}$: (a) Kanda$R$ kati ya Curve na$x$ -axis. (b) Imara ya mapinduzi yanayotokana na yanazunguka$R$ kuhusu$x$ -axis.

Kuangalia kanda, itakuwa shida kufafanua mstatili usio na usawa; kanda imefungwa upande wa kushoto na kulia na kazi sawa. Kwa hiyo, tunaweza kumfukuza njia ya shells. Mango haina cavity katikati, hivyo tunaweza kutumia njia ya disks. Kisha

\[V=\int ^4_0π\left(4x−x^2\right)^2\,dx \nonumber \]

Zoezi$\PageIndex{6}$

Chagua njia bora ya kupata kiasi cha imara ya mapinduzi yanayotokana na yanazunguka eneo$x$ lililopewa karibu na mhimili, na kuanzisha muhimu ili kupata kiasi (usitathmini muhimu): eneo lililofungwa na grafu za$y=2−x^2$ na$y=x^2$.

Kidokezo

Mchoro kanda na kutumia Kielelezo$\PageIndex{12}$ kuamua ambayo muhimu ni rahisi kutathmini.

Jibu

Tumia njia ya washers;\[V=\int ^1_{−1}π\left[\left(2−x^2\right)^2−\left(x^2\right)^2\right]\,dx \nonumber \]

Dhana muhimu

Njia ya shells za cylindrical ni njia nyingine ya kutumia muhimu ya uhakika ili kuhesabu kiasi cha imara ya mapinduzi. Njia hii wakati mwingine inafaa kwa njia ya disks au njia ya washers kwa sababu sisi kuunganisha kwa heshima na variable nyingine. Katika hali nyingine, moja muhimu ni ngumu zaidi kuliko nyingine.

Jiometri ya kazi na ugumu wa ushirikiano ni sababu kuu katika kuamua ni njia gani ya ushirikiano wa kutumia.

Mlinganyo muhimu

Njia ya Shells za Cylind

$\displaystyle V=\int ^b_a\left(2π\,x\,f(x)\right)\,dx$

faharasa

njia ya shells za cylind

njia ya kuhesabu kiasi cha imara ya mapinduzi kwa kugawanya imara ndani ya vifuniko vya cylindrical; njia hii ni tofauti na njia za disks au washers kwa kuwa tunaunganisha kwa heshima na kutofautiana kinyume

Kanuni: Njia ya Shells za Cylindrical

Mfano\(\PageIndex{1}\): The Method of Cylindrical Shells I

Zoezi\(\PageIndex{1}\)

Mfano\(\PageIndex{2}\): The Method of Cylindrical Shells II

Zoezi\(\PageIndex{2}\)

Utawala: Njia ya shells Cylindrical kwa Solids ya Mapinduzi kote\(x\)-axis

Mfano\(\PageIndex{3}\): The Method of Cylindrical Shells for a Solid Revolved around the \(x\)-axis

Zoezi\(\PageIndex{3}\)

Mfano\(\PageIndex{4}\): A Region of Revolution Revolved around a Line

Zoezi\(\PageIndex{4}\)

Mfano\(\PageIndex{5}\): A Region of Revolution Bounded by the Graphs of Two Functions

Zoezi\(\PageIndex{5}\)

Mfano\(\PageIndex{6}\): Selecting the Best Method

Zoezi\(\PageIndex{6}\)

Mlinganyo muhimu