6.2: Kuamua Kiasi kwa Slicing

Last updated
Save as PDF

Page ID: 178287

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Kuamua kiasi cha imara kwa kuunganisha sehemu ya msalaba (njia ya slicing).
Pata kiasi cha imara ya mapinduzi kwa kutumia njia ya disk.
Pata kiasi cha imara ya mapinduzi na cavity kwa kutumia njia ya washer.

Katika sehemu iliyotangulia, tulitumia viungo vya uhakika ili kupata eneo kati ya curves mbili. Katika sehemu hii, tunatumia integrals uhakika ili kupata kiasi cha yabisi tatu-dimensional. Tunazingatia mbinu tatu-slicing, disks, na washers-kwa ajili ya kutafuta kiasi hiki, kulingana na sifa za imara.

Volume na Njia ya Slicing

Kama vile eneo ni kipimo cha namba ya kanda mbili-dimensional, kiasi ni kipimo cha namba ya imara tatu-dimensional. Wengi wetu tumehesabu kiasi cha yabisi kwa kutumia kanuni za msingi za kijiometri. Kiasi cha imara ya mstatili, kwa mfano, inaweza kuhesabiwa kwa kuzidisha urefu, upana, na urefu:$V=lwh.$ Fomu kwa kiasi cha:

nyanja

\[V_{sphere}=\dfrac{4}{3}πr^3, \nonumber \]

koni

\[V_{cone}=\dfrac{1}{3}πr^2h \nonumber \]

na piramidi

\[V_{pyramid}=\dfrac{1}{3}Ah \nonumber \]

pia kuletwa. Ingawa baadhi ya fomula hizi zilitokana kwa kutumia jiometri pekee, fomula hizi zote zinaweza kupatikana kwa kutumia ushirikiano.

Tunaweza pia kuhesabu kiasi cha silinda. Ingawa wengi wetu wanafikiria silinda kama kuwa na msingi wa mviringo, kama vile supu inaweza au fimbo ya chuma, katika hisabati neno silinda lina maana ya jumla zaidi. Ili kujadili mitungi katika muktadha huu wa jumla zaidi, tunahitaji kwanza kufafanua msamiati fulani.

Tunafafanua sehemu ya msalaba wa imara kuwa makutano ya ndege na imara. Silinda hufafanuliwa kama imara yoyote ambayo inaweza kuzalishwa kwa kutafsiri mkoa wa ndege pamoja na mstari perpendicular kwa kanda, inayoitwa mhimili wa silinda. Hivyo, sehemu zote za msalaba perpendicular kwa mhimili wa silinda ni sawa. Imara inavyoonekana katika Kielelezo$\PageIndex{1}$ ni mfano wa silinda na msingi noncircular. Ili kuhesabu kiasi cha silinda, basi, tunazidisha eneo la sehemu ya msalaba kwa urefu wa silinda:$V=A⋅h.$ Katika kesi ya silinda ya mviringo sahihi (supu inaweza), hii inakuwa$V=πr^2h.$

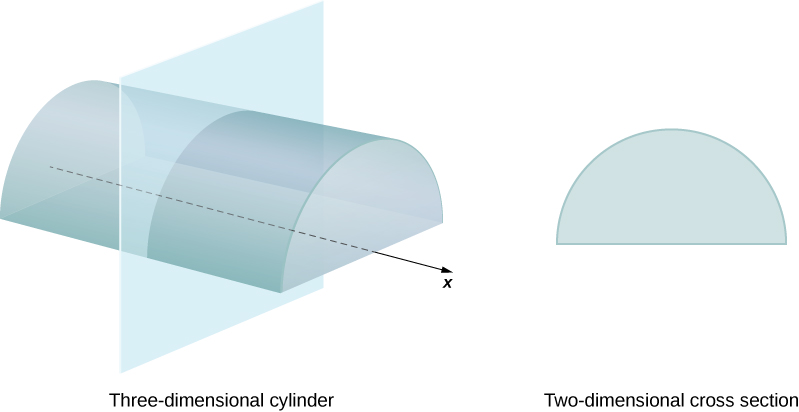
Graphic hii ina takwimu mbili. Takwimu ya kwanza ni nusu ya silinda, kwenye sehemu ya gorofa. Silinda ina mstari kupitia kituo kinachoitwa “x”. Kukata kwa njia ya silinda, perpendicular kwa mstari ni ndege. Takwimu ya pili ni sehemu ya msalaba wa mwelekeo wa silinda inayoingiliana na ndege. Ni mduara wa nusu. — Kielelezo$\PageIndex{1}$*: Kila sehemu ya msalaba wa silinda fulani ni sawa na wengine.*

Ikiwa imara haina sehemu ya msalaba wa mara kwa mara (na sio moja ya yabisi mengine ya msingi), tunaweza kuwa na formula kwa kiasi chake. Katika kesi hii, tunaweza kutumia muhimu ya uhakika ili kuhesabu kiasi cha imara. Tunafanya hivyo kwa kupiga vipande vipande vipande vipande, kukadiria kiasi cha kila kipande, na kisha kuongeza kiasi hicho cha makadirio pamoja. Vipande vinapaswa kuwa sawa na kila mmoja, na tunapoweka vipande vyote pamoja, tunapaswa kupata imara nzima. Fikiria, kwa mfano, S imara inavyoonekana katika Kielelezo$\PageIndex{2}$, kupanua kando ya$x$ -axis.

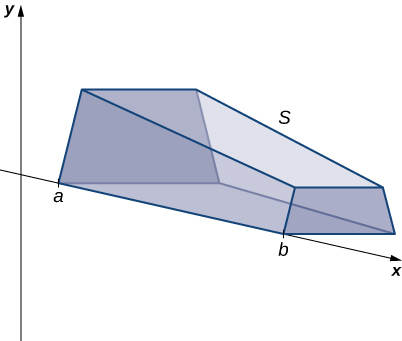
Takwimu hii ni grafu ya imara 3-dimensional. Ina makali moja kando ya x-axis. Mhimili wa x-ni sehemu ya mfumo wa kuratibu wa 2-dimensional na y-axis iliyoandikwa. Makali ya imara kando ya mhimili wa x huanza kwa hatua iliyoandikwa “a” na huacha kwenye hatua iliyoandikwa “b”. — Kielelezo$\PageIndex{2}$: Imara na sehemu tofauti ya msalaba.

Tunataka kugawanywa$S$ katika vipande perpendicular kwa $x$-axis. Kama tunavyoona baadaye katika sura, kunaweza kuwa na nyakati ambapo tunataka kipande imara katika baadhi ya mwelekeo nyingine-kusema, na vipande perpendicular kwa$y$ -axis. Uamuzi wa njia gani ya kukata imara ni muhimu sana. Kama sisi kufanya uchaguzi sahihi, hesabu unaweza kupata messy kabisa. Baadaye katika sura, tunachunguza baadhi ya hali hizi kwa undani na kuangalia jinsi ya kuamua ni njia gani ya kukata imara. Kwa madhumuni ya sehemu hii, hata hivyo, tunatumia vipande perpendicular kwa$x$ -axis.

Kwa sababu eneo msalaba-Sectional si mara kwa mara, sisi basi$A(x)$ kuwakilisha eneo la sehemu ya msalaba katika hatua x Sasa hebu$P={x_0,x_1…,X_n}$ kuwa kizigeu mara kwa mara ya$[a,b]$, na kwa$i=1,2,…n$, basi$S_i$ kuwakilisha kipande cha$S$ kunyoosha kutoka$x_{i−1}$ kwa$x_i$. Takwimu inayofuata inaonyesha imara iliyokatwa na$n=3$.

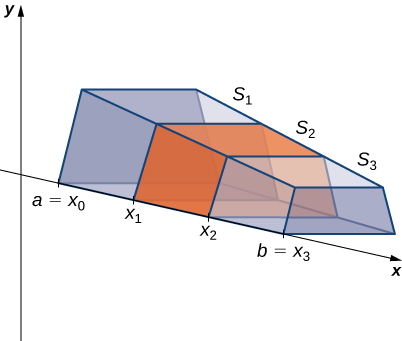
Hatimaye, kwa$i=1,2,…n,$ hebu$x^∗_i$ kuwa hatua holela katika$[x_{i−1},x_i]$. Kisha kiasi cha kipande$S_i$ kinaweza kuhesabiwa na$V(S_i)≈A(x^∗_i)\,Δx$. Kuongeza makadirio haya pamoja, tunaona kiasi cha imara nzima$S$ inaweza kuwa approximated na

\[V(S)≈\sum_{i=1}^nA(x^∗_i)\,Δx. \nonumber \]

Kwa sasa, tunaweza kutambua hii kama jumla Riemann, na hatua yetu ya pili ni kuchukua kikomo kama$n→∞.$ Kisha tuna

\[V(S)=\lim_{n→∞}\sum_{i=1}^nA(x^∗_i)\,Δx=∫_a^b A(x)\,dx. \nonumber \]

Mbinu tuliyoelezea tu inaitwa njia ya slicing. Ili kuitumia, tunatumia mkakati wafuatayo.

Mkakati wa Kutatua Matatizo: Kutafuta Kiasi kwa Njia ya Slicing

Kuchunguza imara na kuamua sura ya sehemu ya msalaba wa imara. Mara nyingi husaidia kuteka picha ikiwa moja haitolewa.
Tambua formula kwa eneo la sehemu ya msalaba.
Unganisha fomu ya eneo juu ya muda unaofaa ili kupata kiasi.

Kumbuka kwamba katika sehemu hii, tunadhani vipande ni perpendicular kwa$x$ -axis. Kwa hiyo, formula ya eneo ni katika suala la x na mipaka ya ushirikiano uongo juu ya $x$-axis. Hata hivyo, mkakati wa kutatua matatizo umeonyeshwa hapa ni halali bila kujali jinsi tunavyochagua kipande kilicho imara.

Mfano$\PageIndex{1}$: Deriving the Formula for the Volume of a Pyramid

Tunajua kutoka jiometri kwamba formula ya kiasi cha piramidi ni$V=\dfrac{1}{3}Ah$. Ikiwa piramidi ina msingi wa mraba$V=\dfrac{1}{3}a^2h$, hii inakuwa, ambapo inaashiria urefu wa upande mmoja wa msingi. Sisi ni kwenda kutumia njia slicing kupata formula hii.

Suluhisho

Tunataka kutumia njia ya slicing kwa piramidi na msingi wa mraba. Ili kuanzisha muhimu, fikiria piramidi iliyoonyeshwa kwenye Kielelezo$\PageIndex{4}$, iliyoelekezwa kando ya $x$mhimili.

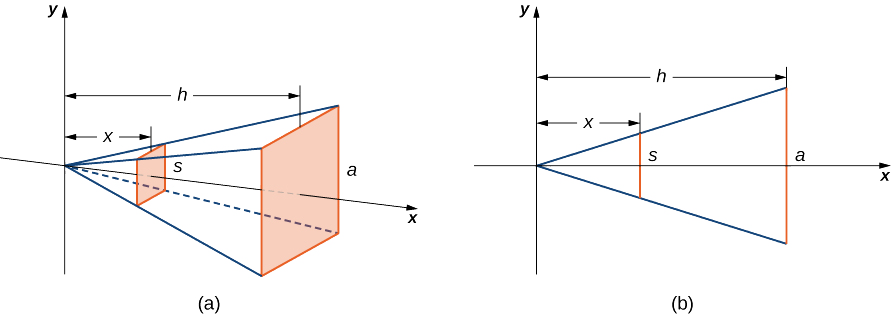
Takwimu hii ina grafu mbili. Grafu ya kwanza, iliyoitwa “a”, ni piramidi upande wake. Mhimili wa x hupitia katikati ya piramidi. Hatua ya juu ya piramidi ni asili ya mfumo wa kuratibu x y. Msingi wa piramidi ni kivuli na kinachoitwa “a”. Ndani ya piramidi ni mstatili wa kivuli kinachoitwa “s”. Umbali kutoka kwa mhimili wa y hadi msingi wa piramidi ni kinachoitwa “h”. umbali mstatili ndani ya piramidi kwa y axis ni kinachoitwa “x”. Takwimu ya pili ni sehemu ya msalaba wa piramidi na shaba za x na y zilizoandikwa. Sehemu ya msalaba ni pembetatu na upande mmoja unaoitwa “a”, perpendicular kwa x-axis. Umbali a ni kutoka kwa mhimili wa y ni h.Kuna mstari mwingine wa perpendicular kwa x-axis ndani ya pembetatu. Ni kinachoitwa “s”. Ni vitengo x kutoka kwa mhimili wa y. — Kielelezo$\PageIndex{4}$: (a) Piramidi yenye msingi wa mraba inaelekezwa kando ya$x$ mhimili. (b) Mtazamo wa pande mbili wa piramidi unaonekana kutoka upande.

Sisi kwanza tunataka kuamua sura ya sehemu ya msalaba wa piramidi. Tunajua msingi ni mraba, hivyo sehemu za msalaba ni mraba pia (hatua ya 1). Sasa tunataka kuamua formula kwa eneo la moja ya viwanja hivi vya msalaba. Kuangalia Kielelezo$\PageIndex{4}$ (b), na kutumia uwiano, kwa kuwa hizi ni pembetatu sawa, tuna

\[\dfrac{s}{a}=\dfrac{x}{h} \nonumber \]

\[s=\dfrac{ax}{h}. \nonumber \]

Kwa hiyo, eneo la moja ya mraba msalaba ni

\[A(x)=s^2=\left(\dfrac{ax}{h}\right)^2 \quad\quad\text{(step 2)} \nonumber \]

Kisha tunapata kiasi cha piramidi kwa kuunganisha kutoka$0$ kwa$h$ (hatua ya 3):

\[V=∫_0^hA(x)\,dx=∫_0^h\left(\dfrac{ax}{h}\right)^2\,dx=\dfrac{a^2}{h^2}∫_0^hx^2\,dx=\left.\Big[\dfrac{a^2}{h^2}\left(\dfrac{1}{3}x^3\right)\Big]\right|^h_0=\dfrac{1}{3}a^2h. \nonumber \]

Hii ni formula tulikuwa tukiangalia.

Zoezi$\PageIndex{1}$

Tumia njia ya slicing ili kupata formula\[V=\dfrac{1}{3}πr^2h \nonumber \] kwa kiasi cha koni ya mviringo.

Kidokezo: Tumia pembetatu sawa, kama katika Mfano$\PageIndex{1}$.

Yabisi ya Mapinduzi

Ikiwa eneo katika ndege linazunguka mstari katika ndege hiyo, imara inayoitwa imara ya mapinduzi, kama inavyoonekana katika takwimu ifuatayo.

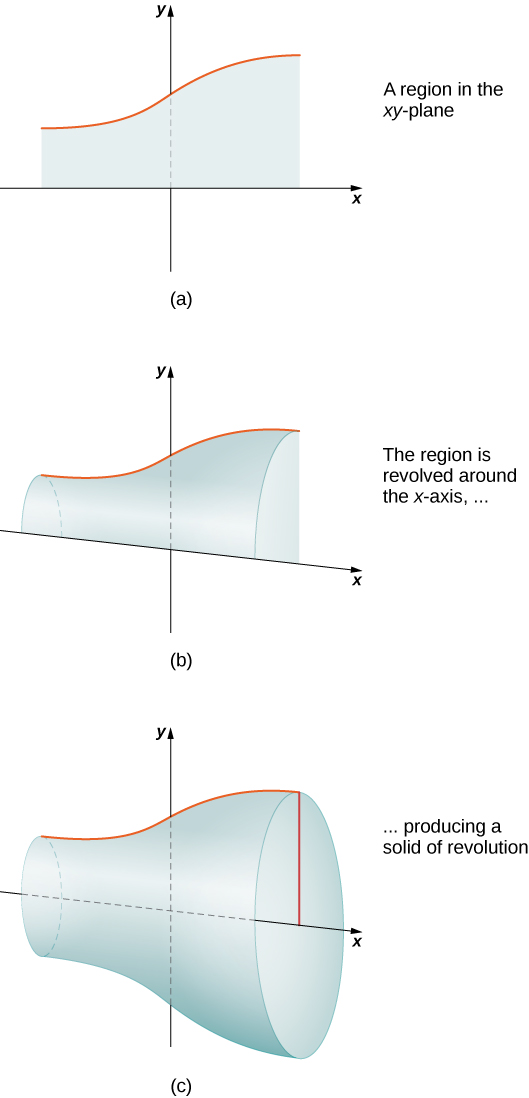
Takwimu hii ina grafu tatu. Grafu ya kwanza, iliyoitwa “a” ni kanda katika ndege ya x y. Kanda huundwa na pembe juu ya mhimili wa x-na mhimili wa x-. Grafu ya pili, iliyoitwa “b” ni kanda sawa na katika “a”, lakini inaonyesha eneo linaloanza kuzunguka karibu na mhimili wa x. Grafu ya tatu, iliyoitwa “c” ni imara iliyoundwa na kupokezana kanda kutoka “a” kabisa karibu na x-axis, kutengeneza imara. — Kielelezo$\PageIndex{5}$: (a) Hii ni eneo ambalo linazunguka$x$ -axis. (b) Kama eneo linaanza kuzunguka mhimili, linafuta imara ya mapinduzi. (c) Hii ni imara inayosababisha wakati mapinduzi yamekamilika.

Yabisi ya mapinduzi ni ya kawaida katika maombi ya mitambo, kama vile sehemu za mashine zinazozalishwa na lathe. Tunatumia sehemu hii yote kuangalia yabisi ya aina hii. Mfano unaofuata unatumia njia ya slicing kuhesabu kiasi cha imara ya mapinduzi.

Mfano$\PageIndex{2}$: Using the Slicing Method to find the Volume of a Solid of Revolution

Kutumia njia slicing kupata kiasi cha imara ya mapinduzi imepakana na grafu ya$f(x)=x^2−4x+5,x=1$,$x=4,$ na kuzungushwa kuhusu$x$ -axis.

Suluhisho

Kutumia mkakati wa kutatua matatizo, sisi kwanza mchoro grafu ya kazi quadratic juu ya muda$[1,4]$ kama inavyoonekana katika takwimu zifuatazo.

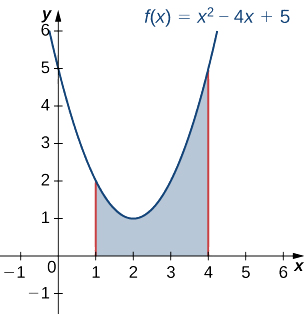
Takwimu hii ni grafu ya parabola f (x) =x ^ 2-4x+5. Parabola ni juu ya eneo la kivuli juu ya x-axis. Mkoa umepakana upande wa kushoto na mstari katika x=1 na kulia kwa mstari katika x=4. — Kielelezo$\PageIndex{6}$: mkoa kutumika kuzalisha imara ya mapinduzi.

Kisha, zunguka kanda karibu na$x$ -axis, kama inavyoonekana katika takwimu ifuatayo.

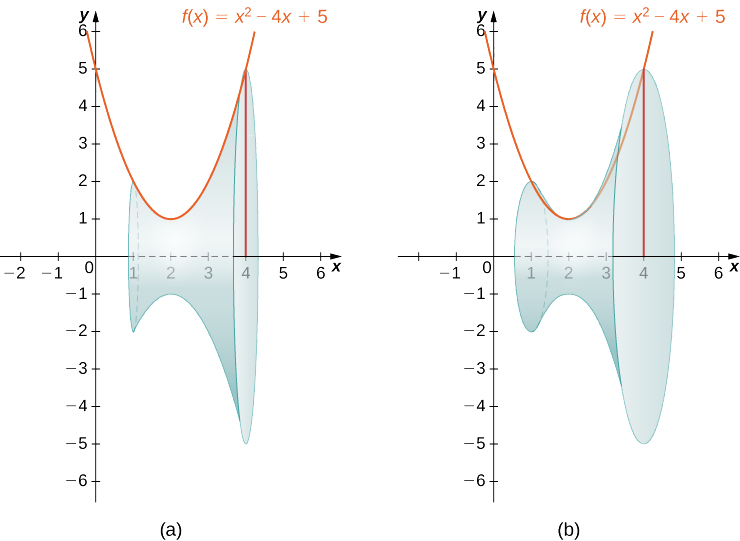
Takwimu hii ina grafu mbili za parabola f (x) =x ^ 2-4x+5. Parabola ni juu ya eneo la kivuli juu ya x-axis. Mkoa umepakana upande wa kushoto na mstari katika x=1 na kulia kwa mstari katika x=4. Grafu ya kwanza ina imara ya kivuli chini ya parabola. Mango hii imeundwa kwa kupokezana parabola karibu na mhimili wa x. Grafu ya pili ni sawa na ya kwanza, na imara ikizungushwa ili kuonyesha imara. — Kielelezo$\PageIndex{7}$: Maoni mawili, (a) na (b), ya imara ya mapinduzi zinazozalishwa na yanazunguka kanda katika Kielelezo$\PageIndex{6}$ kuhusu$x$ **-axis.**

Kwa kuwa imara iliundwa na kuzunguka kanda karibu na$x$ -axis, sehemu za msalaba ni miduara (hatua ya 1). Eneo la sehemu ya msalaba, basi, ni eneo la mduara, na radius ya mduara hutolewa na$f(x).$ Tumia formula kwa eneo la mduara:

\[A(x)=πr^2=π[f(x)]^2=π(x^2−4x+5)^2\quad\quad\text{(step 2).} \nonumber \]

Kiasi, basi, ni (hatua ya 3)

\[\begin{align*} V &=∫_a^b A(x)\,dx \\ &=∫^4_1π(x^2−4x+5)^2\,dx \\ &=π∫^4_1(x^4−8x^3+26x^2−40x+25)\,dx \\ &=\left. π\left(\dfrac{x^5}{5}−2x^4+\dfrac{26x^3}{3}−20x^2+25x\right)\right|^4_1 \\ &=\dfrac{78}{5}π \end{align*}\]

Kiasi ni$78π/5\,\text{units}^3.$

Zoezi$\PageIndex{2}$

Tumia njia ya slicing ili kupata kiasi cha imara ya mapinduzi yaliyoundwa na kuzunguka kanda kati ya grafu ya kazi$f(x)=1/x$ na$x$ -axis juu ya muda$[1,2]$ karibu na$x$ -axis. Angalia takwimu ifuatayo.

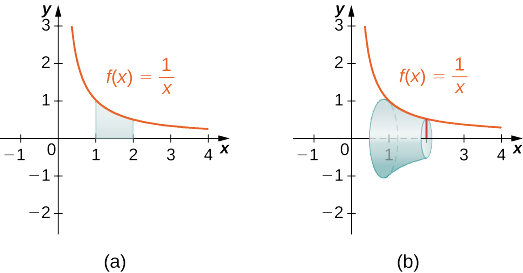
$Takwimu hii ina grafu mbili. Grafu ya kwanza ni Curve f (x) =1/x Ni curve kupungua, juu ya x-axis katika roboduara ya kwanza. Grafu ina eneo la kivuli chini ya pembe kati ya x=1 na x=2. Grafu ya pili ni safu f (x) =1/x katika roboduara ya kwanza. Pia, chini ya grafu hii, kuna imara kati ya x=1 na x=2 ambayo imeundwa kwa kupokezana kanda kutoka grafu ya kwanza karibu na x-axis.$

Kidokezo: Tumia mkakati wa kutatua matatizo uliowasilishwa mapema na ufuate Mfano$\PageIndex{2}$ ili kusaidia na hatua ya 2.

Jibu: $\dfrac{π}{2} \,\text{units}^3$

Njia ya Disk

Wakati sisi kutumia mbinu slicing na yabisi ya mapinduzi, mara nyingi huitwa njia disk kwa sababu, kwa yabisi ya mapinduzi, vipande kutumika juu ya takriban kiasi cha imara ni disks. Ili kuona hili, fikiria imara ya mapinduzi yanayotokana na kuzunguka kanda kati ya grafu ya kazi$f(x)=(x−1)^2+1$ na $x$-axis juu ya muda$[−1,3]$ karibu na$x$ -axis. Grafu ya kazi na disk mwakilishi huonyeshwa kwenye Mchoro$\PageIndex{8}$ (a) na (b). Mkoa wa mapinduzi na imara inayoonekana huonyeshwa kwenye Kielelezo$\PageIndex{8}$ (c) na (d).

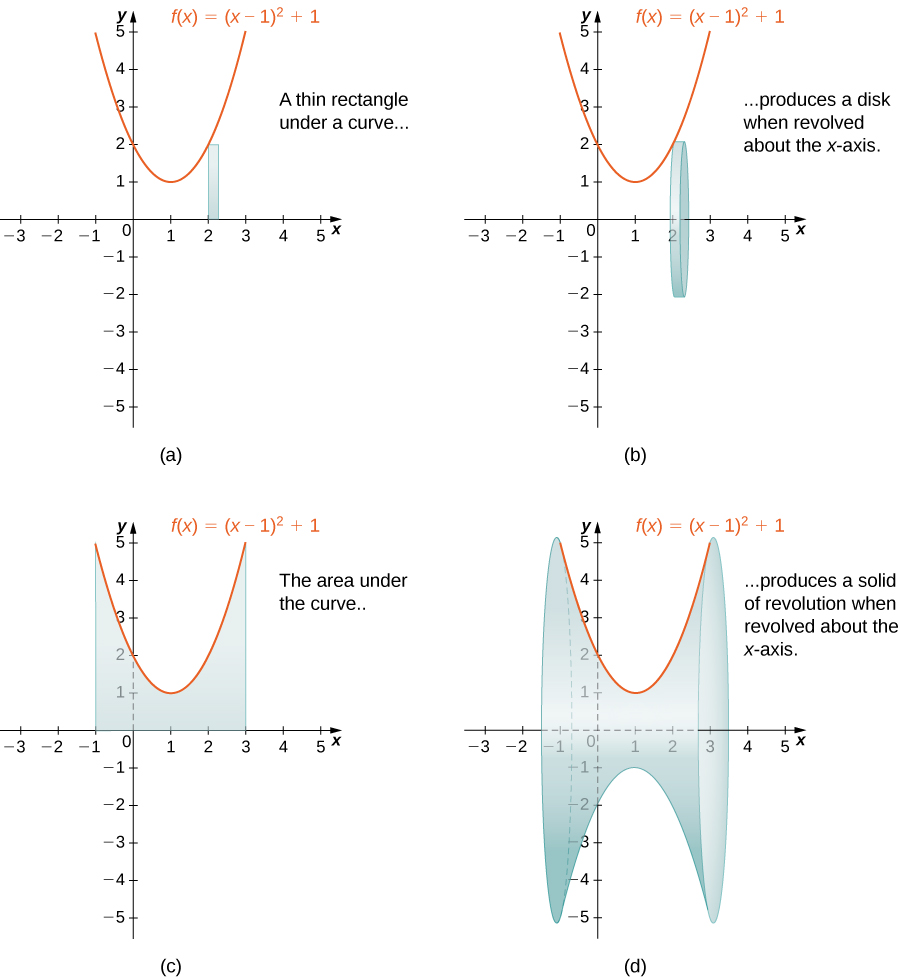
Takwimu hii ina grafu nne. Grafu ya kwanza, iliyoandikwa “a” ni parabola f (x) = (x-1) ^2+1. Curve iko juu ya mhimili wa x na huingilia mhimili wa y katika y=2. Chini ya pembe katika roboduara ya kwanza ni mstatili wa wima unaoanzia kwenye mhimili wa x na kuacha kwenye pembe. Grafu ya pili, iliyoandikwa “b” ni parabola sawa na katika grafu ya kwanza. Mstatili chini ya parabola kutoka kwenye grafu ya kwanza imezungushwa karibu na x-axis kutengeneza diski imara. Grafu ya tatu iliyoitwa “c” ni parabola sawa na grafu ya kwanza. Kuna eneo la kivuli lililofungwa hapo juu na parabola, upande wa kushoto na mstari x=-1 na kulia kwa mstari x=3, na chini na x-axis. Grafu ya nne iliyoitwa “d” ni parabola sawa na grafu ya kwanza. Eneo kutoka kwenye grafu ya tatu limezunguka mhimili wa x-axis ili kuunda imara. — Kielelezo$\PageIndex{8}$: (a) Mstatili mwembamba wa kukadiria eneo chini ya pembe. (b) Disk mwakilishi iliyoundwa na kugeuka mstatili kuhusu$x$ **-axis.** (c) Eneo chini ya pembe linahusu$x$ **-axis,** na kusababisha (d) imara ya mapinduzi.

Kielelezo$\PageIndex{8}$: (e) toleo nguvu ya hii imara ya mapinduzi yanayotokana kwa kutumia CalcPlot3D.

Tayari kutumika rasmi Riemann jumla ya maendeleo ya formula kiasi wakati sisi maendeleo njia slicing. Tunajua kwamba\[∫_a^b A(x)\,dx.\nonumber \]

Tofauti pekee na njia ya disk ni kwamba tunajua formula kwa eneo la msalaba kabla ya muda; ni eneo la mduara. Hii inatoa utawala wafuatayo.

Njia ya Disk

Hebu$f(x)$ uendelee na usio na hasi. Kufafanua$R$ kama kanda imepakana juu na grafu ya$f(x)$, chini na$x$ -axis, upande wa kushoto na mstari$x=a$, na upande wa kulia na mstari$x=b$. Kisha, kiasi cha imara ya mapinduzi yaliyoundwa na$R$ kuzunguka$x$ -axis hutolewa na

\[V=∫^b_aπ[f(x)]^2\,dx. \nonumber \]

Kiasi cha imara tumekuwa tukijifunza (Kielelezo$\PageIndex{8}$) kinatolewa na

\ [kuanza {align*} V &=^b_aπ\ kushoto [f (x)\ kulia] ^2\, dx\\
&=^3_ {,11} π\ kubwa [(x,1-1) ^2+1\ kubwa] ^2\, dx=π^3_ {-1}\ kubwa [(x-1) ^4+2 (x-1) ^2+1 ^2+1\ big] ^2\, dx\\
&=π\ kushoto. \ Big [\ frac {1} {5} (x-1) ^5+\ Frac {2} {3} (x-1) ^3+x\ Big]\ haki|^3_ {-1}\\
&=π\ kushoto [\ frac {32} {5} +\ Frac {16} {3} +3\ haki) -\ kushoto (\Frac {32} {5} {16} {3} +3\ haki) -\ kushoto (\Frac {32} {5} {16} {3} +3\ haki) -\ kushoto (\Frac {32} {5} {16} {3} +32} {5} -\ frac {16} {3} -1\ haki)\ haki]\\
&=\ frac {412π} {15}\,\ maandishi {vitengo} ^3. \ mwisho {align*}\]

Hebu tuangalie mifano fulani.

Mfano$\PageIndex{3}$: Using the Disk Method to Find the Volume of a Solid of Revolution 1

Tumia njia ya disk ili kupata kiasi cha imara ya mapinduzi yanayotokana na kupokezana kanda kati ya grafu ya$f(x)=\sqrt{x}$ na$x$ -axis juu ya muda$[1,4]$ karibu na$x$ -axis.

Suluhisho

Grafu za kazi na imara ya mapinduzi zinaonyeshwa katika takwimu ifuatayo.

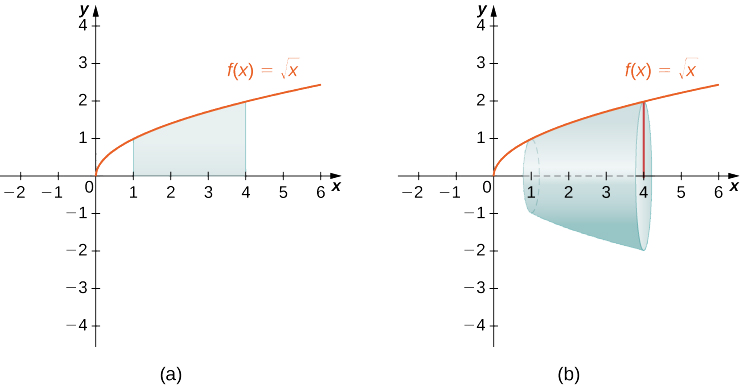
Takwimu hii ina grafu mbili. Grafu ya kwanza iliyoandikwa “a” ni safu f (x) = mraba (x). Ni safu inayoongezeka juu ya mhimili wa x. Curve iko katika roboduara ya kwanza. Chini ya pembe ni eneo lililofungwa na x=1 na x=4. Chini ya kanda ni x-axis. Grafu ya pili iliyoandikwa “b” ni safu sawa na grafu ya kwanza. Eneo imara kutoka kwenye grafu ya kwanza limezungushwa karibu na mhimili wa x-ili kuunda kanda imara. — Kielelezo$\PageIndex{9}$: (a) Kazi$f(x)=\sqrt{x}$ juu ya muda$[1,4]$. (b) imara ya mapinduzi iliyopatikana kwa kuzunguka kanda chini ya grafu ya$f(x)$ juu$x$ **-axis**.

Tuna

\ [kuanza {align*} v&=^B_Aπ\ kubwa [f (x)\ kubwa] ^2\, dx\\
&=^4_1π\ kushoto [\ sqrt {x}\ haki] ^2\, dx=π^4_1x\, dx\\ &=\ dfrac {π} {2} x ^ 2\ big|^ 4_1x\, dx\\
&=\ dfrac {π} {2} x ^ 2\ big|^ 4_1x\ _1=\ dfrac {15π} {2}\ mwisho {align*}\]

Kiasi ni$(15π)/2 \,\text{units}^3.$

Zoezi$\PageIndex{3}$

Tumia njia ya disk ili kupata kiasi cha imara ya mapinduzi yanayotokana na kupokezana kanda kati ya grafu ya$f(x)=\sqrt{4−x}$ na$x$ -axis juu ya muda$[0,4]$ karibu na$x$ -axis.

Kidokezo: Tumia utaratibu kutoka kwa Mfano$\PageIndex{3}$.

Jibu: $8π \,\text{units}^3$

Hadi sasa, mifano yetu ina mikoa yote inayohusika ilizunguka$x$ -axis, lakini tunaweza kuzalisha imara ya mapinduzi kwa kuzunguka eneo la ndege karibu na mstari wowote wa usawa au wima. Katika mfano unaofuata, tunaangalia imara ya mapinduzi ambayo yamezalishwa na kuzunguka eneo karibu na$y$ -axis. Mitambo ya njia ya disk ni sawa na wakati$x$ -axis ni mhimili wa mapinduzi, lakini tunaelezea kazi kwa suala la$y$ na tunaunganisha kwa heshima na y pia. Hii ni muhtasari katika sheria ifuatayo.

Utawala: Method Disk kwa Solids ya Mapinduzi kote$y$-axis

Hebu$g(y)$ uendelee na usio na hasi. Kufafanua$Q$ kama kanda imepakana upande wa kulia na grafu ya$g(y)$, upande wa kushoto na$y$ -axis, chini na mstari$y=c$, na juu na mstari$y=d$. Kisha, kiasi cha imara ya mapinduzi yaliyoundwa na$Q$ kuzunguka$y$ -axis hutolewa na

\[V=∫^d_cπ\big[g(y)\big]^2\,dy. \nonumber \]

Mfano unaofuata unaonyesha jinsi sheria hii inafanya kazi katika mazoezi.

Mfano$\PageIndex{4}$: Using the Disk Method to Find the Volume of a Solid of Revolution 2

Hebu$R$ kuwa kanda imefungwa na grafu ya$g(y)=\sqrt{4−y}$ na$y$ -axis juu ya muda$y$ -axis$[0,4]$. Tumia njia ya disk ili kupata kiasi cha imara ya mapinduzi yanayotokana na kupokezana$R$ karibu na$y$ -axis.

Suluhisho

Kielelezo$\PageIndex{10}$ kinaonyesha kazi na disk mwakilishi ambayo inaweza kutumika kukadiria kiasi. Angalia kwamba kwa kuwa tunazunguka kazi karibu na$y$ -axis, disks ni za usawa, badala ya wima.

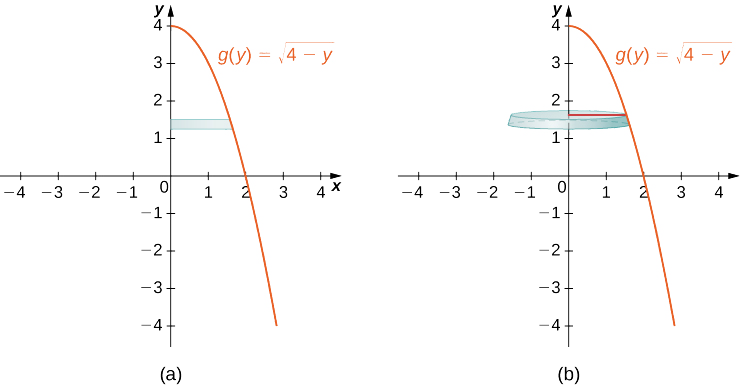
Takwimu hii ina grafu mbili. Grafu ya kwanza iliyoandikwa “a” ni safu g (y) = mraba (4-y). Ni curve kupungua kuanzia kwenye mhimili y saa y = 4. Kati ya pembe na mhimili wa y ni mstatili usio na usawa. Mstatili huanza kwenye mhimili wa y na huacha kwenye pembe. Grafu ya pili iliyoandikwa “b” ni safu sawa na grafu ya kwanza. Mstatili kutoka kwenye grafu ya kwanza umezungushwa karibu na mhimili wa y ili kuunda disk ya usawa. — Kielelezo$\PageIndex{10}$: (a) Inaonyeshwa ni mstatili mwembamba kati ya pembe ya kazi$g(y)=\sqrt{4−y}$ na$y$ **-axis.** (b) Mstatili huunda disk mwakilishi baada ya mapinduzi kuzunguka$y$ **-axis.**

Kanda ya kuwa revolved na imara kamili ya mapinduzi ni taswira katika takwimu zifuatazo.

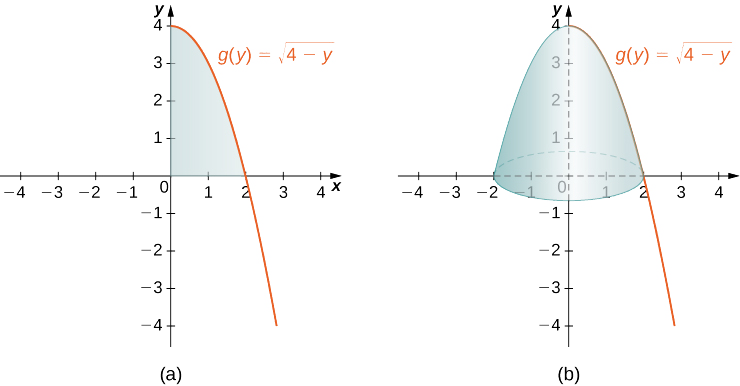
Takwimu hii ina grafu mbili. Grafu ya kwanza iliyoandikwa “a” ni safu g (y) = mraba (4-y). Ni curve kupungua kuanzia kwenye mhimili y saa y = 4. Kanda iliyoundwa na x-axis, y-axis, na curve ni kivuli. Mkoa huu uko katika roboduara ya kwanza. Grafu ya pili iliyoandikwa “b” ni safu sawa na grafu ya kwanza. Eneo kutoka kwenye grafu ya kwanza limezungushwa karibu na mhimili wa y ili kuunda imara. — Kielelezo$\PageIndex{11}$: (a) Eneo upande wa kushoto wa kazi$g(y)=\sqrt{4−y}$ juu ya muda wa$y$ -axis$[0,4]$. (b) Imara ya mapinduzi yaliyoundwa na kuzunguka kanda kuhusu$y$ -axis.

Ili kupata kiasi, tunaunganisha kwa heshima$y$. Tunapata

\[V=∫^d_cπ\big[g(y)\big]^2\,dy=∫^4_0π\left[\sqrt{4−y}\right]^2\,dy=π∫^4_0(4−y)\,dy=π\left.\left[4y−\frac{y^2}{2}\right]\right|^4_0=8π. \nonumber \]

Kiasi ni$8π \,\text{units}^3$.

Zoezi$\PageIndex{4}$

Tumia njia ya disk ili kupata kiasi cha imara ya mapinduzi yanayotokana na kupokezana kanda kati ya grafu ya$g(y)=y$ na$y$ -axis juu ya muda$[1,4]$ karibu na$y$ -axis.

Kidokezo: Tumia utaratibu kutoka kwa Mfano$\PageIndex{4}$.

Jibu: $21π \,\text{units}^3$

Njia ya Washer

Baadhi ya yabisi ya mapinduzi yana mashimo katikati; si imara njia yote hadi mhimili wa mapinduzi. Wakati mwingine, hii ni matokeo tu ya jinsi eneo la mapinduzi linavyoumbwa kwa heshima na mhimili wa mapinduzi. Katika hali nyingine, cavities hutokea wakati mkoa wa mapinduzi hufafanuliwa kama kanda kati ya grafu ya kazi mbili. Njia ya tatu hii inaweza kutokea ni pale mhimili wa mapinduzi zaidi ya $x$-axis au $y$-axis unachaguliwa.

Wakati imara ya mapinduzi ina cavity katikati, vipande vinavyotumiwa kufikia kiasi sio disks, lakini washers (disks na mashimo katikati). Kwa mfano, fikiria eneo lililofungwa hapo juu na grafu ya kazi$f(x)=\sqrt{x}$ na chini na grafu ya kazi$g(x)=1$ zaidi ya muda$[1,4]$. Wakati mkoa huu unazunguka$x$ -axis, matokeo yake ni imara na cavity katikati, na vipande ni washers. Grafu ya kazi na washer mwakilishi huonyeshwa kwenye Mchoro$\PageIndex{12}$ (a) na (b). Mkoa wa mapinduzi na imara inayoonekana huonyeshwa kwenye Kielelezo$\PageIndex{12}$ (c) na (d).

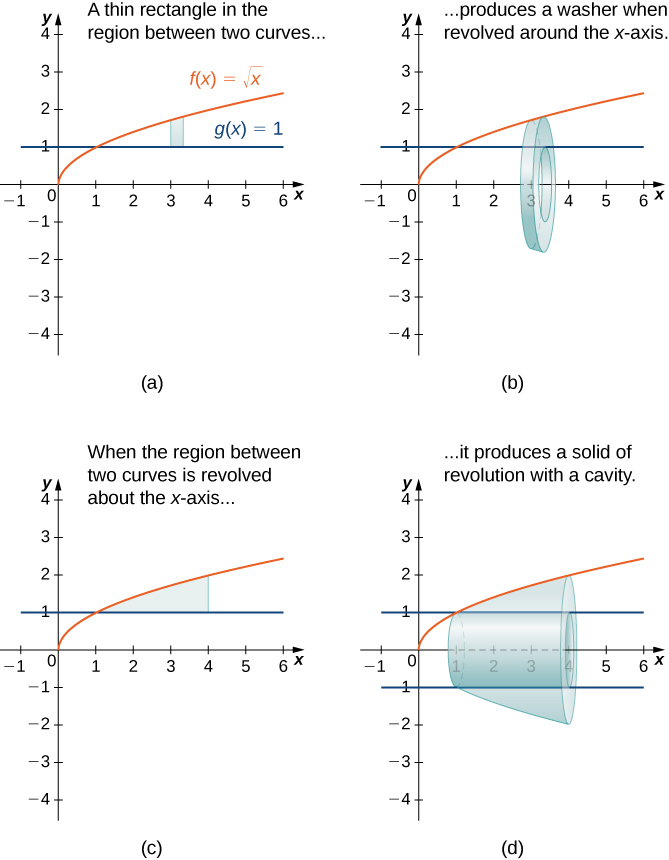
Takwimu hii ina grafu nne. Grafu ya kwanza inaitwa “a” na ina kazi mbili f (x) =squareroot (x) na g (x) =1 iliyopigwa katika quadrant ya kwanza. f (x) ni safu inayoongezeka kuanzia asili na g (x) ni mstari wa usawa saa y = 1. Curves intersect katika jozi kuamuru (1,1). Kati ya curves ni mstatili kivuli na chini juu ya g (x) na juu katika f (x). Grafu ya pili iliyoandikwa “b” ni sawa na safu mbili kama grafu ya kwanza. Mstatili wa kivuli kati ya curves kutoka grafu ya kwanza umezungushwa karibu na mhimili wa x ili kuunda disk wazi au washer. Grafu ya tatu iliyoitwa “a” ina curves mbili sawa na grafu ya kwanza. Kuna kanda kivuli kati ya curves mbili kati ya ambapo wao intersect na mstari katika x = 4. Grafu ya nne ni sawa na curves mbili kama ya kwanza na kanda kutoka grafu ya tatu kuzungushwa karibu na x-axis kutengeneza kanda imara na kituo cha mashimo. Kituo cha mashimo kinawakilishwa kwenye grafu na mistari iliyovunjika ya usawa saa y=1 na y=-1. — Kielelezo$\PageIndex{12}$: (a) Mstatili mwembamba katika kanda kati ya curves mbili. (b) Disk mwakilishi iliyoundwa na kugeuka mstatili kuhusu$x$ **-axis.** (c) kanda kati ya curves juu ya muda fulani. (d) kusababisha imara ya mapinduzi.

Kielelezo$\PageIndex{12}$: (e) toleo nguvu ya hii imara ya mapinduzi yanayotokana kwa kutumia CalcPlot3D.

Eneo la msalaba, basi, ni eneo la mduara wa nje chini ya eneo la mduara wa ndani. Katika kesi hiyo,

$A(x)=π\left(\sqrt{x}\right)^2−π(1)^2=π(x−1).$

Kisha kiasi cha imara ni

\[V=∫^b_a A(x)\,dx=∫^4_1π(x−1)\,dx=π\left.\left[\frac{x^2}{2}−x\right]\right|^4_1=\frac{9}{2}π\,\text{units}^3. \nonumber \]

Kuzalisha mchakato huu hutoa njia ya washer.

Kanuni: Njia ya Washer

Tuseme$f(x)$ na$g(x)$ ni kuendelea, kazi zisizo na hasi kama hiyo$f(x)≥g(x)$ juu$[a,b]$. Hebu$R$ kuashiria eneo lililofungwa hapo juu na grafu ya$f(x)$, chini na grafu ya$g(x)$, upande wa kushoto na mstari$x=a$, na upande wa kulia na mstari$x=b$. Kisha, kiasi cha imara ya mapinduzi yaliyoundwa na$R$ kuzunguka$x$ -axis hutolewa na

\[V=∫^b_aπ\left[(f(x))^2−(g(x))^2\right]\,dx. \nonumber \]

Mfano$\PageIndex{5}$: Using the Washer Method

Kupata kiasi cha imara ya mapinduzi sumu na yanazunguka eneo imepakana juu na grafu ya$f(x)=x$ na chini na grafu ya$g(x)=1/x$ zaidi ya muda$[1,4]$ karibu$x$ -axis.

Suluhisho

Grafu za kazi na imara ya mapinduzi zinaonyeshwa katika takwimu ifuatayo.

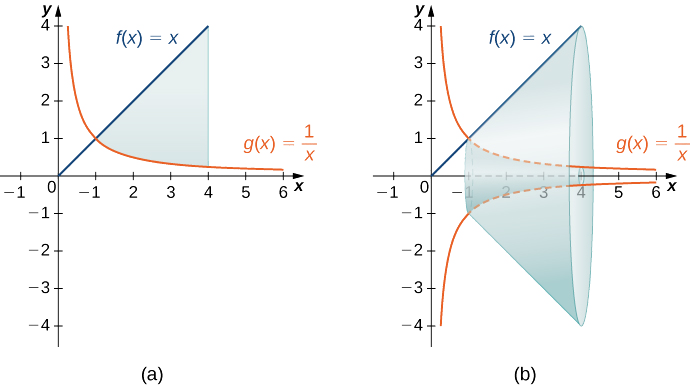
Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ina curves mbili f (x) =x na g (x) =1/x.Wao hupigwa tu katika quadrant ya kwanza. f (x) ni mstari wa diagonal unaoanzia asili na g (x) ni safu ya kupungua na y-axis kama asymptote ya wima na x-axis kama asymptote ya usawa. Grafu huingiliana kwenye (1,1). Kuna kanda ya kivuli kati ya grafu, imefungwa kwa haki na mstari saa x=4. Grafu ya pili ni curves mbili sawa. Kuna imara iliyoundwa na kupokezana eneo la kivuli kutoka kwenye grafu ya kwanza karibu na mhimili wa x-axis. — Kielelezo$\PageIndex{13}$: (a) Eneo kati ya grafu za kazi$f(x)=x$ na$g(x)=1/x$ zaidi ya muda$[1,4]$. (b) Kuzunguka eneo kuhusu$x$ **-axis** huzalisha imara ya mapinduzi na cavity katikati.

Tuna

\ [kuanza {align*} V &=^b_aπ\ kubwa [(f (x)) ^2- (g (x)) ^2\ kubwa]\, dx=π^4_1\ kushoto [x ^ 2\ kushoto (\ frac {1} {x}\ haki) ^2\ haki]\, dx\\
&=π\ kushoto. \ kushoto [\ frac {x^3} {3} +\ frac {1} {x}\ haki]\ haki|^4_1\\
&=\ dfrac {81π} {4}\,\ maandishi {vitengo} ^3. \ mwisho {align*}\]

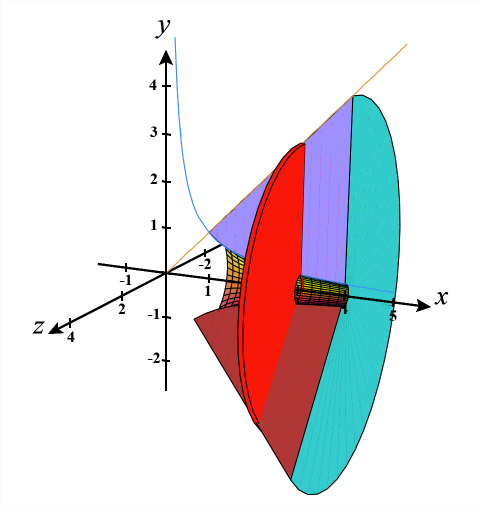
$clipboard_ec285765f5c0a0709a54ba430e31011a6.png$

Kielelezo$\PageIndex{13}$: (c) toleo nguvu ya hii imara ya mapinduzi yanayotokana kwa kutumia CalcPlot3D.

Zoezi$\PageIndex{5}$

Kupata kiasi cha imara ya mapinduzi sumu na yanazunguka eneo imepakana na grafu ya$f(x)=\sqrt{x}$ na$g(x)=1/x$ juu ya muda$[1,3]$ karibu $x$-axis.

Kidokezo: Grafu kazi ili kuamua ni grafu gani inayofunga juu na ambayo grafu huunda chini iliyofungwa, kisha utumie utaratibu kutoka kwa Mfano$\PageIndex{5}$.

Jibu: $\dfrac{10π}{3} \,\text{units}^3$

Kama ilivyo kwa njia ya disk, tunaweza pia kutumia njia ya washer kwa yabisi ya mapinduzi yanayotokana na yanazunguka eneo karibu na$y$ -axis. Katika kesi hii, sheria ifuatayo inatumika.

Utawala: Mbinu Washer kwa ajili ya Yabisi ya Mapinduzi kote$y$-axis

Tuseme$u(y)$ na$v(y)$ ni kazi zinazoendelea, zisizo za hasi kama hizo$y∈[c,d]$.$v(y)≤u(y)$ Hebu$Q$ kuashiria kanda imefungwa upande wa kulia na grafu ya$u(y)$, upande wa kushoto na grafu ya$v(y)$, chini na mstari$y=c$, na juu na mstari$y=d$. Kisha, kiasi cha imara ya mapinduzi yaliyoundwa na$Q$ kuzunguka$y$ -axis hutolewa na

\[V=∫^d_cπ\left[(u(y))^2−(v(y))^2\right]\,dy. \nonumber \]

Badala ya kuangalia mfano wa njia ya washer na$y$ -axis kama mhimili wa mapinduzi, sasa tunazingatia mfano ambao mhimili wa mapinduzi ni mstari mwingine zaidi ya moja ya shoka mbili za kuratibu. Njia hiyo ya jumla inatumika, lakini huenda ukahitaji kutazama jinsi ya kuelezea eneo la msalaba wa kiasi.

Mfano$\PageIndex{6}$:

Pata kiasi cha imara ya mapinduzi yaliyoundwa na yanazunguka eneo lililofungwa hapo juu$f(x)=4−x$ na chini na$x$ -axis juu ya muda$[0,4]$ karibu na mstari$y=−2.$

Suluhisho

Grafu ya kanda na imara ya mapinduzi huonyeshwa katika takwimu ifuatayo.

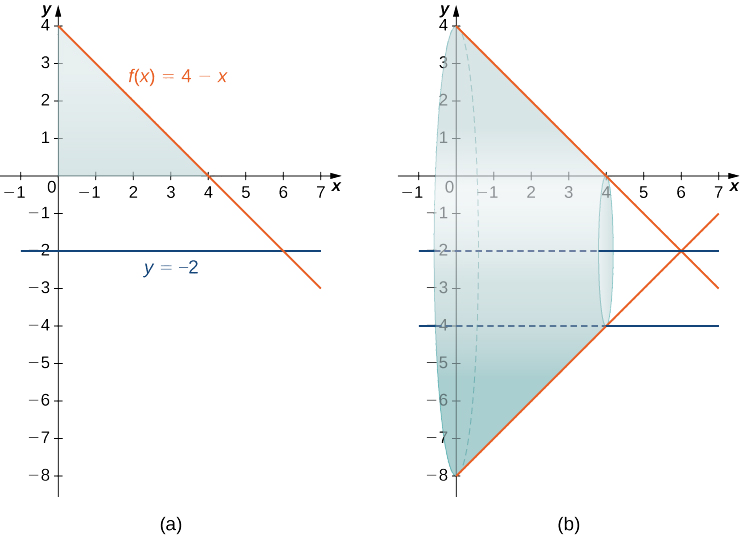
Takwimu hii ina grafu mbili. Grafu ya kwanza inaitwa “a” na ina curves mbili f (x) =4-x na -2. Kuna eneo la kivuli linalofanya pembetatu iliyofungwa na mstari wa kupungua f (x), mhimili wa y na x-axis. Grafu ya pili ni curves mbili sawa. Kuna imara iliyoundwa kwa kupokezana eneo la kivuli kutoka kwenye grafu ya kwanza karibu na mstari y =-2. Kuna silinda mashimo ndani ya imara iliyowakilishwa na mistari y=-2 na y=-4. — Kielelezo$\PageIndex{14}$: (a) Eneo kati ya grafu ya kazi$f(x)=4−x$ na **$x$-axis** juu ya muda$[0,4]$. (b) Kuzunguka kanda kuhusu mstari$y=−2$ huzalisha imara ya mapinduzi na shimo la cylindrical kupitia katikati yake.

Hatuwezi kutumia formula kiasi kwa tatizo hili moja kwa moja kwa sababu mhimili wa mapinduzi si moja ya shoka kuratibu. Hata hivyo, bado tunajua kwamba eneo la sehemu ya msalaba ni eneo la mduara wa nje chini ya eneo la mduara wa ndani. Kuangalia grafu ya kazi, tunaona radius ya mduara wa nje hutolewa na$f(x)+2,$ ambayo inafungua

$f(x)+2=(4−x)+2=6−x.$

Radi ya mduara wa ndani ni$g(x)=2.$ Kwa hiyo, tuna

\ [kuanza {align*} V &=^4_0π\ kushoto [(6—x) ^2—( 2) ^2\ kulia]\, dx\\
&=π^4_0 (x^2,112x+32)\, dx=π\ kushoto. \ kushoto [\ frac {x^3} {3} -6x^2+32x\ haki]\ haki|^4_0\\
&=\ dfrac {160π} {3}\,\ maandishi {vitengo} ^3. \ mwisho {align*}\]

Kielelezo$\PageIndex{14}$: (c) toleo nguvu ya hii imara ya mapinduzi yanayotokana kwa kutumia CalcPlot3D.

Zoezi$\PageIndex{6}$

Pata kiasi cha imara ya mapinduzi yaliyoundwa na yanazunguka eneo lililofungwa hapo juu$f(x)=x+2$ na grafu ya chini na$x$ -axis juu ya muda$[0,3]$ karibu na mstari$y=−1.$

Kidokezo: Tumia utaratibu kutoka kwa Mfano$\PageIndex{6}$.

Jibu: $60π$vitengo ³

Dhana muhimu

Integrals uhakika inaweza kutumika kupata kiasi cha yabisi. Kutumia njia ya slicing, tunaweza kupata kiasi kwa kuunganisha eneo la msalaba.
Kwa magumu ya mapinduzi, vipande vya kiasi mara nyingi ni disks na sehemu za msalaba ni miduara. Njia ya disks inahusisha kutumia njia ya slicing katika kesi fulani ambayo sehemu za msalaba ni miduara, na kutumia formula kwa eneo la mduara.
Ikiwa imara ya mapinduzi ina cavity katikati, vipande vya kiasi ni washers. Kwa njia ya washers, eneo la mduara wa ndani hutolewa kutoka eneo la mduara wa nje kabla ya kuunganisha.

Mlinganyo muhimu

Njia ya Disk kando ya$x$ mhimili

$\displaystyle V=∫^b_aπ\big[f(x)\big]^2\,dx$

Njia ya Disk kando ya$y$ mhimili

$\displaystyle V=∫^d_cπ\big[g(y)\big]^2\,dy$

Njia ya Washer

$\displaystyle V=∫^b_aπ\left[(f(x))^2−(g(x))^2\right]\,dx$

faharasa

sehemu nzima: makutano ya ndege na kitu imara

njia ya disk: kesi maalum ya njia ya slicing inayotumiwa na yabisi ya mapinduzi wakati vipande ni disks

njia ya kukata: njia ya kuhesabu kiasi cha imara ambayo inahusisha kukata imara vipande vipande, kukadiria kiasi cha kila kipande, kisha kuongeza makadirio haya ili kufikia makadirio ya kiasi cha jumla; kama idadi ya vipande huenda kwa infinity, makadirio haya inakuwa muhimu ambayo inatoa thamani halisi ya kiasi

imara ya mapinduzi: imara yanayotokana na yanazunguka kanda katika ndege karibu na mstari katika ndege hiyo

njia ya washer: kesi maalum ya njia ya slicing inayotumiwa na yabisi ya mapinduzi wakati vipande ni washers

Mkakati wa Kutatua Matatizo: Kutafuta Kiasi kwa Njia ya Slicing

Mfano\(\PageIndex{1}\): Deriving the Formula for the Volume of a Pyramid

Zoezi\(\PageIndex{1}\)

Mfano\(\PageIndex{2}\): Using the Slicing Method to find the Volume of a Solid of Revolution

Zoezi\(\PageIndex{2}\)

Njia ya Disk

Mfano\(\PageIndex{3}\): Using the Disk Method to Find the Volume of a Solid of Revolution 1

Zoezi\(\PageIndex{3}\)

Utawala: Method Disk kwa Solids ya Mapinduzi kote\(y\)-axis

Mfano\(\PageIndex{4}\): Using the Disk Method to Find the Volume of a Solid of Revolution 2

Zoezi\(\PageIndex{4}\)

Kanuni: Njia ya Washer

Mfano\(\PageIndex{5}\): Using the Washer Method

Zoezi\(\PageIndex{5}\)

Utawala: Mbinu Washer kwa ajili ya Yabisi ya Mapinduzi kote\(y\)-axis

Mfano\(\PageIndex{6}\):

Zoezi\(\PageIndex{6}\)