5.2: Integral ya uhakika

Malengo ya kujifunza

• Hali ya ufafanuzi wa muhimu ya uhakika.
• Eleza masharti integrand, mipaka ya ushirikiano, na kutofautiana ya ushirikiano.
• Eleza wakati kazi ni integrable.
• Eleza uhusiano kati ya eneo la uhakika na la wavu.
• Tumia jiometri na mali ya integrals uhakika ili kutathmini yao.
• Tumia thamani ya wastani ya kazi.

Katika sehemu iliyotangulia sisi defined eneo chini ya Curve katika suala la Riemann kiasi:

\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]

Hata hivyo, ufafanuzi huu ulikuja na vikwazo. Sisi required kuwa\(f(x)\) kuendelea na nonnegative. Kwa bahati mbaya, matatizo halisi ya ulimwengu hayatimii vikwazo hivi daima. Katika sehemu hii, tunaangalia jinsi ya kutumia dhana ya eneo chini ya pembe kwa seti pana ya kazi kupitia matumizi ya muhimu ya uhakika.

Ufafanuzi na Uthibitisho

Muhimu wa uhakika huzalisha dhana ya eneo chini ya pembe. Tunainua mahitaji ambayo\(f(x)\) yanaendelea na yasiyo ya hasi, na kufafanua muhimu ya uhakika kama ifuatavyo.

Ufafanuzi: Hakika Integral

Kama\(f(x)\) ni kazi defined juu\([a,b],\) ya muda muhimu uhakika wa\(f\) kutoka\(a\) kwa\(b\) ni kutolewa na

\[∫^b_af(x)\,dx=\lim_{n→∞} \sum_{i=1}^nf(x^∗_i)Δx, \nonumber \]

zinazotolewa kikomo ipo. Kama kikomo hii ipo, kazi\(f(x)\) inasemekana kuwa integrable juu ya\([a,b]\), au ni kazi integrable.

Ishara muhimu katika ufafanuzi uliopita inapaswa kuangalia ukoo. Tumeona nukuu sawa katika sura juu ya Matumizi ya derivatives, ambapo tulitumia muda usiojulikana ishara muhimu (bila\(a\) na\(b\) juu na chini) kuwakilisha antiderivative. Ingawa notation kwa integrals muda usiojulikana inaweza kuangalia sawa na nukuu kwa muhimu uhakika, wao si sawa. Muhimu wa uhakika ni namba. Muhimu usio na kipimo ni familia ya kazi. Baadaye katika sura hii tunachunguza jinsi dhana hizi zinahusiana. Hata hivyo, makini ya karibu lazima daima kulipwa kwa nukuu ili tunajua kama sisi ni kufanya kazi na muhimu uhakika au muhimu kwa muda usiojulikana.

Integral nukuu inakwenda nyuma mwishoni mwa karne ya kumi na saba na ni moja ya michango ya Gottfried Wilhelm Leibniz, ambaye mara nyingi huchukuliwa kuwa codiscoverer ya calculus, pamoja na Isaac Newton. Ishara ya ushirikiano\(∫\) ni mviringo\(S\), inayoonyesha sigma au summation. Katika muhimu ya uhakika, juu na chini ya ishara ya summation ni mipaka ya muda,\([a,b].\) Nambari\(a\) na\(b\) ni\(x\) -maadili na huitwa mipaka ya ushirikiano; hasa,\(a\) ni kikomo cha chini na\(b\) ni kikomo cha juu. Ili kufafanua, tunatumia kikomo cha neno kwa njia mbili tofauti katika muktadha wa muhimu. Kwanza, tunazungumzia juu ya kikomo cha jumla kama\(n→∞.\) Pili, mipaka ya kanda inaitwa mipaka ya ushirikiano.

Tunaita kazi\(f(x)\) integrand, na\(dx\) inaonyesha kwamba\(f(x)\) ni kazi kwa heshima na\(x\), kuitwa variable ya ushirikiano. Kumbuka kwamba, kama index kwa jumla, kutofautiana kwa ushirikiano ni variable dummy, na haina athari juu ya hesabu ya muhimu. Tunaweza kutumia variable yoyote tunapenda kama variable ya ushirikiano:

\[∫^b_af(x)\,dx=∫^b_af(t)\,dt=∫^b_af(u)\,du \nonumber \]

Hapo awali, tulijadili ukweli kwamba ikiwa\(f(x)\) unaendelea\([a,b],\) basi kikomo\(\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\) kipo na ni cha pekee. Hii inasababisha theorem ifuatayo, ambayo tunasema bila ushahidi.

Kazi zinazoendelea Ni integrable

Kama\(f(x)\) ni kuendelea\([a,b]\), basi\(f\) ni integrable juu\([a,b].\)

Kazi ambazo si kuendelea juu bado\([a,b]\) inaweza kuwa integrable, kulingana na hali ya discontinuities. Kwa mfano, kazi na idadi ya mwisho ya discontinuities ya kuruka au discontinuities inayoondolewa kwenye muda uliofungwa ni integrable.

Pia ni muhimu kuzingatia hapa kwamba tumehifadhi matumizi ya ugawaji wa kawaida katika kiasi cha Riemann. Kizuizi hiki sio lazima sana. Sehemu yoyote inaweza kutumika kutengeneza jumla ya Riemann. Hata hivyo, ikiwa sehemu isiyo ya kawaida hutumiwa kufafanua muhimu ya uhakika, haitoshi kuchukua kikomo kama idadi ya subinternations inakwenda infinity. Badala yake, ni lazima kuchukua kikomo kama upana wa subinterval kubwa huenda sifuri. Hii utangulizi nukuu kidogo ngumu zaidi katika mipaka yetu na inafanya mahesabu ngumu zaidi bila kweli kupata ufahamu mkubwa zaidi, hivyo sisi fimbo na partitions mara kwa mara kwa kiasi Riemann.

Mfano\(\PageIndex{1}\): Evaluating an Integral Using the Definition

Matumizi ufafanuzi wa muhimu uhakika kutathmini\(\displaystyle ∫^2_0x^2\,dx.\) Matumizi haki-mwisho makadirio ya kuzalisha Riemann jumla.

Suluhisho

Sisi kwanza wanataka kuanzisha jumla Riemann. Kulingana na mipaka ya ushirikiano, tuna\(a=0\) na\(b=2\). Kwa\(i=0,1,2,…,n\), hebu\(P={x_i}\) kuwa kizigeu mara kwa mara ya\([0,2].\) Kisha

\[Δx=\dfrac{b−a}{n}=\dfrac{2}{n}. \nonumber \]

Kwa kuwa tunatumia makadirio ya mwisho ya haki ili kuzalisha kiasi cha Riemann\(i\), kwa kila mmoja, tunahitaji kuhesabu thamani ya kazi kwenye mwisho wa haki\([x_{i−1},x_i].\) wa muda Mwisho wa mwisho wa muda ni\(x_i\), na kwa kuwa\(P\) ni sehemu ya kawaida,

\[x_i=x_0+iΔx=0+i\left[\dfrac{2}{n}\right]=\dfrac{2i}{n}.\nonumber \]

Hivyo, thamani ya kazi katika mwisho wa mwisho wa muda ni

\[f(x_i)=x^2_i=\left(\dfrac{2i}{n}\right)^2=\dfrac{4i^2}{n^2}.\nonumber \]

Kisha jumla ya Riemann inachukua fomu

\[\sum_{i=1}^nf(x_i)Δx=\sum_{i=1}^n\left(\dfrac{4i^2}{n^2}\right)\dfrac{2}{n}=\sum_{i=1}^n\dfrac{8i^2}{n^3}=\dfrac{8}{n^3}\sum_{i=1}^ni^2.\nonumber \]

Kutumia formula ya summation kwa\(\displaystyle \sum_{i=1}^ni^2\), tuna

\[\begin{align*} \sum_{i=1}^nf(x_i)Δx &=\dfrac{8}{n^3}\sum_{i=1}^ni^2 \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{n(n+1)(2n+1)}{6}\right] \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{2n^3+3n^2+n}{6}\right] \\[4pt] &=\dfrac{16n^3+24n^2+n}{6n^3} \\[4pt] &=\dfrac{8}{3}+\dfrac{4}{n}+\dfrac{1}{6n^2}. \end{align*}\]

Sasa, ili kuhesabu muhimu ya uhakika, tunahitaji kuchukua kikomo kama\(n→∞\). Tunapata

\ [kuanza {align*} ^2_0x^2dx &=\ lim_ {n → Δ}\ sum_ {i = 1} ^nf (x_i) Δx\\ [4pt]
&=\ lim_ {n→ Δ}\ kushoto (\ dfrac {8} {3} +\ dfrac {4} {n} +\ dfrac {1} {6n^2}\ haki)\\ [4pt]
&=\ lim_ {n → Δ}\ kushoto (\ dfrac {8} {3}\ haki) +\ lim_ {n → Δ}\ kushoto (\ dfrac {4} {n}\ haki) +\ lim_ {n → Δ}\ kushoto (\ dfrac {1}} {6n ^ 2}\ haki)\\ [4pt]
&=\ dfrac {8} {3} +0+0 =\ dfrac {8} {3}. \ mwisho {align*}\]

Zoezi\(\PageIndex{1}\)

Tumia ufafanuzi wa muhimu ya kutathmini\(\displaystyle ∫^3_0(2x−1)\,dx\).

Matumizi haki-mwisho makadirio ya kuzalisha Riemann jumla.

Kidokezo

Tumia mkakati wa kutatua kutoka Mfano\(\PageIndex{1}\).

Jibu

6

Kutathmini Integrals uhakika

Kuchunguza integrals uhakika kwa njia hii inaweza kuwa mbaya sana kwa sababu ya utata wa mahesabu. Baadaye katika sura hii sisi kuendeleza mbinu kwa ajili ya kutathmini integrals uhakika bila kuchukua mipaka ya Riemann kiasi. Hata hivyo, kwa sasa, tunaweza kutegemea ukweli kwamba integrals uhakika kuwakilisha eneo chini ya Curve, na tunaweza kutathmini integrals uhakika kwa kutumia formula geometric kuhesabu eneo hilo. Sisi kufanya hivyo kuthibitisha kwamba integrals uhakika kufanya, kwa kweli, kuwakilisha maeneo, hivyo tunaweza kisha kujadili nini cha kufanya katika kesi ya Curve ya kazi kuacha chini\(x\) -axis.

Mfano\(\PageIndex{2}\): Using Geometric Formulas to Calculate Definite Integrals

Tumia formula kwa eneo la mduara ili kutathmini\(\displaystyle ∫^6_3\sqrt{9−(x−3)^2}\,dx\).

Suluhisho

Kazi inaelezea semicircle na radius 3. Ili kupata

\[∫^6_3\sqrt{9−(x−3)^2}\,dx \nonumber \]

tunataka kupata eneo chini ya Curve juu ya muda Fomu\([3,6].\) ya eneo la mduara ni\(A=πr^2\). Eneo la semicircle ni nusu tu eneo la mduara, au\(A=\dfrac{1}{2}πr^2\). Eneo la kivuli katika Kielelezo\(\PageIndex{1}\) kinashughulikia nusu moja ya semicircle, au\(A=\dfrac{1}{4}πr^2\). Hivyo,

\[∫^6_3\sqrt{9−(x−3)^2}\,dx=\dfrac{1}{4}π(3)^2=\dfrac{9}{4}π≈7.069. \nonumber \]

Kielelezo\(\PageIndex{1}\): Thamani ya muhimu ya kazi\(f(x)\) juu ya muda\([3,6]\) ni eneo la kanda la kivuli.

Zoezi\(\PageIndex{2}\)

Tumia formula kwa eneo la trapezoid kutathmini\(\displaystyle ∫^4_2(2x+3)\,dx\).

Kidokezo

Graph kazi\(f(x)\) na uhesabu eneo chini ya kazi kwa muda\([2,4].\)

Jibu

Vitengo vya mraba 18

Eneo na Integral ya uhakika

Wakati sisi defined muhimu uhakika, sisi lile mahitaji kwamba\(f(x)\) kuwa nonnegative. Lakini tunawezaje kutafsiri “eneo chini ya pembe” wakati\(f(x)\) ni hasi?

Eneo lililosainiwa

Hebu kurudi Riemann jumla. Fikiria, kwa mfano, kazi\(f(x)=2−2x^2\) (iliyoonyeshwa kwenye Kielelezo\(\PageIndex{2}\)) kwa muda\([0,2]\). Tumia\(n=8\) na uchague {\(x^∗_i\)} kama mwisho wa kushoto wa kila kipindi. Kujenga mstatili kwenye kila subinterval ya urefu\(f(x^∗_i)\) na upana\(Δx\). Wakati\(f(x^∗_i)\) ni chanya, bidhaa\(f(x^∗_i)Δx\) inawakilisha eneo la mstatili, kama hapo awali. Wakati\(f(x^∗_i)\) ni hasi, hata hivyo, bidhaa\(f(x^∗_i)Δx\) inawakilisha hasi ya eneo la mstatili. Jumla ya Riemann kisha inakuwa

\[\sum_{i=1}^8f(x^∗_i)Δx= (\text{Area of rectangles above the }x\text{-axis})−(\text{Area of rectangles below the }x\text{-axis}) \nonumber \]

Kielelezo\(\PageIndex{2}\): Kwa kazi ambayo ni sehemu mbaya, jumla ya Riemann ni eneo la mstatili juu ya\(x\) -axis chini ya eneo la rectangles chini ya\(x\) -axis.

Kuchukua kikomo kama\(n→∞,\) jumla Riemann inakaribia eneo kati ya Curve juu\(x\) -axis na\(x\) -axis, chini ya eneo kati ya Curve chini\(x\) -axis na\(x\) -axis, kama inavyoonekana katika Kielelezo\(\PageIndex{3}\). Kisha,

\[\int^2_0f(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(c_i)Δx=A_1−A_2. \nonumber \]

Kiasi\(A_1−A_2\) kinachoitwa eneo lililosainiwa wavu.

Kielelezo\(\PageIndex{3}\): Katika kikomo, muhimu ya uhakika ni sawa na eneo\(A_1\) chini ya eneo\(A_2\), au eneo lililosainiwa wavu.

Angalia kwamba eneo lililosainiwa wavu linaweza kuwa chanya, hasi, au sifuri. Ikiwa eneo la juu\(x\) -axis ni kubwa, eneo lililosainiwa wavu ni chanya. Ikiwa eneo chini ya\(x\) -axis ni kubwa, eneo la saini la wavu ni hasi. Ikiwa maeneo ya juu na chini ya\(x\) -axis ni sawa, eneo lililosainiwa wavu ni sifuri.

Mfano\(\PageIndex{3}\): Finding the Net Signed Area

Pata eneo lililosainiwa wavu kati ya pembe ya kazi\(f(x)=2x\) na\(x\) -axis juu ya muda\([−3,3].\)

Suluhisho

Kazi hutoa mstari wa moja kwa moja unaounda pembetatu mbili: moja kutoka\(x=−3\) kwa\(x=0\) na nyingine kutoka\(x=0\) kwa\(x=3\) (Kielelezo\(\PageIndex{4}\)). Kutumia formula ya kijiometri kwa eneo la pembetatu\(A=\dfrac{1}{2}bh\), eneo la pembetatu\(A_1\), juu ya mhimili, ni

\(A_1=\dfrac{1}{2}3(6)=9\),

ambapo\(3\) ni msingi na\(2(3)=6\) ni urefu. Eneo la pembetatu\(A_2\), chini ya mhimili, ni

\(A_2=\dfrac{1}{2}(3)(6)=9,\)

ambapo\(3\) ni msingi na\(6\) ni urefu. Hivyo, eneo wavu ni

\(\displaystyle ∫^3_{−3}2x\,dx=A_1−A_2=9−9=0.\)

Kielelezo\(\PageIndex{4}\): Eneo la juu ya pembe na chini ya\(x\) -axis ni sawa na eneo chini ya pembe na juu ya\(x\) -axis.

Uchambuzi

Ikiwa\(A_1\) ni eneo la juu\(x\) -axis na\(A_2\) ni eneo chini ya\(x\) -axis, basi eneo la wavu ni\(A_1−A_2\). Kwa kuwa maeneo ya pembetatu mbili ni sawa, eneo la wavu ni sifuri.

Zoezi\(\PageIndex{3}\)

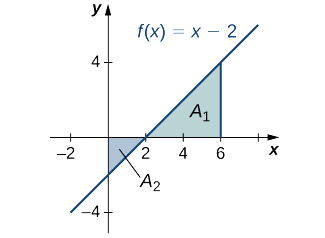
Kupata wavu saini eneo la\(f(x)=x−2\) zaidi ya muda\([0,6]\), mfano katika picha zifuatazo.

Kidokezo

Tumia njia ya kutatua ilivyoelezwa katika Mfano\(\PageIndex{3}\).

Jibu

6

Jumla ya Eneo

Matumizi moja ya muhimu ya uhakika ni kutafuta uhamisho wakati unapewa kazi ya kasi. Ikiwa\(v(t)\) inawakilisha kasi ya kitu kama kazi ya wakati, basi eneo chini ya curve inatuambia jinsi mbali kitu ni kutoka nafasi yake ya awali. Hii ni matumizi muhimu sana ya muhimu, na tunaiangalia kwa undani zaidi baadaye katika sura. Kwa sasa, sisi ni kwenda tu kuangalia baadhi ya misingi ya kupata hisia kwa jinsi hii kazi kwa kusoma kasi ya mara kwa mara.

Wakati kasi ni mara kwa mara, eneo chini ya Curve ni tu kasi mara wakati. Wazo hili tayari limejulikana sana. Ikiwa gari linasafiri mbali na nafasi yake ya kuanzia kwenye mstari wa moja kwa moja kwa kasi ya\(70\) mph kwa\(2\) masaa, basi ni\(140\) maili mbali na nafasi yake ya awali (Kielelezo\(\PageIndex{5}\)). Kutumia nukuu muhimu, tuna

\[∫^2_0 70\,dt=140 \,\text{miles}. \nonumber \]

Kielelezo\(\PageIndex{5}\): Eneo chini ya pembe\(v(t)=70\) inatuambia jinsi gari liko mbali na mwanzo wake kwa wakati fulani.

Katika mazingira ya makazi yao, eneo lililosainiwa wavu linatuwezesha kuzingatia mwelekeo. Ikiwa gari linasafiri kaskazini moja kwa moja kwa kasi ya 60 mph kwa masaa 2, ni maili 120 kaskazini ya nafasi yake ya kuanzia. Ikiwa gari linageuka na kusafiri kusini kwa kasi ya 40 mph kwa masaa 3, itarudi kwenye nafasi ya kuanzia (Kielelezo\(\PageIndex{6}\)). Tena, kwa kutumia nukuu muhimu, tuna

\[\int^2_060\,dt+∫^5_2−40\,dt=120−120=0.\nonumber \]

Katika kesi hii makazi yao ni sifuri.

Kielelezo\(\PageIndex{6}\): Eneo la juu ya mhimili na eneo chini ya mhimili ni sawa, hivyo eneo lililosainiwa wavu ni sifuri.

Tuseme tunataka kujua ni umbali gani gari husafiri kwa ujumla, bila kujali mwelekeo. Katika kesi hii, tunataka kujua eneo kati ya Curve na\(t\) -axis, bila kujali kama eneo hilo ni juu au chini ya mhimili. Hii inaitwa eneo la jumla.

Graphically, ni rahisi kufikiria kuhesabu eneo la jumla kwa kuongeza maeneo ya juu ya mhimili na maeneo chini ya mhimili (badala ya kuondoa maeneo chini ya mhimili, kama tulivyofanya na eneo lililosainiwa wavu). Ili kukamilisha hili hesabu, sisi kutumia thamani kamili kazi. Hivyo, umbali wa jumla alisafiri kwa gari ni

\[\int^2_0|60|\,dt+∫^5_2|−40|\,dt=∫^2_060\,dt+∫^5_240\,dt=120+120=240.\nonumber \]

Kuleta mawazo haya pamoja rasmi, tunasema ufafanuzi wafuatayo.

Ufafanuzi: Eneo la Saini

Hebu\(f(x)\) kuwa kazi integrable defined juu ya muda\([a,b]\). Hebu\(A_1\) kuwakilisha eneo kati\(f(x)\) na\(x\) -axis kwamba liko juu ya mhimili na basi\(A_2\) kuwakilisha eneo kati\(f(x)\) na\(x\) -axis kwamba iko chini ya mhimili. Kisha, eneo lililosainiwa wavu kati\(f(x)\) na\(x\) -axis linatolewa na

\[∫^b_af(x)\,dx=A_1−A_2. \nonumber \]

Eneo la jumla kati\(f(x)\) na\(x\) -axis linatolewa na

\[∫^b_a|f(x)|\,dx=A_1+A_2. \nonumber \]

Mfano\(\PageIndex{4}\): Finding the Total Area

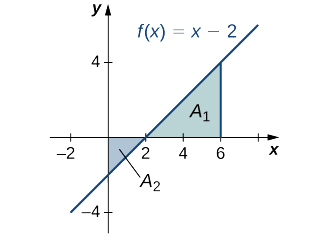
Pata eneo la jumla kati\(f(x)=x−2\) na\(x\) -axis juu ya muda\([0,6].\)

Suluhisho

Tumia\(x\) -intercept kama\((2,0)\) (kuweka\(y=0,\) kutatua kwa\(x\)). Ili kupata eneo la jumla, chukua eneo chini ya\(x\) -axis juu ya subinterval\([0,2]\) na uongeze kwenye eneo la juu\(x\) -axis kwenye subinterval\([2,6]\) (Kielelezo\(\PageIndex{7}\)).

Kielelezo\(\PageIndex{7}\): Eneo la jumla kati ya mstari na\(x\) -axis juu\([0,6]\) ni\(A_2\) pamoja\(A_1\).

Tuna

\[∫^6_0|(x−2)|\,dx=A_2+A_1. \nonumber \]

Kisha, kwa kutumia formula kwa eneo la pembetatu, tunapata

\[A_2=\dfrac{1}{2}bh=\dfrac{1}{2}⋅2⋅2=2 \nonumber \]

\[A_1=\dfrac{1}{2}bh=\dfrac{1}{2}⋅4⋅4=8. \nonumber \]

Eneo la jumla, basi, ni

\[A_1+A_2=8+2=10\,\text{units}^2. \nonumber \]

Zoezi\(\PageIndex{4}\)

Pata eneo la jumla kati ya kazi\(f(x)=2x\) na\(x\) -axis juu ya muda\([−3,3].\)

Kidokezo

Tathmini ya mkakati wa kutatua katika Mfano\(\PageIndex{4}\).

Jibu

\(18\,\text{units}^2\)

Mali ya Integral ya uhakika

Mali ya integrals isiyojulikana hutumika kwa integrals uhakika pia. Integrals uhakika pia kuwa na mali zinazohusiana na mipaka ya ushirikiano. Hizi mali, pamoja na sheria za ushirikiano kwamba sisi kuchunguza baadaye katika sura hii, kutusaidia kuendesha maneno kutathmini integrals uhakika.

Kanuni: Mali ya Integral ya uhakika

1. \[ \begin{equation} ∫^a_af(x)\,dx=0 \end{equation} \nonumber \]

Ikiwa mipaka ya ushirikiano ni sawa, muhimu ni mstari tu na haina eneo.

2. \[∫^a_bf(x)\,dx=−∫^b_af(x)\,dx \nonumber \]

Ikiwa mipaka inabadilishwa, kisha uweke ishara hasi mbele ya muhimu.

3. \[∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx \nonumber \]

Muhimu wa jumla ni jumla ya integrals.

4. \[∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx \nonumber \]

Muhimu wa tofauti ni tofauti ya integrals.

5. \[∫^b_acf(x)\,dx=c∫^b_af(x)\,dx \nonumber \]

kwa mara kwa mara\(c\). Muhimu wa bidhaa ya mara kwa mara na kazi ni sawa na mara kwa mara kuongezeka kwa muhimu ya kazi.

6. \[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx \nonumber \]

Ingawa formula hii kwa kawaida inatumika wakati\(c\) ni kati\(a\) na\(b\), formula ana kwa maadili yote ya\(a\),\(b\), na\(c\), zinazotolewa\(f(x)\) ni integrable juu ya muda kubwa.

Mfano\(\PageIndex{5}\): Using the Properties of the Definite Integral

Tumia mali ya muhimu ya uhakika ili kuelezea umuhimu wa uhakika wa\(f(x)=−3x^3+2x+2\) zaidi ya muda\([−2,1]\) kama jumla ya vipengele vitatu vya uhakika.

Suluhisho

Kutumia nukuu muhimu,\(\displaystyle ∫^1_{−2}(−3x^3+2x+2)\,dx.\) tuna Sisi kuomba mali 3. na 5. kupata

\ [kuanza {align*} ^1_ {¯ 2} (-3x^3+2x+2)\, dx =^1_ {¯ 2} -3x^3\, dx+^1_ {¯ 2} 2x\, dx+^1_ {¯ 2} 2\, dx\\ [4pt]
=-3^1_ {¯ 2} x ^ 3\, dx+2^1_ {¯ 2} x\, dx+^1_ {¯ 2} 2\, dx. \ mwisho {align*}\ nonumber\]

Zoezi\(\PageIndex{5}\)

Tumia mali ya muhimu ya uhakika ili kuelezea umuhimu wa uhakika wa\(f(x)=6x^3−4x^2+2x−3\) zaidi ya muda\([1,3]\) kama jumla ya viungo vinne vya uhakika.

Kidokezo

Tumia mkakati wa kutatua kutoka Mfano\(\PageIndex{5}\) na mali ya integrals uhakika.

Jibu

\(\displaystyle 6∫^3_1x^3\,dx−4∫^3_1x^2\,dx+2∫^3_1x\,dx−∫^3_13\,dx \)

Mfano\(\PageIndex{6}\): Using the Properties of the Definite Integral

Kama inajulikana kuwa\(\displaystyle ∫^8_0f(x)\,dx=10\) na\(\displaystyle ∫^5_0f(x)\,dx=5\), kupata thamani ya\(\displaystyle ∫^8_5f(x)\,dx\).

Suluhisho

Na mali 6,

\[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx. \nonumber \]

Hivyo,

\[ \begin{align*} ∫^8_0f(x)\,dx&=∫^5_0f(x)\,dx+∫^8_5f(x)\,dx \\[4pt] 10 &=5+∫^8_5f(x)\,dx \\[4pt] 5 &=∫^8_5f(x)\,dx. \end{align*}\]

Zoezi\(\PageIndex{6}\)

Kama inajulikana kuwa\(\displaystyle ∫^5_1f(x)\,dx=−3\) na\(\displaystyle ∫^5_2f(x)\,dx=4\), kupata thamani ya\(\displaystyle ∫^2_1f(x)\,dx.\)

Kidokezo

Tumia mkakati wa kutatua kutoka Mfano\(\PageIndex{6}\) na utawala juu ya mali ya integrals uhakika.

Jibu

\(−7\)

Kulinganisha Mali ya Integrals

picha wakati mwingine kutuambia zaidi kuhusu kazi ya matokeo ya hesabu. Kulinganisha kazi na grafu zao kama vile kwa maneno yao ya algebraic mara nyingi huweza kutoa ufahamu mpya katika mchakato wa ushirikiano. Intuitively, tunaweza kusema kwamba kama kazi\(f(x)\) ni juu ya kazi nyingine\(g(x)\), basi eneo kati\(f(x)\) na\(x\) -axis ni kubwa kuliko eneo kati\(g(x)\) na\(x\) -axis. Hii ni kweli kulingana na muda ambao kulinganisha hufanywa. Mali ya integrals uhakika ni halali kama\(a<b,\,a=b\), au\(a>b\). Mali zifuatazo, hata hivyo, zinahusu tu kesi\(a≤b\), na hutumiwa wakati tunataka kulinganisha ukubwa wa integrals.

Theorem ya kulinganisha

i Kama\(f(x)≥0\) kwa\(a≤x≤b\), basi

\[∫^b_af(x)\,dx≥0. \nonumber \]

ii. Ikiwa\(f(x)≥g(x)\) kwa\(a≤x≤b\), basi

\[∫^b_af(x)\,dx≥∫^b_ag(x)\,dx. \nonumber \]

iii. Kama\(m\) na\(M\) ni constants vile kwamba\(m≤f(x)≤M\) kwa\(a≤x≤b\), basi

\[m(b−a)≤∫^b_af(x)\,dx≤M(b−a). \nonumber \]

Mfano\(\PageIndex{7}\): Comparing Two Functions over a Given Interval

Linganisha\(f(x)=\sqrt{1+x^2}\) na\(g(x)=\sqrt{1+x}\) juu ya muda\([0,1]\).

Suluhisho

Graphing kazi hizi ni muhimu kuelewa jinsi kulinganisha juu ya muda\([0,1].\) Awali, wakati graphed juu ya calculator graphing,\(f(x)\) inaonekana kuwa juu ya\(g(x)\) kila mahali. Hata hivyo, kwa muda\([0,1]\), grafu zinaonekana kuwa juu ya kila mmoja. Tunahitaji kuvuta ili kuona kwamba, kwa muda\([0,1],\,g(x)\) ni hapo juu\(f(x)\). Kazi mbili zinaingiliana\(x=0\) na\(x=1\) (Kielelezo\(\PageIndex{8}\)).

Kielelezo\(\PageIndex{8}\): (a) Kazi\(f(x)\) inaonekana juu ya kazi\(g(x)\) isipokuwa zaidi ya muda\([0,1]\) (b) Kuangalia grafu sawa na zoom kubwa inaonyesha hii wazi zaidi.

Tunaweza kuona kutoka grafu kwamba zaidi ya muda\([0,1],\,g(x)≥f(x)\). Kulinganisha integrals juu ya muda maalum\([0,1],\) sisi pia kuona kwamba\(\displaystyle ∫^1_0g(x)\,dx≥∫^1_0f(x)\,dx\) (Kielelezo\(\PageIndex{9}\)). Eneo nyembamba, nyekundu-kivuli linaonyesha ni tofauti gani kati ya vipengele hivi viwili kwa muda\([0,1].\)

Kielelezo\(\PageIndex{9}\): (a) Grafu inaonyesha kwamba zaidi ya muda\([0,1],g(x)≥f(x),\) ambapo usawa unashikilia tu mwisho wa muda. (b) Kuangalia grafu sawa na zoom kubwa inaonyesha hii wazi zaidi.

Wastani wa Thamani ya Kazi

Mara nyingi tunahitaji kupata wastani wa seti ya namba, kama vile daraja la wastani la mtihani. Tuseme umepokea alama za mtihani zifuatazo katika darasa lako la algebra: 89, 90, 56, 78, 100, na 69. Muhula wako daraja ni wastani wako wa alama mtihani na unataka kujua nini daraja kutarajia. Tunaweza kupata wastani kwa kuongeza alama zote na kugawa kwa idadi ya alama. Katika kesi hii, kuna alama sita za mtihani. Hivyo,

\[\dfrac{89+90+56+78+100+69}{6}=\dfrac{482}{6}≈80.33. \nonumber \]

Kwa hiyo, wastani wa daraja lako la mtihani ni takriban 80.33, ambalo linatafsiriwa kwa B katika shule nyingi.

Tuseme, hata hivyo,\(v(t)\) kwamba tuna kazi ambayo inatupa kasi ya kitu wakati wowote\(t\), na tunataka kupata kitu ya wastani wa kasi. Kazi\(v(t)\) inachukua idadi usio wa maadili, hivyo hatuwezi kutumia mchakato tu ilivyoelezwa. Kwa bahati nzuri, tunaweza kutumia muhimu ya uhakika ili kupata thamani ya wastani ya kazi kama hii.

Hebu\(f(x)\) uendelee juu ya muda\([a,b]\) na uache\([a,b]\) kugawanywa katika sehemu ndogo za upana\(Δx=(b−a)/n\). Chagua mwakilishi\(x^∗_i\) katika kila subinterval na uhesabu\(f(x^∗_i)\) kwa\(i=1,2,…,n.\) Kwa maneno mengine, fikiria kila mmoja\(f(x^∗_i)\) kama sampuli ya kazi juu ya kila subinterval. Thamani ya wastani ya kazi inaweza kuwa takriban kama

\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}, \nonumber \]

ambayo kimsingi ni kujieleza sawa kutumika kwa mahesabu ya wastani wa maadili ya kipekee.

Lakini tunajua\(Δx=\dfrac{b−a}{n},\) hivyo\(n=\dfrac{b−a}{Δx}\), na sisi kupata

\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}=\dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{\left(\dfrac{b−a}{Δx}\right)}. \nonumber \]

Kufuatia kupitia na algebra, nambari ni jumla ambayo inawakilishwa kama\(\sum_{i=1}^nf(x∗i),\) na sisi ni kugawa na sehemu. Ili kugawanywa na sehemu, ingiza denominator na uongeze. Hivyo, thamani ya takriban kwa thamani ya wastani ya kazi hutolewa na

\[\dfrac{\sum_{i=1}^nf(x^∗_i)}{\left(\dfrac{b−a}{Δx}\right)}=\left(\dfrac{Δx}{b−a}\right)\sum_{i=1}^nf(x^∗_i)=\left(\dfrac{1}{b−a}\right)\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]

Hii ni jumla Riemann. Kisha, ili kupata thamani halisi ya wastani, kuchukua kikomo kama\(n\) inakwenda infinity. Hivyo, thamani ya wastani ya kazi hutolewa na

\[\dfrac{1}{b−a}\lim_{n→∞}\sum_{i=1}^nf(x_i)Δx=\dfrac{1}{b−a}∫^b_af(x)dx. \nonumber \]

Ufafanuzi: Wastani wa Thamani ya Kazi

Hebu\(f(x)\) uendelee zaidi ya muda\([a,b]\). Kisha, thamani ya wastani ya kazi\(f(x)\) (au\(f_{ave}\)) juu\([a,b]\) inatolewa na

\[f_{ave}=\dfrac{1}{b−a}∫^b_af(x)\,dx. \label{averagevalue} \]

Mfano\(\PageIndex{8}\): Finding the Average Value of a Linear Function

Pata thamani ya wastani ya\(f(x)=x+1\) zaidi ya muda\([0,5].\)

Suluhisho

Kwanza, graph kazi kwenye kipindi kilichoelezwa, kama inavyoonekana kwenye Kielelezo\(\PageIndex{10}\).

Takwimu:\(\PageIndex{10}\) Grafu inaonyesha eneo chini ya kazi\((x)=x+1\)\([0,5].\)

Kanda ni trapezoid amelala upande wake, hivyo tunaweza kutumia formula eneo kwa trapezoid\(A=\dfrac{1}{2}h(a+b),\) ambapo\(h\) inawakilisha urefu,\(a\) na\(b\) kuwakilisha pande mbili sambamba. Kisha,

\(\displaystyle ∫^5_0x+1\,dx=\dfrac{1}{2}h(a+b)=\dfrac{1}{2}⋅5⋅(1+6)=\dfrac{35}{2}\).

Hivyo thamani ya wastani ya kazi ni

\(\displaystyle \dfrac{1}{5−0}∫^5_0x+1\,dx=\dfrac{1}{5}⋅\dfrac{35}{2}=\dfrac{7}{2}\).

Zoezi\(\PageIndex{7}\)

Pata thamani ya wastani ya\(f(x)=6−2x\) zaidi ya muda\([0,3].\)

Kidokezo

Tumia formula ya thamani ya wastani (Equation\ ref {averagevalue}), na utumie jiometri kutathmini muhimu.

Jibu

\(3\)

Dhana muhimu

• Muhimu wa uhakika unaweza kutumika kuhesabu eneo lililosainiwa wavu, ambalo ni eneo la juu ya\(x\) -axis chini ya eneo chini ya\(x\) -axis. Eneo lililosainiwa linaweza kuwa chanya, hasi, au sifuri.
• Sehemu ya sehemu ya muhimu ya uhakika ni integrand, kutofautiana kwa ushirikiano, na mipaka ya ushirikiano.
• Kazi zinazoendelea kwenye kipindi kilichofungwa ni integrable. Kazi ambazo haziendelei bado zinaweza kuunganishwa, kulingana na hali ya discontinuities.
• Mali ya integrals uhakika inaweza kutumika kutathmini integrals.
• Eneo chini ya safu ya kazi nyingi linaweza kuhesabiwa kwa kutumia formula za kijiometri.
• Thamani ya wastani ya kazi inaweza kuhesabiwa kwa kutumia viungo vya uhakika.

Mlinganyo muhimu

• uhakika Integral

\(\displaystyle∫^b_af(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\)

• Mali ya Integral ya uhakika

\(\displaystyle∫^a_af(x)\,dx=0\)

\(\displaystyle∫^a_bf(x)\,dx=−∫^b_af(x)\,dx\)

\(\displaystyle∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx\)

\(\displaystyle∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx\)

\(\displaystyle∫^b_acf(x)\,dx=c∫^b_af(x)\,dx\), kwa mara kwa mara\(c\)

\(\displaystyle∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx\)

faharasa

thamani ya wastani ya kazi

(au thamani\(f_{ave})\) ya wastani ya kazi kwa muda inaweza kupatikana kwa kuhesabu muhimu ya kazi na kugawanya thamani hiyo kwa urefu wa muda

dhahiri muhimu

operesheni ya msingi ya calculus; eneo kati ya curve na\(x\) -axis juu ya muda fulani ni muhimu

kazi inayoweza kuunganishwa

kazi ni integrable kama kikomo kufafanua muhimu ipo; kwa maneno mengine,, kama kikomo cha Riemann kiasi kama\(n\) inakwenda infinity ipo

umoja

kazi kwa haki ya ishara ya ushirikiano; integrand inajumuisha kazi inayounganishwa

mipaka ya ushirikiano

maadili haya yanaonekana karibu na juu na chini ya ishara muhimu na kufafanua muda ambao kazi inapaswa kuunganishwa

eneo lililosainiwa wavu

eneo kati ya kazi na\(x\) -axis kama eneo chini ya\(x\) -axis hutolewa kutoka eneo la juu\(x\) -axis; matokeo ni sawa na muhimu ya kazi

jumla ya eneo

jumla ya eneo kati ya kazi na\(x\) -axis ni mahesabu kwa kuongeza eneo juu ya\(x\) -axis na eneo chini ya\(x\) -axis; matokeo ni sawa na muhimu ya uhakika ya thamani kamili ya kazi

kutofautiana ya ushirikiano

inaonyesha ni tofauti gani unayounganisha kwa heshima; ikiwa ni\(x\), basi kazi katika integrand inafuatiwa na\(dx\)