5.1E: Mazoezi ya Sehemu ya 5.1

Last updated
Save as PDF

Page ID: 178515

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1.) Eleza kama kiasi kilichopewa ni sawa au zisizo sawa.

$\displaystyle \sum_{i=1}^{10}i$na$\displaystyle \sum_{k=1}^{10}k$
$\displaystyle \sum_{i=1}^{10}i$na$\displaystyle \sum_{i=6}^{15}(i−5)$
$\displaystyle \sum_{i=1}^{10}i(i−1)$na$\displaystyle \sum_{j=0}^9(j+1)j$
$\displaystyle \sum_{i=1}^{10}i(i−1)$na$\displaystyle \sum_{k=1}^{10}(k^2−k)$

Jibu: a. Wao ni sawa; wote kuwakilisha jumla ya kwanza 10 namba nzima.
b Wao ni sawa; wote wawili wanawakilisha jumla ya namba 10 za kwanza.
c Wao ni sawa na kubadili$\displaystyle j=i−1.$
d Wao ni sawa; jumla ya kwanza inaelezea masharti ya pili.

Katika mazoezi ya 2 - 3, tumia sheria kwa kiasi cha nguvu za integers ili kuhesabu kiasi.

2)$\displaystyle \sum_{i=5}^{10}i$

3)$\displaystyle \sum_{i=5}^{10}i^2$

Jibu: $\displaystyle \sum_{i=5}^{10}i^2 = 385−30=355$

Tuseme kwamba$\displaystyle \sum_{i=1}^{100}a_i=15$ na$\displaystyle \sum_{i=1}^{100}b_i=−12.$

Katika mazoezi 4 - 7, compute kiasi.

4)$\displaystyle \sum_{i=1}^{100}(a_i+b_i)$

5)$\displaystyle \sum_{i=1}^{100}(a_i−b_i)$

Jibu: $\displaystyle \sum_{i=1}^{100}(a_i−b_i) = 15−(−12)=27$

6)$\displaystyle \sum_{i=1}^{100}(3a_i−4b_i)$

7)$\displaystyle \sum_{i=1}^{100}(5a_i+4b_i)$

Jibu: $\displaystyle \sum_{i=1}^{100}(5a_i+4b_i) = 5(15)+4(−12)=27$

Katika mazoezi 8 - 11, tumia mali ya muhtasari na fomu ili uandike upya na kutathmini kiasi.

8)$\displaystyle \sum_{k=1}^{20}100(k^2−5k+1)$

9)$\displaystyle \sum_{j=1}^{50}(j^2−2j)$

Jibu: $\displaystyle \sum_{j=1}^{50}j^2−2\sum_{j=1}^{50}j=\frac{(50)(51)(101)}{6}−\frac{2(50)(51)}{2}=40, 375$

10)$\displaystyle \sum_{j=11}^{20}(j^2−10j)$

11)$\displaystyle \sum_{k=1}^{25}[(2k)^2−100k]$

Jibu: $\displaystyle 4\sum_{k=1}^{25}k^2−100\sum_{k=1}^{25}k=\frac{4(25)(26)(51)}{9}−50(25)(26)=−10, 400$

Hebu$L_n$ kuashiria jumla ya kushoto-mwisho kwa kutumia n subinternations na basi$R_n$ kuashiria sambamba haki-mwisho jumla.

Katika mazoezi 12 - 19, futa kiasi cha kushoto na cha kulia kilichoonyeshwa kwa kazi zilizotolewa kwenye muda ulioonyeshwa.

12)$L_4$ kwa ajili$ f(x)=\dfrac{1}{x−1}$ ya$ [2,3]$

13)$ R_4$ kwa ajili$ g(x)=\cos(πx)$ ya$ [0,1]$

Jibu: $R_4=0.25$

14)$ L_6$ kwa ajili$ f(x)=\dfrac{1}{x(x−1)}$ ya$ [2,5]$

15)$ R_6$ kwa ajili$ f(x)=\dfrac{1}{x(x−1)}$ ya$ [2,5]$

Jibu: $ R_6=0.372$

16)$ R_4$ kwa ajili$ \dfrac{1}{x^2+1}$ ya$ [−2,2]$

17)$ L_4$ kwa ajili$ \dfrac{1}{x^2+1}$ ya$ [−2,2]$

Jibu: $ L_4=2.20$

18)$ R_4$ kwa ajili$ x^2−2x+1$ ya$ [0,2]$

19)$ L_8$ kwa ajili$ x^2−2x+1$ ya$ [0,2]$

Jibu: $ L_8=0.6875$

20) Compute kushoto na kulia Riemann sums -$ L_4$ na$ R_4$, kwa mtiririko huo - kwa ajili ya$ f(x)=(2−|x|)$$ [−2,2].$ kukokotoa thamani yao wastani na kulinganisha na eneo chini ya graph ya$f$.

21) Compute kushoto na kulia Riemann sums -$ L_6$ na$ R_6$, kwa mtiririko huo - kwa ajili ya$ f(x)=(3−|3−x|)$$ [0,6].$ kukokotoa thamani yao wastani na kulinganisha na eneo chini ya graph ya$f$.

Jibu: $ L_6=9.000=R_6$. Grafu ya$f$ ni pembetatu na eneo$9\,\text{units}^2$.

22) Compute kushoto na kulia Riemann sums -$ L_4$ na$ R_4$, kwa mtiririko huo - kwa ajili ya$ f(x)=\sqrt{4−x^2}$ juu$ [−2,2]$ na kulinganisha maadili yao.

23) Compute kushoto na kulia Riemann sums -$ L_6$ na$ R_6$, kwa mtiririko huo - kwa ajili ya$ f(x)=\sqrt{9−(x−3)^2}$ juu$ [0,6]$ na kulinganisha maadili yao.

Jibu: $L_6=13.12899=R_6$. Wao ni sawa.

Kwa mazoezi 24 - 27, onyesha jumla ya mwisho ya mwisho katika alama ya sigma lakini usiwaangalie.

24)$ L_{30}$ kwa ajili$ f(x)=x^2$ ya$ [1,2]$

25)$ L_{10}$ kwa ajili$ f(x)=\sqrt{4−x^2}$ ya$ [−2,2]$

Jibu: $\displaystyle L_{10}=\frac{4}{10}\sum_{i=1}^{10}\sqrt{4−(−2+4\frac{(i−1)}{10})}$

26)$ R_{20}$ kwa ajili$ f(x)=\sin x$ ya$ [0,π]$

27)$ R_{100}$ kwa ajili$\ln x$ ya$[1,e]$

Jibu: $\displaystyle R_{100}=\frac{e−1}{100}\sum_{i=1}^{100}ln(1+(e−1)\frac{i}{100})$

Katika mazoezi 28 - 33, grafu ya kazi kisha utumie calculator au programu ya kompyuta ili kutathmini kiasi cha mwisho cha kushoto na cha kulia. Ni eneo chini ya Curve kati ya jumla ya kushoto na kulia endpoint?

28) [T]$ L_{100}$ na$ R_{100}$$ y=x^2−3x+1$ kwa muda$ [−1,1]$

29) [T]$ L_{100}$ na$R_{100}$$y=x^2$ kwa muda$[0,1]$

Jibu

$alt$

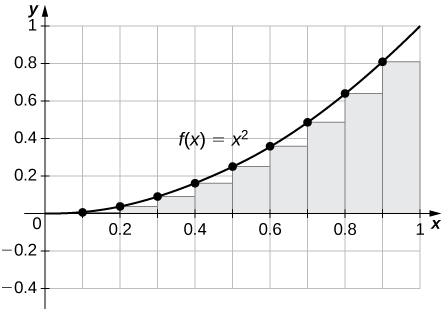
$R_{100}=0.33835,\quad L_{100}=0.32835.$
njama inaonyesha kwamba kushoto Riemann jumla ni underestimate kwa sababu kazi ni kuongezeka. Vile vile, jumla ya Riemann ya haki ni overestimate. Eneo liko kati ya jumla ya Riemann ya kushoto na ya kulia. Mstatili kumi huonyeshwa kwa uwazi wa kuona. Tabia hii inaendelea kwa rectangles zaidi.

30) [T]$L_{50}$ na$R_{50}$$y=\dfrac{x+1}{x^2−1}$ kwa muda$ [2,4]$

31) [T]$L_{100}$ na$R_{100}$$y=x^3$ kwa muda$[−1,1]$

Jibu

$alt$

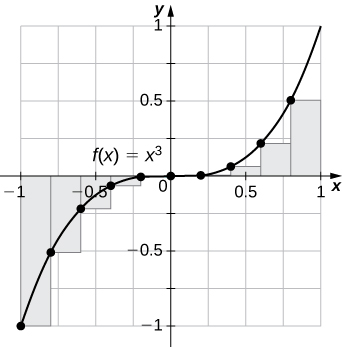
$L_{100}=−0.02,\quad R_{100}=0.02$.
Jumla ya mwisho ya kushoto ni underestimate kwa sababu kazi inaongezeka. Vile vile, haki endpoint makadirio ni overestimate. Eneo hilo liko kati ya makadirio ya mwisho ya kushoto na ya kulia.

32) [T]$L_{50}$ na$R_{50}$$y=\tan(x)$ kwa muda$[0,\frac{π}{4}]$

33) [T]$L_{100}$ na$R_{100}$$y=e^{2x}$ kwa muda$[−1,1]$

Jibu

$alt$

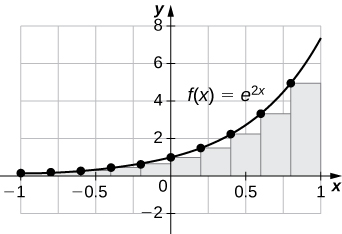
$L_{100}=3.555,\quad R_{100}=3.670$.
njama inaonyesha kwamba kushoto Riemann jumla ni underestimate kwa sababu kazi ni kuongezeka. Mstatili kumi huonyeshwa kwa uwazi wa kuona. Tabia hii inaendelea kwa rectangles zaidi.

34) Hebu$t_j$ taja wakati ambao ilichukua Tejay van Garteren kuendesha$j^\text{th}$ hatua ya Tour de France mwaka 2014. Ikiwa kulikuwa na jumla ya hatua 21, tafsiri$\displaystyle \sum_{j=1}^{21}t_j$.

35) Hebu$r_j$ taja mvua ya jumla huko Portland$j^\text{th}$ siku ya mwaka mwaka 2009. Tafsiri$\displaystyle \sum_{j=1}^{31}r_j$.

Jibu: Jumla inawakilisha mvua nyongeza katika Januari 2009.

36) Hebu$d_j$ kutaja masaa ya mchana na$ δ_j$ kuashiria ongezeko la masaa ya mchana siku$ j−1$ hadi siku$j$ huko Fargo, North Dakota,$j^\text{th}$ siku ya mwaka. Tafsiri$\displaystyle d1+\sum_{j=2}^{365}δ_j.$

37) Ili kusaidia kupata sura, Joe anapata jozi mpya ya viatu vya kukimbia. Kama Joe anaendesha 1 mi kila siku katika wiki 1 na anaongeza$\dfrac{1}{10}$ mi kwa utaratibu wake wa kila siku kila wiki, ni nini mileage jumla juu ya viatu Joe baada ya 25 wiki?

Jibu: mileage jumla ni$\displaystyle 7×\sum_{i=1}^{25}(1+\frac{(i−1)}{10})=7×25+\frac{7}{10}×12×25=385$ mi.

38) Jedwali lifuatalo linatoa maadili takriban ya kiwango cha wastani cha anga cha ongezeko la dioksidi kaboni (CO ₂) kila muongo tangu 1960, katika sehemu kwa kila milioni (ppm). Tathmini ongezeko la jumla la CO ₂ ya anga kati ya 1964 na 2013.

Muongo	ppm/y
1964-1973	1.07
1976-1983	1.34
1984-1993	1.40
1994-2003	1.87
2004-2013	2.07

Wastani wa Mwaka Anga CO2 Ongezeko, 1964—2013 Chanzo: http://www.esrl.noaa.gov/gmd/ccgg/trends/.

39) Jedwali lifuatalo linatoa ongezeko la takriban katika kiwango cha bahari kwa inchi zaidi ya miaka 20 kuanzia mwaka uliopewa. Tathmini ya mabadiliko ya wavu katika kiwango cha bahari wastani kutoka 1870 hadi 2010.

Kuanzia Mwaka	Mabadiliko ya Mwaka wa 20
1870	0.3
1890	1.5
1910	0.2
1930	2.8
1950	0.7
1970	1.1
1990	1.5

Kuongezeka kwa kiwango cha Bahari cha Miaka 20, 1870—1990

Chanzo: http://link.springer.com/article/10....712-011-9119-1

Jibu: Ongeza namba ili kupata 8.1-katika. ongezeko la wavu.

40) Jedwali lifuatalo linatoa ongezeko la takriban kwa dola kwa bei ya wastani ya lita ya gesi kwa muongo mmoja tangu 1950. Ikiwa bei ya wastani ya lita ya gesi mwaka 2010 ilikuwa $2.60, bei ya wastani ya lita ya gesi mwaka 1950 ilikuwa nini?

Kuanzia Mwaka	Mabadiliko ya Mwaka wa 10
1950	0.03
1960	0.05
1970	0.86
1980	-0.03
1990	0.29
2000	1.12

Bei ya Gesi ya Miaka 10 Kuongezeka, 1950—2000

Chanzo: epb.lbl.gov/Homepages/Rick_di... 011-trends.pdf.

41) Jedwali lifuatalo linatoa ukuaji wa asilimia ya idadi ya watu wa Marekani kuanzia Julai mwaka unahitajika. Kama idadi ya watu wa Marekani ilikuwa 281,421,906 Julai 2000, makisio ya idadi ya watu Marekani katika Julai 2010.

Mwaka	% Mabadiliko/Mwaka
2000	1.12
2001	0.99
2002	0.93
2003	0.86
2004	0.93
2005	0.93
2006	0.97
2007	0.96
2008	0.95
2009	0.88

Ukuaji wa Asilimia ya Mwaka wa Idadi ya Watu wa Marekani, 2000—2009

chanzo: www.census.gov/popest/data.

(Kidokezo: Ili kupata idadi ya watu mwezi Julai 2001, kuzidisha idadi ya watu mwezi Julai 2000 na 1.0112 kupata 284,573,831.)

Jibu: 309,389,957

Katika mazoezi 42 - 45, makadirio ya maeneo chini ya curves kwa kompyuta Riemann jumla ya kushoto,$L_8.$

42)

$alt$

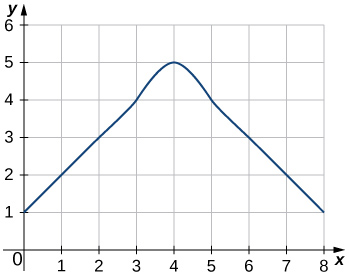
43)

$alt$

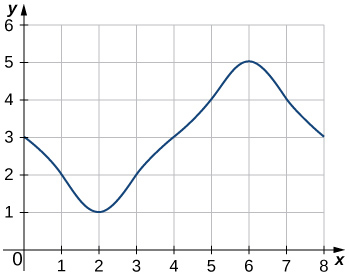
Jibu: $L_8=3+2+1+2+3+4+5+4=24$

44)

$alt$

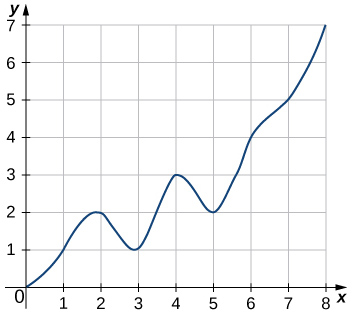
45)

$alt$

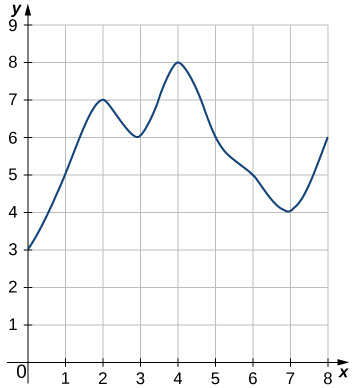
Jibu: $L_8=3+5+7+6+8+6+5+4=44$

46) [T] Tumia mfumo wa algebra ya kompyuta kukokotoa jumla ya Riemann$ L_N$,, kwa$ N=10,30,50$ ajili$ f(x)=\sqrt{1−x^2}$ ya$[−1,1].$

47) [T] Tumia mfumo wa algebra ya kompyuta kukokotoa jumla ya Riemann$L_N$,, kwa$N=10,30,50$ ajili$f(x)=\dfrac{1}{\sqrt{1+x^2}}$ ya$[−1,1].$

Jibu: $L_{10}≈1.7604,\quad L_{30}≈1.7625,\quad L_{50}≈1.76265$

48) [T] Tumia mfumo wa algebra ya kompyuta kukokotoa jumla ya Riemann$L_N$,,$N=10,30,50$ kwa ajili$f(x)=\sin^2 x$ ya$ [0,2π]$. Linganisha makadirio haya na$π$.

Katika mazoezi 49-50, tumia calculator au programu ya kompyuta ili kutathmini kiasi cha mwisho$R_N$ na$L_N$ kwa$N=1,10,100$. Je, makadirio haya yanalinganishaje na majibu halisi, ambayo unaweza kupata kupitia jiometri?

49) [T]$y=\cos(πx)$ juu ya muda$[0,1]$

Jibu: $R_1=−1,\quad L_1=1,$
$R_{10}=−0.1,\quad L_{10}=0.1,$
$L_{100}=0.01,\quad R_{100}=−0.01.$
Kwa ulinganifu wa grafu, eneo halisi ni sifuri.

50) [T]$y=3x+2$ juu ya muda$[3,5]$

Katika mazoezi 51 - 52, tumia calculator au programu ya kompyuta ili kutathmini kiasi cha mwisho$R_N$ na$L_N$$N=1,10,100.$

51) [T]$y=x^4−5x^2+4$ juu ya muda$[−2,2]$, ambayo ina eneo halisi ya$\frac{32}{15}$

Jibu: $R_1=0,\quad L_1=0,$
$R_{10}=2.4499,\quad L_{10}=2.4499,$
$R_{100}=2.1365,\quad L_{100}=2.1365$

52) [T]$y=\ln x$ juu ya muda$[1,2]$, ambayo ina eneo halisi ya$2\ln(2)−1$

53) Eleza kwa nini, ikiwa$f(a)≥0$ na$f$ inaongezeka$[a,b]$, kwamba makadirio ya mwisho ya kushoto ni ya chini ya kufungwa kwa eneo chini ya grafu ya$f$ juu$ [a,b].$

Jibu: Ikiwa$[c,d]$ ni subinterval ya$ [a,b]$ chini ya moja ya mstatili wa mwisho wa kushoto, basi eneo la mstatili linalochangia makadirio ya mwisho ya kushoto ni$ f(c)(d−c)$. Lakini,$f(c)≤f(x)$ kwa$c≤x≤d$, hivyo eneo chini ya grafu ya$f$ kati$c$ na$d$ ni$f(c)(d−c)$ pamoja na eneo chini ya grafu ya$f$ lakini juu ya sehemu ya mstari usawa kwa urefu$f(c)$, ambayo ni chanya. Kwa kuwa hii ni kweli kwa kila muda wa kushoto wa mwisho wa mwisho, inafuata kwamba jumla ya Riemann ya kushoto ni chini ya au sawa na eneo chini ya grafu ya$f$ juu$[a,b].$

54) Eleza kwa nini, ikiwa$f(b)≥0$ na f inapungua kwa$ [a,b],$ kuwa makadirio ya mwisho ya kushoto ni ya juu iliyofungwa kwa eneo chini ya grafu ya$f$ juu$ [a,b].$

55) Onyesha kwamba, kwa ujumla,$ R_N−L_N=(b−a)×\dfrac{f(b)−f(a)}{N}.$

Jibu: $\displaystyle L_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i−1}{N})=\frac{b−a}{N}\sum_{i=0}^{N−1}f(a+(b−a)\frac{i}{N})$na$\displaystyle R_N=\frac{b−a}{N}\sum_{i=1}^Nf(a+(b−a)\frac{i}{N})$. Jumla ya kushoto ina neno linalofanana$i=0$ na na jumla ya haki ina neno linalofanana na$i=N$. Katika$R_N−L_N$, neno lolote$i=1,2,…,N−1$ linalohusiana na hutokea mara moja na ishara ya pamoja na mara moja na ishara ndogo, hivyo kila neno hilo linafuta na moja imesalia$R_N−L_N=\dfrac{b−a}{N}(f(a+(b−a))\dfrac{N}{N})−(f(a)+(b−a)\dfrac{0}{N})=\dfrac{b−a}{N}(f(b)−f(a)).$

56) Eleza kwa nini, ikiwa$f$ inaongezeka$[a,b]$, kosa kati ya ama$L_N$ au$R_N$ eneo$A$ chini ya grafu ya$f$ ni zaidi$(b−a)\dfrac{f(b)−f(a)}{N}$.

57) Kwa kila moja ya grafu tatu:

Kupata chini amefungwa$L(A)$ kwa eneo iliyoambatanishwa na Curve kwa kuongeza maeneo ya mraba iliyoambatanishwa kabisa na Curve.

b Kupata juu amefungwa$U(A)$ kwa eneo hilo kwa kuongeza maeneo$L(A)$$B(A)$ ya mraba iliyoambatanishwa sehemu na Curve.

$alt$

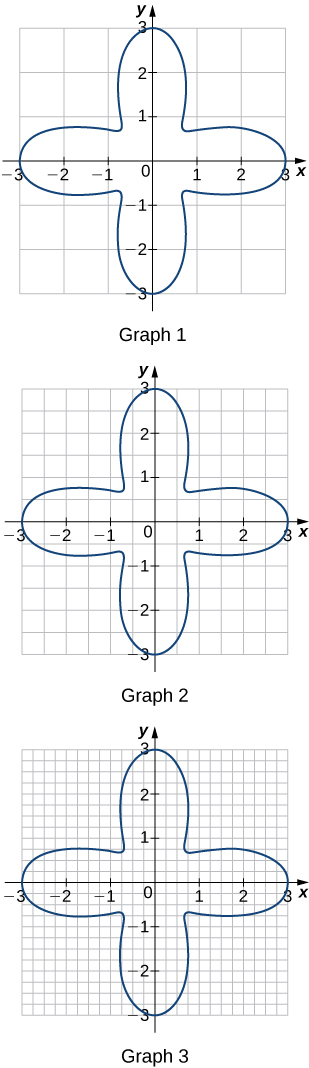
Jibu: Grafu 1: a.$L(A)=0,\quad B(A)=20; \quad b. U(A)=20.$
grafu 2:$a. L(A)=9; \quad b. B(A)=11,\quad U(A)=20.$
Grafu 3: a.$ L(A)=11.0; \quad b. B(A)=4.5,\quad U(A)=15.5.$

58) Katika zoezi la awali, kueleza kwa nini$ L(A)$ anapata hakuna ndogo wakati$U(A)$ anapata hakuna kubwa kama mraba imegawanywa katika masanduku manne ya eneo sawa.

59) Mduara wa kitengo unajumuisha n wedges sawa na kabari ya ndani katika takwimu. Msingi wa pembetatu ya ndani ni kitengo 1 na urefu wake ni$\sin(\frac{π}{n}).$ Msingi wa pembetatu ya nje ni$B=\cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n})$ na urefu ni$H=B\sin(\frac{2π}{n})$. Tumia habari hii kusema kuwa eneo la mduara wa kitengo ni sawa na$π.$

$alt$

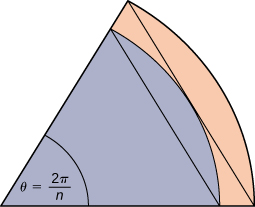
Jibu: Hebu$A$ iwe eneo la mduara wa kitengo. Mzunguko$n$ unazunguka pembetatu zenye usawa kila eneo$\dfrac{\sin(\dfrac{2π}{n})}{2}$, hivyo$\frac{n}{2}\sin(\frac{2π}{n})≤A.$ Vile vile, mduara$n$ umetokana ndani ya pembetatu zenye usawa kila eneo$\dfrac{BH}{2}=\frac{1}{2}(\cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n}))\sin(\frac{2π}{n})$, hivyo$ A≤\frac{n}{2}\sin(\frac{2π}{n})(\cos(\frac{π}{n}))+\sin(\frac{π}{n})\tan(\frac{π}{n})$. Kama$n→∞,\quad \frac{n}{2}\sin(\frac{2π}{n})=\frac{π\sin(\frac{2π}{n})}{(\frac{2π}{n})}→π$, hivyo sisi kuhitimisha$π≤A$. pia, kama$ n→∞,\quad \cos(\frac{π}{n})+\sin(\frac{π}{n})\tan(\frac{π}{n})→1$, hivyo sisi pia kuwa$A≤π$. Kwa theorem itapunguza kwa mipaka, tunahitimisha kuwa$A=π.$