5.1: Makadirio ya Maeneo

Last updated
Save as PDF

Page ID: 178492

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Tumia alama ya sigma (summation) kuhesabu kiasi na nguvu za integers.
Tumia jumla ya maeneo ya mstatili ili takriban eneo chini ya pembe.
Tumia kiasi cha Riemann kwa eneo takriban.

Archimedes alivutiwa na kuhesabu maeneo ya maumbo mbalimbali—kwa maneno mengine, kiasi cha nafasi iliyoambatanishwa na sura. Alitumia mchakato ambao umekuja kujulikana kama njia ya uchovu, ambayo ilitumia maumbo madogo na madogo, maeneo ambayo yanaweza kuhesabiwa hasa, kujaza kanda isiyo ya kawaida na hivyo kupata makadirio ya karibu na karibu na eneo la jumla. Katika mchakato huu, eneo lililofungwa na curves linajazwa na rectangles, pembetatu, na maumbo na fomu halisi za eneo. Maeneo haya ni kisha inaongozwa kwa takriban eneo la mkoa wa pembe.

Katika sehemu hii, sisi kuendeleza mbinu ya takriban eneo kati ya Curve, defined na kazi$f(x),$ na x-mhimili juu ya muda imefungwa$[a,b].$ Kama Archimedes, sisi kwanza takriban eneo chini ya Curve kutumia maumbo ya eneo inayojulikana (yaani, rectangles). Kwa kutumia rectangles ndogo na ndogo, tunapata karibu na karibu na eneo hilo. Kuchukua kikomo inatuwezesha kuhesabu eneo halisi chini ya pembe.

Hebu tuanze kwa kuanzisha notation fulani ili kufanya mahesabu iwe rahisi. Sisi kisha kuzingatia kesi wakati$f(x)$ ni kuendelea na nonnegative. Baadaye katika sura hiyo, tunapumzika baadhi ya vikwazo hivi na kuendeleza mbinu zinazotumika katika kesi zaidi.

Sigma (muhtasari) Nukuu

Kama ilivyoelezwa, tutatumia maumbo ya eneo linalojulikana ili takriban eneo la mkoa usio na kawaida unaofungwa na curves. Utaratibu huu mara nyingi unahitaji kuongeza masharti ya muda mrefu ya namba. Ili iwe rahisi kuandika kiasi hiki cha muda mrefu, tunaangalia nukuu mpya hapa, inayoitwa sigma notation (pia inajulikana kama nukuu ya summation). Barua kuu ya Kigiriki$Σ$, sigma, hutumiwa kuelezea kiasi cha maadili ya muda mrefu katika fomu ya compact. Kwa mfano, ikiwa tunataka kuongeza integers zote kutoka 1 hadi 20 bila alama ya sigma, tunapaswa kuandika

\[1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20. \nonumber \]

Tunaweza pengine kuruka kuandika maneno kadhaa na kuandika

\[1+2+3+4+⋯+19+20, \nonumber \]

ambayo ni bora, lakini bado mbaya. Kwa alama ya sigma, tunaandika jumla hii kama

\[\sum_{i=1}^{20}i \nonumber \]

ambayo ni zaidi kompakt. Kwa kawaida, ishara ya sigma imewasilishwa kwa fomu

\[\sum_{i=1}^{n}a_i \nonumber \]

ambapo$a_i$ inaeleza maneno ya kuongezwa, na$i$ inaitwa$index$. Kila neno ni tathmini, basi sisi jumla maadili yote, kuanzia na thamani wakati$i=1$ na kuishia na thamani wakati$i=n.$ Kwa mfano, kujieleza kama$\displaystyle \sum_{i=2}^{7}s_i$ ni kufasiriwa kama$s_2+s_3+s_4+s_5+s_6+s_7$. Kumbuka kuwa index hutumiwa tu kuweka wimbo wa masharti ya kuongezwa; haina sababu katika hesabu ya jumla yenyewe. Kwa hiyo index inaitwa variable dummy. Tunaweza kutumia barua yoyote tunayopenda kwa ripoti. Kwa kawaida, wanahisabati hutumia$i, \,j, \,k, \,m$, na$n$ kwa fahirisi.

Hebu jaribu mifano michache ya kutumia alama ya sigma.

Mfano$\PageIndex{1}$: Using Sigma Notation

Andika katika alama ya sigma na tathmini jumla$3^i$ ya masharti$i=1,2,3,4,5.$
Andika jumla katika alama ya sigma:

\[1+\dfrac{1}{4}+\dfrac{1}{9}+\dfrac{1}{16}+\dfrac{1}{25}. \nonumber \]

Suluhisho

Andika\[\sum_{i=1}^{5}3^i=3+3^2+3^3+3^4+3^5=363. \nonumber \]
Denominator ya kila neno ni mraba kamilifu. Kwa kutumia sigma nukuu, jumla hii inaweza kuandikwa kama$\displaystyle \sum_{i=1}^5\dfrac{1}{i^2}$.

Zoezi$\PageIndex{1}$

Andika katika alama ya sigma na tathmini jumla$2^i$ ya masharti$i=3,4,5,6.$

Kidokezo: Tumia hatua za kutatua katika Mfano$\PageIndex{1}$ kama mwongozo.

Jibu: $\displaystyle \sum_{i=3}^{6}2^i=2^3+2^4+2^5+2^6=120$

Mali zinazohusiana na mchakato wa muhtasari hutolewa katika sheria ifuatayo.

Kanuni: Mali ya Sigma Notation

Hebu$a_1,a_2,…,a_n$ na$b_1,b_2,…,b_n$ uwakilisha utaratibu wa maneno mawili na uache$c$ kuwa mara kwa mara. Mali zifuatazo zinashikilia integers zote nzuri$n$ na kwa integers$m$, na$1≤m≤n.$

$\displaystyle \sum_{i=1}^n c=nc$
$\displaystyle \sum_{i=1}^n ca_i=c\sum_{i=1}^na_i$
$\displaystyle \sum_{i=1}^n(a_i+b_i)=\sum_{i=1}^na_i+\sum_{i=1}^nb_i$
$\displaystyle \sum_{i=1}^n(a_i−b_i)=\sum_{i=1}^na_i−\sum_{i=1}^nb_i$
$\displaystyle \sum_{i=1}^na_i=\sum_{i=1}^ma_i+\sum_{i=m+1}^na_i$

Ushahidi

Sisi kuthibitisha mali (ii.) na (iii.) hapa, na kuacha ushahidi wa mali nyingine kwa Mazoezi.

(ii.) Tuna

\[\sum_{i=1}^nca_i=ca_1+ca_2+ca_3+⋯+ca_n=c(a_1+a_2+a_3+⋯+a_n)=c\sum_{i=1}^na_i. \nonumber \]

(iii.) Tuna

\[ \begin{align} \sum_{i=1}^{n}(a_i+b_i) &=(a_1+b_1)+(a_2+b_2)+(a_3+b_3)+⋯+(a_n+b_n) \\[4pt] &=(a_1+a_2+a_3+⋯+a_n)+(b_1+b_2+b_3+⋯+b_n) \\[4pt] &=\sum_{i=1}^na_i+\sum_{i=1}^nb_i. \end {align} \nonumber \]

□

Njia chache zaidi za kazi zilizopatikana mara kwa mara zinawezesha mchakato wa summation zaidi. Hizi zinaonyeshwa katika utawala unaofuata, kwa kiasi na nguvu za integers, na tunazitumia katika seti inayofuata ya mifano.

Kanuni: Sums na Mamlaka ya Integers

1. Jumla ya$n$ integers hutolewa na

\[\sum_{i=1}^n i=1+2+⋯+n=\dfrac{n(n+1)}{2}. \label{sum1} \]

2. Jumla ya integers mfululizo squared hutolewa na

\[\sum_{i=1}^n i^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6}. \label{sum2} \]

3. Jumla ya integers mfululizo cubed hutolewa na

\[\sum_{i=1}^n i^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4}. \label{sum3} \]

Mfano$\PageIndex{2}$: Evaluation Using Sigma Notation

Andika kwa kutumia alama ya sigma na tathmini:

Jumla ya masharti$(i−3)^2$ ya$i=1,2,…,200.$
Jumla ya masharti$(i^3−i^2)$ ya$i=1,2,3,4,5,6$

Suluhisho

Kuzidisha nje$(i−3)^2$, tunaweza kuvunja maneno katika maneno matatu.

\ [kuanza {align*}\ sum_ {i = 1} ^ {200} (i-3) ^2 &=\ sum_ {i = 1} ^ {200} (i ^ 2,16i+9)\\ [4pt]
&=\ sum_ {i = 1} ^ {200} i ^ {200} i=1} ^ {200} 9\\ [4pt]
&=\ sum_ {i = 1} ^ {200} i ^ 2,16\ sum_ {i = 1} ^ {200} i+\ sum_ {i = 1} ^ {200} 9\\ [4pt]
&=\ dfrac {200 (200+1) (400+1)} {6} -6\ kushoto [\ dfrac {200 (200+1)} {2}\ haki] +9 (200)\\ [4pt]
&=2,686,700-120,600+1800\\ [4pt]
&=2,567,900\ mwisho {align*}\]

b Tumia sigma notation mali iv. na sheria za jumla ya masharti ya mraba na jumla ya masharti ya cubed.

\ [kuanza {align*}\ sum_ {i = 1} ^ {6} (i ^ 3—i ^ 2) &=\ sum_ {i = 1} ^6 i ^ 3-\ sum_ {i =1} ^6 i ^ 2\\ [4pt]
&=\ dfrac {6 ^ 2 (6+1) ^2} {4} ≈\ DFRAC {6 (6+1) ^2} {4}}\ dfrac {6 (6+1)) (2 (6) +1)} {6}\ [4pt]
&=\ dfrac {1764} {4} -\ dfrac {546} {6}\\ [4pt]
&=350\ mwisho {align*}\ namba\]

Zoezi$\PageIndex{2}$

Pata jumla ya maadili ya$4+3i$ kwa$i=1,2,…,100.$

Kidokezo: Tumia mali ya alama ya sigma ili kutatua tatizo.

Jibu: $15,550$

Mfano$\PageIndex{3}$: Finding the Sum of the Function Values

Pata jumla ya maadili ya$f(x)=x^3$ zaidi ya integers$1,2,3,…,10.$

Suluhisho

Kutumia Equation\ ref {sum3}, tuna

\[\sum_{i=0}^{10}i^3=\dfrac{(10)^2(10+1)^2}{4}=\dfrac{100(121)}{4}=3025 \nonumber \]

Zoezi$\PageIndex{3}$

Tathmini jumla iliyoonyeshwa na notation$\displaystyle \sum_{k=1}^{20}(2k+1)$.

Kidokezo: Tumia utawala juu ya jumla na nguvu za integers (Equations\ ref {sum1} -\ ref {sum3}).

Jibu: $440$

Kukadiria Area

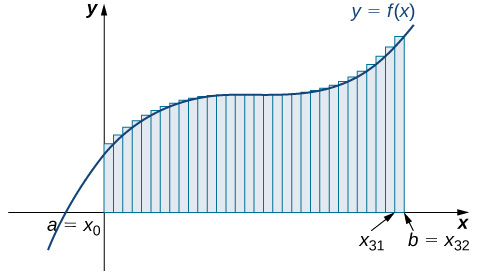
Sasa kwa kuwa tuna alama muhimu, tunarudi tatizo lililopo: kukadiria eneo chini ya pembe. Hebu$f(x)$ iwe kazi inayoendelea, isiyo ya hasi iliyofafanuliwa kwenye muda uliofungwa$[a,b]$. Tunataka takriban eneo$A$ lililofungwa na$f(x)$ hapo juu,$x$ -axis chini, mstari$x=a$ upande wa kushoto, na mstari$x=b$ wa kulia (Kielelezo$\PageIndex{1}$).

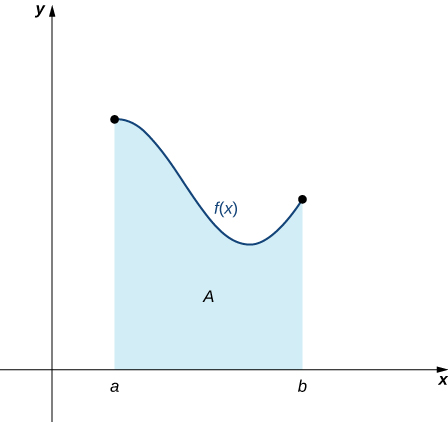
Grafu katika roboduara moja ya eneo lililofungwa na safu ya generic f (x) hapo juu, x-axis chini, mstari x = a upande wa kushoto, na mstari x = b kwa haki. Kuhusu katikati ya njia, concavity inachukua kutoka concave chini hadi concave up, na kazi huanza kuongezeka muda mfupi kabla ya mstari x = b. — Kielelezo$\PageIndex{1}$: Eneo (kivuli kanda) imepakana na$f(x)$ Curve juu,$x$ -axis chini, mstari$x=a$ wa kushoto, na mstari$x=b$ wa kulia.

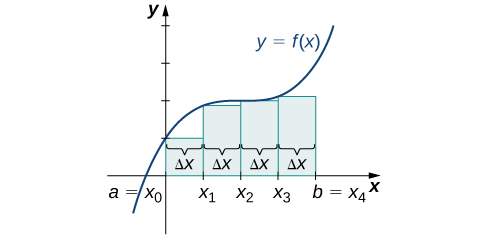
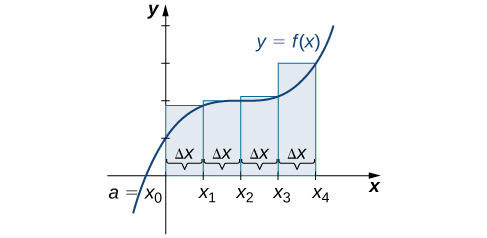
Je, sisi takriban eneo chini ya curve hii? Njia hiyo ni moja ya kijiometri. Kwa kugawa kanda katika maumbo mengi madogo ambayo yanajulikana eneo formula, tunaweza kuhesabu maeneo haya na kupata makadirio ya kuridhisha ya eneo la kweli. Tunaanza kwa kugawanya muda$[a,b]$ katika$n$ sehemu ndogo za upana sawa,$\dfrac{b−a}{n}$. Tunafanya hivyo kwa kuchagua pointi sawa na spaced$x_0,x_1,x_2,…,x_n$$x_0=a,x_n=b,$ na

\[x_i−x_{i−1}=\dfrac{b−a}{n} \nonumber \]

kwa$i=1,2,3,…,n.$

Tunaashiria upana wa kila subinterval na notation$Δx,$ hivyo$Δx=\frac{b−a}{n}$ na

\[x_i=x_0+iΔx \nonumber \]

kwa$i=1,2,3,…,n.$ Dhana hii ya kugawanya muda$[a,b]$ katika sehemu ndogo kwa kuchagua pointi kutoka ndani ya muda hutumiwa mara nyingi kabisa katika kukadiria eneo chini ya pembe, basi hebu tufafanue istilahi husika.

Ufafanuzi: Sehemu

Seti ya pointi$P={x_i}$ kwa$i=0,1,2,…,n$ na$a=x_0 < x_1 < x_2 < ... < x_n = b$, ambayo hugawanya muda$[a, b]$ katika sehemu ndogo ya fomu$[x_0, x_1], [x_1, x_2], ..., [x_{n-1}, x_n]$ inaitwaugawaji wa$[a,b]$. Ikiwa vipindi vyote vina upana sawa, seti ya pointi huunda sehemu ya kawaida (au ugawaji wa sare) wa muda$[a,b].$

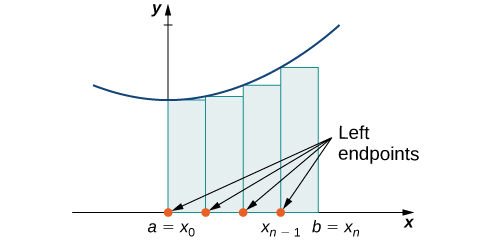
Tunaweza kutumia kizigeu hiki cha kawaida kama msingi wa njia ya kukadiria eneo chini ya pembe. Sisi ijayo kuchunguza mbinu mbili: kushoto-mwisho makadirio na haki-mwisho makadirio.

Kanuni: Upimaji wa mwisho wa kushoto

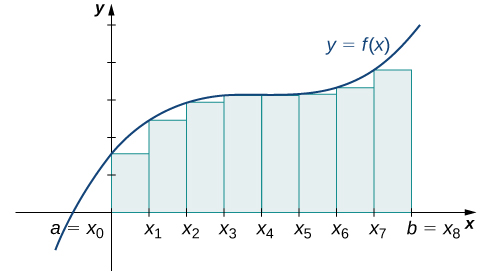
Kwa kila subinterval$[x_{i−1},x_i]$ (kwa$i=1,2,3,…,n$), jenga mstatili$Δx$ na upana na urefu sawa na$f(x_{i−1})$, ambayo ni thamani ya kazi kwenye mwisho wa kushoto wa subinterval. Kisha eneo la mstatili huu ni$f(x_{i−1})Δx$. Kuongeza maeneo ya rectangles hizi zote, tunapata thamani ya takriban$A$ (Kielelezo$\PageIndex{2}$). Tunatumia nukuu$L_n$ kuashiria kwamba hii ni makadirio ya kushoto-mwisho ya$A$ kutumia$n$ subspinternations.

\[A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\sum_{i=1}^nf(x_{i−1})Δx \nonumber \]

mchoro kuonyesha kushoto-mwisho makadirio ya eneo chini ya Curve. Chini ya parabola na vertex kwenye mhimili y na juu ya mhimili x, rectangles hutolewa kati ya a=x0 juu ya asili na b = xn. Mstatili una mwisho katika a=x0, x1, x2... x (n-1), na b = xn, spaced sawa. Urefu wa kila mstatili hutegemea thamani ya kazi iliyotolewa kwenye mwisho wa kushoto wa mstatili. — Kielelezo$\PageIndex{2}$: Katika makadirio ya mwisho ya kushoto ya eneo chini ya pembe, urefu wa kila mstatili hutegemea thamani ya kazi upande wa kushoto wa kila subinterval.

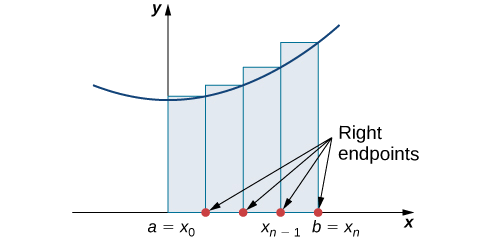
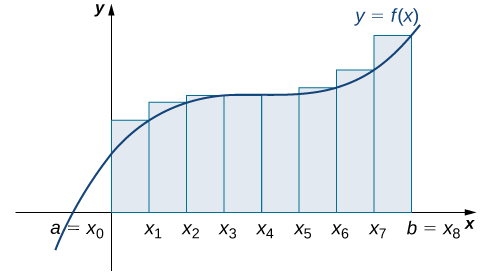
Njia ya pili kwa ajili ya makadirio ya eneo chini ya Curve ni haki-mwisho makadirio. Ni karibu sawa na makadirio ya mwisho wa kushoto, lakini sasa urefu wa rectangles hutegemea maadili ya kazi kwa haki ya kila subinterval.

Kanuni: Upimaji wa Mwisho wa Haki

Kujenga mstatili juu ya kila subinterval$[x_{i−1},x_i]$, tu wakati huu urefu wa mstatili imedhamiriwa na thamani$f(x_i)$ ya kazi kwenye mwisho wa mwisho wa subinterval. Kisha, eneo la kila mstatili ni$f(x_i)\,Δx$ na makadirio$A$ ya hutolewa na

\[A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\sum_{i=1}^nf(x_i)Δx. \nonumber \]

nukuu$R_n$ inaonyesha hii ni haki-mwisho makadirio kwa$A$ (Kielelezo$\PageIndex{3}$).

mchoro kuonyesha haki-mwisho makadirio ya eneo chini ya Curve. Chini ya parabola na vertex kwenye mhimili y na juu ya mhimili x, rectangles hutolewa kati ya a=x0 juu ya asili na b = xn. Mstatili una mwisho katika a=x0, x1, x2... x (n-1), na b = xn, spaced sawa. Urefu wa kila mstatili hutegemea thamani ya kazi iliyotolewa kwenye mwisho wa mwisho wa mstatili. — Kielelezo$\PageIndex{3}$: Katika makadirio ya mwisho ya eneo la chini ya pembe, urefu wa kila mstatili hutegemea thamani ya kazi kwa haki ya kila subinterval. Kumbuka kuwa haki-mwisho makadirio hutofautiana na kushoto-mwisho makadirio katika Kielelezo$\PageIndex{2}$.

Grafu katika Kielelezo$\PageIndex{4}$ kuwakilisha Curve$f(x)=\dfrac{x^2}{2}$. Katika Kielelezo$\PageIndex{4b}$ tunagawanya kanda iliyowakilishwa na muda$[0,3]$ katika vipindi sita, kila upana$0.5$. Hivyo,$Δx=0.5$. Kisha tunaunda mstatili sita kwa kuchora mistari ya wima perpendicular kwa$x_{i−1}$, mwisho wa kushoto wa kila subinterval. Tunaamua urefu wa kila mstatili kwa kuhesabu$f(x_{i−1})$$i=1,2,3,4,5,6.$ kwa vipindi ni$[0,0.5],[0.5,1],[1,1.5],[1.5,2],[2,2.5],[2.5,3]$. Tunapata eneo la kila mstatili kwa kuzidisha urefu kwa upana. Kisha, jumla ya maeneo ya mstatili inakaribia eneo kati$f(x)$ na$x$ -axis. Wakati endpoints kushoto ni kutumika kwa mahesabu ya urefu, tuna kushoto-mwisho makadirio. Hivyo,

\ [kuanza {align*} A≈ L_6 &=\ sum_ {i = 1} ^6f (x_ {i-1}) Δx =f (x_0) Δx+F (x_1) Δx+F (x_2) Δx+F (x_3) Δx+F (x_4) Δx+F (x_5) Δx\ [4pt]
&=f (0) 0.5+f (0.5) 0.5+f (1) 0.5+f (1.5) 0.5+f (2) 0.5+f (2.5) 0.5\\ [4pt]
& =( 0) 0.5+ (0.125) 0.5+ (0.125) 0.5+ (2) 0.5+ (3.125) 0.5\\ [4pt]
&=0+0.0625 +0.25+0.5625+1+1.5625\\ [4pt]
&=3.4375\,\ maandishi {vitengo} ^2\ mwisho {align*}\ nonumber\]

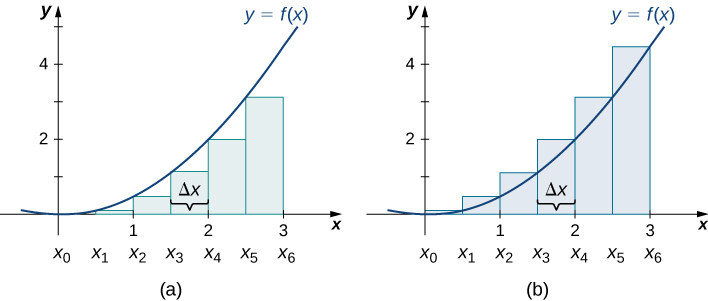
Michoro upande kwa upande, kuonyesha tofauti katika makadirio ya eneo chini ya Curve parabolic na kipeo katika asili kati ya njia ya kushoto endpoints (mchoro kwanza) na haki endpoints njia (mchoro wa pili). Katika mchoro wa kwanza, rectangles hutolewa kwa vipindi hata (delta x) chini ya pembe na urefu uliowekwa na thamani ya kazi kwenye mwisho wa kushoto. Katika mchoro wa pili, rectangles hutolewa kwa mtindo huo, lakini kwa urefu uliowekwa na thamani ya kazi kwenye mwisho wa mwisho. Mwisho wa mwisho katika wote wawili umewekwa sawa kutoka kwa asili hadi (3, 0), iliyoandikwa x0 hadi x6. — Kielelezo$\PageIndex{4}$: Njia za kukadiria eneo chini ya pembe kwa kutumia (a) mwisho wa kushoto na (b) mwisho wa kulia.

Katika Kielelezo$\PageIndex{4b}$, tunatumia mistari ya wima perpendicular kwa$x_i$ vile kwamba$x_i$ ni mwisho wa mwisho wa kila subinterval, na kuhesabu$f(x_i)$ kwa$i=1,2,3,4,5,6$. Tunazidisha kila mmoja$f(x_i)$$Δx$ ili kupata maeneo ya mstatili, na kisha uwaongeze. Hii ni haki-mwisho makadirio ya eneo chini ya$f(x)$. Hivyo,

\ [kuanza {align*} A≈ R_6 &=\ sum_ {i = 1} ^6f (x_i) Δx=F (x_1) Δx+F (x_2) Δx+F (x_3) Δx+F (x_4) Δx+F (x_5) Δx+F (x_6) Δx\\ [4pt]
&=f (0.5) 0.5+f (1) 0.5+f (1.5) 0.5+f (2) 0.5+f (2.5) 0.5+f (3) 0.5\\ [4pt]
& =( 0.125) 0.5+ (0.5) 0.5+ (1.125) 0.5+ (2) 0.5+ (3.125) 0.5+ (4.5) 0.5\\ [4pt]
&=0.0625+0.25 +0.5625+1+1.5625+2.25\\ [4pt]
&=5.6875\,\ maandishi {vitengo} ^2. \ mwisho {align*}\ nonumber\]

Mfano$\PageIndex{4}$: Approximating the Area Under a Curve

Matumizi wote kushoto-mwisho na haki-mwisho makadirio ya takriban eneo chini ya Curve ya$f(x)=x^2$ juu ya muda$[0,2]$; matumizi$n=4$.

Suluhisho

Kwanza, ugawanye muda$[0,2]$ katika sehemu ndogo$n$ sawa. Kutumia$n=4,\, Δx=\dfrac{(2−0)}{4}=0.5$. Hii ni upana wa kila mstatili. Vipindi$[0,0.5],[0.5,1],[1,1.5],[1.5,2]$ vinaonyeshwa kwenye Kielelezo$\PageIndex{5}$. Kwa kutumia kushoto-mwisho makadirio, urefu ni$f(0)=0,\,f(0.5)=0.25,\,f(1)=1,$ na$f(1.5)=2.25.$ Kisha,

\[ \begin{align*} L_4 &=f(x_0)Δx+f(x_1)Δx+f(x_2)Δx+f(x_3)Δx \\[4pt] &=0(0.5)+0.25(0.5)+1(0.5)+2.25(0.5) \\[4pt] &=1.75 \,\text{units}^2 \end{align*} \nonumber \]

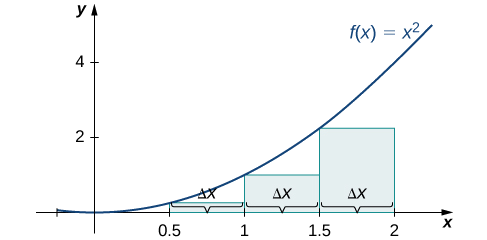
Grafu ya makadirio ya mwisho ya kushoto ya eneo chini ya pembe f (x) = x ^ 2 kutoka 0 hadi 2 na endpoints spaced vitengo .5 mbali. Urefu wa mstatili hutegemea maadili ya kazi kwenye mwisho wao wa kushoto. — Kielelezo$\PageIndex{5}$: Grafu inaonyesha makadirio ya mwisho ya kushoto ya eneo chini$f(x)=x^2$ kutoka$0$ kwa$2$.

makadirio haki-mwisho uhakika ni inavyoonekana katika Kielelezo$\PageIndex{6}$. Kipindi ni sawa,$Δx=0.5,$ lakini sasa tumia mwisho wa mwisho wa kuhesabu urefu wa rectangles. Tuna

\[ \begin{align*} R_4 &=f(x_1)Δx+f(x_2)Δx+f(x_3)Δx+f(x_4)Δx \\[4pt] &=0.25(0.5)+1(0.5)+2.25(0.5)+4(0.5) \\[4pt] &=3.75 \,\text{units}^2 \end{align*} \nonumber \]

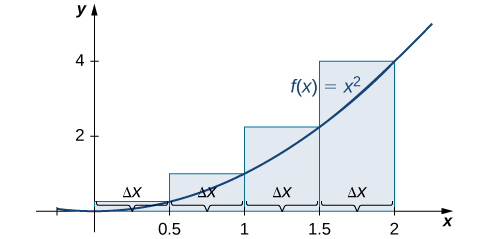
Grafu ya njia ya makadirio ya mwisho ya haki ya eneo chini ya pembe f (x) = x ^ 2 kutoka 0 hadi 2 na endpoints spaced vitengo .5 mbali. Urefu wa rectangles hutegemea maadili ya kazi kwenye mwisho wa mwisho. — Kielelezo$\PageIndex{6}$: Grafu inaonyesha makadirio ya mwisho ya haki ya eneo chini$f(x)=x^2$ kutoka$0$ kwa$2$.

kushoto-mwisho makadirio ni$1.75\,\text{units}^2$; haki-mwisho makadirio ni$3.75 \,\text{units}^2$.

Zoezi$\PageIndex{4}$

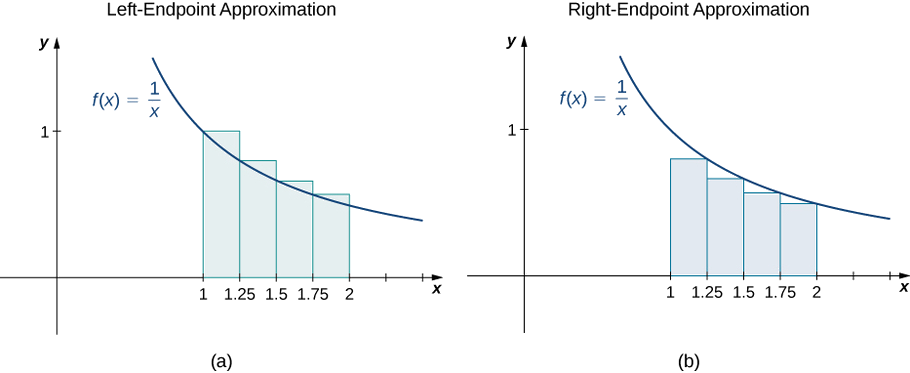
Mchoro kushoto-mwisho na haki-mwisho makadirio kwa ajili ya$f(x)=\dfrac{1}{x}$ juu ya$[1,2]$; matumizi$n=4$. Takriban eneo hilo kwa kutumia njia zote mbili.

Kidokezo: Fuata mkakati wa kutatua katika Mfano$\PageIndex{4}$ hatua kwa hatua.

Jibu

kushoto-mwisho makadirio ni$0.7595 \,\text{units}^2$. haki-mwisho makadirio ni$0.6345 \,\text{units}^2$. Angalia chini Media.

$Grafu mbili upande kwa upande kuonyesha kushoto-mwisho makadirio na haki-mwisho makadirio ya eneo chini ya Curve f (x) = 1/x kutoka 1 kwa 2 na endpoints spaced sawasawa katika .25 vitengo. Urefu wa makadirio ya mwisho wa kushoto hutambuliwa na maadili ya kazi kwenye mwisho wa kushoto, na urefu wa makadirio ya mwisho wa kulia hutegemea maadili ya kazi kwenye mwisho wa kulia.$

Kuangalia Kielelezo$\PageIndex{4}$ na grafu katika Mfano$\PageIndex{4}$, tunaweza kuona kwamba wakati sisi kutumia idadi ndogo ya vipindi, wala kushoto mwisho makadirio wala haki-mwisho makadirio ni makadirio hasa sahihi ya eneo chini ya Curve. Hata hivyo, inaonekana mantiki kwamba ikiwa tunaongeza idadi ya pointi katika ugawaji wetu, makadirio yetu ya$A$ yataboresha. Tutakuwa na rectangles zaidi, lakini kila mstatili utakuwa mwembamba, hivyo tutaweza kuunganisha rectangles kwa curve zaidi kwa usahihi.

Tunaweza kuonyesha kuboresha makadirio kupatikana kwa njia ya vipindi vidogo na mfano. Hebu tuchunguze wazo la kuongezeka$n$, kwanza katika makadirio ya mwisho ya kushoto na rectangles nne, kisha rectangles nane, na hatimaye$32$ rectangles. Kisha, hebu tufanye kitu kimoja katika makadirio ya haki-mwisho, kwa kutumia seti hiyo ya vipindi, ya mkoa huo ikiwa. Kielelezo$\PageIndex{7}$ inaonyesha eneo la kanda chini ya Curve$f(x)=(x−1)^3+4$ juu ya muda$[0,2]$ kwa kutumia kushoto-mwisho makadirio ambapo. upana$n=4.$ wa kila mstatili ni

\[Δx=\dfrac{2−0}{4}=\dfrac{1}{2}.\nonumber \]

Eneo hilo linakadiriwa na maeneo yaliyofupishwa ya rectangles, au

\[L_4=f(0)(0.5)+f(0.5)(0.5)+f(1)(0.5)+f(1.5)0.5=7.5 \,\text{units}^2\nonumber \]

Grafu ya makadirio ya mwisho ya kushoto ya eneo chini ya safu iliyotolewa kutoka = x0 kwa b=x4. Urefu wa rectangles hutegemea maadili ya kazi kwenye mwisho wa kushoto. — Kielelezo$\PageIndex{7}$: Kwa makadirio ya mwisho wa kushoto na kugawanya kanda kutoka$a$ kwa vipindi vinne sawa, eneo chini ya pembe ni takriban sawa na jumla ya maeneo ya rectangles.$b$

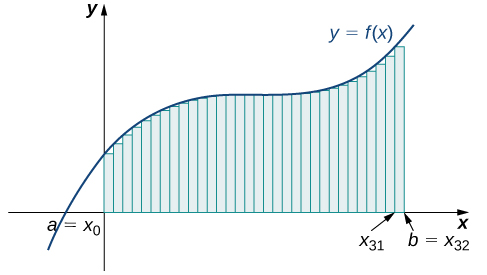
Kielelezo$\PageIndex{8}$ kinaonyesha Curve sawa imegawanywa katika subinternations nane. Kulinganisha grafu na rectangles nne katika Kielelezo$\PageIndex{7}$ na grafu hii na rectangles nane, tunaweza kuona kuna inaonekana kuwa chini nyeupe nafasi chini ya Curve wakati$n=8.$ Hii nafasi nyeupe ni eneo chini ya Curve hatuwezi ni pamoja na kutumia makadirio yetu. Eneo la rectangles ni

\[L_8=f(0)(0.25)+f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)=7.75 \,\text{units}^2\nonumber \]

Grafu inayoonyesha makadirio ya mwisho ya kushoto kwa eneo chini ya safu iliyotolewa kutoka a=x0 hadi b = x8. Urefu wa rectangles hutegemea maadili ya kazi kwenye mwisho wa kushoto. — Kielelezo$\PageIndex{8}$: Kanda chini ya Curve imegawanywa katika maeneo ya$n=8$ mstatili wa upana sawa kwa makadirio ya mwisho wa kushoto.

Grafu katika Kielelezo$\PageIndex{9}$ inaonyesha kazi sawa na$32$ rectangles iliyoandikwa chini ya safu. Inaonekana kuwa na nafasi nyeupe kidogo iliyoachwa. Eneo linalohusika na rectangles ni

\[L_{32}=f(0)(0.0625)+f(0.0625)(0.0625)+f(0.125)(0.0625)+⋯+f(1.9375)(0.0625)=7.9375 \,\text{units}^2.\nonumber \]

Grafu ya makadirio ya mwisho ya kushoto ya eneo chini ya safu iliyotolewa kutoka = x0 hadi b = x32. Urefu wa rectangles hutegemea maadili ya kazi kwenye mwisho wa kushoto. — Kielelezo$\PageIndex{9}$: Hapa,$32$ rectangles ni andikwa chini ya Curve kwa makadirio ya kushoto-mwisho.

Tunaweza kutekeleza mchakato sawa kwa njia ya makadirio ya haki-mwisho. Makadirio ya mwisho wa mwisho wa curve sawa, kwa kutumia rectangles nne (Kielelezo$\PageIndex{10}$), hutoa eneo

\[R_4=f(0.5)(0.5)+f(1)(0.5)+f(1.5)(0.5)+f(2)(0.5)=8.5 \,\text{units}^2.\nonumber \]

Grafu ya makadirio ya mwisho ya haki-mwisho kwa eneo chini ya Curve iliyotolewa kutoka x0 hadi x4. Urefu wa rectangles hutegemea maadili ya kazi kwenye mwisho wa mwisho. — Kielelezo$\PageIndex{10}$: Sasa tunagawanya eneo chini ya pembe ndani ya subinternations nne sawa kwa makadirio ya mwisho wa haki-mwisho.

Kugawanya kanda juu ya muda$[0,2]$ katika rectangles nane matokeo katika$Δx=\dfrac{2−0}{8}=0.25.$ Grafu inavyoonekana katika Kielelezo$\PageIndex{11}$. Eneo hilo ni

\[R_8=f(0.25)(0.25)+f(0.5)(0.25)+f(0.75)(0.25)+f(1)(0.25)+f(1.25)(0.25)+f(1.5)(0.25)+f(1.75)(0.25)+f(2)(0.25)=8.25 \,\text{units}^2\nonumber \]

Grafu ya makadirio ya mwisho wa kulia kwa eneo chini ya safu iliyotolewa kutoka a=x0 hadi B=x8.urefu wa rectangles hutegemea maadili ya kazi kwenye mwisho wa kulia. — Kielelezo$\PageIndex{11}$: Hapa sisi kutumia haki-mwisho makadirio kwa ajili ya mkoa umegawanyika katika subspinternations nane sawa.

Mwisho, makadirio ya mwisho ya haki na$n=32$ iko karibu na eneo halisi (Kielelezo$\PageIndex{12}$). Eneo hilo ni takriban

\[R_{32}=f(0.0625)(0.0625)+f(0.125)(0.0625)+f(0.1875)(0.0625)+⋯+f(2)(0.0625)=8.0625 \,\text{units}^2\nonumber \]

Grafu ya makadirio ya mwisho wa haki-mwisho kwa eneo chini ya safu iliyotolewa kutoka a=x0 hadi b=x32. Urefu wa rectangles hutegemea maadili ya kazi kwenye mwisho wa mwisho. — Kielelezo$\PageIndex{12}$: kanda imegawanywa katika subspinternations$32$ sawa kwa haki-mwisho makadirio.

Kulingana na takwimu hizi na mahesabu, inaonekana sisi ni juu ya kufuatilia haki; rectangles kuonekana takriban eneo chini ya Curve bora kama$n$ anapata kubwa. Zaidi ya hayo, kama$n$ ongezeko, wote kushoto-mwisho na haki-mwisho makadirio kuonekana mbinu eneo la vitengo$8$ mraba. Jedwali$\PageIndex{15}$ linaonyesha kulinganisha namba ya mbinu za kushoto na za mwisho. Wazo kwamba makadirio ya eneo chini ya Curve kupata bora na bora kama$n$ anapata kubwa na kubwa ni muhimu sana, na sasa sisi kuchunguza wazo hili kwa undani zaidi.

Jedwali$\PageIndex{15}$: Converging Maadili ya Kushoto- na Right-Endpoint makadirio kama$n$ O
Thamani ya$n$	Eneo la Takriban$L_n$	Eneo la Takriban$R_n$
\ (n\)” style="wima align:katikati; ">$n=4$	\ (L_n\)” style="wima align:katikati; ">$7.5$	\ (R_n\)” style="wima align:katikati; ">$8.5$
\ (n\)” style="wima align:katikati; ">$n=8$	\ (L_n\)” style="wima align:katikati; ">$7.75$	\ (R_n\)” style="wima align:katikati; ">$8.25$
\ (n\)” style="wima align:katikati; ">$n=32$	\ (L_n\)” style="wima align:katikati; ">$7.94$	\ (R_n\)” style="wima align:katikati; ">$8.06$

kutengeneza Riemann Sums

Hadi sasa tumekuwa tunatumia rectangles ili takriban eneo chini ya pembe. Urefu wa mstatili huu umeamua kwa kutathmini kazi kwa upande wa mwisho wa kulia au wa kushoto wa subinterval$[x_{i−1},x_i]$. Kwa kweli, hakuna sababu ya kuzuia tathmini ya kazi kwa moja ya pointi hizi mbili tu. Tunaweza kutathmini kazi wakati wowote$x^∗_i$ katika subinterval$[x_{i−1},x_i]$, na kutumia$f(x^∗_i)$ kama urefu wa mstatili wetu. Hii inatupa makadirio ya eneo la fomu

\[A≈\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]

Jumla ya fomu hii inaitwa jumla ya Riemann, jina lake kwa mwanahisabati wa karne ya 19 Bernhard Riemann, ambaye aliendeleza wazo hilo.

ufafanuzi: Riemann jumla

Hebu$f(x)$ kuelezwa juu ya muda imefungwa$[a,b]$ na basi$P$ kuwa kizigeu yoyote ya$[a,b]$. Hebu$Δx_i$ iwe upana wa kila subinterval$[x_{i−1},x_i]$ na kwa kila mmoja$i$, hebu$x^∗_i$ iwe na uhakika wowote$[x_{i−1},\,x_i]$. Jumla Riemann hufafanuliwa kwa$f(x)$ kama

\[\sum_{i=1}^nf(x^∗_i)\,Δx_i. \nonumber \]

Kwa hatua hii, tutachagua ugawaji wa kawaida$P$, kama tunavyo katika mifano yetu hapo juu. Hii$Δx_i$ inasababisha wote kuwa sawa na$Δx = \dfrac{b-a}{n}$ kwa idadi yoyote ya asili ya vipindi$n$.

Kumbuka kwamba kwa upande wa kushoto- na makadirio haki-mwisho, makadirio wanaonekana kupata bora na bora kama$n$ kupata kubwa na kubwa. Kitu kimoja kinachotokea kwa kiasi cha Riemann. Riemann kiasi kutoa makadirio bora kwa maadili kubwa ya$n$. Sisi sasa ni tayari kufafanua eneo chini ya Curve katika suala la Riemann kiasi.

Ufafanuzi: Eneo Chini ya Curve

Hebu$f(x)$ kuendelea, nonhegative kazi juu ya muda$[a,b]$, na hebu$\displaystyle \sum_{i=1}^nf(x^∗_i)\,Δx$ kuwa Riemann jumla kwa$f(x)$ kwa kuhesabu mara kwa mara$P$. Kisha, eneo chini ya Curve$y=f(x)$ juu$[a,b]$ linatolewa na

\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)\,Δx. \nonumber \]

Angalia maonyesho ya graphical ya ujenzi wa jumla ya Riemann.

Baadhi ya udanganyifu hapa ni muhimu kujadili. Kwanza, kumbuka kuwa kuchukua kikomo cha jumla ni tofauti kidogo na kuchukua kikomo cha kazi$f(x)$ kama$x$ inakwenda infinity. Mipaka ya kiasi hujadiliwa kwa undani katika sura ya Utaratibu na Mfululizo; hata hivyo, kwa sasa tunaweza kudhani kuwa mbinu za kuhesabu tulizotumia kukokotoa mipaka ya kazi pia zinaweza kutumika kuhesabu mipaka ya kiasi.

Pili, ni lazima kufikiria nini cha kufanya kama kujieleza hujiunga na mipaka tofauti kwa ajili ya uchaguzi tofauti ya${x^∗_i}.$ bahati nzuri, hii haina kutokea. Ingawa ushahidi ni zaidi ya upeo wa maandishi haya, inaweza kuonyeshwa kuwa ikiwa$f(x)$ inaendelea kwenye muda uliofungwa$[a,b]$, basi$\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx$ ipo na ni ya kipekee (kwa maneno mengine, haitegemei uchaguzi wa${x^∗_i}$).

Tunaangalia baadhi ya mifano ya muda mfupi. Lakini, kabla ya kufanya, hebu kuchukua muda na majadiliano juu ya baadhi ya uchaguzi maalum kwa ajili ya${x^∗_i}$. Ingawa uchaguzi wowote unatupa${x^∗_i}$ makadirio ya eneo chini ya pembe, hatujui kama makadirio hayo ni ya juu sana (overestimate) au chini sana (underestimate). Ikiwa ni muhimu kujua kama makadirio yetu ni ya juu au ya chini, tunaweza kuchagua thamani yetu${x^∗_i}$ ili kuhakikisha matokeo moja au nyingine.

Ikiwa tunataka overestimate, kwa mfano, tunaweza kuchagua${x^∗_i}$ vile$i=1,2,3,…,n,$$f(x^∗_i)≥f(x)$ kwa wote$x∈[x_i−1,x_i]$. Kwa maneno mengine, sisi kuchagua${x^∗_i}$ ili kwa$i=1,2,3,…,n,$$f(x^∗_i)$ ni upeo kazi thamani juu ya muda$[x_{i−1},x_i]$. Ikiwa tunachagua${x^∗_i}$ kwa njia hii, basi jumla ya Riemann$\displaystyle \sum_{i=1}^nf(x^∗_i)Δx$ inaitwa jumla ya juu. Vile vile, kama tunataka underestimate, tunaweza kuchagua${x∗i}$ ili kwa$i=1,2,3,…,n,$$f(x^∗_i)$ ni thamani ya chini ya kazi ya muda$[x_{i−1},x_i]$. Katika kesi hiyo, jumla ya Riemann inayohusishwa inaitwa jumla ya chini. Kumbuka kwamba ikiwa$f(x)$ inaongezeka au kupungua kwa muda wote$[a,b]$, basi maadili ya kiwango cha juu na cha chini ya kazi hutokea kwenye mwisho wa vipindi vya chini, hivyo kiasi cha juu na cha chini ni sawa na makadirio ya kushoto na ya mwisho.

Mfano$\PageIndex{5}$: Finding Lower and Upper Sums

Pata kiasi cha chini kwa ajili ya$f(x)=10−x^2$ juu$[1,2]$; basi$n=4$ subinternations.

Suluhisho

Na$n=4$ zaidi ya muda$[1,2], \,Δx=\dfrac{1}{4}$. Tunaweza kuorodhesha vipindi kama$[1,1.25],\,[1.25,1.5],\,[1.5,1.75],$ na$[1.75,2]$. Kwa sababu kazi ni kupungua zaidi ya muda$[1,2],$ Kielelezo inaonyesha kwamba kiasi cha chini ni kupatikana kwa kutumia endpoints haki.

Grafu ya f (x) = 10 ÷ x ^ 2 kutoka 0 hadi 2. Ni kuanzisha kwa ajili ya haki ya mwisho makadirio ya eneo imepakana na Curve na mhimili x juu ya [1, 2], kinachoitwa a=x0 kwa x4. Inaonyesha jumla ya chini. — Kielelezo$\PageIndex{13}$: graph ya$f(x)=10−x^2$ ni kuanzisha kwa haki-mwisho makadirio ya eneo imepakana na Curve na$x$ -mhimili juu ya$[1,2]$, na inaonyesha kiasi chini.

Jumla ya Riemann ni

\ [kuanza {align*}\ sum_ {k=1} ^4 (10,1x^2) (0.25) &=0.25 [10÷ (1.25) ^2+10|( 1.5) ^2+10|( 1.75) ^2+10|( 2) ^2]\\ [4pt]
&=0.25 [8.4375+7.75+6.9375+6]\\ [4pt]
&=7.28\,\ maandishi {vitengo} ^2. \ mwisho {align*}\]

Eneo la$7.28$$\text{units}^2$ ni jumla ya chini na underestimate.

Zoezi$\PageIndex{5}$

Pata jumla ya$f(x)=10−x^2$ juu kwa$[1,2]$; basi$n=4.$
Mchoro makadirio.

Kidokezo: $f(x)$inapungua$[1,2]$, hivyo maadili ya juu ya kazi hutokea kwenye mwisho wa kushoto wa vipindi.

Jibu

a Jumla ya juu=$8.0313 \,\text{units}^2.$

$Grafu ya kazi f (x) = 10 ÷ x ^ 2 kutoka 0 hadi 2. Ni kuanzisha kwa ajili ya haki endpoint makadirio juu ya eneo [1,2], ambayo ni kinachoitwa a=x0 kwa x4. Ni jumla ya juu.$

Mfano$\PageIndex{6}$: Finding Lower and Upper Sums for $f(x)=\sin x$

Pata kiasi cha chini kwa$f(x)=\sin x$ zaidi ya muda$[a,b]=\left[0,\frac{π}{2} \right]$; basi$n=6.$

Suluhisho

Hebu tuangalie kwanza grafu katika Kielelezo$\PageIndex{14}$ ili kupata wazo bora la eneo la riba.

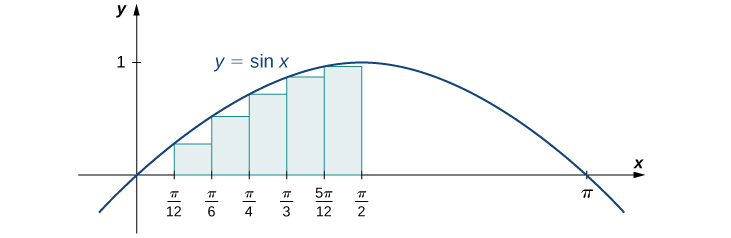
Grafu ya kazi y = dhambi (x) kutoka 0 hadi pi. Ni kuanzisha kwa upande wa kushoto endpoint makadirio kutoka 0 kwa pi/2 na n = 6. Ni jumla ya chini. — Kielelezo$\PageIndex{14}$: Grafu ya$y=\sin x$ imegawanywa katika mikoa sita:$Δx=\dfrac{π/2}{6}=\dfrac{π}{12}$.

vipindi ni$\left[0,\frac{π}{12}\right],\,\left[\frac{π}{12},\frac{π}{6}\right],\,\left[\frac{π}{6},\frac{π}{4}\right],\,\left[\frac{π}{4},\frac{π}{3}\right],\,\left[\frac{π}{3},\frac{5π}{12}\right]$, na$\left[\frac{5π}{12},\frac{π}{2}\right]$. Kumbuka kuwa$f(x)=\sin x$ ni kuongeza juu ya muda$\left[0,\frac{π}{2}\right]$, hivyo kushoto-mwisho makadirio inatupa jumla ya chini. kushoto-mwisho makadirio ni Riemann jumla$\sum_{i=0}^5\sin x_i\left(\tfrac{π}{12}\right)$ .Tuna

\[A≈\sin(0)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{12}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{6}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{4}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{π}{3}\right)\left(\tfrac{π}{12}\right)+\sin\left(\tfrac{5π}{12}\right)\left(\tfrac{π}{12}\right)\approx 0.863 \,\text{units}^2. \nonumber \]

Zoezi$\PageIndex{6}$

Kutumia kazi$f(x)=\sin x$ juu ya muda$\left[0,\frac{π}{2}\right],$ kupata jumla ya juu; basi$n=6.$

Kidokezo: Fuata hatua kutoka Mfano$\PageIndex{6}$.

Jibu: $A≈1.125 \,\text{units}^2$

Dhana muhimu

Matumizi ya sigma (summation) notation ya fomu$\displaystyle \sum_{i=1}^na_i$ ni muhimu kwa kuonyesha kiasi cha maadili ya muda mrefu katika fomu ya compact.
Kwa kazi ya kuendelea inavyoelezwa juu$[a,b],$ ya muda mchakato wa kugawanya muda katika sehemu$n$ sawa, kupanua mstatili kwenye grafu ya kazi, kuhesabu maeneo ya mfululizo wa rectangles, na kisha kuhesabu maeneo ya mavuno makadirio ya eneo hilo.
Wakati wa kutumia ugawaji wa kawaida, upana wa kila mstatili ni$Δx=\dfrac{b−a}{n}$.
Riemann kiasi ni maneno ya fomu$\displaystyle \sum_{i=1}^nf(x^∗_i)Δx,$ na inaweza kutumika kukadiria eneo chini ya Curve$y=f(x).$ kushoto- na makadirio haki-mwisho ni aina maalum ya Riemann kiasi ambapo maadili ya${x^∗_i}$ huchaguliwa kuwa kushoto au kulia endpoints ya subspinternations, mtiririko.
Riemann kiasi kuruhusu kubadilika sana katika kuchagua seti ya pointi${x^∗_i}$ ambayo kazi ni tathmini, mara nyingi kwa jicho kupata kiasi cha chini au jumla ya juu.

Mlinganyo muhimu

Mali ya Sigma Notation

\ [kuanza {align*}\ sum_ {i = 1} ^nc&=nc\\ [4pt]
\ sum_ {i = 1} ^nca_i &=c\ sum_ {i =1} ^na_i\\ [4pt]
\ sum_ {i = 1} ^n (a_i+b_i) &=\ sum_ {i = 1} ^na_na_i i+\ sum_ {i = 1} ^nb_i\\ [4pt]
\ sum_ {i = 1} ^n (a_i-b_i) &=\ sum_ {i =1} ^na_i-\ sum_ {i = 1} ^nb_i\\ [4pt]
\ sum_ {i = 1} ^na_i & =\ sum_ {i=1} ^ma_i+\ sum_ {i = m+1} ^na_i\ mwisho {align*}\]

Sums na Mamlaka ya Integers

\[\sum_{i=1}^ni=1+2+⋯+n=\dfrac{n(n+1)}{2} \nonumber \]

\[\sum_{i=1}^ni^2=1^2+2^2+⋯+n^2=\dfrac{n(n+1)(2n+1)}{6} \nonumber \]

\[\sum_{i=0}^ni^3=1^3+2^3+⋯+n^3=\dfrac{n^2(n+1)^2}{4} \nonumber \]

Kushoto-mwisho makadirio

$A≈L_n=f(x_0)Δx+f(x_1)Δx+⋯+f(x_{n−1})Δx=\displaystyle \sum_{i=1}^nf(x_{i−1})Δx$

Ukadiriaji wa mwisho wa haki-mwisho

$A≈R_n=f(x_1)Δx+f(x_2)Δx+⋯+f(x_n)Δx=\displaystyle \sum_{i=1}^nf(x_i)Δx$

faharasa

makadirio ya kushoto-mwisho: makadirio ya eneo chini ya Curve iliyohesabiwa kwa kutumia mwisho wa kushoto wa kila subinterval ili kuhesabu urefu wa pande za wima za kila mstatili

jumla ya chini: jumla kupatikana kwa kutumia thamani ya chini ya$f(x)$ juu ya kila subinterval

kugawanya: seti ya pointi ambazo hugawanya muda katika vipindi

ugawaji wa kawaida: kizigeu ambacho sehemu ndogo zote zina upana sawa

riemann jumla: makadirio ya eneo chini ya pembe ya fomu$A≈\displaystyle \sum_{i=1}^nf(x^∗_i)Δx$

makadirio ya mwisho wa haki-mwisho: makadirio ya mwisho wa haki-mwisho ni makadirio ya eneo la mstatili chini ya pembe kwa kutumia mwisho wa kila subinterval ili kujenga pande za wima za kila mstatili

sigma nukuu: (pia, maelezo ya muhtasari) barua ya Kigiriki sigma ($Σ$) inaonyesha kuongeza maadili; maadili ya index hapo juu na chini ya sigma yanaonyesha wapi kuanza summation na wapi kumaliza

jumla ya juu: Jumla kupatikana kwa kutumia thamani ya$f(x)$ juu ya kila subinterval

Thamani ya\(n\)	Eneo la Takriban\(L_n\)	Eneo la Takriban\(R_n\)
\ (n\)” style="wima align:katikati; ">\(n=4\)	\ (L_n\)” style="wima align:katikati; ">\(7.5\)	\ (R_n\)” style="wima align:katikati; ">\(8.5\)
\ (n\)” style="wima align:katikati; ">\(n=8\)	\ (L_n\)” style="wima align:katikati; ">\(7.75\)	\ (R_n\)” style="wima align:katikati; ">\(8.25\)
\ (n\)” style="wima align:katikati; ">\(n=32\)	\ (L_n\)” style="wima align:katikati; ">\(7.94\)	\ (R_n\)” style="wima align:katikati; ">\(8.06\)

Mfano\(\PageIndex{1}\): Using Sigma Notation

Zoezi\(\PageIndex{1}\)

Kanuni: Mali ya Sigma Notation

Ushahidi

Kanuni: Sums na Mamlaka ya Integers

Mfano\(\PageIndex{2}\): Evaluation Using Sigma Notation

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{3}\): Finding the Sum of the Function Values

Zoezi\(\PageIndex{3}\)

Ufafanuzi: Sehemu

Kanuni: Upimaji wa mwisho wa kushoto

Kanuni: Upimaji wa Mwisho wa Haki

Mfano\(\PageIndex{4}\): Approximating the Area Under a Curve

Zoezi\(\PageIndex{4}\)

ufafanuzi: Riemann jumla

Ufafanuzi: Eneo Chini ya Curve

Mfano\(\PageIndex{5}\): Finding Lower and Upper Sums

Zoezi\(\PageIndex{5}\)

Mfano\(\PageIndex{6}\): Finding Lower and Upper Sums for \(f(x)=\sin x\)

Zoezi\(\PageIndex{6}\)