4.7: Matatizo ya Uboreshaji wa Matumizi

Last updated
Save as PDF

Page ID: 178842

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Weka na kutatua matatizo ya uboreshaji katika maeneo kadhaa yaliyotumika.

Matumizi moja ya kawaida ya calculus ni kuhesabu thamani ya chini au ya juu ya kazi. Kwa mfano, makampuni mara nyingi wanataka kupunguza gharama za uzalishaji au kuongeza mapato. Katika viwanda, mara nyingi ni muhimu kupunguza kiasi cha nyenzo zilizotumiwa kutengeneza bidhaa kwa kiasi fulani. Katika sehemu hii, tunaonyesha jinsi ya kuanzisha aina hizi za matatizo ya kupunguza na maximization na kutatua kwa kutumia zana zilizotengenezwa katika sura hii.

Kutatua Matatizo ya Uboreshaji juu ya Muda uliofungwa, uliowekwa

Wazo la msingi la matatizo ya uboreshaji yanayofuata ni sawa. Tuna kiasi fulani ambacho tuna nia ya kuongeza au kupunguza. Hata hivyo, tuna pia hali ya msaidizi ambayo inahitaji kuridhika. Kwa mfano, katika Mfano$\PageIndex{1}$, tuna nia ya kuongeza eneo la bustani ya mstatili. Hakika, ikiwa tunaendelea kufanya urefu wa bustani kubwa, eneo hilo litaendelea kuwa kubwa. Hata hivyo, ni nini ikiwa tuna kizuizi juu ya kiasi gani cha uzio tunaweza kutumia kwa mzunguko? Katika hali hii, hatuwezi kufanya bustani iwe kubwa kama tunavyopenda. Hebu tuangalie jinsi tunaweza kuongeza eneo la mstatili chini ya kikwazo fulani kwenye mzunguko.

Mfano$\PageIndex{1}$: Maximizing the Area of a Garden

Bustani ya mstatili inapaswa kujengwa kwa kutumia ukuta wa mwamba kama upande mmoja wa bustani na uzio wa waya kwa pande nyingine tatu (Kielelezo$\PageIndex{1}$). Kutokana$100\,\text{ft}$ na uzio wa waya, tambua vipimo ambavyo vinaweza kujenga bustani ya eneo la juu. Eneo la juu ni nini?

Mchoro wa bustani una x na y iliyoandikwa kwenye pande za wima na za usawa, kwa mtiririko huo. Kuna ukuta wa mwamba unaoendesha pamoja na urefu wote wa chini wa usawa wa kuchora. — Kielelezo$\PageIndex{1}$: Tunataka kuamua vipimo$x$ na$y$ ambayo itaunda bustani yenye eneo la juu kwa kutumia$100\,\text{ft}$ uzio.

Suluhisho

Hebu$x$ kuashiria urefu wa upande wa bustani perpendicular kwa ukuta wa mwamba na$y$ kuashiria urefu wa upande sambamba na ukuta wa mwamba. Kisha eneo la bustani ni

$A=x⋅y.$

Tunataka kupata eneo la juu linalowezekana chini ya kikwazo ambacho uzio wa jumla ni$100\,\text{ft}$. Kutoka Kielelezo$\PageIndex{1}$, jumla ya uzio kutumika itakuwa$2x+y.$ Kwa hiyo, equation kikwazo ni

$2x+y=100.$

Kutatua equation hii kwa$y$, tuna$y=100−2x.$ Hivyo, tunaweza kuandika eneo kama

$A(x)=x⋅(100−2x)=100x−2x^2.$

Kabla ya kujaribu kuongeza kazi ya eneo$A(x)=100x−2x^2,$ tunahitaji kuamua uwanja unaozingatiwa. Ili kujenga bustani ya mstatili, hakika tunahitaji urefu wa pande zote mbili kuwa chanya. Kwa hiyo, tunahitaji$x>0$ na$y>0$. Tangu$y=100−2x$, ikiwa$y>0$, basi$x<50$. Kwa hiyo, tunajaribu kuamua thamani ya$A(x)$$x$ juu ya muda wa wazi$(0,50)$. Hatujui kwamba kazi lazima ina thamani ya juu juu ya muda wa wazi. Hata hivyo, tunajua kwamba kazi inayoendelea ina kiwango cha juu kabisa (na kiwango cha chini kabisa) juu ya muda uliofungwa. Kwa hiyo, hebu fikiria kazi$A(x)=100x−2x^2$ juu ya muda uliofungwa$[0,50]$. Ikiwa thamani ya juu hutokea kwenye hatua ya mambo ya ndani, basi tumepata thamani$x$ katika kipindi cha wazi$(0,50)$ ambacho kinaongeza eneo la bustani.

Kwa hiyo, tunazingatia tatizo linalofuata:

Kuongeza$A(x)=100x−2x^2$ zaidi ya muda$[0,50].$

Kama ilivyoelezwa hapo awali, tangu$A$ ni kazi inayoendelea kwenye muda uliofungwa, umefungwa, na theorem ya thamani kali, ina kiwango cha juu na cha chini. Maadili haya makubwa hutokea ama mwisho au pointi muhimu. Katika mwisho,$A(x)=0$. Kwa kuwa eneo hilo ni chanya kwa wote$x$ katika kipindi cha wazi$(0,50)$, kiwango cha juu kinapaswa kutokea kwa hatua muhimu. Kutofautisha kazi$A(x)$, tunapata

$A′(x)=100−4x.$

Kwa hiyo, hatua pekee muhimu ni$x=25$ (Kielelezo$\PageIndex{2}$). Tunahitimisha kuwa eneo la juu linapaswa kutokea wakati$x=25$.

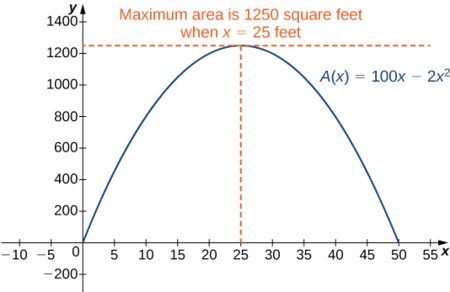
Kazi A (x) = 100x - 2x ni graphed. Katika upeo wake kuna makutano ya mistari miwili iliyopigwa na maandishi ambayo inasoma “Eneo la juu ni futi za mraba 1250 wakati x = futi 25.” — Kielelezo$\PageIndex{2}$: Ili kuongeza eneo la bustani, tunahitaji kupata thamani ya juu ya kazi$A(x)=100x−2x^2$.

Kisha tuna$y=100−2x=100−2(25)=50.$ Ili kuongeza eneo la bustani, basi$x=25\,\text{ft}$ na$y=50\,\text{ft}$. Eneo la bustani hii ni$1250\, \text{ft}^2$.

Zoezi$\PageIndex{1}$

Kuamua eneo la juu kama tunataka kufanya bustani sawa mstatili kama katika Kielelezo$\PageIndex{2}$, lakini tuna$200\,\text{ft}$ uzio.

Kidokezo: Tunahitaji kuongeza kazi$A(x)=200x−2x^2$ zaidi ya muda$[0,100].$

Jibu: Eneo la juu ni$5000\, \text{ft}^2$.

Sasa hebu tuangalie mkakati wa jumla wa kutatua matatizo ya ufanisi sawa na Mfano$\PageIndex{1}$.

Mkakati wa Kutatua Matatizo: Kutatua Matatizo ya Biashara

Tangaza vigezo vyote. Ikiwa inatumika, futa takwimu na uandike vigezo vyote.
Kuamua ni kiasi gani kinachopunguzwa au kupunguzwa, na kwa maadili gani ya vigezo vingine (kama hii inaweza kuamua kwa wakati huu).
Andika formula kwa wingi kuwa maximized au kupunguzwa katika suala la vigezo. Fomula hii inaweza kuhusisha variable zaidi ya moja.
Andika milinganyo yoyote inayohusiana na vigezo vya kujitegemea katika fomu kutoka hatua$3$. Tumia equations hizi kuandika wingi kuwa maximized au kupunguzwa kama kazi ya variable moja.
Tambua uwanja wa kuzingatia kwa kazi kwa hatua$4$ kulingana na tatizo la kimwili kutatuliwa.
Pata thamani ya juu au ya chini ya kazi kutoka hatua Hatua$4.$ hii inahusisha kutafuta pointi muhimu na kutathmini kazi kwenye mwisho.

Sasa hebu tufanye mkakati huu ili kuongeza kiasi cha sanduku la wazi lililopewa kikwazo juu ya kiasi cha nyenzo zitakazotumiwa.

Mfano$\PageIndex{2}$: Maximizing the Volume of a Box

Sanduku la wazi linapaswa kufanywa kutoka$24\,\text{in.}$ kwa$36\,\text{in.}$ kipande cha kadibodi kwa kuondoa mraba kutoka kila kona ya sanduku na kukunja flaps kila upande. Ni ukubwa gani mraba unapaswa kukatwa nje ya kila kona ili kupata sanduku na kiasi cha juu?

Suluhisho

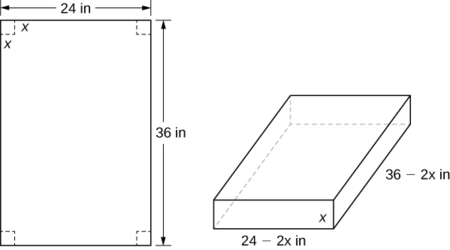
Hatua ya 1: Hebu$x$ uwe urefu wa mraba ili uondolewe kutoka kila kona (Kielelezo$\PageIndex{3}$). Kisha, flaps nne zilizobaki zinaweza kupandwa ili kuunda sanduku la wazi. Hebu$V$ iwe kiasi cha sanduku linalosababisha.

Kuna takwimu mbili za takwimu hii. Ya kwanza ni mstatili na pande 24 ndani na 36 ndani, na kila kona kuwa na mraba wa urefu wa upande x kuchukuliwa nje yake. Katika picha ya pili, kuna sanduku na urefu wa upande x katika, 24 - 2x katika, na 36 - 2x katika. — Kielelezo$\PageIndex{3}$: Mraba yenye$x$ inchi za urefu wa upande huondolewa kutoka kila kona ya kipande cha kadi. Vipande vilivyobaki vimewekwa ili kuunda sanduku la wazi.

Hatua ya 2: Tunajaribu kuongeza kiasi cha sanduku. Kwa hiyo, tatizo ni kuongeza$V$.

Hatua ya 3: Kama ilivyoelezwa katika hatua ya 2, wanajaribu kuongeza kiasi cha sanduku. Kiasi cha sanduku ni

\[V=L⋅W⋅H \nonumber, \nonumber \]

wapi$L,\,W,$ na$H$ urefu, upana, na urefu, kwa mtiririko huo.

Hatua ya 4: Kutoka Kielelezo$\PageIndex{3}$, tunaona kwamba urefu wa sanduku ni$x$ inchi, urefu ni$36−2x$ inchi, na upana ni$24−2x$ inchi. Kwa hiyo, kiasi cha sanduku ni

\[ \begin{align*} V(x) &=(36−2x)(24−2x)x \\[4pt] &=4x^3−120x^2+864x \end{align*}. \nonumber \]

Hatua ya 5: Kuamua uwanja wa kuzingatia, hebu tuchunguze Kielelezo$\PageIndex{3}$. Hakika, tunahitaji$x>0.$ Aidha, upande urefu wa mraba hawezi kuwa kubwa kuliko au sawa na nusu urefu wa upande mfupi,$24\,\text{in.}$; vinginevyo, moja ya flaps itakuwa kabisa kukatwa. Kwa hiyo, tunajaribu kuamua kama kuna kiasi cha juu cha sanduku kwa$x$ zaidi ya muda wa wazi$(0,12).$ Tangu$V$ ni kazi inayoendelea juu ya muda uliofungwa$[0,12]$, tunajua$V$ itakuwa na kiwango cha juu kabisa juu ya muda uliofungwa. Kwa hiyo, tunazingatia$V$ juu ya muda uliofungwa$[0,12]$ na uangalie kama kiwango cha juu kabisa kinatokea katika hatua ya mambo ya ndani.

Hatua ya 6: Kwa kuwa$V(x)$ ni kazi ya kuendelea juu ya kufungwa, imepakana muda$[0,12]$,$V$ lazima uwe na kiwango cha juu kabisa (na kiwango cha chini kabisa). Tangu$V(x)=0$ mwisho na$V(x)>0$ kwa kiwango$0<x<12,$ cha juu lazima kutokea kwa hatua muhimu. Derivative ni

$V′(x)=12x^2−240x+864.$

Ili kupata pointi muhimu, tunahitaji kutatua equation

$12x^2−240x+864=0.$

Kugawanya pande zote mbili za equation hii na$12$, tatizo simplifies kutatua equation

$x^2−20x+72=0.$

Kutumia formula ya quadratic, tunaona kwamba pointi muhimu ni

\[\begin{align*} x &=\dfrac{20±\sqrt{(−20)^2−4(1)(72)}}{2} \\[4pt] &=\dfrac{20±\sqrt{112}}{2} \\[4pt] &=\dfrac{20±4\sqrt{7}}{2} \\[4pt] &=10±2\sqrt{7} \end{align*}. \nonumber \]

Kwa kuwa$10+2\sqrt{7}$ sio katika uwanja wa kuzingatia, hatua muhimu tu tunayohitaji kuzingatia ni$10−2\sqrt{7}$. Kwa hiyo, kiasi ni maximized kama sisi basi$x=10−2\sqrt{7}\,\text{in.}$ Kiwango cha juu ni

\[V(10−2\sqrt{7})=640+448\sqrt{7}≈1825\,\text{in}^3. \nonumber \]

kama inavyoonekana katika grafu ifuatayo.

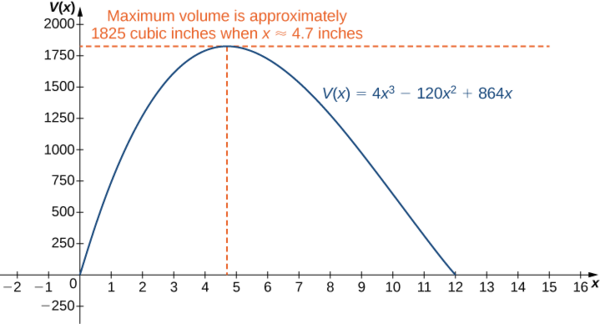
Kazi V (x) = 4x3 - 120x2 + 864x imewekwa. Katika upeo wake kuna makutano ya mistari miwili iliyopigwa na maandishi ambayo inasoma “Kiwango cha juu cha kiasi ni takriban inchi za ujazo 1825 wakati x ≈ inchi 4.7.” — Kielelezo$\PageIndex{4}$: Kuongeza kiasi cha sanduku kunasababisha kupata thamani ya juu ya polynomial ya ujazo.

Zoezi$\PageIndex{2}$

Tuseme vipimo vya kadi katika Mfano$\PageIndex{2}$ ni$20\,\text{in.}$ kwa$30\,\text{in.}$ Hebu$x$ uwe urefu wa kila mraba na uandike kiasi cha sanduku la wazi la juu kama kazi ya$x$. Kuamua uwanja wa kuzingatia kwa$x$.

Kidokezo: Kiasi cha sanduku ni$L⋅W⋅H.$

Jibu: $V(x)=x(20−2x)(30−2x).$Kikoa ni$[0,10]$.

Mfano$\PageIndex{3}$: Minimizing Travel Time

Kisiwa ni$2$ mi kutokana kaskazini ya hatua yake ya karibu pamoja pwani moja kwa moja. mgeni ni kukaa katika cabin pwani yaani$6$ mi magharibi ya hatua hiyo. Mgeni anapanga kwenda kutoka cabin hadi kisiwa hicho. Tuseme mgeni anaendesha kwa kiwango cha$8$ mph na kuogelea kwa kiwango cha$3$ mph. Je, mgeni anapaswa kukimbia kabla ya kuogelea ili kupunguza muda unachukua kufikia kisiwa hicho?

Suluhisho

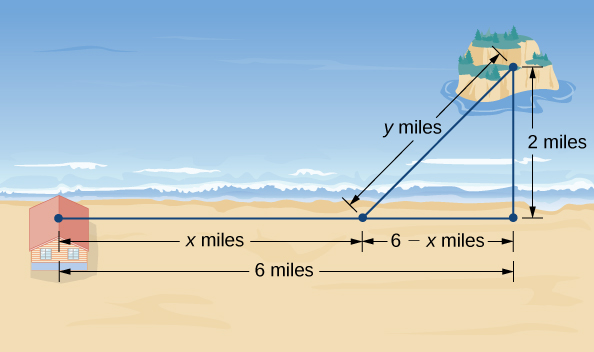
Hatua ya 1: Hebu$x$ uwe umbali unaoendesha na$y$ uwe umbali wa kuogelea (Kielelezo$\PageIndex{5}$). Hebu$T$ iwe wakati inachukua kupata kutoka cabin hadi kisiwa hicho.

cabin ni x maili kutoka pwani. Kutoka hatua hiyo pwani, kisiwa ni y maili mbali. Kama ungekuwa na kuendelea line kutoka cabin kwa pwani (x maili moja) na kama ungekuwa na kuteka mstari kutoka kisiwa sambamba na pwani, mistari itakuwa kupanua 2 maili kutoka kisiwa na 6 maili kutoka cabin kabla intersecting. — Kielelezo$\PageIndex{5}$:$x$ Tunawezaje$y$ kuchagua na kupunguza muda wa kusafiri kutoka cabin hadi kisiwa hicho?

Hatua ya 2: Tatizo ni kupunguza$T$.

Hatua ya 3: Ili kupata muda uliotumika kusafiri kutoka cabin hadi kisiwa hicho, ongeza muda uliotumiwa na wakati uliotumika kuogelea. Tangu Umbali = Kiwango ×$(D=R×T),$ Muda uliotumika kukimbia ni

$T_{running}=\dfrac{D_{running}}{R_{running}}=\dfrac{x}{8}$,

na wakati uliotumika kuogelea ni

$T_{swimming}=\dfrac{D_{swimming}}{R_{swimming}}=\dfrac{y}{3}$.

Kwa hiyo, jumla ya muda alitumia kusafiri ni

$T=\dfrac{x}{8}+\dfrac{y}{3}$.

Hatua ya 4: Kutoka Kielelezo$\PageIndex{5}$, sehemu ya mstari wa$y$ maili huunda hypotenuse ya pembetatu sahihi na miguu ya urefu$2$ mi na$6−x$ mi. Kwa hiyo, kwa theorem ya Pythagorean$2^2+(6−x)^2=y^2$, na tunapata$y=\sqrt{(6−x)^2+4}$. Hivyo, jumla ya muda uliotumika kusafiri hutolewa na kazi

$T(x)=\dfrac{x}{8}+\dfrac{\sqrt{(6−x)^2+4}}{3}$.

Hatua ya 5: Kutoka Kielelezo$\PageIndex{5}$, tunaona hiyo$0≤x≤6$. Kwa hiyo,$[0,6]$ ni uwanja wa kuzingatia.

Hatua 6: Kwa kuwa$T(x)$ ni kazi ya kuendelea juu ya kufungwa, imepakana muda, ina kiwango cha juu na kiwango cha chini. Hebu tuanze kwa kuangalia pointi yoyote muhimu ya$T$ zaidi ya muda. derivative ni$[0,6].$

\[\begin{align*} T′(x) &=\dfrac{1}{8}−\dfrac{1}{2}\dfrac{[(6−x)^2+4]^{−1/2}}{3}⋅2(6−x) \\[4pt] &=\dfrac{1}{8}−\dfrac{(6−x)}{3\sqrt{(6−x)^2+4}} \end{align*}\]

Ikiwa$T′(x)=0,$, basi

\[\dfrac{1}{8}=\dfrac{6−x}{3\sqrt{(6−x)^2+4}} \label{ex3eq1} \]

Kwa hiyo,

\[3\sqrt{(6−x)^2+4}=8(6−x). \label{ex3eq2} \]

Squaring pande zote mbili za equation hii, tunaona kwamba kama$x$ satisfies equation hii, basi$x$ lazima kukidhi

\[9[(6−x)^2+4]=64(6−x)^2,\nonumber \]

ambayo ina maana

\[55(6−x)^2=36. \nonumber \]

Tunahitimisha kwamba kama$x$ ni hatua muhimu, basi$x$ satisfies

\[(x−6)^2=\dfrac{36}{55}. \nonumber \]

[Kumbuka kwamba tangu sisi ni squaring,$ (x-6)^2 = (6-x)^2.$]

Kwa hiyo, uwezekano wa pointi muhimu ni

\[x=6±\dfrac{6}{\sqrt{55}}.\nonumber \]

Kwa kuwa$x=6+6/\sqrt{55}$ si katika uwanja, si uwezekano kwa hatua muhimu. Kwa upande mwingine,$x=6−6/\sqrt{55}$ ni katika uwanja. Tangu sisi squared pande zote mbili za Equation\ ref {ex3eq2} ili kufika pointi muhimu iwezekanavyo, inabakia kuthibitisha kwamba$x=6−6/\sqrt{55}$ satisfies Equation\ ref {ex3eq1}. Kwa kuwa$x=6−6/\sqrt{55}$ haina kukidhi kwamba equation, sisi kuhitimisha kwamba$x=6−6/\sqrt{55}$ ni hatua muhimu, na ni moja tu. Ili kuhalalisha kwamba wakati unapunguzwa kwa thamani hii ya$x$, tunahitaji tu kuangalia maadili ya$T(x)$ mwisho$x=0$ na$x=6$, na kulinganisha nao na thamani ya$T(x)$ katika hatua muhimu$x=6−6/\sqrt{55}$. Tunaona kwamba$T(0)≈2.108\,\text{h}$ na$T(6)≈1.417\,\text{h}$, wakati

\[T(6−6/\sqrt{55})≈1.368\,\text{h}. \nonumber \]

Kwa hiyo, tunahitimisha kuwa$T$ ina kiwango cha chini cha ndani katika$x≈5.19$ mi.

Zoezi$\PageIndex{3}$

Tuseme kisiwa hicho ni$1$ mi kutoka pwani, na umbali kutoka cabin hadi kwenye pwani karibu na kisiwa ni$15$ mi. Tuseme mgeni kuogelea kwa kiwango cha$2.5$ mph na anaendesha kwa kiwango cha$6$ mph. Hebu$x$ kuashiria umbali mgeni kukimbia kabla ya kuogelea, na kupata kazi kwa muda inachukua mgeni kupata kutoka cabin kisiwa.

Kidokezo: wakati$T=T_{running}+T_{swimming}.$

Jibu: $T(x)=\dfrac{x}{6}+\dfrac{\sqrt{(15−x)^2+1}}{2.5} $

Katika biashara, makampuni ni nia ya kuongeza mapato. Katika mfano unaofuata, tunazingatia hali ambayo kampuni imekusanya data juu ya magari ngapi ambayo ina uwezo wa kukodisha, kulingana na bei ambayo inawadai wateja wake kukodisha gari. Hebu tutumie data hizi ili kuamua bei ambayo kampuni inapaswa kulipa ili kuongeza kiasi cha fedha kinacholeta.

Mfano$\PageIndex{4}$: Maximizing Revenue

Wamiliki wa kampuni ya kukodisha gari wameamua kwamba ikiwa$p$ wanatoa dola za wateja kwa siku kukodisha gari$50≤p≤200$, ambapo, idadi ya magari$n$ wanayokodisha kwa siku inaweza kuonyeshwa na kazi ya mstari$n(p)=1000−5p$. Kama malipo$$50$ kwa siku au chini, wao kodi ya magari yao yote. Kama malipo$$200$ kwa siku au zaidi, wao si kukodisha magari yoyote. Kwa kuzingatia wamiliki wanapanga kulipa wateja kati ya$$50$ siku na$$200$ kwa siku kukodisha gari, ni kiasi gani wanapaswa kulipia ili kuongeza mapato yao?

Suluhisho

Hatua ya 1: Hebu$p$ kuwa bei kushtakiwa kwa gari kwa siku na hebu$n$ kuwa idadi ya magari kukodi kwa siku. Hebu$R$ kuwa mapato kwa siku.

Hatua ya 2: Tatizo ni kuongeza$R.$

Hatua ya 3: Mapato (kwa siku) ni sawa na idadi ya magari yaliyokodishwa kwa siku mara bei inayotozwa kwa gari kwa siku—yaani,$R=n×p.$

Hatua ya 4: Kwa kuwa idadi ya magari yaliyokodishwa kwa siku inatokana na kazi$n(p)=1000−5p,$ ya mstari, mapato$R$ yanaweza kuwakilishwa na kazi

\[ \begin{align*} R(p) &=n×p \\[4pt] &=(1000−5p)p \\[4pt] &=−5p^2+1000p.\end{align*}\]

Hatua ya 5: Kwa kuwa wamiliki wanapanga kulipa kati$$50$ ya gari kwa$$200$ siku na kwa gari kwa siku, tatizo ni kupata mapato ya juu$R(p)$$p$ kwa muda uliofungwa$[50,200]$.

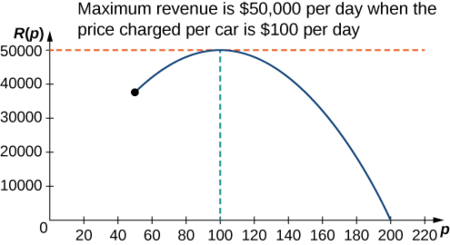
Hatua ya 6: Kwa kuwa$R$ ni kazi ya kuendelea juu ya kufungwa, imepakana muda$[50,200]$, ina kiwango cha juu kabisa (na kiwango cha chini kabisa) katika kipindi hicho. Ili kupata thamani ya juu, angalia pointi muhimu. derivative ni$R′(p)=−10p+1000.$ Kwa hiyo, hatua muhimu ni$p=100$. Wakati$p=100, R(100)=$50,000.$ Wakati$p=50, R(p)=$37,500$. Wakati$p=200, R(p)=$0$.

Kwa hiyo, kiwango cha juu kabisa hutokea$p=$100$. Kampuni ya kukodisha gari inapaswa$$100$ kulipia kwa siku kwa gari ili kuongeza mapato kama inavyoonekana katika takwimu ifuatayo.

Kazi R (p) imefunikwa. Katika upeo wake kuna makutano ya mistari miwili iliyopigwa na maandishi ambayo inasoma “Mapato ya kiwango cha juu ni $50,000 kwa siku wakati bei ya kushtakiwa kwa gari ni dola 100 kwa siku.” — Kielelezo$\PageIndex{6}$: Ili kuongeza mapato, kampuni ya kukodisha gari inapaswa kusawazisha bei ya kukodisha dhidi ya idadi ya magari ambayo watu watakodisha kwa bei hiyo.

Zoezi$\PageIndex{4}$

Kampuni ya kukodisha gari inadai wateja wake$p$ dola kwa siku, ambapo$60≤p≤150$. Imegundua kwamba idadi ya magari ya kukodishwa kwa siku inaweza kuwa inatokana na kazi linear kiasi$n(p)=750−5p.$ gani kampuni lazima malipo ya kila mteja ili kuongeza mapato?

Kidokezo: $R(p)=n×p,$ambapo$n$ ni idadi ya magari ya kukodi na$p$ ni bei kushtakiwa kwa gari.

Jibu: Kampuni hiyo inapaswa malipo$$75$ kwa gari kwa siku.

Mfano$\PageIndex{5}$: Maximizing the Area of an Inscribed Rectangle

Mstatili ni kuandikwa katika duaradufu

\[\dfrac{x^2}{4}+y^2=1. \nonumber \]

Je! Vipimo vya mstatili vinapaswa kuongeza eneo lake? Eneo la juu ni nini?

Suluhisho

Hatua ya 1: Kwa mstatili kuandikwa kwenye duaradufu, pande za mstatili lazima iwe sawa na axes. Hebu$L$ iwe urefu wa mstatili na$W$ uwe upana wake. Hebu$A$ iwe eneo la mstatili.

duaradufu x2/4 + y2 = 1 ni inayotolewa na x yake intercepts kuwa ± 2 na y yake intercepts kuwa ± 1. Kuna mstatili ulioandikwa katika duaradufu na urefu L (katika mwelekeo wa x) na upana W. — Kielelezo$\PageIndex{7}$: Tunataka kuongeza eneo la mstatili ulioandikwa katika ellipse.

Hatua ya 2: Tatizo ni kuongeza$A$.

Hatua ya 3: Eneo la mstatili ni$A=LW.$

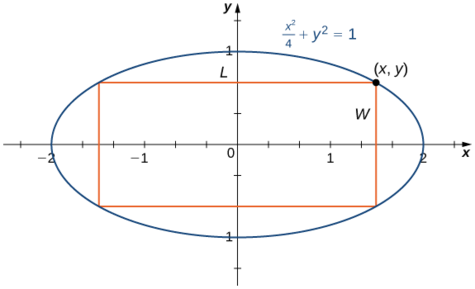
Hatua ya 4: Hebu$(x,y)$ iwe kona ya mstatili ulio katika quadrant ya kwanza, kama inavyoonekana kwenye Mchoro$\PageIndex{7}$. Tunaweza kuandika urefu$L=2x$ na upana$W=2y$. Tangu$\dfrac{x^2}{4}+y^2=1$ na$y>0$, tuna$y=\sqrt{1-\dfrac{x^2}{4}}$. Kwa hiyo, eneo hilo ni

$A=LW=(2x)(2y)=4x\sqrt{1-\dfrac{x^2}{4}}=2x\sqrt{4−x^2}$

Hatua ya 5: Kutoka Kielelezo$\PageIndex{7}$, tunaona kwamba kuandika mstatili katika duaradufu,$x$ -kuratibu ya kona katika quadrant ya kwanza inapaswa kukidhi$0<x<2$. Kwa hiyo, tatizo hupunguza kutafuta thamani ya$A(x)$ juu ya muda wa wazi$(0,2)$. Kwa kuwa$A(x)$ itakuwa na kiwango cha juu kabisa (na kiwango cha chini kabisa) juu ya muda uliofungwa$[0,2]$, tunazingatia$A(x)=2x\sqrt{4−x^2}$ zaidi ya muda$[0,2]$. Ikiwa upeo kabisa hutokea katika hatua ya mambo ya ndani, basi tumepata kiwango cha juu kabisa katika kipindi cha wazi.

Hatua 6: Kama ilivyoelezwa hapo awali,$A(x)$ ni kazi ya kuendelea juu ya kufungwa, imepakana muda$[0,2]$. Kwa hiyo, ina kiwango cha juu kabisa (na kiwango cha chini kabisa). Katika endpoints$x=0$ na$x=2$,$A(x)=0.$ kwa$0<x<2$,$A(x)>0$.

Kwa hiyo, kiwango cha juu kinapaswa kutokea kwa hatua muhimu. Kuchukua derivative ya$A(x)$, sisi kupata

\[ \begin{align*} A'(x) &=2\sqrt{4−x^2}+2x⋅\dfrac{1}{2\sqrt{4−x^2}}(−2x) \\[4pt] &=2\sqrt{4−x^2}−\dfrac{2x^2}{\sqrt{4−x^2}} \\[4pt] &=\dfrac{8−4x^2}{\sqrt{4−x^2}} . \end{align*}\]

Ili kupata pointi muhimu, tunahitaji kupata ambapo$A'(x)=0.$ Tunaweza kuona kwamba ikiwa$x$ ni suluhisho la

\[\dfrac{8−4x^2}{\sqrt{4−x^2}}=0, \label{ex5eq1} \]

basi$x$ lazima kukidhi

\[8−4x^2=0. \nonumber \]

Kwa hiyo,$x^2=2.$ hivyo,$x=±\sqrt{2}$ ni ufumbuzi iwezekanavyo wa Equation\ ref {ex5eq1}. Kwa kuwa sisi ni kuzingatia$x$ zaidi ya muda$[0,2]$,$x=\sqrt{2}$ ni uwezekano kwa hatua muhimu, lakini$x=−\sqrt{2}$ si. Kwa hiyo, sisi kuangalia kama$\sqrt{2}$ ni ufumbuzi wa Equation\ ref {ex5eq1}. Tangu$x=\sqrt{2}$ ni suluhisho la Equation\ ref {ex5eq1}, tunahitimisha kuwa$\sqrt{2}$ ni hatua muhimu tu ya$A(x)$ katika kipindi$[0,2]$.

Kwa hiyo,$A(x)$ lazima uwe na kiwango cha juu kabisa katika hatua muhimu$x=\sqrt{2}$. Kuamua vipimo vya mstatili, tunahitaji kupata urefu$L$ na upana$W$. Kama$x=\sqrt{2}$ basi

\[y=\sqrt{1−\dfrac{(\sqrt{2})^2}{4}}=\sqrt{1−\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}.\nonumber \]

Kwa hiyo, vipimo vya mstatili ni$L=2x=2\sqrt{2}$ na$W=2y=\dfrac{2}{\sqrt{2}}=\sqrt{2}$. Eneo la mstatili huu ni$ A=LW=(2\sqrt{2})(\sqrt{2})=4.$

Zoezi$\PageIndex{5}$

Badilisha kazi ya eneo$A$ ikiwa mstatili utaandikwa kwenye mduara wa kitengo$x^2+y^2=1$. Ni uwanja gani wa kuzingatia?

Kidokezo: Ikiwa$(x,y)$ ni vertex ya mraba iliyo katika quadrant ya kwanza, basi eneo la mraba ni$A=(2x)(2y)=4xy.$

Jibu: $A(x)=4x\sqrt{1−x^2}.$Uwanja wa kuzingatia ni$[0,1]$.

Kutatua Matatizo ya Uboreshaji wakati Muda Haufungwa au Haijaingizwa

Katika mifano ya awali, tulizingatia kazi kwenye vikoa vilivyofungwa, vilivyofungwa. Kwa hiyo, kwa theorem ya thamani kali, tulihakikishiwa kuwa kazi zilikuwa na extrema kabisa. Hebu sasa tuchunguze kazi ambazo uwanja haufungwa wala umefungwa.

Kazi nyingi bado zina angalau extrema moja kabisa, hata kama uwanja haujafungwa au uwanja haujafunguliwa. Kwa mfano, kazi$f(x)=x^2+4$ juu$(−∞,∞)$ ina kiwango cha chini kabisa cha$4$ saa$x=0$. Kwa hiyo, bado tunaweza kufikiria kazi juu ya nyanja zisizo na mipaka au vipindi vya wazi na kuamua kama wana extrema yoyote kabisa. Katika mfano unaofuata, tunajaribu kupunguza kazi juu ya uwanja usioingizwa. Tutaona kwamba, ingawa uwanja wa kuzingatia ni$(0,∞),$ kazi ina kiwango cha chini kabisa.

Katika mfano unaofuata, tunaangalia kujenga sanduku la eneo la chini la uso na kiasi kilichowekwa. Si vigumu kuonyesha kwamba kwa sanduku lililofungwa, kwa ulinganifu, kati ya masanduku yote yenye kiasi maalum, mchemraba utakuwa na eneo ndogo zaidi. Kwa hiyo, tunazingatia tatizo lililobadilishwa la kuamua sanduku lililofunguliwa wazi na kiasi maalum kina eneo la uso mdogo zaidi.

Mfano$\PageIndex{6}$: Minimizing Surface Area

Sanduku la mstatili na msingi wa mraba, juu ya wazi, na kiasi cha$216 \,\text{in}^3$ ni kujengwa. Je! Vipimo vya sanduku vinapaswa kupunguza eneo la uso wa sanduku? Eneo la chini la uso ni nini?

Suluhisho

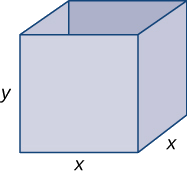
Hatua ya 1: Chora sanduku la mstatili na$x$ uanzishe kutofautiana ili kuwakilisha urefu wa kila upande wa msingi wa mraba; hebu$y$ uwakilisha urefu wa sanduku. Hebu$S$ kuashiria eneo la uso wa sanduku la wazi.

Sanduku yenye msingi wa mraba linaonyeshwa. Msingi una urefu wa upande x, na urefu ni y. — Kielelezo$\PageIndex{8}$: Tunataka kupunguza eneo la uso wa sanduku la mraba na kiasi kilichopewa.

Hatua ya 2: Tunahitaji kupunguza eneo la uso. Kwa hiyo, tunahitaji kupunguza$S$.

Hatua ya 3: Tangu sanduku lina juu ya wazi, tunahitaji tu kuamua eneo la pande nne za wima na msingi. Eneo la kila pande nne za wima ni Eneo$x⋅y.$ la msingi ni$x^2$. Kwa hiyo, eneo la uso wa sanduku ni

$S=4xy+x^2$.

Hatua ya 4: Kwa kuwa kiasi cha sanduku hili ni$x^2y$ na kiasi kinapewa kama$216\,\text{in}^3$, equation kikwazo ni

$x^2y=216$.

Kutatua kikwazo equation kwa$y$, tuna$y=\dfrac{216}{x^2}$. Kwa hiyo, tunaweza kuandika eneo la uso kama kazi ya$x$ tu:

\[S(x)=4x\left(\dfrac{216}{x^2}\right)+x^2.\nonumber \]

Kwa hiyo,$S(x)=\dfrac{864}{x}+x^2$.

Hatua ya 5: Kwa kuwa tunahitaji hilo$x^2y=216$, hatuwezi kuwa nayo$x=0$. Kwa hiyo, tunahitaji$x>0$. Kwa upande mwingine,$x$ anaruhusiwa kuwa na thamani yoyote chanya. Kumbuka kuwa kama$x$ inakuwa kubwa, urefu wa sanduku$y$ unakuwa ndogo sana ili$x^2y=216$. Vile vile, kama$x$ inakuwa ndogo, urefu wa sanduku unakuwa kubwa sana. Tunahitimisha kuwa kikoa ni kipindi cha wazi, kisichoingizwa$(0,∞)$. Kumbuka kwamba, tofauti na mifano ya awali, hatuwezi kupunguza tatizo letu kutafuta kiwango cha juu kabisa au kiwango cha chini kabisa juu ya muda uliofungwa, uliowekwa. Hata hivyo, katika hatua inayofuata, tunagundua kwa nini kazi hii lazima iwe na kiwango cha chini kabisa juu ya muda$(0,∞).$

hatua 6: Kumbuka kuwa kama$x→0^+,\, S(x)→∞.$ Pia, kama$x→∞, \,S(x)→∞$. Kwa kuwa$S$ ni kazi inayoendelea ambayo inakaribia infinity mwisho, ni lazima iwe na kiwango cha chini kabisa katika baadhi$x∈(0,∞)$. Hii kima cha chini lazima kutokea katika hatua muhimu ya$S$. Derivative ni

\[S′(x)=−\dfrac{864}{x^2}+2x.\nonumber \]

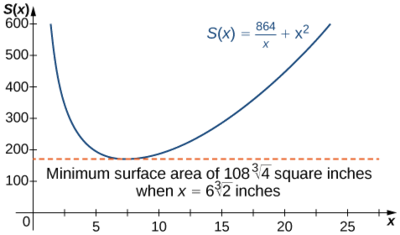
Kwa hiyo,$S′(x)=0$ wakati$2x=\dfrac{864}{x^2}$. Kutatua equation hii kwa$x$, sisi kupata$x^3=432$, hivyo Kwa$x=\sqrt[3]{432}=6\sqrt[3]{2}.$ kuwa hii ni muhimu tu hatua ya$S$, kiwango cha chini kabisa lazima kutokea katika$x=6\sqrt[3]{2}$ (tazama Kielelezo$\PageIndex{9}$).

Wakati$x=6\sqrt[3]{2}$,$y=\dfrac{216}{(6\sqrt[3]{2})^2}=3\sqrt[3]{2}\,\text{in.}$ Kwa hiyo, vipimo vya sanduku lazima$x=6\sqrt[3]{2}\,\text{in.}$ na$y=3\sqrt[3]{2}\,\text{in.}$ Kwa vipimo hivi, eneo la uso ni

\[S(6\sqrt[3]{2})=\dfrac{864}{6\sqrt[3]{2}}+(6\sqrt[3]{2})^2=108\sqrt[3]{4}\,\text{in}^2\nonumber \]

Kazi S (x) = 864/x + x2 ni graphiced. Kwa kiwango cha chini chake kuna mstari na maandishi yaliyopigwa ambayo inasoma “Eneo la chini la uso ni mara 108 mzizi wa mchemraba wa inchi 4 za mraba wakati x = mara 6 mzizi wa mchemraba wa inchi 2.” — Kielelezo$\PageIndex{9}$: Tunaweza kutumia grafu kuamua vipimo vya sanduku la kupewa kiasi na eneo la chini la uso.

Zoezi$\PageIndex{6}$

Fikiria sanduku moja la juu la wazi, ambalo lina kiasi$216\,\text{in}^3$. Tuseme gharama ya vifaa kwa msingi ni$20¢/\text{in}^2$ na gharama ya vifaa kwa pande ni$30¢/\text{in}^2$ na tunajaribu kupunguza gharama ya sanduku hili. Andika gharama kama kazi ya urefu wa upande wa msingi. (Hebu$x$ uwe urefu wa upande wa msingi na$y$ uwe urefu wa sanduku.)

Kidokezo: Kama gharama ya moja ya pande ni gharama$30¢/\text{in}^2,$ ya upande huo ni$0.30xy$ dola.

Jibu: $c(x)=\dfrac{259.2}{x}+0.2x^2$dola

Dhana muhimu

Ili kutatua tatizo la uboreshaji, kuanza kwa kuchora picha na kuanzisha vigezo.
Kupata equation zinazohusiana vigezo.
Kupata kazi ya variable moja kuelezea wingi kwamba ni kuwa kupunguzwa au maximized.
Angalia kwa pointi muhimu Machapisho extrema mitaa.

faharasa

matatizo ya uboreshaji: matatizo ambayo yanatatuliwa kwa kutafuta thamani ya kiwango cha juu au cha chini cha kazi

Mfano\(\PageIndex{1}\): Maximizing the Area of a Garden

Zoezi\(\PageIndex{1}\)

Mkakati wa Kutatua Matatizo: Kutatua Matatizo ya Biashara

Mfano\(\PageIndex{2}\): Maximizing the Volume of a Box

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{3}\): Minimizing Travel Time

Zoezi\(\PageIndex{3}\)

Mfano\(\PageIndex{4}\): Maximizing Revenue

Zoezi\(\PageIndex{4}\)

Mfano\(\PageIndex{5}\): Maximizing the Area of an Inscribed Rectangle

Zoezi\(\PageIndex{5}\)

Mfano\(\PageIndex{6}\): Minimizing Surface Area

Zoezi\(\PageIndex{6}\)