4.6: Mipaka katika Infinity na Asymptotes
- Page ID
- 178875
- Mahesabu ya kikomo ya kazi kama\(x\) ongezeko au itapungua bila amefungwa.
- Tambua asymptote ya usawa kwenye grafu ya kazi.
- Tathmini tabia ya mwisho ya kazi kama\(x\) ongezeko au itapungua bila amefungwa.
- Tambua asymptote ya oblique kwenye grafu ya kazi.
- Kuchambua kazi na derivatives yake kuteka grafu yake.
Tumeonyesha jinsi ya kutumia derivatives ya kwanza na ya pili ya kazi kuelezea sura ya grafu. Ili kuchora kazi\(f\) iliyoelezwa kwenye uwanja usio na mipaka, tunahitaji pia kujua tabia ya\(f\) kama\(x→±∞\). Katika sehemu hii, sisi kufafanua mipaka katika infinity na kuonyesha jinsi mipaka hii kuathiri graph ya kazi. Mwishoni mwa sehemu hii, tunaelezea mkakati wa kuchora kazi ya kiholela\(f\).
Tunaanza kwa kuchunguza nini maana kwa ajili ya kazi ya kuwa na kikomo mwisho katika infinity. Kisha sisi kujifunza wazo la kazi na kikomo usio katika infinity. Nyuma katika Utangulizi wa Kazi na Grafu, tuliangalia asymptotes wima; katika sehemu hii tunahusika na asymptotes ya usawa na oblique.
Mipaka katika Infinity na Ulalo Asymptotes
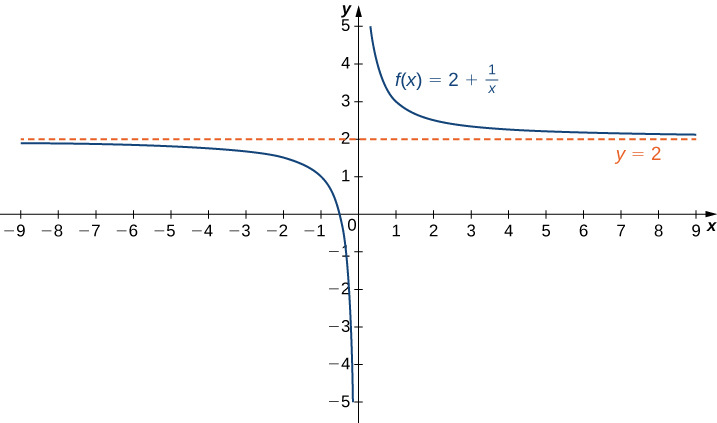
Kumbuka kwamba\(\displaystyle \lim_{x→a}f(x)=L\) ina maana\(f(x)\) inakuwa kiholela karibu\(L\) na muda mrefu kama\(x\) ni kutosha karibu na\(a\). Tunaweza kupanua wazo hili kwa mipaka katika infinity. Kwa mfano, fikiria kazi\(f(x)=2+\frac{1}{x}\). Kama inavyoonekana graphically katika Kielelezo\(\PageIndex{1}\) na numerically katika Jedwali\(\PageIndex{1}\), kama maadili ya\(x\) kupata kubwa, maadili ya\(f(x)\) mbinu\(2\). Tunasema kikomo kama\(x\) mbinu\(∞\) ya\(f(x)\) ni\(2\) na kuandika\(\displaystyle \lim_{x→∞}f(x)=2\). Vile vile\(x<0\), kwa, kama maadili\(|x|\) yanapata kubwa, maadili ya\(f(x)\) mbinu\(2\). Tunasema kikomo kama\(x\) mbinu\(−∞\) ya\(f(x)\) ni\(2\) na kuandika\(\displaystyle \lim_{x→−∞}f(x)=2\).
| \(x\) | 10 | 100 | 1,000 | 10,000 |
|---|---|---|---|---|
| \(2+\frac{1}{x}\) | 2.1 | 2.01 | 2.001 | 2.0001 |
| \(x\) | -10 | -100 | -1000 | -10,000 |
| \(2+\frac{1}{x}\) | 1.9 | 1.99 | 1.999 | 1.9999 |
Kwa ujumla, kwa kazi yoyote\(f\), tunasema kikomo kama\(x→∞\) ya\(f(x)\) ni\(L\) kama\(f(x)\) inakuwa kiholela karibu na muda mrefu\(L\) kama\(x\) ni kutosha kubwa. Katika kesi hiyo, tunaandika\(\displaystyle \lim_{x→∞}f(x)=L\). Vile vile, tunasema kikomo kama\(x→−∞\) ya\(f(x)\) ni\(L\) kama\(f(x)\) inakuwa kiholela karibu na kwa muda mrefu\(L\) kama\(x<0\) na\(|x|\) ni kubwa ya kutosha. Katika kesi hiyo, tunaandika\(\displaystyle \lim_{x→−∞}f(x)=L\). Sasa tunaangalia ufafanuzi wa kazi kuwa na kikomo katika infinity.
Kama maadili ya\(f(x)\) kuwa kiholela karibu na\(L\) kama\(x\) inakuwa kutosha kubwa, tunasema kazi\(f\) ina kikomo katika infinity na kuandika
\[\lim_{x→∞}f(x)=L. \nonumber \]
Kama maadili ya\(f(x)\) inakuwa kiholela karibu na\(L\) kwa\(x<0\) kama\(|x|\) inakuwa kutosha kubwa, tunasema kwamba kazi\(f\) ina kikomo katika infinity hasi na kuandika
\[\lim_{x→−∞}f(x)=L. \nonumber \]
Ikiwa maadili\(f(x)\) yanapata kiholela karibu na thamani ya mwisho\(L\) kama\(x→∞\) au\(x→−∞\), grafu ya\(f\) inakaribia mstari\(y=L\). Katika kesi hiyo, mstari\(y=L\) ni asymptote ya usawa ya\(f\) (Kielelezo\(\PageIndex{2}\)). Kwa mfano, kwa kazi\(f(x)=\dfrac{1}{x}\), tangu\(\displaystyle \lim_{x→∞}f(x)=0\), mstari\(y=0\) ni asymptote ya usawa ya\(f(x)=\dfrac{1}{x}\).

Ikiwa\(\displaystyle \lim_{x→∞}f(x)=L\) au\(\displaystyle \lim_{x→−∞}f(x)=L\), tunasema mstari\(y=L\) ni asymptote ya usawa ya\(f\).
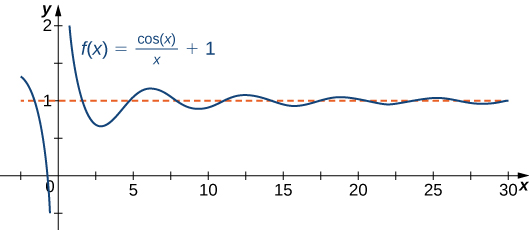
Kazi haiwezi kuvuka asymptote wima kwa sababu grafu lazima ifikie infinity (au\( −∞\)) kutoka angalau mwelekeo mmoja kama\(x\) inakaribia asymptote wima. Hata hivyo, kazi inaweza kuvuka asymptote ya usawa. Kwa kweli, kazi inaweza kuvuka asymptote ya usawa idadi isiyo na ukomo wa nyakati. Kwa mfano, kazi\(f(x)=\dfrac{\cos x}{x}+1\) inavyoonekana katika Kielelezo\(\PageIndex{3}\) intersects asymptote usawa idadi\(y=1\) usio wa nyakati kama oscillates karibu asymptote na amplitude milele-kupungua.
sheria algebraic kikomo na itapunguza theorem sisi kuletwa katika Utangulizi wa Mipaka pia kuomba mipaka katika infinity. Sisi kuonyesha jinsi ya kutumia sheria hizi kukokotoa mipaka kadhaa katika infinity.
Kwa kila moja ya kazi zifuatazo\(f\), tathmini\(\displaystyle \lim_{x→∞}f(x)\) na\(\displaystyle \lim_{x→−∞}f(x)\). Tambua asymptote ya usawa (s) kwa\(f\).
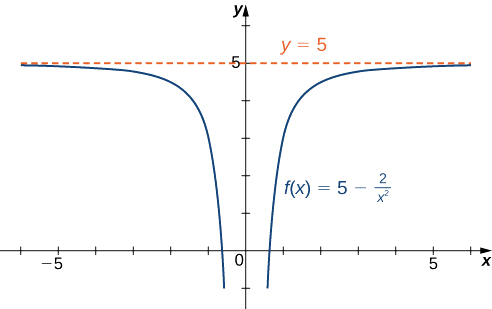
- \(f(x)=5−\dfrac{2}{x^2}\)
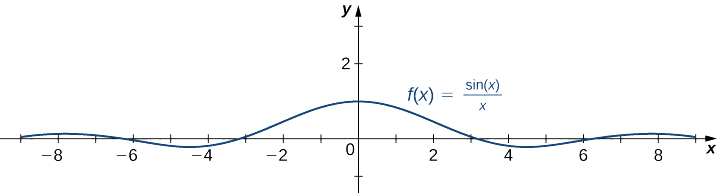
- \(f(x)=\dfrac{\sin x}{x}\)
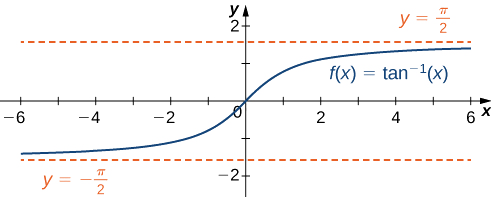
- \(f(x)=\tan^{−1}(x)\)
Suluhisho
kutumia sheria algebraic kikomo, tuna
\[\lim_{x→∞}\left(5−\frac{2}{x^2}\right)=\lim_{x→∞}5−2\left(\lim_{x→∞}\frac{1}{x}\right)\cdot\left(\lim_{x→∞}\frac{1}{x}\right)=5−2⋅0=5.\nonumber \]
Vile vile,\(\displaystyle \lim_{x→−∞}f(x)=5\). Kwa hiyo,\(f(x)=5-\dfrac{2}{x^2}\) ina asymptote usawa wa\(y=5\) na\(f\) mbinu asymptote hii usawa\(x→±∞\) kama inavyoonekana katika grafu zifuatazo.
b Tangu\(-1≤\sin x≤1\) kwa wote\(x\), tuna
\[\frac{−1}{x}≤\frac{\sin x}{x}≤\frac{1}{x}\nonumber \]
kwa ajili ya wote\(x≠0\). Pia, tangu
\(\displaystyle \lim_{x→∞}\frac{−1}{x}=0=\lim_{x→∞}\frac{1}{x}\),
tunaweza kutumia theorem itapunguza kuhitimisha kwamba
\(\displaystyle \lim_{x→∞}\frac{\sin x}{x}=0.\)
Vile vile,
\(\displaystyle \lim_{x→−∞}\frac{\sin x}{x}=0.\)
Hivyo,\(f(x)=\dfrac{\sin x}{x}\) ina asymptote usawa wa\(y=0\) na\(f(x)\) mbinu asymptote hii usawa\(x→±∞\) kama inavyoonekana katika grafu zifuatazo.
c Ili kutathmini\(\displaystyle \lim_{x→∞}\tan^{−1}(x)\) na\(\displaystyle \lim_{x→−∞}\tan^{−1}(x)\), sisi kwanza tunazingatia grafu ya\(y=\tan(x)\) zaidi ya muda\(\left(−\frac{π}{2},\frac{π}{2}\right)\) kama inavyoonekana kwenye grafu ifuatayo.
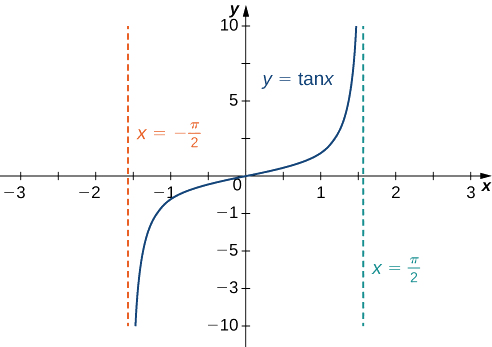
Tangu
\(\displaystyle \lim_{x→\tfrac{π}{2}^−}\tan x=∞,\)
inafuata kwamba
\(\displaystyle \lim_{x→∞}\tan^{−1}(x)=\frac{π}{2}.\)
Vile vile, tangu
\(\displaystyle \lim_{x→-\tfrac{π}{2}^+}\tan x=−∞,\)
inafuata kwamba
\(\displaystyle \lim_{x→−∞}\tan^{−1}(x)=−\frac{π}{2}.\)
Matokeo yake,\(y=\frac{π}{2}\) na\(y=−\frac{π}{2}\) ni asymptotes usawa wa\(f(x)=\tan^{−1}(x)\) kama inavyoonekana katika grafu ifuatayo.
Tathmini\(\displaystyle \lim_{x→−∞}\left(3+\frac{4}{x}\right)\) na\(\displaystyle \lim_{x→∞}\left(3+\dfrac{4}{x}\right)\). Kuamua asymptotes ya usawa ya\(f(x)=3+\frac{4}{x},\) kama ipo.
- Kidokezo
-
\(\displaystyle \lim_{x→±∞}\frac{1}{x}=0\)
- Jibu
-
Mipaka yote ni\(3.\) Mstari\(y=3\) ni asymptote ya usawa.
Mipaka usio katika Infinity
Wakati mwingine maadili ya kazi\(f\) huwa kiholela kubwa kama\(x→∞ \) (au kama\(x→−∞\)). Katika kesi hii, tunaandika\(\displaystyle \lim_{x→∞}f(x)=∞\) (au\(\displaystyle \lim_{x→−∞}f(x)=∞\)). Kwa upande mwingine, kama maadili ya\(f\) ni hasi lakini kuwa kiholela kubwa katika ukubwa kama\(x→∞\) (au kama\(x→−∞\)), sisi kuandika\(\displaystyle \lim_{x→∞}f(x)=−∞\) (au\(\displaystyle \lim_{x→−∞}f(x)=−∞\)).
Kwa mfano, fikiria kazi\(f(x)=x^3\). Kama inavyoonekana katika Jedwali\(\PageIndex{2}\) na Kielelezo\(\PageIndex{8}\), kama\(x→∞\) maadili\(f(x)\) kuwa kiholela kubwa. Kwa hiyo,\(\displaystyle \lim_{x→∞}x^3=∞\). Kwa upande mwingine, kama\(x→−∞\), maadili ya\(f(x)=x^3\) ni hasi lakini kuwa kiholela kubwa katika ukubwa. Kwa hiyo,\(\displaystyle \lim_{x→−∞}x^3=−∞.\)
| \(x\) | 10 | 20 | 50 | 100 | 1000 |
|---|---|---|---|---|---|
| \(x^3\) | 1000 | 8000 | 125,000 | 1,000,000 | 1,000,000,000 |
| \(x\) | -10 | -20 | -50 | -100 | -1000 |
| \(x^3\) | -1000 | -8000 | -125,000 | -1,000,000 | -1,000,000,000 |
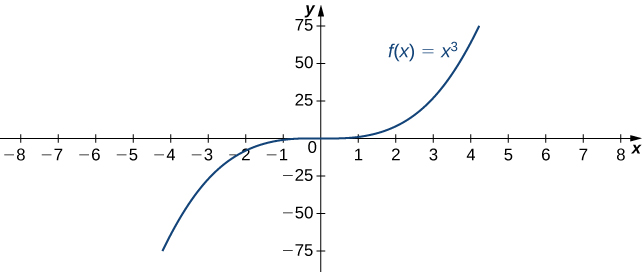
Tunasema kazi\(f\) ina kikomo usio katika infinity na kuandika
\[\lim_{x→∞}f(x)=∞. \nonumber \]
ikiwa\(f(x)\) inakuwa kiholela kikubwa kwa\(x\) kutosha kubwa. Tunasema kazi ina kikomo hasi usio katika infinity na kuandika
\[\lim_{x→∞}f(x)=−∞. \nonumber \]
ikiwa\(f(x)<0\) na\(|f(x)|\) inakuwa kiholela kubwa kwa\(x\) kutosha kubwa. Vile vile, tunaweza kufafanua mipaka usio kama\(x→−∞.\)
Ufafanuzi rasmi
Mapema, tulitumia maneno kwa karibu, kwa kiasi kikubwa, na kwa kutosha kubwa ili kufafanua mipaka kwa infinity isiyo rasmi. Ingawa masharti haya kutoa maelezo sahihi ya mipaka katika infinity, wao si sahihi hesabu. Hapa ni zaidi rasmi ufafanuzi wa mipaka katika infinity. Sisi kisha kuangalia jinsi ya kutumia ufafanuzi huu kuthibitisha matokeo yanayohusisha mipaka katika infinity.
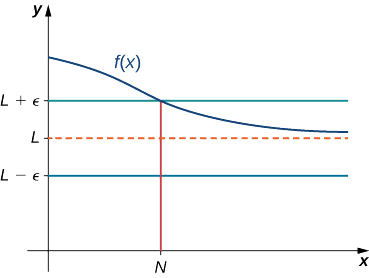
Tunasema kazi\(f\) ina kikomo katika infinity, kama kuna idadi halisi\(L\) kama kwamba kwa ajili ya wote\(ε>0\), kuna\(N>0\) vile kwamba
\[|f(x)−L|<ε \nonumber \]
kwa wote\(x>N.\) katika kesi hiyo, tunaandika
\[\lim_{x→∞}f(x)=L \nonumber \]
Mapema katika sehemu hii, sisi kutumika ushahidi graphical katika Kielelezo\(\PageIndex{1}\) na ushahidi namba katika Jedwali\(\PageIndex{1}\) kuhitimisha kwamba\(\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2\). Hapa tunatumia ufafanuzi rasmi wa kikomo katika infinity kuthibitisha matokeo haya kwa ukali.
Kutumia ufafanuzi rasmi wa kikomo katika infinity kuthibitisha kwamba\(\displaystyle \lim_{x→∞}\left(2+\frac{1}{x}\right)=2\).
Suluhisho
\(ε>0.\)Hebu\(N=\frac{1}{ε}\). Kwa hiyo, kwa wote\(x>N\), tuna
\[\left|2+\frac{1}{x}−2\right|=\left|\frac{1}{x}\right|=\frac{1}{x}<\frac{1}{N}=ε \nonumber \]
Kutumia ufafanuzi rasmi wa kikomo katika infinity kuthibitisha kwamba\(\displaystyle \lim_{x→∞}\left(3-\frac{1}{x^2}\right)=3\).
- Kidokezo
-
Hebu\(N=\frac{1}{\sqrt{ε}}\).
- Jibu
-
\(ε>0.\)Hebu\(N=\frac{1}{\sqrt{ε}}\). Kwa hiyo, kwa wote\(x>N,\) tuna
\[\Big|3−\frac{1}{x^2}−3\Big|=\frac{1}{x^2}<\frac{1}{N^2}=ε \nonumber \]
Kwa hiyo,\(\displaystyle \lim_{x→∞}(3−1/x^2)=3.\)
Sasa tunageuka mawazo yetu kwa ufafanuzi sahihi zaidi kwa kikomo cha usio na mwisho.
Tunasema kazi\(f\) ina kikomo usio katika infinity na kuandika
\(\displaystyle \lim_{x→∞}f(x)=∞\)
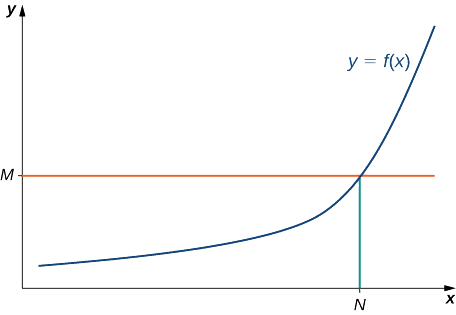
ikiwa kwa wote\(M>0,\) kuna\(N>0\) vile vile
\(f(x)>M\)
kwa wote\(x>N\) (angalia Kielelezo\(\PageIndex{10}\)).
Tunasema kazi ina kikomo hasi usio katika infinity na kuandika
\(\displaystyle \lim_{x→∞}f(x)=−∞\)
kama kwa ajili ya wote\(M<0\), kuna\(N>0\) vile kwamba
\(f(x)<M\)
kwa ajili ya wote\(x>N\).
Vile vile tunaweza kufafanua mipaka kama\(x→−∞.\)
Mapema, tulitumia ushahidi wa picha (Kielelezo\(\PageIndex{8}\)) na ushahidi wa namba (Jedwali\(\PageIndex{2}\)) ili kuhitimisha\(\displaystyle \lim_{x→∞}x^3=∞\) hilo Hapa tunatumia ufafanuzi rasmi wa kikomo usio na mwisho ili kuthibitisha matokeo hayo.
Kutumia ufafanuzi rasmi wa kikomo usio katika infinity kuthibitisha kwamba\(\displaystyle \lim_{x→∞}x^3=∞.\)
Suluhisho
\(M>0.\)Hebu\(N=\sqrt[3]{M}\). Basi, kwa ajili ya wote\(x>N\), tuna
\(x^3>N^3=(\sqrt[3]{M})^3=M.\)
Kwa hiyo,\(\displaystyle \lim_{x→∞}x^3=∞\).
Kutumia ufafanuzi rasmi wa kikomo usio katika infinity kuthibitisha kwamba\(\displaystyle \lim_{x→∞}3x^2=∞.\)
- Kidokezo
-
Hebu\(N=\sqrt{\frac{M}{3}}\).
- Jibu
-
\(M>0.\)Hebu\(N=\sqrt{\frac{M}{3}}\). Basi, kwa ajili ya wote\(x>N,\) tuna
\(3x^2>3N^2=3\left(\sqrt{\frac{M}{3}}\right)^2=\frac{3M}{3}=M\)
Mwisho Tabia
tabia ya kazi kama\(x→±∞\) inaitwa kazi ya mwisho tabia. Katika kila mwisho wa kazi, kazi inaweza kuonyesha moja ya aina zifuatazo za tabia:
- Kazi\(f(x)\) inakaribia asymptote ya usawa\(y=L\).
- Kazi\(f(x)→∞\) au\(f(x)→−∞.\)
- Kazi haipatikani kikomo cha mwisho, wala haifai\(∞\) au\(−∞\). Katika kesi hii, kazi inaweza kuwa na tabia fulani ya oscillatory.
Hebu fikiria madarasa kadhaa ya kazi hapa na angalia aina tofauti za tabia za mwisho kwa kazi hizi.
Mwisho Tabia kwa Kazi Polynomial
Fikiria kazi ya nguvu\(f(x)=x^n\) ambapo\(n\) ni integer chanya. Kutoka Kielelezo\(\PageIndex{11}\) na Kielelezo\(\PageIndex{12}\), tunaona kwamba
\[\lim_{x→∞}x^n=∞;\;n=1,2,3,… \nonumber \]
na
\[\lim_{x→−∞}x^n=\begin{cases}∞, & n=2,4,6,…\\−∞, & n=1,3,5,….\end{cases} \nonumber \]
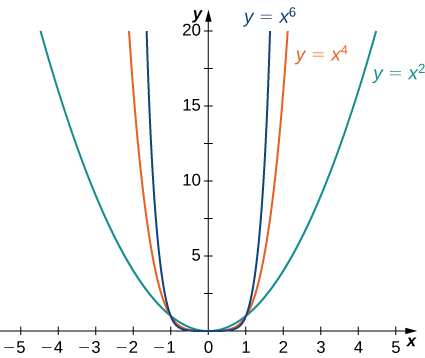
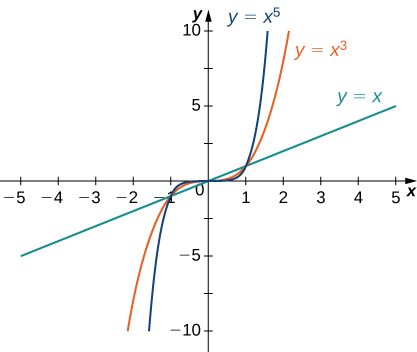
Kutumia ukweli huu, si vigumu kutathmini\(\displaystyle \lim_{x→∞}cx^n\) na\(\displaystyle \lim_{x→−∞}cx^n\), wapi\(c\) mara kwa mara na\(n\) ni integer chanya. Kama\(c>0\), grafu ya\(y=cx^n\) ni kunyoosha wima au compression ya\(y=x^n,\) na kwa hiyo
\(\displaystyle \lim_{x→∞}cx^n=\lim_{x→∞}x^n\)na\(\displaystyle \lim_{x→−∞}cx^n=\lim_{x→−∞}x^n\) kama\(c>0\).
Ikiwa grafu\(c<0,\) ya\(y=cx^n\) ni kunyoosha wima au compression pamoja na kutafakari kuhusu\(x\) -axis, na kwa hiyo
\(\displaystyle \lim_{x→∞}cx^n=−\lim_{x→∞}x^n\)na\(\displaystyle \lim_{x→−∞}cx^n=−\lim_{x→−∞}x^n\) kama\(c<0.\)
Ikiwa\(c=0,y=cx^n=0,\) katika kesi ambayo\(\displaystyle \lim_{x→∞}cx^n=0=\lim_{x→−∞}cx^n.\)
Kwa kila kazi\(f\), tathmini\(\displaystyle \lim_{x→∞}f(x)\) na\(\displaystyle \lim_{x→−∞}f(x)\).
- \(f(x)=−5x^3\)
- \(f(x)=2x^4\)
Suluhisho
- Kwa kuwa mgawo wa\(x^3\) ni\(−5\), grafu ya\(f(x)=−5x^3\) inahusisha kunyoosha wima na kutafakari grafu ya\(y=x^3\) kuhusu\(x\) -axis. Kwa hiyo,\(\displaystyle \lim_{x→∞}(−5x^3)=−∞\) na\(\displaystyle \lim_{x→−∞}(−5x^3)=∞\).
- Tangu mgawo wa\(x^4\) ni\(2\), grafu ya\(f(x)=2x^4\) ni kunyoosha wima ya grafu ya\(y=x^4\). Kwa hiyo,\(\displaystyle \lim_{x→∞}2x^4=∞\) na\(\displaystyle \lim_{x→−∞}2x^4=∞\).
Hebu\(f(x)=−3x^4\). Kupata\(\displaystyle \lim_{x→∞}f(x)\).
- Kidokezo
-
Mgawo\(−3\) ni hasi.
- Jibu
-
\(−∞\)
Sasa tunaangalia jinsi mipaka ya infinity kwa kazi za nguvu inaweza kutumika kuamua\(\displaystyle \lim_{x→±∞}f(x)\) kwa kazi yoyote ya polynomial\(f\). Fikiria kazi ya polynomial
\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a^1x+a^0 \nonumber \]
ya shahada\(n≥1\) ili\(a_n≠0.\)
Factoring, tunaona kwamba
\[f(x)=a_nx^n\left(1+\frac{a_{n−1}}{a_n}\frac{1}{x}+…+\frac{a_1}{a_n}\frac{1}{x^{n−1}}+\frac{a_0}{a_n}\frac{1}{x^n}\right). \nonumber \]
Kama maneno\(x→±∞,\) yote ndani ya mabano yanakaribia sifuri isipokuwa muda wa kwanza. Tunahitimisha kwamba
\[\lim_{x→±∞}f(x)=\lim_{x→±∞}a_nx^n. \nonumber \]
Kwa mfano, kazi\(f(x)=5x^3−3x^2+4\) hufanya kama\(g(x)=5x^3\)\(x→±∞\) ilivyoonyeshwa kwenye Kielelezo\(\PageIndex{13}\) na Jedwali\(\PageIndex{3}\).
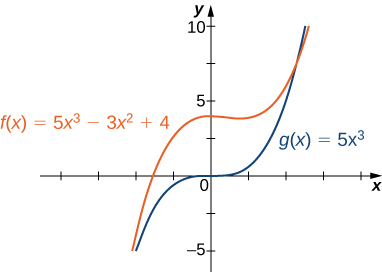
| \(x\) | 10 | 100 | 1000 |
|---|---|---|---|
| \(f(x)=5x^3−3x^2+4\) | 4704 | 4,970,004 | 4,997,000,004 |
| \(g(x)=5x^3\) | 5000 | 5,000,000 | 5,000,000,000 |
| \(x\) | -10 | -100 | -000 |
| \(f(x)=5x^3−3x^2+4\) | -5296 | -5,029,996 | -5,002,999,996 |
| \(g(x)=5x^3\) | -5000 | -5,000,000 | -5,000,000,000 |
Mwisho Tabia kwa Kazi Algebraic
Tabia ya mwisho kwa kazi za busara na kazi zinazohusisha radicals ni ngumu zaidi kuliko kwa polynomials. Katika Mfano\(\PageIndex{5}\), tunaonyesha kwamba mipaka ya infinity ya kazi ya busara\(f(x)=\dfrac{p(x)}{q(x)}\) inategemea uhusiano kati ya kiwango cha nambari na kiwango cha denominator. Ili kutathmini mipaka kwa infinity kwa kazi ya busara, tunagawanya nambari na denominator kwa nguvu ya juu ya\(x\) kuonekana katika denominator. Hii huamua ambayo mrefu katika kujieleza kwa ujumla dominates tabia ya kazi katika maadili kubwa ya\(x\).
Kwa kila moja ya kazi zifuatazo, kuamua mipaka kama\(x→∞\) na\(x→−∞.\) Kisha, kutumia habari hii kuelezea tabia ya mwisho ya kazi.
- \(f(x)=\dfrac{3x−1}{2x+5}\)(Kumbuka: Kiwango cha nambari na denominator ni sawa.)
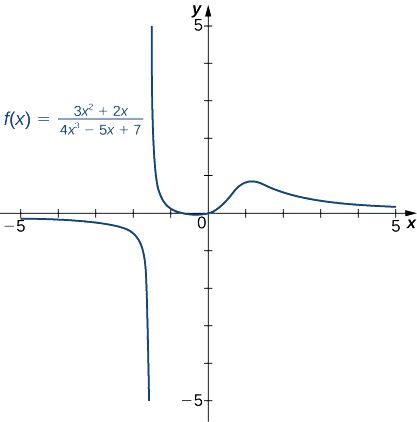
- \(f(x)=\dfrac{3x^2+2x}{4x^3−5x+7}\)(Kumbuka: Kiwango cha nambari ni chini ya kiwango cha denominator.)
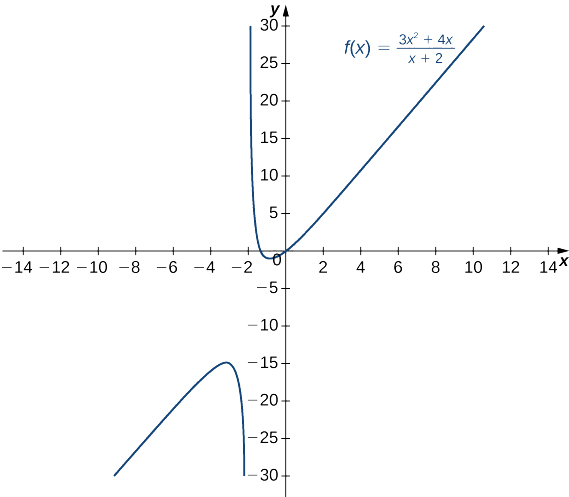
- \(f(x)=\dfrac{3x^2+4x}{x+2}\)(Kumbuka: Kiwango cha nambari ni kubwa kuliko kiwango cha denominator.)
Suluhisho
a. nguvu ya juu ya\(x\) katika denominator ni\(x\). Kwa hiyo, kugawanya nambari na denominator\(x\) na kutumia sheria za kikomo cha algebraic, tunaona kwamba
\[ \begin{align*} \lim_{x→±∞}\frac{3x−1}{2x+5} &=\lim_{x→±∞}\frac{3−1/x}{2+5/x} \\[4pt] &=\frac{\lim_{x→±∞}(3−1/x)}{\lim_{x→±∞}(2+5/x)} \\[4pt] &=\frac{\lim_{x→±∞}3−\lim_{x→±∞}1/x}{\lim_{x→±∞}2+\lim_{x→±∞}5/x} \\[4pt] &=\frac{3−0}{2+0}=\frac{3}{2}. \end{align*}\]
Tangu\(\displaystyle \lim_{x→±∞}f(x)=\frac{3}{2}\), tunajua kwamba\(y=\frac{3}{2}\) ni asymptote usawa kwa kazi hii kama inavyoonekana katika grafu ifuatayo.
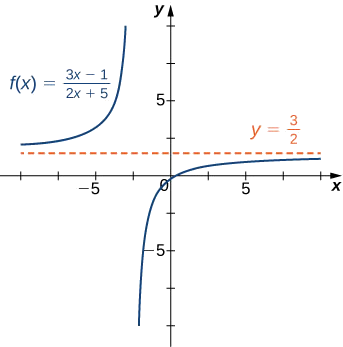
b Kwa kuwa nguvu kubwa ya\(x\) kuonekana katika denominator ni\(x^3\), kugawanya nambari na denominator na\(x^3\). Baada ya kufanya hivyo na kutumia sheria algebraic kikomo, sisi kupata
\[\lim_{x→±∞}\frac{3x^2+2x}{4x^3−5x+7}=\lim_{x→±∞}\frac{3/x+2/x^2}{4−5/x^2+7/x^3}=\frac{3\cdot 0+2\cdot 0}{4−5\cdot 0+7\cdot 0}=\frac{0}{4}=0. \nonumber \]
Kwa hiyo\(f\) ina asymptote usawa wa\(y=0\) kama inavyoonekana katika grafu ifuatayo.
c Kugawanya nambari na denominator na\(x\), tuna
\[\displaystyle \lim_{x→±∞}\frac{3x^2+4x}{x+2}=\lim_{x→±∞}\frac{3x+4}{1+2/x}. \nonumber \]
Kama\(x→±∞\), denominator inakaribia\(1\). Kama\(x→∞\), namba inakaribia\(+∞\). Kama\(x→−∞\), namba inakaribia\(−∞\). Kwa hiyo\(\displaystyle \lim_{x→∞}f(x)=∞\), wakati\(\displaystyle \lim_{x→−∞}f(x)=−∞\) kama inavyoonekana katika takwimu zifuatazo.
Kutathmini\(\displaystyle \lim_{x→±∞}\frac{3x^2+2x−1}{5x^2−4x+7}\) na kutumia mipaka hii kuamua tabia ya mwisho ya\(f(x)=\dfrac{3x^2+2x−1}{5x^2−4x+7}\).
- Kidokezo
-
Gawanya nambari na denominator na\(x^2\).
- Jibu
-
\(\frac{3}{5}\)
Kabla ya kuendelea, fikiria grafu ya\(f(x)=\dfrac{3x^2+4x}{x+2}\) inavyoonekana kwenye Kielelezo\(\PageIndex{16}\). Kama\(x→∞\) na\(x→−∞\), grafu ya\(f\) inaonekana karibu linear. Ingawa\(f\) ni hakika si kazi linear, sisi sasa kuchunguza kwa nini grafu ya\(f\) inaonekana kuwa inakaribia kazi linear. Kwanza, kwa kutumia mgawanyiko wa muda mrefu wa polynomials, tunaweza kuandika
\[f(x)=\frac{3x^2+4x}{x+2}=3x−2+\frac{4}{x+2}. \nonumber \]
Tangu\(\dfrac{4}{x+2}→0\) kama\(x→±∞,\) sisi kuhitimisha kwamba
\[ \lim_{x→±∞}(f(x)−(3x−2))=\lim_{x→±∞}\frac{4}{x+2}=0. \nonumber \]
Kwa hiyo, grafu ya\(f\) mbinu line\(y=3x−2\) kama\(x→±∞\). Mstari huu unajulikana kama asymptote ya oblique kwa\(f\) (Kielelezo\(\PageIndex{17}\)).
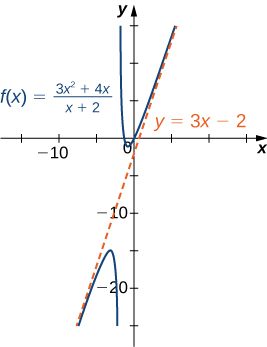
Tunaweza muhtasari matokeo ya Mfano\(\PageIndex{5}\) kufanya hitimisho zifuatazo kuhusu tabia ya mwisho kwa ajili ya kazi ya busara. Fikiria kazi ya busara
\[f(x)=\frac{p(x)}{q(x)}=\frac{a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0}{b_mx^m+b_{m−1}x^{m−1}+…+b_1x+b_0},\nonumber \]
wapi\(a_n≠0\) na\(b_m≠0.\)
- Ikiwa kiwango cha nambari ni sawa na kiwango cha denominator,\((n=m),\) basi\(f\) ina asymptote ya usawa ya\(y=a_n/b_m\) kama\(x→±∞.\)
- Ikiwa kiwango cha nambari ni chini ya kiwango cha denominator\((n<m),\) basi\(f\) ina asymptote ya usawa ya\(y=0\) kama\(x→±∞.\)
- Ikiwa kiwango cha nambari ni kubwa kuliko kiwango cha denominator\((n>m),\) basi\(f\) haina asymptote ya usawa. Mipaka ya infinity ni ama chanya au hasi infinity, kulingana na ishara za maneno ya kuongoza. Aidha, kwa kutumia mgawanyiko wa muda mrefu, kazi inaweza kuandikwa upya kama\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x)}, \nonumber \] ambapo shahada ya\(r(x)\) ni chini ya kiwango cha\(q(x)\). Matokeo yake,\(\displaystyle \lim_{x→±∞}r(x)/q(x)=0\). Kwa hiyo, maadili ya\([f(x)−g(x)]\) mbinu sifuri kama\(x→±∞\). Ikiwa kiwango cha\(p(x)\) ni moja zaidi ya kiwango cha\(q(x)\) (yaani,\(n=m+1\)), kazi\(g(x)\) ni kazi ya mstari. Katika kesi hii, tunaita\(g(x)\) asymptote ya oblique.
Sasa hebu fikiria tabia ya mwisho kwa ajili ya kazi zinazohusisha radical.
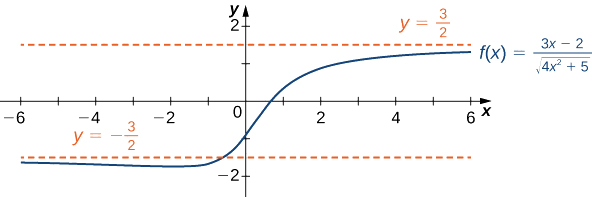
Kupata mipaka kama\(x→∞\) na\(x→−∞\) kwa\(f(x)=\dfrac{3x−2}{\sqrt{4x^2+5}}\) na kuelezea tabia ya mwisho ya\(f\).
Suluhisho
Hebu kutumia mkakati huo kama tulivyofanya kwa kazi za busara: kugawanya nambari na denominator kwa nguvu ya\(x\). Kuamua nguvu sahihi ya\(x\), fikiria maneno\(\sqrt{4x^2+5}\) katika denominator. Tangu
\[\sqrt{4x^2+5}≈\sqrt{4x^2}=2|x| \nonumber \]
kwa maadili makubwa ya\(x\) athari\(x\) inaonekana tu kwa nguvu ya kwanza katika denominator. Kwa hiyo, tunagawanya nambari na denominator na\(|x|\). Kisha, kwa kutumia ukweli kwamba\(|x|=x\)\(x>0, |x|=−x\) kwa\(x<0\), na\(|x|=\sqrt{x^2}\) kwa wote\(x\), tunahesabu mipaka kama ifuatavyo:
\ [kuanza {align*}\ lim_ {x→ Δ}\ frac {3x-1} {\ sqrt {4x^2+5}} &=\ lim_ {x→ Δ}\ frac {(1/|x|) (3x-1)} {(1/|x|)\ sqrt {4x^2+5}}\ [4pt]
&=\ lim_ {x→ Δ}\ frac {(1/x) (3x-1)} {\ sqrt {(1/x^2) (4x^2+5)}}\\ [4pt]
&=\ lim_ {x→ Δ}\ frac {3,12/x} {\ sqrt {4+5/x ^ 2}} =\ frac {3} {\ sqrt {4}} {\ frac {4} {\ frac {4} {\ frac {4} {\ frac {4} {\ sqrt {4} {\ sqrt {4} {\ sqrt {3} {2}\ mwisho {align*}\]
\ [kuanza {align*}\ lim_ {x→ Δ}\ frac {3x-2} {\ sqrt {4x^2+5}} &=\ lim_ {x→ Δ}\ Frac {(1/|x|) (3x-1)} {(1/|x|)\ sqrt {4x^2+5}}\\ [4pt]
&=\ lim_ {x→ Δ}\ frac {(-1/x) (3x-1)} {\ sqrt {(1/x^2) (4x^2+5)}}\\ [4pt]
&=\ lim_ {x→ —Δ}\ frac {-3+2/x} {\ sqrt {4+5/x ^ 2}\ frac {\ sqrt {\ sqrt 4} {\ sqrt {\ sqrt 4}} =\ frac {·3} {2}. \ mwisho {align*}\]
Kwa hiyo,\(f(x)\) inakaribia asymptote ya usawa\(y=\frac{3}{2}\) kama\(x→∞\) na asymptote ya usawa\(y=−\frac{3}{2}\)\(x→−∞\) kama inavyoonekana kwenye grafu ifuatayo.
Tathmini\(\displaystyle \lim_{x→∞}\frac{\sqrt{3x^2+4}}{x+6}\).
- Kidokezo
-
Gawanya nambari na denominator na\(x\).
- Jibu
-
\(\sqrt{3}\)
Kuamua Mwisho Tabia kwa Kazi Transcendental
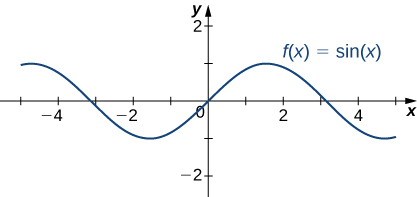
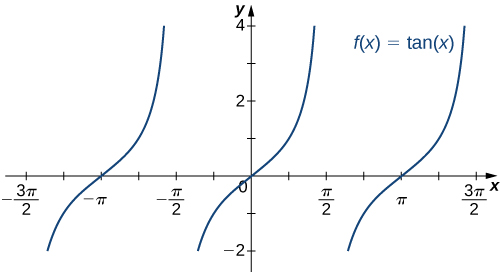
kazi sita za msingi trigonometric ni mara kwa mara na wala mbinu kikomo mwisho kama\(x→±∞.\) Kwa mfano,\(\sin x\) oscillates kati ya 1 na -1 (Kielelezo\(\PageIndex{19}\)). kazi tangent\(x\) ina idadi usio wa asymptotes wima kama\(x→±∞\); Kwa hiyo, haina mbinu kikomo mwisho wala haina mbinu\(±∞\)\(x→±∞\) kama inavyoonekana katika Kielelezo\(\PageIndex{20}\).
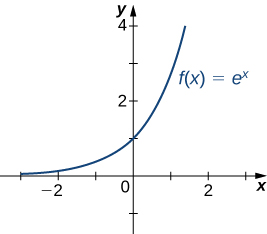
Kumbuka kwamba kwa msingi wowote kazi\(y=b^x\) ni kazi\(b>0,\; b≠1,\) ya kielelezo na kikoa\((−∞,∞)\) na upeo\((0,∞)\). Kama\(b>1,\;y=b^x\) ni kuongeza juu ya\((−∞,∞)\). Kama\(0<b<1, \; y=b^x\) ni kupungua juu ya\((−∞,∞).\) Kwa kazi ya asili kielelezo\(f(x)=e^x, \; e≈2.718>1\). Kwa hiyo,\(f(x)=e^x\) ni kuongeza juu\((−∞,∞)\) na mbalimbali ni\((0,∞)\). Kazi ya kielelezo\(f(x)=e^x\) inakaribia\(∞\) kama\(x→∞\) na mbinu\(0\) kama\(x→−∞\) inavyoonekana katika Jedwali\(\PageIndex{4}\) na Kielelezo\(\PageIndex{21}\).
| \(x\) | -5 | -2 | 0 | 2 | 5 |
|---|---|---|---|---|---|
| \(e^x\) | 0.00674 | 0.135 | 1 | 7.389 | 148.413 |
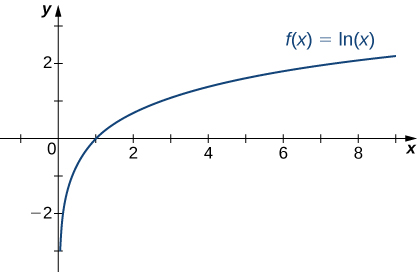
Kumbuka kwamba kazi ya logarithm ya asili\(f(x)=\ln(x)\) ni inverse ya kazi ya asili ya kielelezo\(y=e^x\). Kwa hiyo, uwanja wa\(f(x)=\ln(x)\) ni\((0,∞)\) na upeo ni\((−∞,∞)\). Grafu ya\(f(x)=\ln(x)\) ni kutafakari kwa grafu ya\(y=e^x\) juu ya mstari\(y=x\). Kwa hiyo,\(\ln(x)→−∞\) kama\(x→0^+\) na\(\ln(x)→∞\) kama\(x→∞\) inavyoonekana katika Kielelezo\(\PageIndex{22}\) na Jedwali\(\PageIndex{5}\).
| \(x\) | 0.01 | 0.1 | 1 | 10 | 100 |
|---|---|---|---|---|---|
| \(\ln(x)\) | -4.605 | -2.303 | 0 | 2.303 | 4.605 |
Kupata mipaka kama\(x→∞\) na\(x→−∞\) kwa\(f(x)=\dfrac{2+3e^x}{7−5e^x}\) na kuelezea tabia ya mwisho ya\(f.\)
Suluhisho
Ili kupata kikomo kama\(x→∞,\) kugawanya nambari na denominator na\(e^x\):
\[ \begin{align*} \lim_{x→∞}f(x) &= \lim_{x→∞}\frac{2+3e^x}{7−5e^x} \\[4pt] &=\lim_{x→∞}\frac{(2/e^x)+3}{(7/e^x)−5.} \end{align*}\]
Kama inavyoonekana katika Kielelezo\(\PageIndex{21}\),\(e^x→∞\) kama\(x→∞\). Kwa hiyo,
\(\displaystyle \lim_{x→∞}\frac{2}{e^x}=0=\lim_{x→∞}\frac{7}{e^x}\).
Tunahitimisha kuwa\(\displaystyle \lim_{x→∞}f(x)=−\frac{3}{5}\), na grafu ya\(f\) mbinu asymptote ya usawa\(y=−\frac{3}{5}\) kama\(x→∞.\) Ili kupata kikomo kama\(x→−∞\), tumia ukweli kwamba\(e^x→0\)\(x→−∞\) kuhitimisha kwamba\(\displaystyle \lim_{x→-∞}f(x)=\frac{2}{7}\), na kwa hiyo grafu ya\(f(x)\) inakaribia asymptote ya usawa \(y=\frac{2}{7}\)kama\(x→−∞\).
Kupata mipaka kama\(x→∞\) na\(x→−∞\) kwa\(f(x)=\dfrac{3e^x−4}{5e^x+2}\).
- Kidokezo
-
\(\displaystyle \lim_{x→∞}e^x=∞\)na\(\displaystyle \lim_{x→-∞}e^x=0.\)
- Jibu
-
\(\displaystyle \lim_{x→∞}f(x)=\frac{3}{5}, \quad\lim_{x→−∞}f(x)=−2\)
Miongozo ya Kuchora Grafu ya Kazi
Sasa tuna zana za kutosha za uchambuzi kuteka grafu za aina mbalimbali za kazi za algebraic na transcendental. Kabla ya kuonyesha jinsi ya kuchora kazi maalum, hebu tuangalie mkakati wa jumla wa kutumia wakati wa kuchora kazi yoyote.
Kutokana na kazi\(f\), kutumia hatua zifuatazo kwa mchoro grafu ya\(f\):
- Tambua uwanja wa kazi.
- Pata\(x\) - na\(y\) -intercepts.
- Tathmini\(\displaystyle \lim_{x→∞}f(x)\) na\(\displaystyle \lim_{x→−∞}f(x)\) kuamua tabia ya mwisho. Ikiwa mojawapo ya mipaka hii ni idadi ya mwisho\(L\), basi\(y=L\) ni asymptote ya usawa. Ikiwa mojawapo ya mipaka hii ni\(∞\) au\(−∞\), onyesha ikiwa\(f\) ina asymptote ya oblique. Ikiwa\(f\) ni kazi ya busara kama hiyo\(f(x)=\dfrac{p(x)}{q(x)}\), ambapo kiwango cha nambari ni kubwa kuliko kiwango cha denominator, basi\(f\) inaweza kuandikwa kama\[f(x)=\frac{p(x)}{q(x)}=g(x)+\frac{r(x)}{q(x),} \nonumber \] ambapo kiwango cha\(r(x)\) ni chini ya kiwango cha\(q(x)\). Maadili ya\(f(x)\) mbinu maadili ya\(g(x)\) kama\(x→±∞\). Ikiwa\(g(x)\) ni kazi ya mstari, inajulikana kama asymptote ya oblique.
- Kuamua ikiwa\(f\) ina asymptotes yoyote ya wima.
- Tumia\(f′.\) Pata pointi zote muhimu na ueleze vipindi ambapo\(f\) unaongezeka na wapi\(f\) unapungua. Kuamua kama\(f\) ina extrema yoyote ya ndani.
- Mahesabu\(f''.\) Kuamua vipindi ambapo\(f\) ni concave juu na wapi\(f\) concave chini. Tumia habari hii ili uone ikiwa\(f\) ina pointi yoyote ya kufuta. Derivative ya pili pia inaweza kutumika kama njia mbadala ya kuamua au kuthibitisha kuwa\(f\) ina extremum ya ndani katika hatua muhimu.
Sasa hebu kutumia mkakati huu kwa graph kazi mbalimbali. Tunaanza kwa kuchora kazi ya polynomial.
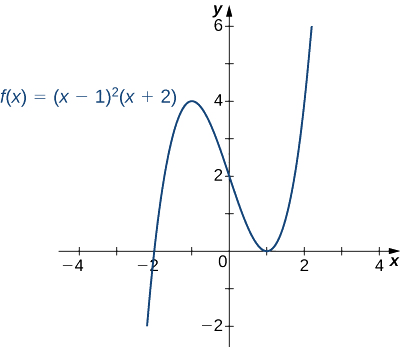
Mchoro grafu ya\(f(x)=(x−1)^2(x+2).\)
Suluhisho
Hatua ya 1: Kwa kuwa\(f\) ni polynomial, uwanja ni seti ya namba zote halisi.
Hatua ya 2: Wakati\(x=0,\; f(x)=2.\) Kwa hiyo,\(y\) -intercept ni\((0,2)\). Ili kupata\(x\) -intercepts, tunahitaji kutatua equation\((x−1)^2(x+2)=0\), ambayo inatupa\(x\) -intercepts\((1,0)\) na\((−2,0)\)
Hatua ya 3: Tunahitaji kutathmini tabia ya mwisho ya\(f.\) As\(x→∞, \;(x−1)^2→∞\) na\((x+2)→∞\). Kwa hiyo,\(\displaystyle \lim_{x→∞}f(x)=∞\).
Kama\(x→−∞, \;(x−1)^2→∞\) na\((x+2)→−∞\). Kwa hiyo,\(\displaystyle \lim_{x→-∞}f(x)=−∞\).
Kupata taarifa zaidi kuhusu tabia ya mwisho ya\(f\), tunaweza kuzidisha sababu za\(f\). Wakati wa kufanya hivyo, tunaona kwamba
\[f(x)=(x−1)^2(x+2)=x^3−3x+2. \nonumber \]
Tangu muda wa kuongoza\(f\) ni\(x^3\), sisi kuhitimisha kwamba\(f\) tabia\(y=x^3\) kama\(x→±∞.\)
Hatua ya 4: Kwa kuwa\(f\) ni kazi ya polynomial, haina asymptotes yoyote ya wima.
Hatua ya 5: derivative kwanza ya\(f\) ni
\[f′(x)=3x^2−3. \nonumber \]
Kwa hiyo,\(f\) ina pointi mbili muhimu:\(x=1,−1.\) Gawanya muda\((−∞,∞)\) katika vipindi vitatu vidogo:\((−∞,−1), \;(−1,1)\), na\((1,∞)\). Kisha, chagua pointi za mtihani\(x=−2, x=0\), na\(x=2\) kutoka kwa vipindi hivi na tathmini ishara ya kila\(f′(x)\) moja ya pointi hizi za mtihani, kama inavyoonekana katika meza ifuatayo.
| Muda | Kipimo cha mtihani | Ishara ya derivative\(f'(x)=3x^2−3=3(x−1)(x+1)\) | Hitimisho |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f' (x) =3x^2,13=3 (x-1) (x+1)\)” style="text-align:center; ">\((+)(−)(−)=+\) | \(f\)inaongezeka |
| \((−1,1)\) | \(x=0\) | \ (f' (x) =3x^2,13=3 (x-1) (x+1)\)” style="text-align:center; ">\((+)(−)(+)=−\) | \(f\)kupungua |
| \((1,∞)\) | \(x=2\) | \ (f' (x) =3x^2,13=3 (x-1) (x+1)\)” style="text-align:center; ">\((+)(+)(+)=+\) | \(f\)inaongezeka |
Kutoka meza, tunaona kwamba\(f\) ina kiwango cha juu ndani katika\(x=−1\) na kiwango cha chini ndani katika\(x=1\). Kutathmini\(f(x)\) katika pointi hizo mbili, tunaona kwamba thamani ya juu ya ndani ni\(f(−1)=4\) na thamani ya chini ya ndani ni\(f(1)=0.\)
Hatua ya 6: derivative pili ya\(f\) ni
\[f''(x)=6x. \nonumber \]
derivative pili ni sifuri katika\(x=0.\) Kwa hiyo, kuamua concavity ya\(f\), kugawanya muda\((−∞,∞)\) katika vipindi vidogo\((−∞,0)\) na\((0,∞)\), na kuchagua pointi mtihani\(x=−1\) na\(x=1\) kuamua concavity ya\(f\) juu ya kila moja ya vipindi hivi vidogo kama inavyoonekana katika meza ifuatayo.
| Muda | Mtihani Point | Ishara ya\(f''(x)=6x\) | Hitimisho |
|---|---|---|---|
| \((−∞,0)\) | \(x=−1\) | \ (f "(x) =6x\)” style="text-align:katikati; ">\(−\) | \(f\)ni concave chini. |
| \((0,∞)\) | \(x=1\) | \ (f "(x) =6x\)” style="text-align:katikati; ">\(+\) | \(f\)ni concave up. |
Tunaona kwamba taarifa katika meza iliyotangulia inathibitisha ukweli, kupatikana katika hatua\(5\), kwamba f ina kiwango cha juu ndani katika\(x=−1\) na kiwango cha chini ndani katika\(x=1\). Kwa kuongeza, maelezo yaliyopatikana katika\(5\) hatua-yaani,\(f\) ina kiwango cha juu cha ndani\(x=−1\) na kiwango cha chini cha ndani\(x=1\), na\(f′(x)=0\) kwa pointi hizo-pamoja na ukweli kwamba\(f''\) mabadiliko ya ishara tu katika\(x=0\) inathibitisha matokeo yaliyopatikana katika hatua\(6\) juu ya concavity ya\(f\).
Kuchanganya habari hii, tunawasili kwenye grafu ya\(f(x)=(x−1)^2(x+2)\) inavyoonekana kwenye grafu ifuatayo.
Mchoro grafu ya\(f(x)=(x−1)^3(x+2).\)
- Kidokezo
-
\(f\)ni polynomial ya shahada ya nne.
- Jibu
-
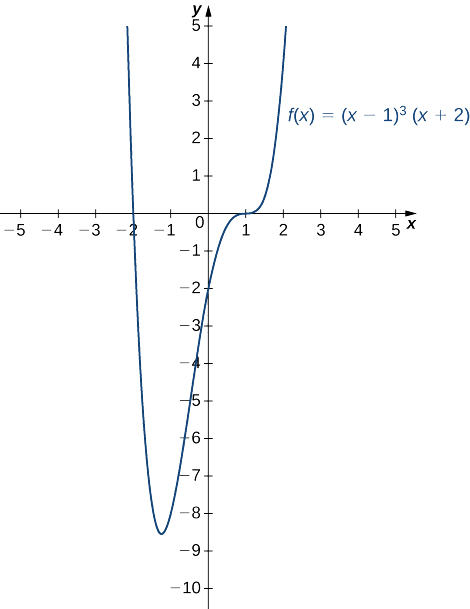
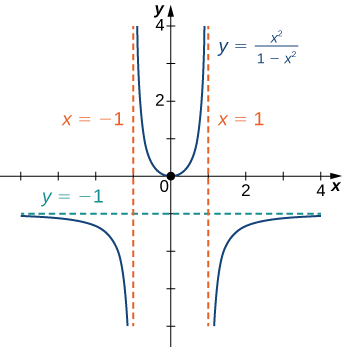
Mchoro grafu ya\(f(x)=\dfrac{x^2}{1−x^2}\).
Suluhisho
Hatua ya 1: Kazi\(f\) hufafanuliwa kwa muda mrefu kama denominator si sifuri. Kwa hiyo, uwanja ni seti ya namba zote halisi\(x\) isipokuwa\(x=±1.\)
Hatua ya 2: Pata intercepts. Kama\(x=0,\) basi\(f(x)=0\), hivyo\(0\) ni intercept. Ikiwa\(y=0\), basi\(\dfrac{x^2}{1−x^2}=0,\) ina maana\(x=0\). Kwa hiyo,\((0,0)\) ni intercept tu.
Hatua ya 3: Tathmini mipaka katika infinity. Kwa kuwa\(f\) ni kazi ya busara, kugawanya nambari na denominator kwa nguvu ya juu katika denominator:\(x^2\) .Tunapata
\(\displaystyle \lim_{x→±∞}\frac{x^2}{1−x^2}=\lim_{x→±∞}\frac{1}{\frac{1}{x^2}−1}=−1.\)
Kwa hiyo,\(f\) ina asymptote ya usawa ya\(y=−1\) kama\(x→∞\) na\(x→−∞.\)
Hatua ya 4: Kuamua ikiwa\(f\) ina asymptotes yoyote ya wima, angalia kwanza ili uone kama denominator ina zero yoyote. Tunapata denominator ni sifuri wakati\(x=±1\). Kuamua kama mistari\(x=1\) au\(x=−1\) ni asymptotes wima ya\(f\), tathmini\(\displaystyle \lim_{x→1}f(x)\) na\(\displaystyle \lim_{x→−1}f(x)\). Kwa kuangalia kila kikomo upande mmoja kama\(x→1,\) tunaona kwamba
\(\displaystyle \lim_{x→1^+}\frac{x^2}{1−x^2}=−∞\)na\(\displaystyle \lim_{x→1^−}\frac{x^2}{1−x^2}=∞.\)
Aidha, kwa kuangalia kila kikomo upande mmoja kama\(x→−1,\) sisi kupata kwamba
\(\displaystyle \lim_{x→−1^+}\frac{x^2}{1−x^2}=∞\)na\(\displaystyle \lim_{x→−1^−}\frac{x^2}{1−x^2}=−∞.\)
Hatua ya 5: Tumia derivative ya kwanza:
\(f′(x)=\dfrac{(1−x^2)(2x)−x^2(−2x)}{\Big(1−x^2\Big)^2}=\dfrac{2x}{\Big(1−x^2\Big)^2}\).
Pointi muhimu hutokea mahali\(x\) ambapo\(f′(x)=0\) au\(f′(x)\) haijulikani. Tunaona kwamba\(f′(x)=0\) wakati\(x=0.\) derivative\(f′\) si undefined wakati wowote katika uwanja wa\(f\). Hata hivyo,\(x=±1\) si katika uwanja wa\(f\). Kwa hiyo, ili kuamua wapi\(f\) inaongezeka na wapi\(f\) unapungua, ugawanye muda\((−∞,∞)\) katika vipindi vinne vidogo:\((−∞,−1), (−1,0), (0,1),\) na\((1,∞)\), na uchague hatua ya mtihani katika kila kipindi ili kuamua ishara ya\(f′(x)\) kila moja ya vipindi hivi. maadili\(x=−2,\; x=−\frac{1}{2}, \;x=\frac{1}{2}\), na\(x=2\) ni uchaguzi mzuri kwa pointi mtihani kama inavyoonekana katika meza ifuatayo.
| Muda | Kipimo cha mtihani | Ishara ya\(f′(x)=\frac{2x}{(1−x^2)^2}\) | Hitimisho |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f′ (x) =\ frac {2x} {(1,1x^2) ^2}\)” style="text-align:katikati; ">\(−/+=−\) | \(f\)inapungua. |
| \((−1,0)\) | \(x=−1/2\) | \ (f′ (x) =\ frac {2x} {(1,1x^2) ^2}\)” style="text-align:katikati; ">\(−/+=−\) | \(f\)inapungua. |
| \((0,1)\) | \(x=1/2\) | \ (f′ (x) =\ frac {2x} {(1,1x^2) ^2}\)” style="text-align:katikati; ">\(+/+=+\) | \(f\)inaongezeka. |
| \((1,∞)\) | \(x=2\) | \ (f′ (x) =\ frac {2x} {(1,1x^2) ^2}\)” style="text-align:katikati; ">\(+/+=+\) | \(f\)inaongezeka. |
Kutokana na uchambuzi huu, tunahitimisha kuwa\(f\) ina kiwango cha chini cha ndani\(x=0\) lakini hakuna upeo wa ndani.
Hatua ya 6: Tumia derivative ya pili:
\ [kuanza {align*} f "(x) &=\ frac {(1,1x^2) ^2 (2) -2x (2 (1,1x^2) (-2x))} {(1,1x^2) ^4}\\ [4pt]
&=\ frac {(1,1-x ^ 2) +8x^2]} {\ Kubwa (1,1x^2\ Big) ^4}\\ [4pt]
&=\ Frac {2 (1,1x^2) +8x^2} {\ Big (1,1x^2\ Big) ^3}\ [4pt]
&=\ frac {6x^2+2} {\ Big (1,1x^2\ Big) ^3}. \ mwisho {align*}\]
Kuamua vipindi ambapo\(f\) ni concave juu na wapi\(f\) concave chini, sisi kwanza haja ya kupata pointi zote\(x\) ambapo\(f''(x)=0\) au\(f''(x)\) haijulikani. Tangu nambari\(6x^2+2≠0\) ya yoyote\(x, f''(x)\) haijawahi sifuri. Zaidi ya hayo,\(f''\) si undefined kwa yeyote\(x\) katika uwanja wa\(f\). Hata hivyo, kama ilivyojadiliwa hapo awali,\(x=±1\) si katika uwanja wa\(f\). Kwa hiyo, kuamua concavity ya\(f\), sisi kugawanya muda\((−∞,∞)\) katika vipindi vitatu vidogo\((−∞,−1), \, (−1,1)\)\((1,∞)\), na, na kuchagua hatua ya mtihani katika kila moja ya vipindi hivi kutathmini ishara ya\(f''(x)\). maadili\(x=−2, \;x=0\), na\(x=2\) inawezekana pointi mtihani kama inavyoonekana katika meza ifuatayo.
| Muda | Mtihani Point | Ishara ya\(f''(x)=\frac{6x^2+2}{(1−x^2)^3}\) | Hitimisho |
|---|---|---|---|
| \((−∞,−1)\) | \(x=−2\) | \ (f "(x) =\ frac {6x^2+2} {(1,1x^2) ^3}\)” style="text-align:katikati; ">\(+/−=−\) | \(f\)ni concave chini. |
| \((−1,1)\) | \(x=0\) | \ (f "(x) =\ frac {6x^2+2} {(1,1x^2) ^3}\)” style="text-align:katikati; ">\(+/+=+\) | \(f\)ni concave up |
| \((1,∞)\) | \(x=2\) | \ (f "(x) =\ frac {6x^2+2} {(1,1x^2) ^3}\)” style="text-align:katikati; ">\(+/−=−\) | \(f\)ni concave chini. |
Kuchanganya habari hii yote, tunawasili kwenye grafu ya\(f\) hapa chini. Kumbuka kwamba, ingawa\(f\) mabadiliko concavity katika\(x=−1\) na\(x=1\), hakuna pointi inflection katika mojawapo ya maeneo haya kwa sababu\(f\) si kuendelea katika\(x=−1\) au\(x=1.\)
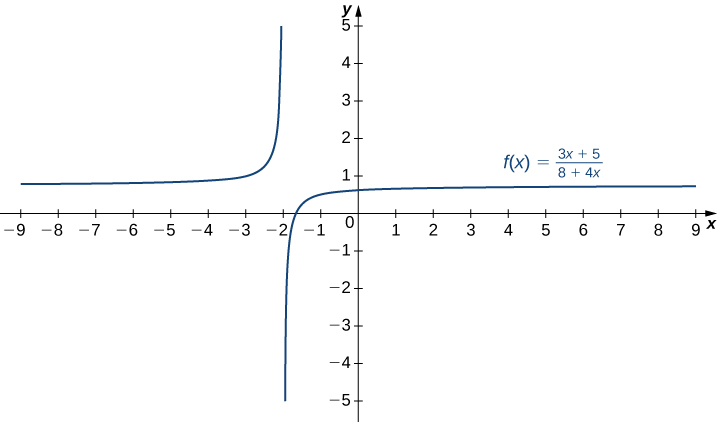
Mchoro grafu ya\(f(x)=\dfrac{3x+5}{8+4x}.\)
- Kidokezo
-
Mstari\(y=L\) ni asymptote usawa wa\(f\) kama kikomo kama\(x→∞\) au kikomo kama\(x→−∞\) ya\(f(x)\) ni\(L\). Mstari\(x=a\) ni asymptote wima ikiwa angalau moja ya mipaka ya upande mmoja wa\(f\) kama\(x→a\) ni\(∞\) au\(−∞.\)
- Jibu
-
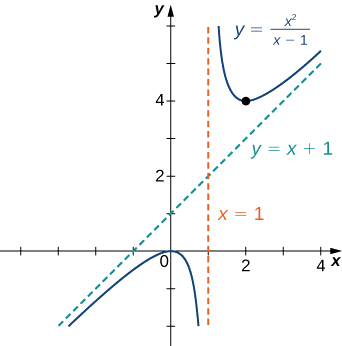
Mchoro grafu ya\(f(x)=\dfrac{x^2}{x−1}\)
Suluhisho
Hatua ya 1: Kikoa cha\(f\) ni seti ya namba zote halisi\(x\) isipokuwa\(x=1.\)
Hatua ya 2: Pata intercepts. Tunaweza kuona kwamba wakati\(x=0, \,f(x)=0,\) hivyo\((0,0)\) ni kukatiza tu.
Hatua ya 3: Tathmini mipaka katika infinity. Kwa kuwa kiwango cha nambari ni moja zaidi ya kiwango cha denominator,\(f\) lazima iwe na asymptote ya oblique. Ili kupata asymptote ya oblique, tumia mgawanyiko mrefu wa polynomials kuandika
\(f(x)=\dfrac{x^2}{x−1}=x+1+\dfrac{1}{x−1}\).
Tangu\(\dfrac{1}{x−1}→0\) kama\(x→±∞, f(x)\) mbinu line\(y=x+1\) kama\(x→±∞\). Mstari\(y=x+1\) ni asymptote ya oblique kwa\(f\).
Hatua ya 4: Kuangalia asymptotes wima, angalia ambapo denominator ni sifuri. Hapa denominator ni sifuri katika\(x=1.\) Kuangalia mipaka yote upande mmoja kama\(x→1,\) sisi kupata
\(\displaystyle \lim_{x→1^+}\frac{x^2}{x−1}=∞\)na\(\displaystyle \lim_{x→1^−}\frac{x^2}{x−1}=−∞.\)
Kwa hiyo,\(x=1\) ni asymptote wima, na tumeamua tabia ya\(f\) kama\(x\) mbinu\(1\) kutoka kulia na kushoto.
Hatua ya 5: Tumia derivative ya kwanza:
\(f′(x)=\dfrac{(x−1)(2x)−x^2(1)}{(x−1)^2}=\dfrac{x^2−2x}{(x−1)^2}.\)
Tuna\(f′(x)=0\) wakati\(x^2−2x=x(x−2)=0\). Kwa hiyo,\(x=0\) na\(x=2\) ni pointi muhimu. Kwa kuwa\(f\) haijulikani\(x=1\), tunahitaji kugawanya muda\((−∞,∞)\) katika vipindi vidogo\((−∞,0), (0,1), (1,2),\) na\((2,∞)\), na kuchagua hatua ya mtihani kutoka kila kipindi ili kutathmini ishara ya\(f′(x)\) kila moja ya vipindi hivi vidogo. Kwa mfano, hebu\(x=−1, x=\frac{1}{2}, x=\frac{3}{2}\), na\(x=3\) uwe pointi za mtihani kama inavyoonekana katika meza ifuatayo.
| Muda | Mtihani Point | Ishara ya\(f'(x)=\dfrac{x^2−2x}{(x−1)^2}\) | Hitimisho |
|---|---|---|---|
| \((−∞,0)\) | \(x=−1\) | \ (f' (x) =\ dfrac {x^2,12x} {(x-1) ^2}\)” data-valign="top"> (‡) (-) /+=+ | \(f\)inaongezeka. |
| \((0,1)\) | \(x=1/2\) | \ (f' (x) =\ dfrac {x^2,12x} {(x-1) ^2}\)” data-valign="top"> (+) (∙) /+=≈ | \(f\)inapungua. |
| \((1,2)\) | \(x=3/2\) | \ (f' (x) =\ dfrac {x^2,12x} {(x-1) ^2}\)” data-valign="top"> (+) (∙) /+=≈ | \(f\)inapungua. |
| \((2,∞)\) | \(x=3\) | \ (f' (x) =\ dfrac {x^2,12x} {(x-1) ^2}\)” data-valign="top"> (+) (+) /+=+ | \(f\)inaongezeka. |
Kutoka meza hii, tunaona kwamba\(f\) ina kiwango cha juu ndani katika\(x=0\) na kiwango cha chini ndani katika\(x=2\). Thamani ya\(f\) kiwango cha juu cha ndani ni\(f(0)=0\) na thamani ya\(f\) kiwango cha chini cha ndani ni\(f(2)=4\). Kwa hiyo,\((0,0)\) na\((2,4)\) ni pointi muhimu kwenye grafu.
Hatua ya 6. Tumia derivative ya pili:
\ [kuanza {align*} f "(x) &=\ frac {(x-1) ^2 (2x-1) ї2 (x-1) (x ^ 2,1x)} {(x,1-1) ^4}\\ [4pt]
&=\ frac {2 (x-1) ^2н (x^2,1x)]} {(x-1) ^4}\\ [4pt]
&=\ Frac {2 [x ^ 2-2x+1,1x^2x]} {(x-1) ^3}\\ [4pt]
&=\ Frac {2} {(x-1) ^3}. \ mwisho {align*}\]
Tunaona kwamba\(f''(x)\) ni kamwe sifuri au undefined kwa\(x\) katika uwanja wa\(f\). Kwa kuwa\(f\) haijulikani katika\(x=1\), kuangalia concavity sisi tu kugawanya muda\((−∞,∞)\) katika vipindi viwili vidogo\((−∞,1)\) na\((1,∞)\), na kuchagua mtihani uhakika kutoka kila kipindi kutathmini ishara ya\(f''(x)\) katika kila moja ya vipindi hivi. maadili\(x=0\) na\(x=2\) inawezekana pointi mtihani kama inavyoonekana katika meza ifuatayo.
| Muda | Mtihani Point | Ishara ya\(f''(x)=\dfrac{2}{(x−1)^3}\) | Hitimisho |
|---|---|---|---|
| \((−∞,1)\) | \(x=0\) | \ (f "(x) =\ dfrac {2} {(x-1) ^3}\)” style="text-align:katikati; ">\(+/−=−\) | \(f\)ni concave chini. |
| \((1,∞)\) | \(x=2\) | \ (f "(x) =\ dfrac {2} {(x-1) ^3}\)” style="text-align:katikati; ">\(+/+=+\) | \(f\)ni concave up |
Kutoka kwa habari zilizokusanywa, tunawasili kwenye grafu ifuatayo\(f.\)
Pata asymptote ya oblique kwa\(f(x)=\dfrac{3x^3−2x+1}{2x^2−4}\).
- Kidokezo
-
Tumia mgawanyiko mrefu wa polynomials.
- Jibu
-
\(y=\frac{3}{2}x\)
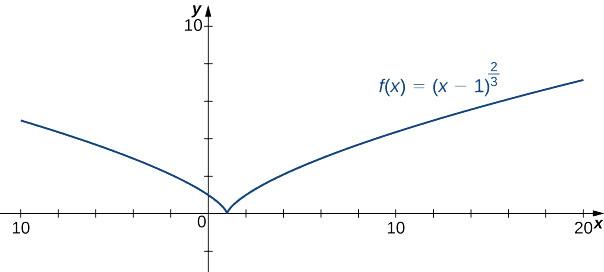
Mchoro grafu ya\(f(x)=(x−1)^{2/3}\)
Suluhisho
Hatua ya 1: Tangu kazi ya mizizi ya mchemraba hufafanuliwa kwa namba zote halisi\(x\) na\((x−1)^{2/3}=(\sqrt[3]{x−1})^2\), uwanja wa\(f\) ni namba zote halisi.
Hatua ya 2: Ili kupata\(y\) -intercept, tathmini\(f(0)\). Tangu\(f(0)=1,\)\(y\) -intercept ni\((0,1)\). Ili kupata\(x\) -intercept, tatua\((x−1)^{2/3}=0\). ufumbuzi wa equation hii ni\(x=1\), hivyo\(x\) -intercept ni\((1,0).\)
Hatua ya 3: Tangu\(\displaystyle \lim_{x→±∞}(x−1)^{2/3}=∞,\) kazi inaendelea kukua bila amefungwa kama\(x→∞\) na\(x→−∞.\)
Hatua ya 4: Kazi haina asymptotes wima.
Hatua ya 5: Kuamua wapi\(f\) ni kuongezeka au kupungua, mahesabu\(f′.\) Tunapata
\[f′(x)=\frac{2}{3}(x−1)^{−1/3}=\frac{2}{3(x−1)^{1/3}} \nonumber \]
Kazi hii si sifuri popote, lakini haijulikani wakati\(x=1.\) Kwa hiyo, hatua muhimu tu ni\(x=1.\) Gawanya muda\((−∞,∞)\) katika vipindi vidogo\((−∞,1)\) na\((1,∞)\), na kuchagua pointi mtihani katika kila moja ya vipindi hivi kuamua ishara ya\(f′(x)\) katika kila moja ya hizi vipindi vidogo. Hebu\(x=0\) na\(x=2\) uwe pointi za mtihani kama inavyoonekana katika meza ifuatayo.
| Muda | Mtihani Point | Ishara ya\(f′(x)=\frac{2}{3(x−1)^{1/3}}\) | Hitimisho |
|---|---|---|---|
| \((−∞,1)\) | \(x=0\) | \ (f′ (x) =\ frac {2} {3 (x-1) ^ {1/3}}\)” style="text-align:katikati; ">\(+/−=−\) | \(f\)inapungua |
| \((1,∞)\) | \(x=2\) | \ (f′ (x) =\ frac {2} {3 (x-1) ^ {1/3}}\)” style="text-align:katikati; ">\(+/+=+\) | \(f\)inaongezeka |
Tunahitimisha kwamba\(f\) ina kiwango cha chini ndani katika\(x=1\). Kutathmini\(f\) saa\(x=1\), tunaona kwamba thamani ya\(f\) kiwango cha chini cha ndani ni sifuri. Kumbuka kwamba\(f′(1)\) haijulikani, ili kuamua tabia ya kazi katika hatua hii muhimu, tunahitaji kuchunguza\(\displaystyle \lim_{x→1}f′(x).\) Kuangalia mipaka ya upande mmoja, tuna
\[\lim_{x→1^+}\frac{2}{3(x−1)^{1/3}}=∞\text{ and } \lim_{x→1^−}\frac{2}{3(x−1)^{1/3}}=−∞.\nonumber \]
Kwa hiyo,\(f\) ina cusp katika\(x=1.\)
Hatua ya 6: Kuamua concavity, sisi mahesabu derivative pili ya\(f:\)
\[f''(x)=−\dfrac{2}{9}(x−1)^{−4/3}=\dfrac{−2}{9(x−1)^{4/3}}. \nonumber \]
Tunaona kwamba\(f''(x)\) ni defined kwa ajili ya wote\(x\), lakini ni undefined wakati\(x=1\). Kwa hiyo, ugawanye muda\((−∞,∞)\) katika vipindi vidogo\((−∞,1)\) na\((1,∞)\), na uchague pointi za mtihani ili kutathmini ishara ya\(f''(x)\) kila moja ya vipindi hivi. Kama tulivyofanya mapema, basi\(x=0\) na\(x=2\) uwe na pointi za mtihani kama inavyoonekana katika meza ifuatayo.
| Muda | Mtihani Point | Ishara ya\(f''(x)=\dfrac{−2}{9(x−1)^{4/3}}\) | Hitimisho |
|---|---|---|---|
| \((−∞,1)\) | \(x=0\) | \ (f "(x) =\ dfrac {¯ 2} {9 (x-1) ^ {4/3}}\)” style="text-align:center; ">\(−/+=−\) | \(f\)ni concave chini |
| \((1,∞)\) | \(x=2\) | \ (f "(x) =\ dfrac {¯ 2} {9 (x-1) ^ {4/3}}\)” style="text-align:center; ">\(−/+=−\) | \(f\)ni concave chini |
Kutoka meza hii, tunahitimisha kwamba\(f\) ni concave chini kila mahali. Kuchanganya yote ya habari hii, sisi kufika katika graph zifuatazo kwa\(f\).
Fikiria kazi\(f(x)=5−x^{2/3}\). Tambua uhakika kwenye grafu ambapo cusp iko. Kuamua tabia ya mwisho ya\(f\).
- Kidokezo
-
kazi\(f\) ina cusp katika hatua\(a\) kama\(f(a)\) ipo,\(f'(a)\) ni undefined, moja ya mipaka upande mmoja kama\(x→a\) ya\(f'(x)\) ni\(+∞\), na nyingine upande mmoja kikomo ni\(−∞.\)
- Jibu
-
kazi\(f\) ina cusp katika\((0,5)\), tangu\(\displaystyle \lim_{x→0^−}f′(x)=∞\) na\(\displaystyle \lim_{x→0^+}f′(x)=−∞\). Kwa tabia ya mwisho,\(\displaystyle \lim_{x→±∞}f(x)=−∞.\)
Dhana muhimu
- Kikomo cha\(f(x)\) ni\(L\) kama\(x→∞\) (au\(x→−∞)\) kama maadili\(f(x)\) kuwa kiholela karibu na\(L\) kama\(x\) inakuwa kutosha kubwa.
- Kikomo cha\(f(x)\) ni\(∞\)\(x→∞\) kama\(f(x)\) inakuwa kikubwa kiholela kama\(x\) inakuwa kubwa ya kutosha. Kikomo cha\(f(x)\) ni\(−∞\)\(x→∞\) kama\(f(x)<0\) na\(|f(x)|\) inakuwa kiholela kikubwa kama\(x\) inakuwa kubwa ya kutosha. Tunaweza kufafanua kikomo cha\(x\) mbinu\(f(x)\) kama\(−∞\) vile vile.
- Kwa kazi ya polynomial\(p(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0,\) ambapo\(a_n≠0\), tabia ya mwisho imedhamiriwa na neno linaloongoza\(a_nx^n\). Ikiwa\(n≠0, p(x)\) mbinu\(∞\) au kila\(−∞\) mwisho.
- Kwa kazi ya busara tabia\(f(x)=\dfrac{p(x)}{q(x),}\) ya mwisho imedhamiriwa na uhusiano kati ya kiwango cha\(p\) na kiwango cha\(q\). Ikiwa kiwango cha\(p\) ni chini ya kiwango cha\(q\), mstari\(y=0\) ni asymptote ya usawa kwa\(f\). Ikiwa kiwango cha\(p\) ni sawa na kiwango cha\(q\), basi mstari\(y=\dfrac{a_n}{b_n}\) ni asymptote ya usawa, wapi\(a_n\) na\(b_n\) ni coefficients inayoongoza ya\(p\) na\(q\), kwa mtiririko huo. Kama kiwango cha\(p\) ni kubwa kuliko kiwango cha\(q\), basi\(f\) mbinu\(∞\) au\(−∞\) katika kila mwisho.
faharasa
- tabia ya mwisho
- tabia ya kazi kama\(x→∞\) na\(x→−∞\)
- asymptote ya usawa
- ikiwa\(\displaystyle \lim_{x→∞}f(x)=L\) au\(\displaystyle \lim_{x→−∞}f(x)=L\), basi\(y=L\) ni dalili ya usawa ya\(f\)
- kikomo usio na mwisho
- kazi ambayo inakuwa kiholela kubwa kama\(x\) inakuwa kubwa
- kikomo katika infinity
- kazi ambayo inakaribia thamani kikomo\(L\) kama\(x\) inakuwa kubwa
- dalili ya oblique
- mstari\(y=mx+b\) ikiwa\(f(x)\) unakaribia kama\(x→∞\) au\( x→−∞\)


