4.5: Derivatives na Shape ya Grafu

Last updated
Save as PDF

Page ID: 178846

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Eleza jinsi ishara ya derivative ya kwanza huathiri sura ya grafu ya kazi.
Weka mtihani wa kwanza wa derivative kwa pointi muhimu.
Tumia pointi za concavity na kufuta ili kuelezea jinsi ishara ya derivative ya pili inathiri sura ya grafu ya kazi.
Eleza mtihani wa concavity kwa kazi juu ya muda wazi.
Eleza uhusiano kati ya kazi na derivatives yake ya kwanza na ya pili.
Hali ya pili derivative mtihani kwa extrema mitaa.

Mapema katika sura hii sisi alisema kwamba kama kazi\(f\) ina extremum ndani katika hatua\(c\), basi\(c\) lazima hatua muhimu ya\(f\). Hata hivyo, kazi haihakikishiwa kuwa na extremum ya ndani katika hatua muhimu. Kwa mfano,\(f(x)=x^3\) ina hatua muhimu katika\(x=0\) tangu\(f'(x)=3x^2\) ni sifuri katika\(x=0\), lakini\(f\) hana extremum ndani katika\(x=0\). Kutumia matokeo kutoka sehemu ya awali, sasa tuna uwezo wa kuamua kama hatua muhimu ya kazi kweli inalingana na thamani ya ndani uliokithiri. Katika sehemu hii, sisi pia kuona jinsi derivative pili hutoa taarifa kuhusu sura ya grafu kwa kuelezea kama graph ya kazi curves zaidi au curves kushuka.

Jaribio la kwanza la derivative

Corollary\(3\) ya Theorem ya Thamani ya Maana ilionyesha kwamba ikiwa derivative ya kazi ni chanya zaidi ya muda\(I\) basi kazi inaongezeka zaidi\(I\). Kwa upande mwingine, ikiwa derivative ya kazi ni hasi juu ya muda\(I\), basi kazi inapungua juu\(I\) kama inavyoonekana katika takwimu zifuatazo.

Takwimu hii ni kuvunjwa katika takwimu nne kinachoitwa a, b, c, na d. takwimu inaonyesha kazi kuongezeka convexly kutoka (a, f (a)) kwa (b, f (b)). Katika pointi mbili derivative ni kuchukuliwa na ni alibainisha kuwa katika wote f' — Kielelezo\(\PageIndex{1}\): Kazi zote mbili zinaongezeka zaidi ya muda\((a,b)\). Katika kila hatua\(x\), derivative\(f'(x)>0\). Kazi zote mbili zinapungua kwa muda\((a,b)\). Katika kila hatua\(x\), derivative\(f'(x)<0.\)

Kazi inayoendelea\(f\) ina upeo wa ndani kwa uhakika\(c\) ikiwa na tu ikiwa\(f\) inachukua kuongezeka hadi kupungua kwa hatua\(c\). Vile vile,\(f\) ina kiwango cha chini cha ndani\(c\) ikiwa na tu kama\(f\) swichi kutoka kupungua kwa kuongezeka kwa\(c\). Kama\(f\) ni kazi ya kuendelea juu ya muda\(I\) zenye\(c\) na kutofautisha juu ya\(I\), ila uwezekano katika\(c\), njia pekee\(f\) inaweza kubadili kutoka kuongezeka kwa kupungua (au kinyume chake) katika hatua\(c\) ni kama\(f'\) mabadiliko ishara kama \(x\)kuongezeka kwa njia ya\(c\). Kama\(f\) ni differentiable katika\(c\), njia pekee ambayo\(f'\) inaweza kubadilisha ishara kama\(x\) kuongezeka kwa njia\(c\) ya ni kama\(f'(c)=0\). Kwa hiyo, kwa ajili ya kazi\(f\) ambayo ni kuendelea juu ya muda\(I\) zenye\(c\) na kutofautisha juu ya\(I\), ila uwezekano katika\(c\), njia pekee\(f\) inaweza kubadili kutoka kuongezeka kwa kupungua (au kinyume chake) ni kama\(f'(c)=0\) au\(f'(c)\) haijulikani. Kwa hiyo, ili kupata extrema ya ndani kwa kazi\(f\), tunatafuta pointi\(c\) katika uwanja wa\(f\) vile\(f'(c)=0\) au\(f'(c)\) haijulikani. Kumbuka kwamba pointi hizo zinaitwa pointi muhimu ya\(f\).

Kumbuka kwamba\(f\) haja ya kuwa na extrema ya ndani katika hatua muhimu. pointi muhimu ni wagombea kwa extrema mitaa tu. Katika Kielelezo\(\PageIndex{2}\), tunaonyesha kwamba ikiwa kazi inayoendelea\(f\) ina extremum ya ndani, inapaswa kutokea kwa hatua muhimu, lakini kazi inaweza kuwa na extremum ya ndani katika hatua muhimu. Tunaonyesha kwamba ikiwa\(f\) ina extremum ya ndani katika hatua muhimu, basi ishara ya\(f'\) swichi\(x\) inakua kupitia hatua hiyo.

Kazi f (x) imewekwa. Inaanza katika roboduara ya pili na huongezeka hadi x = a, ambayo ni kali mno na hivyo f' (a) haijulikani. Katika sehemu hii f' — Kielelezo\(\PageIndex{2}\): Kazi\(f\) ina pointi nne muhimu:\(a,b,c\), na\(d\). kazi\(f\) ina maxima ndani katika\(a\) na\(d\), na kiwango cha chini ndani katika\(b\). Kazi\(f\) haina extremum ndani ya saa\(c\). Ishara ya\(f'\) mabadiliko katika extrema zote za mitaa.

Kutumia Kielelezo\(\PageIndex{2}\), sisi muhtasari matokeo makuu kuhusu extrema ya ndani.

Ikiwa kazi inayoendelea\(f\) ina extremum ya ndani, inapaswa kutokea kwa hatua muhimu\(c\).
Kazi ina extremum mitaa katika hatua muhimu\(c\) kama na tu kama\(f'\) swichi derivative ishara kama\(x\) kuongezeka kwa njia ya\(c\).
Kwa hiyo, ili kupima kama kazi ina extremum ya ndani katika hatua muhimu\(c\), ni lazima kuamua ishara ya\(f'(x)\) kushoto na kulia ya\(c\).

Matokeo haya inajulikana kama mtihani wa kwanza wa derivative.

kwanza derivative mtihani

Tuseme kwamba\(f\) ni kazi inayoendelea juu ya muda\(I\) iliyo na hatua muhimu\(c\). Ikiwa\(f\) ni tofauti zaidi\(I\), isipokuwa labda kwa uhakika\(c\), kisha\(f(c)\) hutimiza mojawapo ya maelezo yafuatayo:

Kama\(f'\) mabadiliko ishara kutoka chanya wakati\(x<c\) hasi wakati\(x>c\), basi\(f(c)\) ni upeo wa ndani wa\(f\).
Kama\(f'\) mabadiliko ishara kutoka hasi wakati\(x<c\) chanya wakati\(x>c\), basi\(f(c)\) ni chini ya ndani ya\(f\).
Kama\(f'\) ina ishara hiyo kwa\(x<c\) na\(x>c\), basi\(f(c)\) si upeo wa ndani wala chini ya ndani ya\(f\)

Sasa hebu tuangalie jinsi ya kutumia mkakati huu ili kupata extrema zote za mitaa kwa kazi fulani.

Mfano\(\PageIndex{1}\): Using the First Derivative Test to Find Local Extrema

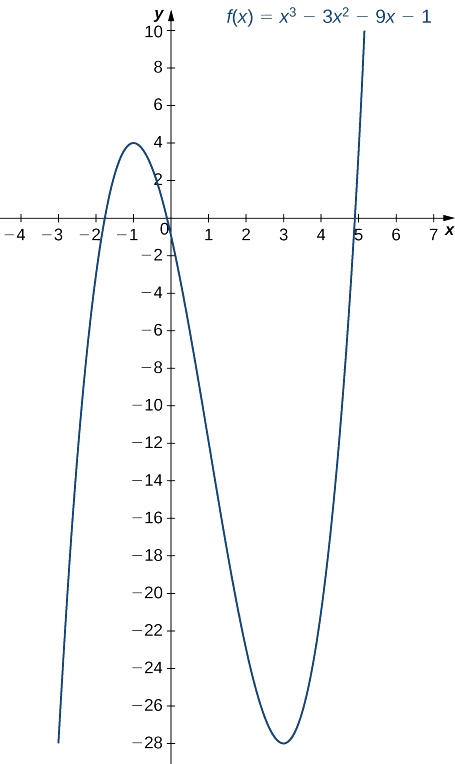
Tumia mtihani wa kwanza wa derivative ili kupata eneo la extrema zote za mitaa kwa\(f(x)=x^3−3x^2−9x−1.\) Matumizi ya matumizi ya graphing ili kuthibitisha matokeo yako.

Suluhisho

Hatua ya 1. Derivative ni\(f'(x)=3x^2−6x−9.\) Ili kupata pointi muhimu, tunahitaji kupata wapi kuzingatia\(f'(x)=0.\) polynomial, tunahitimisha kuwa pointi muhimu zinapaswa kukidhi

\[3(x^2−2x−3)=3(x−3)(x+1)=0. \nonumber \]

Kwa hiyo, pointi muhimu ni\(x=3,−1.\) Sasa kugawanya muda\((−∞,∞)\) katika vipindi vidogo\((−∞,−1),(−1,3)\) na\((3,∞).\)

Hatua ya 2. Kwa kuwa\(f'\) ni kazi inayoendelea, kuamua ishara ya\(f'(x)\) juu ya kila subinterval, inatosha kuchagua uhakika juu ya kila vipindi\((−∞,−1),(−1,3)\)\((3,∞)\) na kuamua ishara ya kila\(f'\) moja ya pointi hizi. Kwa mfano, hebu tuchague\(x=−2\)\(x=0\), na\(x=4\) kama pointi za mtihani.

Jedwali\(\PageIndex{1}\): Mtihani wa kwanza wa derivative\(f(x)=x^3−3x^2−9x−1.\)
Muda	Mtihani Point	Ishara ya\(f'(x)=3(x−3)(x+1)\) katika Point ya Mtihani	Hitimisho
\((−∞,−1)\)	\(x=−2\)	\ (f' (x) =3 (x-1) (x+1)\) katika Kiwango cha Mtihani” style="wima align:katikati; "> (+) (-) (-) =+	\(f\)inaongezeka.
\((−1,3)\)	\(x=0\)	\ (f' (x) =3 (x-1) (x+1)\) katika Kiwango cha Mtihani” style="wima align:katikati; "> (+) (∙) (+) =-	\(f\)inapungua.
\((3,∞)\)	\(x=4\)	\ (f' (x) =3 (x-1) (x+1)\) katika Kiwango cha Mtihani” style="wima align:katikati; "> (+) (+) (+) =+	\(f\)inaongezeka.

Hatua ya 3. Tangu\(f'\) swichi ishara kutoka chanya kwa hasi kama\(x\) kuongezeka kwa njia ya\(-1\),\(f\) ina kiwango cha juu ndani katika\(x=−1\). Tangu\(f'\) swichi ishara kutoka hasi kwa chanya kama\(x\) kuongezeka kwa njia ya\(3\),\(f\) ina kiwango cha chini ndani katika\(x=3\). Matokeo haya ya uchambuzi yanakubaliana na grafu ifuatayo.

Kazi f (x) = x3 - 3x2 - 9x - 1 ni graphed. Ina kiwango cha juu katika x = -1 na kiwango cha chini katika x = 3. Kazi inaongezeka kabla ya x = -1, kupungua hadi x = 3, na kisha kuongezeka baada ya hayo. — Kielelezo\(\PageIndex{3}\): Kazi\(f\) ina kiwango cha juu\(x=−1\) na kiwango cha chini\(x=3\)

Zoezi\(\PageIndex{1}\)

Matumizi ya kwanza derivative mtihani Machapisho extrema zote za mitaa kwa\(f(x)=−x^3+\frac{3}{2}x^2+18x.\)

Kidokezo: Kupata pointi zote muhimu ya\(f\) na kuamua ishara ya\(f'(x)\) zaidi ya vipindi fulani kuamua na pointi muhimu.

Jibu: \(f\)ina kiwango cha chini ndani katika\(−2\) na kiwango cha juu ndani katika\(3\).

Mfano\(\PageIndex{2}\): Using the First Derivative Test

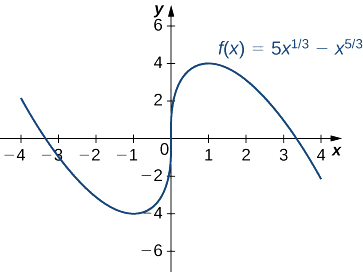
Tumia mtihani wa kwanza wa derivative ili kupata eneo la extrema zote za mitaa kwa\(f(x)=5x^{1/3}−x^{5/3}.\) Matumizi ya matumizi ya graphing ili kuthibitisha matokeo yako.

Suluhisho

Hatua ya 1. Derivative ni

\[f'(x)=\frac{5}{3}x^{−2/3}−\frac{5}{3}x^{2/3}=\frac{5}{3x^{2/3}}−\frac{5x^{2/3}}{3}=\frac{5−5x^{4/3}}{3x^{2/3}}=\frac{5(1−x^{4/3})}{3x^{2/3}}.\nonumber \]

derivative\(f'(x)=0\) wakati\(1−x^{4/3}=0.\) Kwa hiyo,\(f'(x)=0\) katika\(x=±1\). derivative\(f'(x)\) ni undefined katika\(x=0.\) Kwa hiyo, tuna pointi tatu muhimu:\(x=0\)\(x=1\),, na\(x=−1\). Kwa hiyo, ugawanye muda\((−∞,∞)\) katika vipindi vidogo\((−∞,−1),\,(−1,0),\,(0,1)\), na\((1,∞)\).

Hatua ya 2: Kwa kuwa\(f'\) ni kuendelea juu ya kila subinterval, inatosha kuchagua hatua ya mtihani\(x\) katika kila moja ya vipindi kutoka hatua ya 1 na kuamua ishara ya\(f'\) katika kila moja ya pointi hizi. pointi\(x=−2,\,x=−\frac{1}{2},\,x=\frac{1}{2}\), na\(x=2\) ni pointi mtihani kwa vipindi hivi.

Jedwali\(\PageIndex{2}\): Mtihani wa kwanza wa derivative\(f(x)=5x^{1/3}−x^{5/3}.\)
Muda	Mtihani Point	Ishara ya\(f'(x)=\frac{5(1−x^{4/3})}{3x^{2/3}}\) katika Point ya Mtihani	Hitimisho
\((−∞,−1)\)	\(x=−2\)	\ (f' (x) =\ frac {5 (1,1x^ {4/3})} {3x^ {2/3}}\) katika Kiwango cha Mtihani” style="wima align:katikati; ">\(\frac{(+)(−)}{+}=−\)	\(f\)inapungua.
\((−1,0)\)	\(x=−\frac{1}{2}\)	\ (f' (x) =\ frac {5 (1,1x^ {4/3})} {3x^ {2/3}}\) katika Kiwango cha Mtihani” style="wima align:katikati; ">\(\frac{(+)(+)}{+}=+\)	\(f\)inaongezeka.
\((0,1)\)	\(x=\frac{1}{2}\)	\ (f' (x) =\ frac {5 (1,1x^ {4/3})} {3x^ {2/3}}\) katika Kiwango cha Mtihani” style="wima align:katikati; ">\(\frac{(+)(+)}{+}=+\)	\(f\)inaongezeka.
\((1,∞)\)	\(x=2\)	\ (f' (x) =\ frac {5 (1,1x^ {4/3})} {3x^ {2/3}}\) katika Kiwango cha Mtihani” style="wima align:katikati; ">\(\frac{(+)(−)}{+}=−\)	\(f\)inapungua.

Hatua ya 3: Kwa kuwa\(f\) ni kupungua zaidi ya muda\((−∞,−1)\) na kuongeza zaidi ya muda\((−1,0)\),\(f\) ina kiwango cha chini ndani katika\(x=−1\). Kwa kuwa\(f\) ni kuongezeka zaidi ya muda\((−1,0)\) na muda\((0,1)\),\(f\) hana extremum ndani saa\(x=0\). Kwa kuwa\(f\) ni kuongezeka zaidi ya muda\((0,1)\) na kupungua zaidi ya muda\((1,∞)\),\(f\) ina kiwango cha juu ndani katika\(x=1\). Matokeo ya uchambuzi yanakubaliana na grafu ifuatayo.

Kazi f (x) = 5x1/3 - x5/3 imewekwa. Inapungua hadi kiwango cha chini chake cha ndani kwa x = -1, huongezeka hadi x = 1, halafu hupungua baada ya hapo. — Kielelezo\(\PageIndex{4}\): kazi\(f\) ina kiwango cha chini ndani katika\(x=−1\) na upeo wa ndani katika\(x=1\)

Zoezi\(\PageIndex{2}\)

Matumizi ya kwanza derivative mtihani kupata extrema zote za mitaa kwa\(f(x)=\dfrac{3}{x−1}\).

Kidokezo: tu muhimu hatua ya\(f\) ni\(x=1.\)

Jibu: \(f\)hana extrema ndani kwa sababu\(f'\) haina mabadiliko ya ishara katika\(x=1\).

Concavity na Pointi ya Inflection

Sasa tunajua jinsi ya kuamua ambapo kazi inaongezeka au kupungua. Hata hivyo, kuna suala jingine la kuzingatia kuhusu sura ya grafu ya kazi. Kama curves graph, je, ni Curve zaidi au Curve kushuka? Dhana hii inaitwa concavity ya kazi.

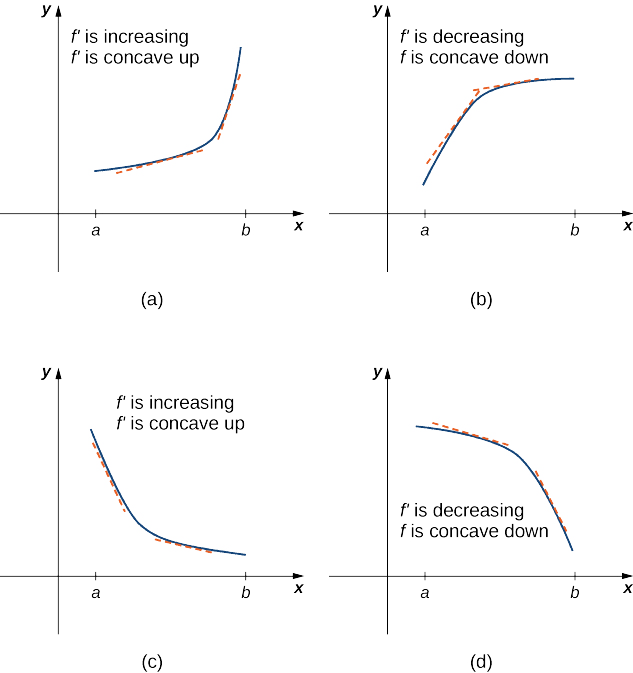
Kielelezo\(\PageIndex{5a}\) inaonyesha kazi\(f\) na grafu kwamba curves zaidi. Kama\(x\) inavyoongezeka, mteremko wa mstari wa tangent huongezeka. Hivyo, tangu derivative\(x\) kuongezeka kama ongezeko,\(f'\) ni kazi kuongezeka. Tunasema kazi hii\(f\) ni concave up. Kielelezo\(\PageIndex{5b}\) inaonyesha kazi\(f\) kwamba curves kushuka. Kama\(x\) inavyoongezeka, mteremko wa mstari wa tangent hupungua. Tangu derivative itapungua kama\(x\) ongezeko,\(f'\) ni kazi kupungua. Tunasema kazi hii\(f\) ni concave chini.

Ufafanuzi: mtihani wa concavity

Hebu\(f\) iwe kazi ambayo inatofautiana juu ya muda wa wazi\(I\). Kama\(f'\) ni kuongeza juu ya\(I\), tunasema\(f\) ni concave juu ya\(I\). Kama\(f'\) ni kupungua juu ya\(I\), tunasema\(f\) ni concave chini juu ya\(I\).

Takwimu hii ni kuvunjwa katika takwimu nne kinachoitwa a, b, c, na d. takwimu inaonyesha kazi kuongezeka convexly kutoka (a, f (a)) kwa (b, f (b)). Kwa pointi mbili derivative inachukuliwa na wote wanaongezeka, lakini moja kuchukuliwa zaidi kwa haki inaongezeka zaidi. Ni alibainisha kuwa f' ni kuongezeka na f ni concave up. Kielelezo b kinaonyesha kazi inayoongezeka kwa concavely kutoka (a, f (a)) hadi (b, f (b)). Kwa pointi mbili derivative inachukuliwa na wote wanaongezeka, lakini moja kuchukuliwa zaidi kwa haki inaongezeka kidogo. Ni alibainisha kuwa f' ni kupungua na f ni concave chini. Kielelezo c inaonyesha kazi kupungua kwa concavely kutoka (a, f (a)) hadi (b, f (b)). Kwa pointi mbili derivative inachukuliwa na wote wawili hupungua, lakini moja kuchukuliwa zaidi kwa haki ni kupungua chini. Ni alibainisha kuwa f' ni kuongezeka na f ni concave up. Kielelezo d inaonyesha kazi kupungua kwa convexly kutoka (a, f (a)) hadi (b, f (b)). Kwa pointi mbili derivative inachukuliwa na wote wawili hupungua, lakini moja kuchukuliwa zaidi kwa haki ni kupungua zaidi. Ni alibainisha kuwa f' ni kupungua na f ni concave chini. — Kielelezo\(\PageIndex{5}\): (a), (c) Kwa kuwa\(f'\) ni kuongeza zaidi ya muda\((a,b)\), tunasema\(f\) ni concave up juu\((a,b). (b), (d)\) Tangu\(f'\) ni kupungua zaidi ya muda\((a,b)\), tunasema\(f\) ni concave chini juu\((a,b).\)

Kwa ujumla, bila kuwa na grafu ya kazi\(f\), tunawezaje kuamua concavity yake? Kwa ufafanuzi, kazi\(f\) ni concave up kama\(f'\) ni kuongezeka. Kutoka Corollary\(3\), tunajua kwamba ikiwa\(f'\) ni kazi tofauti, basi\(f'\) inaongezeka kama derivative yake\(f''(x)>0\). Kwa hiyo, kazi\(f\) ambayo ni mara mbili kutofautisha ni concave up wakati\(f''(x)>0\). Vile vile, kazi\(f\) ni concave chini ikiwa\(f'\) inapungua. Tunajua kwamba kazi tofauti\(f'\) ni kupungua kama derivative yake\(f''(x)<0\). Kwa hiyo, kazi ya kutofautisha mara\(f\) mbili-ni concave chini wakati\(f''(x)<0\). Kutumia mantiki hii inajulikana kama mtihani wa concavity.

Mtihani wa Concavity

Hebu\(f\) kuwa kazi ambayo ni mara mbili kutofautisha zaidi ya muda\(I\).

Ikiwa\(f''(x)>0\) kwa wote\(x∈I\), basi\(f\) ni concave juu\(I\)
Kama\(f''(x)<0\) kwa ajili ya wote\(x∈I,\) basi\(f\) ni concave chini juu ya\(I\).

Tunahitimisha kwamba tunaweza kuamua concavity ya kazi\(f\) kwa kuangalia derivative pili ya\(f\). Kwa kuongeza, tunaona kwamba kazi\(f\) inaweza kubadili concavity (Kielelezo\(\PageIndex{6}\)). Hata hivyo, kazi inayoendelea inaweza kubadili concavity tu kwa hatua\(x\) ikiwa\(f''(x)=0\) au\(f''(x)\) haijulikani. Kwa hiyo, kuamua vipindi ambapo kazi\(f\) ni concave juu na concave chini, tunatafuta maadili hayo ya\(x\) wapi\(f''(x)=0\) au\(f''(x)\) haijulikani. Tunapoamua pointi hizi, tunagawanya uwanja wa\(f\) ndani ya vipindi vidogo na kuamua ishara ya\(f''\) juu ya kila moja ya vipindi hivi vidogo. Ikiwa\(f''\) mabadiliko yanaashiria tunapopitia hatua\(x\), basi\(f\) mabadiliko ya concavity. Ni muhimu kukumbuka kuwa kazi\(f\) haiwezi kubadilisha concavity kwa uhakika\(x\) hata kama\(f''(x)=0\) au\(f''(x)\) haijulikani. Kama, hata hivyo,\(f\) haina mabadiliko concavity katika hatua\(a\) na\(f\) ni kuendelea katika\(a\), tunasema uhakika\((a,f(a))\) ni hatua inflection ya\(f\).

Ufafanuzi: hatua ya kupindua

Kama\(f\) ni kuendelea katika\(a\) na\(f\) mabadiliko concavity katika\(a\), uhakika\((a, \,f(a))\) ni hatua inflection ya\(f\).

Kazi ya sinusoidal inavyoonyeshwa kuwa imebadilishwa kwenye quadrant ya kwanza. Kazi huanza kupungua, hivyo f' < 0 and f” — Kielelezo\(\PageIndex{6}\): Tangu\(f''(x)>0\) kwa\(x<a\), kazi\(f\) ni concave juu ya muda\((−∞,a)\). Tangu\(f''(x)<0\) kwa\(x>a\), kazi\(f\) ni concave chini juu ya muda\((a,∞)\). Hatua\((a,f(a))\) ni hatua ya kupigia\(f\).

Mfano\(\PageIndex{3}\): Testing for Concavity

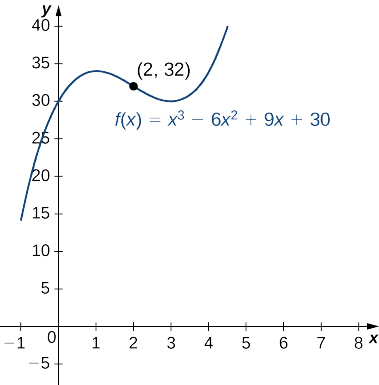
Kwa kazi\(f(x)=x^3−6x^2+9x+30,\) kuamua vipindi vyote ambapo\(f\) ni concave juu na vipindi vyote ambapo\(f\) ni concave chini. Orodha ya pointi zote za kupindua\(f\). Tumia matumizi ya graphing ili kuthibitisha matokeo yako.

Suluhisho

Kuamua concavity, tunahitaji kupata derivative ya pili\(f''(x).\) derivative ya kwanza ni\(f'(x)=3x^2−12x+9,\) hivyo derivative ya pili ni\(f''(x)=6x−12.\) Kama kazi inabadilika concavity, hutokea ama wakati\(f''(x)=0\) au\(f''(x)\) haijulikani. Tangu\(f''\) hufafanuliwa kwa namba zote halisi\(x\), tunahitaji tu kupata wapi\(f''(x)=0\). Kutatua equation\(6x−12=0\), tunaona kwamba\(x=2\) ni mahali pekee ambapo\(f\) inaweza kubadilisha concavity. Sisi sasa mtihani pointi juu ya vipindi\((−∞,2)\) na\((2,∞)\) kuamua concavity ya\(f\). Pointi\(x=0\) na\(x=3\) ni pointi za mtihani kwa vipindi hivi.

Jedwali:\(\PageIndex{3}\): Mtihani wa Concavity kwa\(f(x)=x^3−6x^2+9x+30.\)
Muda	Mtihani Point	Ishara ya\(f''(x)=6x−12\) katika Point ya Mtihani	Hitimisho
\((−∞,2)\)	\(x=0\)	\ (f "(x) =6x-12\) katika Kiwango cha Mtihani” style="wima align:middle; ">	\(f\)ni concave chini
\((2,∞)\)	\(x=3\)	\ (f "(x) =6x-12\) katika Kiwango cha Mtihani” style="wima align:middle; ">+	\(f\)ni concave up

Tunahitimisha kuwa\(f\) ni concave chini juu ya muda\((−∞,2)\) na concave juu ya muda\((2,∞)\). Kwa kuwa\(f\) mabadiliko ya concavity saa\(x=2\), hatua\((2,f(2))=(2,32)\) ni hatua ya kufuta. Kielelezo\(\PageIndex{7}\) kinathibitisha matokeo ya uchambuzi.

Kazi f (x) = x3 - 6x2 + 9x + 30 imewekwa. Hatua ya kupigia (2, 32) imewekwa alama, na ni takribani equidistant kutoka extrema mbili za ndani. — Kielelezo\(\PageIndex{7}\): Kazi iliyotolewa ina hatua ya kufuta\((2,32)\) ambapo grafu inabadilika concavity.

Zoezi\(\PageIndex{3}\)

Kwa\(f(x)=−x^3+\frac{3}{2}x^2+18x\), kupata vipindi vyote ambapo\(f\) ni concave juu na vipindi vyote ambapo\(f\) ni concave chini.

Kidokezo: Pata wapi\(f''(x)=0\)

Jibu: \(f\)ni concave juu ya muda\((−∞,\frac{1}{2})\) na concave chini juu ya muda\((\frac{1}{2},∞)\)

Sasa muhtasari, katika Jedwali\(\PageIndex{4}\), taarifa kwamba derivatives kwanza na ya pili ya kazi\(f\) kutoa kuhusu grafu ya\(f\), na kuonyesha taarifa hii katika Kielelezo\(\PageIndex{8}\).

Jedwali:\(\PageIndex{4}\): Nini derivatives Tuambie kuhusu Grafu
Ishara ya\(f'\)	Ishara ya\(f''\)	Ni\(f\) kuongezeka au kupungua?	Concavity
\ (f'\)” style="wima align:middle; "> Chanya	\ (f "\)” style="wima align:middle; "> Chanya	\ (f\) kuongezeka au kupungua?” style="vertical-align:middle; "> Kuongezeka	Concave up
\ (f'\)” style="wima align:middle; "> Chanya	\ (f "\)” style="wima align:middle; "> Hasi	\ (f\) kuongezeka au kupungua?” style="vertical-align:middle; "> Kuongezeka	Concave chini
\ (f'\)” style="wima align:middle; "> Hasi	\ (f "\)” style="wima align:middle; "> Chanya	\ (f\) kuongezeka au kupungua?” style="wima align:middle; "> Kupungua	Concave up
\ (f'\)” style="wima align:middle; "> Hasi	\ (f "\)” style="wima align:middle; "> Hasi	\ (f\) kuongezeka au kupungua?” style="wima align:middle; "> Kupungua	Concave chini

Kazi imewekwa katika roboduara ya kwanza. Imevunjika katika sehemu nne, na mapumziko yanayotokana na kiwango cha chini cha ndani, kiwango cha juu, na upeo wa ndani, kwa mtiririko huo. Sehemu ya kwanza ni kupungua na concave up; hapa, f' < 0 and f” — Takwimu: Fikiria kazi\(\PageIndex{8}\) ya kutofautisha mara mbili-juu\(f\) ya muda wa wazi.\(I\) Ikiwa\(f'(x)>0\) kwa wote\(x∈I\), kazi inaongezeka\(I\). Ikiwa\(f'(x)<0\) kwa wote\(x∈I\), kazi inapungua\(I\). Kama\(f''(x)>0\) kwa ajili ya wote\(x∈I\), kazi ni concave up. Kama\(f''(x)<0\) kwa ajili ya wote\(x∈I\), kazi ni concave chini ya\(I\).

Jaribio la pili la derivative

Mtihani wa kwanza wa derivative hutoa chombo cha uchambuzi cha kutafuta extrema ya ndani, lakini derivative ya pili pia inaweza kutumika kupata maadili uliokithiri. Kutumia derivative ya pili wakati mwingine inaweza kuwa njia rahisi kuliko kutumia derivative ya kwanza.

Tunajua kwamba ikiwa kazi inayoendelea ina extremum ya ndani, inapaswa kutokea kwa hatua muhimu. Hata hivyo, kazi haina haja ya kuwa na extremum ya ndani katika hatua muhimu. Hapa tunachunguza jinsi mtihani wa pili wa derivative unaweza kutumika kuamua kama kazi ina extremum ya ndani katika hatua muhimu. Hebu\(f\) kuwa kazi ya kutofautisha mara mbili-kama hiyo\(f'(a)=0\) na\(f''\) inaendelea juu ya muda wazi\(I\) iliyo na\(a\). Tuseme\(f''(a)<0\). Tangu\(f''\) ni kuendelea juu\(I, f''(x)<0\) kwa ajili ya wote\(x∈I\) (Kielelezo\(\PageIndex{9}\)). Kisha, na Corollary\(3\),\(f'\) ni kazi kupungua juu ya\(I\). Tangu\(f'(a)=0\), tunahitimisha kwamba kwa wote\(x∈I, \,f'(x)>0\)\(f'(x)<0\) ikiwa\(x<a\) na kama\(x>a\). Kwa hiyo, kwa mtihani wa kwanza wa derivative,\(f\) ina upeo wa ndani\(x=a\).

Kwa upande mwingine, tuseme kuna uhakika\(b\) kama kwamba\(f'(b)=0\) lakini\(f''(b)>0\). Tangu\(f''\) ni kuendelea juu ya muda wazi\(I\) zenye\(b\), basi\(f''(x)>0\) kwa wote\(x∈I\) (Kielelezo\(\PageIndex{9}\)). Kisha, na Corollary\(3\),\(f'\) ni kazi kuongezeka juu ya\(I\). Tangu\(f'(b)=0\), tunahitimisha kuwa kwa wote\(x∈I\),\(f'(x)<0\) ikiwa\(x<b\) na\(f'(x)>0\) ikiwa\(x>b\). Kwa hiyo, kwa mtihani wa kwanza wa derivative,\(f\) ina kiwango cha chini cha ndani\(x=b.\)

kazi f (x) ni graphed katika roboduara ya kwanza na b alama kwenye x-axis. Kazi ni wazi sinusoidal, kuongezeka kwanza kwa x = a, kisha kupungua kwa x = b, na kuongezeka tena. Katika (a, f (a)), tangent ni alama, na ni alibainisha kuwa f' (a) = 0 na f” (a) <0. Katika (b, f (b)), tangent ni alama, na inajulikana f' (b) = 0 na f” (b) — Kielelezo\(\PageIndex{9}\): Fikiria kazi ya kutofautisha mara\(f\) mbili-kama hiyo\(f''\) inaendelea. Tangu\(f'(a)=0\) na\(f''(a)<0\), kuna muda\(I\) zenye\(a\) vile kwamba kwa wote\(x\) katika\(I\),\(f\) ni kuongezeka kama\(x<a\) na\(f\) ni kupungua kama\(x>a\). Matokeo yake,\(f\) ina upeo wa ndani katika\(x=a\). Tangu\(f'(b)=0\) na\(f''(b)>0\), kuna muda\(I\) zenye\(b\) vile kwamba kwa wote\(x\) katika\(I\),\(f\) ni kupungua kama\(x<b\) na\(f\) ni kuongezeka kama\(x>b\). Matokeo yake,\(f\) ina kiwango cha chini ndani katika\(x=b\).

pili derivative mtihani

Tuseme\(f'(c)=0\) na\(f''\) ni kuendelea juu ya muda zenye\(c\).

Ikiwa\(f''(c)>0\), basi\(f\) ina kiwango cha chini cha ndani\(c\).
Ikiwa\(f''(c)<0\), basi\(f\) ina kiwango cha juu cha ndani\(c\).
Ikiwa\(f''(c)=0,\) basi mtihani haujulikani.

Kumbuka kwamba kwa kesi ii. wakati\(f''(c)=0\), basi\(f\) inaweza kuwa na upeo wa ndani, chini ya ndani, au wala katika\(c\). Kwa mfano, kazi\(f(x)=x^3, \; f(x)=x^4,\) na\(f(x)=−x^4\) wote wana pointi muhimu katika\(x=0\). Katika kila kesi, derivative ya pili ni sifuri saa\(x=0\). Hata hivyo, kazi\(f(x)=x^4\) ina kiwango cha chini cha ndani wakati\(x=0\) ambapo kazi\(f(x)=−x^4\) ina kiwango cha juu cha ndani\(x=0\), na kazi\(f(x)=x^3\) haina extremum ya ndani\(x=0\).

Hebu sasa tuangalie jinsi ya kutumia mtihani wa pili wa derivative ili kuamua ikiwa\(f\) ina kiwango cha juu cha ndani au cha chini cha ndani katika hatua muhimu\(c\) ambapo\(f'(c)=0.\)

Mfano\(\PageIndex{4}\): Using the Second Derivative Test

Tumia derivative pili ili kupata eneo la extrema zote za mitaa\(f(x)=x^5−5x^3.\)

Suluhisho

Ili kutumia mtihani wa pili wa derivative, sisi kwanza tunahitaji kupata pointi muhimu\(c\) ambapo\(f'(c)=0\). Derivative ni\(f'(x)=5x^4−15x^2\). Kwa hiyo,\(f'(x)=5x^4−15x^2=5x^2(x^2−3)=0\) wakati\(x=0,\,±\sqrt{3}\).

Kuamua kama\(f\) ina extremum ya ndani katika yoyote ya pointi hizi, tunahitaji kutathmini ishara ya\(f''\) pointi hizi. Derivative ya pili ni

\(f''(x)=20x^3−30x=10x(2x^2−3).\)

Katika meza ifuatayo, tunatathmini derivative ya pili katika kila moja ya pointi muhimu na kutumia mtihani wa pili wa derivative ili kuamua ikiwa\(f\) ina kiwango cha juu cha ndani au cha chini cha ndani wakati wowote wa pointi hizi.

Jedwali\(\PageIndex{5}\): Mtihani wa pili wa derivative\(f(x)=x^5−5x^3.\)
\(x\)	\(f''(x)\)	Hitimisho
\ (x\) ">\(−\sqrt{3}\)	\ (f "(x)\)" >\(−30\sqrt{3}\)	Upeo wa mitaa
\ (x\) ">\(0\)	\ (f "(x)\)" >\(0\)	Pili derivative mtihani ni inconclusive
\ (x\) ">\(\sqrt{3}\)	\ (f "(x)\)" >\(30\sqrt{3}\)	Kima cha chini cha ndani

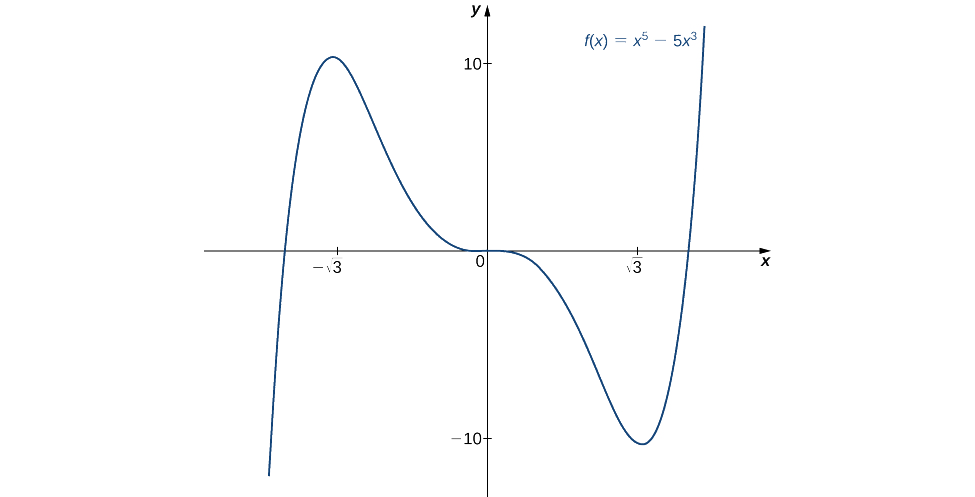
Kwa mtihani wa pili wa derivative, tunahitimisha kuwa\(f\) ina upeo wa ndani\(x=−\sqrt{3}\) na\(f\) una kiwango cha chini cha ndani\(x=\sqrt{3}\). pili derivative mtihani ni inconclusive katika\(x=0\). Kuamua kama\(f\) ina extrema ndani katika\(x=0,\) sisi kuomba kwanza derivative mtihani. Kutathmini ishara ya\(f'(x)=5x^2(x^2−3)\) kwa\(x∈(−\sqrt{3},0)\) na\(x∈(0,\sqrt{3})\), basi\(x=−1\) na\(x=1\) uwe pointi mbili za mtihani. Tangu\(f'(−1)<0\) na\(f'(1)<0\), tunahitimisha kuwa\(f\) inapungua kwa vipindi vyote na, kwa hiyo,\(f\) haina extrema ya ndani\(x=0\) kama inavyoonekana katika grafu ifuatayo.

Kazi f (x) = x5 - 5x3 imewekwa. Kazi huongezeka hadi (mizizi hasi ya mraba ya 3, 10), kisha hupungua kwa hatua ya kupunguka saa 0, inaendelea kupungua hadi (mizizi ya mraba ya 3, -10), na kisha huongezeka. — Takwimu:\(\PageIndex{10}\) Kazi\(f\) ina upeo wa ndani na\(x=−\sqrt{3}\) kiwango cha chini cha ndani\(x=\sqrt{3}\)

Zoezi\(\PageIndex{4}\)

Fikiria kazi\(f(x)=x^3−(\frac{3}{2})x^2−18x\). pointi\(c=3,\,−2\) kukidhi\(f'(c)=0\). Tumia mtihani wa pili wa derivative ili\(f\) uone ikiwa una kiwango cha juu cha ndani au cha chini cha ndani katika pointi hizo.

Kidokezo: \(f''(x)=6x−3\)

Jibu: \(f\)ina kiwango cha juu ndani katika\(−2\) na kiwango cha chini ndani katika\(3\).

Sasa tumeanzisha zana tunayohitaji kuamua ambapo kazi inakua na kupungua, pamoja na kupata ufahamu wa sura ya msingi ya grafu. Katika sehemu inayofuata sisi kujadili nini kinatokea kwa kazi kama\(x→±∞.\) Katika hatua hiyo, tuna zana za kutosha kutoa grafu sahihi ya aina kubwa ya kazi.

Dhana muhimu

Ikiwa\(c\) ni hatua muhimu ya\(f\) na\(f'(x)>0\) kwa\(x<c\) na\(f'(x)<0\) kwa\(x>c\), basi\(f\) ina upeo wa ndani\(c\).
Kama\(c\) ni hatua muhimu ya\(f\) na\(f'(x)<0\) kwa\(x<c\) na\(f'(x)>0\) kwa\(x>c,\) basi\(f\) ina kiwango cha chini ndani katika\(c\).
Ikiwa\(f''(x)>0\) zaidi ya muda\(I\), basi\(f\) ni concave juu\(I\).
Kama\(f''(x)<0\) zaidi ya muda\(I\), basi\(f\) ni concave chini juu\(I\).
Ikiwa\(f'(c)=0\) na\(f''(c)>0\), basi\(f\) ina kiwango cha chini cha ndani\(c\).
Ikiwa\(f'(c)=0\) na\(f''(c)<0\), basi\(f\) ina kiwango cha juu cha ndani\(c\).
Ikiwa\(f'(c)=0\) na\(f''(c)=0\), kisha tathmini\(f'(x)\) kwenye hatua\(x\) ya mtihani upande wa kushoto\(c\) na hatua ya mtihani\(x\) kwa haki ya\(c\), kuamua ikiwa\(f\) ina mwisho wa ndani\(c\).

faharasa

concave chini: kama\(f\) ni differentiable juu ya muda\(I\) na\(f'\) ni kupungua juu ya\(I\), basi\(f\) ni concave chini juu ya\(I\)

concave up: kama\(f\) ni differentiable juu ya muda\(I\) na\(f'\) ni kuongezeka juu ya\(I\), basi\(f\) ni concave juu ya\(I\)

concavity: Curve ya juu au ya chini ya grafu ya kazi

mtihani wa concavity: tuseme\(f\) ni mara mbili differentiable\(f''>0\) juu ya muda\(I\); kama juu ya\(I\), basi\(f\) ni concave juu\(I\); kama\(f''<\) juu\(I\), basi\(f\) ni concave chini juu\(I\)

mtihani wa kwanza wa derivative: hebu\(f\) iwe kazi inayoendelea juu ya kipindi\(I\) kilicho na hatua muhimu\(c\) kama hiyo\(f\) inavyoweza kutofautishwa\(I\) isipokuwa iwezekanavyo\(c\); ikiwa\(f'\) mabadiliko yanatokana na chanya hadi hasi kama\(x\) inavyoongezeka\(c\), basi \(f\)ina kiwango cha juu cha ndani\(c\); ikiwa\(f'\) mabadiliko yanatokana na hasi hadi chanya kama\(x\) inavyoongezeka kwa njia ya\(c\), basi\(f\) ina kiwango cha chini cha ndani\(c\); ikiwa\(f'\) haibadilika ishara kama\(x\) inavyoongezeka\(c\), basi\(f\) hana extremum ndani katika\(c\)

hatua ya kupindua: kama\(f\) ni kuendelea katika\(c\) na\(f\) mabadiliko concavity saa\(c\), uhakika\((c,f(c))\) ni hatua inflection ya\(f\)

pili derivative mtihani: tuseme\(f'(c)=0\) na\(f'\) 'ni kuendelea juu ya muda zenye\(c\); kama\(f''(c)>0\), basi\(f\) ina kiwango cha chini ndani katika\(c\); kama\(f''(c)<0\), basi\(f\) ina kiwango cha juu ndani katika\(c\); kama\(f''(c)=0\), basi mtihani ni inconclusive