4.4: Theorem ya Thamani ya Maana

Last updated
Save as PDF

Page ID: 178876

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Eleza maana ya theorem ya Rolle.
Eleza umuhimu wa Theorem ya Thamani ya Maana.
Hali matokeo matatu muhimu ya Theorem ya Theorem ya Thamani.

Theorem ya Thamani ya Maana ni mojawapo ya theorems muhimu zaidi katika calculus. Tunaangalia baadhi ya matokeo yake mwishoni mwa sehemu hii. Kwanza, hebu tuanze na kesi maalum ya Theorem ya Theorem ya Maana, inayoitwa Theorem ya Rolle.

Theorem ya Rolle

Kwa kawaida, theorem ya Rolle inasema kwamba ikiwa matokeo ya kazi tofauti$f$ ni sawa katika mwisho wa muda, basi kuna lazima iwe na hatua ya ndani$c$ ambapo$f'(c)=0$. Kielelezo$\PageIndex{1}$ unaeleza theorem hii.

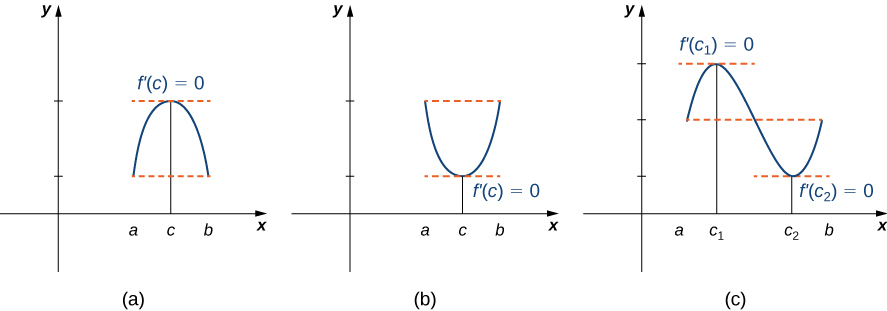
Takwimu imegawanywa katika sehemu tatu zilizoandikwa a, b, na c. takwimu inaonyesha roboduara ya kwanza na maadili a, c, na b alama kwenye x-axis. Parabola inayoelekea chini hutolewa kama maadili yake katika a na b ni sawa. Hatua c ni upeo wa kimataifa, na ni alibainisha kuwa f' (c) = 0. Kielelezo b inaonyesha roboduara ya kwanza na maadili a, c, na b alama kwenye x-axis. Parabola inayoelekea juu hutolewa kama maadili yake katika a na b ni sawa. Hatua c ni kiwango cha chini cha kimataifa, na ni alibainisha kuwa f' (c) = 0. Kielelezo c inaonyesha roboduara ya kwanza na pointi a, c1, c2, na b alama kwenye x-axis. Kipindi kimoja cha wimbi la sine hutolewa kama kwamba maadili yake katika a na b ni sawa. uhakika c1 ni upeo wa kimataifa, na ni alibainisha kuwa f' (c1) = 0. Hatua ya c2 ni kiwango cha chini cha kimataifa, na imeelezwa kuwa f' (c2) = 0. — Kielelezo$\PageIndex{1}$: Ikiwa kazi$f$ inayofahamika inatimiza$f(a)=f(b)$, basi derivative yake lazima iwe sifuri wakati fulani (s) kati$a$ na$b$.

Theorem ya Rolle

Hebu$f$ kuwa kazi inayoendelea juu ya muda uliofungwa$[a,b]$ na kutofautishwa juu ya muda wa wazi$(a,b)$ kama hiyo$f(a)=f(b)$. Kuna basi ipo angalau moja$c∈(a,b)$ ya kwamba$f'(c)=0.$

Ushahidi

Hebu$k=f(a)=f(b).$ tuangalie kesi tatu:

$f(x)=k$kwa ajili ya wote$x∈(a,b).$
Kuna$x∈(a,b)$ vile kwamba$f(x)>k.$
Kuna$x∈(a,b)$ vile kwamba$f(x)<k.$

Uchunguzi wa 1: Ikiwa$f(x)=k$ kwa wote$x∈(a,b)$, basi$f'(x)=0$ kwa wote$x∈(a,b).$

Uchunguzi 2: Kwa kuwa$f$ ni kazi inayoendelea juu ya muda uliofungwa, umefungwa$[a,b]$, na theorem ya thamani kali, ina kiwango cha juu kabisa. Pia, kwa kuwa kuna hatua kama$x∈(a,b)$ hiyo$f(x)>k$, kiwango cha juu kabisa ni kikubwa kuliko$k$. Kwa hiyo, upeo kabisa haufanyi wakati wa mwisho. Matokeo yake, kiwango cha juu kabisa kinapaswa kutokea katika hatua ya mambo ya ndani$c∈(a,b)$. Kwa sababu$f$ ina kiwango cha juu katika hatua ya mambo ya ndani$c$, na$f$ ni tofauti katika$c$, na theorem Fermat ya,$f'(c)=0.$

Uchunguzi 3: kesi wakati kuna uhakika$x∈(a,b)$ kama kwamba$f(x)<k$ ni sawa na kesi 2, na kiwango cha juu kubadilishwa na kiwango cha chini.

□

Jambo muhimu kuhusu theorem ya Rolle ni kwamba kutofautisha kwa kazi$f$ ni muhimu. Ikiwa$f$ haipatikani, hata kwa hatua moja, matokeo hayawezi kushikilia. Kwa mfano, kazi$f(x)=|x|−1$ ni kuendelea tena$[−1,1]$ na$f(−1)=0=f(1)$, lakini$f'(c)≠0$ kwa yoyote$c∈(−1,1)$ kama inavyoonekana katika takwimu zifuatazo.

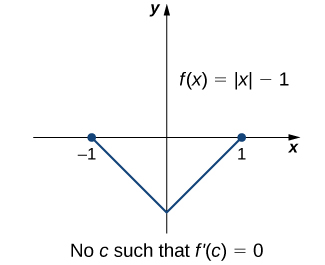
Kazi f (x) = |x| - 1 imewekwa. Inaonyeshwa kuwa f (1) = f (-1), lakini inabainishwa kuwa hakuna c kama f' (c) = 0. — Kielelezo$\PageIndex{2}$: Kwa kuwa$f(x)=|x|−1$ si tofauti katika$x=0$, hali ya theorem Rolle si kuridhika. Kwa kweli, hitimisho haina kushikilia hapa, hakuna$c∈(−1,1)$ vile kwamba$f'(c)=0.$

Hebu sasa tuchunguze kazi zinazotimiza masharti ya theorem ya Rolle na uhesabu wazi pointi$c$ ambapo$f'(c)=0.$

Mfano$\PageIndex{1}$: Using Rolle’s Theorem

Kwa kila moja ya kazi zifuatazo, hakikisha kwamba kazi inatimiza vigezo vilivyoelezwa katika theorem ya Rolle na kupata maadili yote$c$ katika kipindi kilichopewa ambapo$f'(c)=0.$

$f(x)=x^2+2x$juu ya$[−2,0]$
$f(x)=x^3−4x$juu ya$[−2,2]$

Suluhisho

a Tangu$f$ ni polynomial, ni kuendelea na kutofautishwa kila mahali. Aidha,$f(−2)=0=f(0).$ Kwa hiyo,$f$ satisfies vigezo vya theorem Rolle ya. Tunahitimisha kwamba kuna angalau thamani moja$c∈(−2,0)$ kama hiyo$f'(c)=0$. Kwa kuwa$f'(x)=2x+2=2(x+1),$ tunaona kwamba$f'(c)=2(c+1)=0$ ina maana$c=−1$ kama inavyoonekana katika grafu ifuatayo.

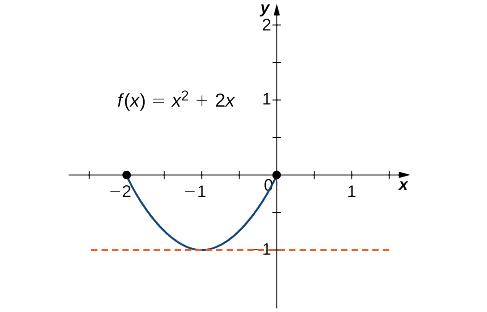
Kazi f (x) = x2 +2x imewekwa. Inaonyeshwa kuwa f (0) = f (-1), na mstari wa usawa uliopigwa hutolewa kwa kiwango cha chini kabisa saa (-1, -1). — Kielelezo$\PageIndex{3}$: Kazi hii ni ya kuendelea na kutofautishwa juu ya [-2,0],$f'(c)=0$ wakati$c=−1$.

b Kama katika sehemu a.$f$ ni polynomial na kwa hiyo ni kuendelea na kutofautishwa kila mahali. pia,$f(−2)=0=f(2).$ kwamba alisema,$f$ satisfies vigezo vya theorem Rolle ya. Kutofautisha, tunaona kwamba$f'(x)=3x^2−4.$ Kwa hiyo,$f'(c)=0$ wakati$x=±\frac{2}{\sqrt{3}}$. Vipengele vyote viwili viko katika kipindi$[−2,2]$, na kwa hiyo, pointi zote mbili zinakidhi hitimisho la theorem ya Rolle kama inavyoonekana kwenye grafu ifuatayo.

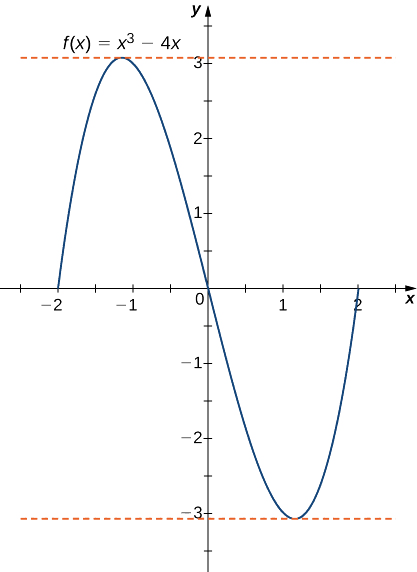
Kazi f (x) = x3 - 4x imewekwa. Ni dhahiri kwamba f (2) = f (ї 2) = f (0). Dashed mistari usawa ni inayotolewa katika x = ± 2/mizizi ya mraba ya 3, ambayo ni ya ndani ya kiwango cha juu na kiwango cha chini. — Kielelezo$\PageIndex{4}$: Kwa polynomial hii juu ya$[−2,2], f'(c)=0$ saa$x=±2/\sqrt{3}$.

Zoezi$\PageIndex{1}$

Thibitisha kwamba kazi$f(x)=2x^2−8x+6$ iliyoelezwa juu ya muda$[1,3]$ hutimiza masharti ya theorem ya Rolle. Kupata pointi zote$c$ uhakika na Theorem Rolle ya.

Kidokezo: Kupata maadili yote$c$, ambapo$f'(c)=0$.

Jibu: $c=2$

Theorem ya Thamani ya Maana na Maana Yake

Theorem ya Rolle ni kesi maalum ya Theorem ya Theorem ya Maana. Katika theorem ya Rolle, tunazingatia kazi tofauti$f$ ambazo ni sifuri katika mwisho. Theorem ya Thamani ya Maana huzalisha theorem ya Rolle kwa kuzingatia kazi ambazo si lazima zero katika mwisho. Kwa hiyo, tunaweza kuona Theorem ya Thamani ya Maana kama toleo lililopandwa la theorem ya Rolle (Kielelezo$\PageIndex{5}$). Theorem ya Thamani ya Maana inasema kwamba ikiwa$f$ inaendelea juu ya muda uliofungwa$[a,b]$ na kutofautishwa juu ya muda wa wazi$(a,b)$, basi kuna hatua$c∈(a,b)$ kama kwamba mstari wa tangent kwenye grafu ya$f$ at$c$ ni sawa na mstari wa kuunganisha $(a,f(a))$na$(b,f(b)).$

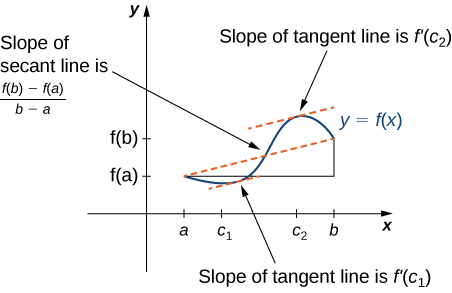
Kazi isiyo wazi ya sinusoidal y = f (x) hutolewa. Kwenye x-axis, a, c1, c2, na b ni alama. Kwenye mhimili wa y, f (a) na f (b) ni alama. Kazi f (x) huanza saa (a, f (a)), inapungua hadi c1, huongezeka hadi c2, na kisha hupungua hadi (b, f (b)). Mstari wa secant hutolewa kati ya (a, f (a)) na (b, f (b)), na inaelezwa kuwa mstari huu una mteremko (f (b) — f (a))/(b - a). Mstari wa tangent katika c1 na c2 hutolewa, na mistari hii ni sawa na mstari wa salama. Inasemekana kuwa mteremko wa mistari hii ya tangent ni f' (c1) na f' (c2), kwa mtiririko huo. — Kielelezo$\PageIndex{5}$: Theorem ya Thamani ya Maana inasema kuwa kwa kazi ambayo inakidhi masharti yake, wakati fulani mstari wa tangent una mteremko sawa na mstari wa salama kati ya mwisho. Kwa kazi hii, kuna maadili mawili$c_1$ na$c_2$ vile kwamba mstari wa tangent$f$ unaendelea$c_1$ na$c_2$ una mteremko sawa na mstari wa salama.

Maana Theorem Thamani

Hebu$f$ uendelee juu ya muda uliofungwa$[a,b]$ na kutofautishwa juu ya muda wa wazi$(a,b)$. Kisha, kuna angalau hatua moja$c∈(a,b)$ vile kwamba

\[f'(c)=\frac{f(b)−f(a)}{b−a} \nonumber \]

Ushahidi

Ushahidi unafuata kutoka theorem ya Rolle kwa kuanzisha kazi sahihi ambayo inatimiza vigezo vya theorem ya Rolle. Fikiria line kuunganisha$(a,f(a))$ na$(b,f(b)).$ Tangu mteremko wa mstari huo ni

\[\frac{f(b)−f(a)}{b−a} \nonumber \]

na mstari hupita kupitia hatua equation$(a,f(a)),$ ya mstari huo inaweza kuandikwa kama

\[y=\frac{f(b)−f(a)}{b−a}(x−a)+f(a). \nonumber \]

Hebu$g(x)$ kuashiria tofauti ya wima kati ya uhakika$(x,f(x))$ na uhakika$(x,y)$ kwenye mstari huo. Kwa hiyo,

\[g(x)=f(x)−\left[\frac{f(b)−f(a)}{b−a}(x−a)+f(a)\right]. \nonumber \]

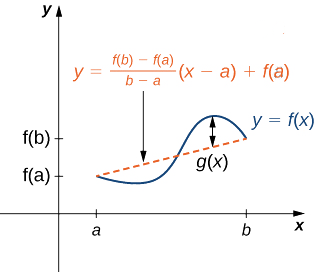$Kupanda lakini kusonga Curve Y sawa F ya X na mstari wa secant Y sawa F ya B minus F ya A kote B minus A pamoja F ya A, umbali kati ya Curve oscillating na mstari ni G ya X$ Kielelezo$\PageIndex{6}$: Thamani$g(x)$ ni tofauti ya wima kati ya uhakika$(x,f(x))$ na uhakika$(x,y)$ kwenye mstari wa salama unaounganisha$(a,f(a))$ na$(b,f(b))$.

Tangu grafu ya$f$ intersects line secant wakati$x=a$ na$x=b$, tunaona kwamba$g(a)=0=g(b)$. Kwa kuwa$f$ ni kazi differentiable juu$g$ ya$(a,b)$, pia ni kazi differentiable juu ya$(a,b)$. Zaidi ya hayo, tangu$f$ ni kuendelea juu$[a,b], \, g$ ya pia kuendelea juu ya$[a,b]$. Kwa hiyo,$g$ inakidhi vigezo vya theorem ya Rolle. Kwa hiyo, kuna uhakika$c∈(a,b)$ kwamba$g'(c)=0.$ Tangu

\[g'(x)=f'(x)−\frac{f(b)−f(a)}{b−a}, \nonumber \]

tunaona kwamba

\[g'(c)=f'(c)−\frac{f(b)−f(a)}{b−a}. \nonumber \]

Tangu$g'(c)=0,$ sisi kuhitimisha kwamba

\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

□

Katika mfano unaofuata, tunaonyesha jinsi Theorem ya Theorem ya Maana inaweza kutumika kwa kazi$f(x)=\sqrt{x}$ zaidi ya muda$[0,9]$. Njia hiyo ni sawa kwa kazi nyingine, ingawa wakati mwingine na matokeo ya kuvutia zaidi.

Mfano$\PageIndex{2}$: Verifying that the Mean Value Theorem Applies

Kwa$f(x)=\sqrt{x}$ zaidi ya muda$[0,9]$, onyesha kwamba$f$ inatimiza hypothesis ya Theorem ya Theorem ya Theorem ya Maana, na kwa hiyo kuna angalau thamani$c∈(0,9)$ moja ambayo$f′(c)$ ni sawa na mteremko wa mstari unaounganisha$(0,f(0))$ na$(9,f(9))$. Pata maadili haya$c$ yanayohakikishiwa na Theorem ya Thamani ya Maana.

Suluhisho

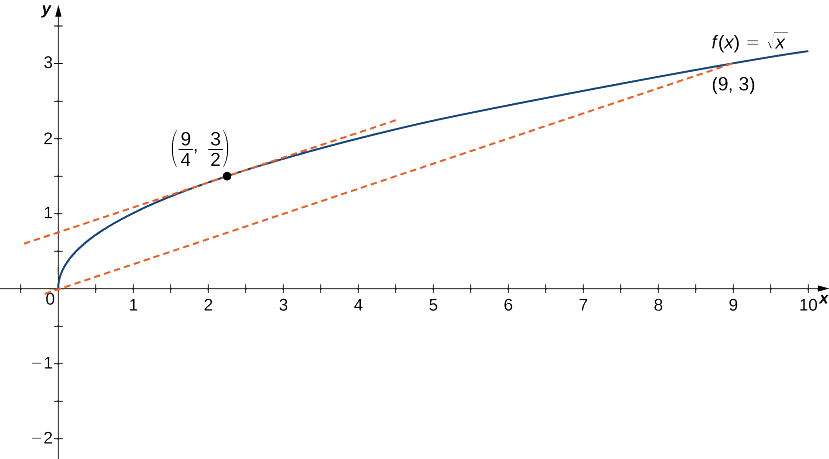
Tunajua kwamba$f(x)=\sqrt{x}$ ni kuendelea tena$[0,9]$ na kutofautisha juu$(0,9).$ Kwa hiyo,$f$ satisfies nadharia ya Theorem Mean Theorem Theorem, na kuna lazima kuwepo angalau thamani moja$c∈(0,9)$ kama kwamba$f′(c)$ ni sawa na mteremko wa mstari kuunganisha$(0,f(0))$ na$(9,f(9))$ (Kielelezo$\PageIndex{7}$). Kuamua ni thamani gani (s) ya$c$ ni uhakika, kwanza kuhesabu derivative ya$f$. Derivative$f′(x)=\frac{1}{(2\sqrt{x})}$. Mteremko wa mstari unaounganisha$(0,f(0))$ na$(9,f(9))$ hutolewa na

\[\frac{f(9)−f(0)}{9−0}=\frac{\sqrt{9}−\sqrt{0}}{9−0}=\frac{3}{9}=\frac{1}{3}. \nonumber \]

Tunataka kupata$c$ vile vile$f′(c)=\frac{1}{3}$. Hiyo ni, tunataka kupata$c$ vile kwamba

\[\frac{1}{2\sqrt{c}}=\frac{1}{3}. \nonumber \]

Kutatua equation hii kwa$c$, tunapata$c=\frac{9}{4}$. Kwa hatua hii, mteremko wa mstari wa tangent unafanana na mteremko wa mstari unaojiunga na mwisho.

Kazi f (x) = mizizi ya mraba ya x imewekwa kutoka (0, 0) hadi (9, 3). Kuna mstari wa secant inayotolewa kutoka (0, 0) hadi (9, 3). Kwa hatua (9/4, 3/2), kuna mstari wa tangent inayotolewa, na mstari huu ni sawa na mstari wa secant. — Kielelezo$\PageIndex{7}$: Mteremko wa mstari wa tangent$c=9/4$ ni sawa na mteremko wa sehemu ya mstari inayounganisha (0,0) na (9,3).

Programu moja ambayo husaidia kuonyesha Theorem ya Theorem ya Thamani inahusisha kasi. Kwa mfano, tuseme tunaendesha gari kwa saa 1 chini ya barabara moja kwa moja na kasi ya wastani ya 45 mph. Hebu$s(t)$ na$v(t)$ ueleze nafasi na kasi ya gari, kwa mtiririko huo, kwa$0≤t≤1$ h Kutokana kuwa kazi ya msimamo$s(t)$ ni tofauti, tunaweza kutumia Theorem ya Theorem ya Theorem ya Maana ili kuhitimisha kwamba$c∈(0,1)$, wakati fulani, kasi ya gari ilikuwa hasa

\[v(c)=s′(c)=\frac{s(1)−s(0)}{1−0}=45\,\text{mph.} \nonumber \]

Mfano$\PageIndex{3}$: Mean Value Theorem and Velocity

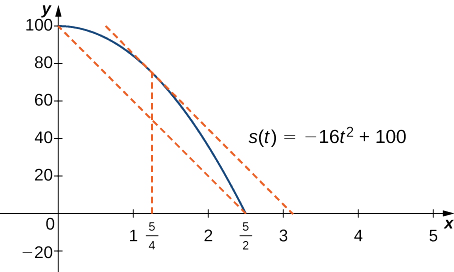
Ikiwa mwamba umeshuka kutoka kimo cha ft 100, msimamo wake$t$ sekunde baada ya kushuka hadi unapopiga ardhi hutolewa na kazi$s(t)=−16t^2+100.$

Kuamua muda gani inachukua kabla ya mwamba kugonga ardhi.
Pata kasi ya wastani$v_{avg}$ ya mwamba kwa wakati mwamba unatolewa na mwamba hupiga ardhi.
Kupata muda$t$ uhakika na Theorem Mean Thamani wakati kasi instantaneous ya mwamba ni$v_{avg}.$

Suluhisho

a Wakati mwamba hupiga ardhi, msimamo wake ni$s(t)=0$. Kutatua equation$−16t^2+100=0$ kwa$t$, tunaona kwamba$t=±\frac{5}{2}sec$. Kwa kuwa tunazingatia tu$t≥0$, mpira utapiga$\frac{5}{2}$ sekunde ya ardhi baada ya kushuka.

b. kasi ya wastani hutolewa na

\[v_{avg}=\frac{s(5/2)−s(0)}{5/2−0}=\frac{0−100}{5/2}=−40\,\text{ft/sec}. \nonumber \]

c. kasi instantaneous hutolewa na derivative ya kazi nafasi. Kwa hiyo, tunahitaji kupata muda$t$ kama vile$v(t)=s′(t)=v_{avg}=−40$ ft/sec. Kwa kuwa$s(t)$ ni kuendelea juu ya muda$[0,5/2]$ na$(0,5/2),$ kutofautishwa zaidi ya muda na Theorem Maana Theorem Theorem, kuna uhakika kuwa na uhakika$c∈(0,5/2)$ kama kwamba

\[s′(c)=\frac{s(5/2)−s(0)}{5/2−0}=−40. \nonumber \]

Kuchukua derivative ya kazi nafasi$s(t)$, tunaona kwamba$s′(t)=−32t.$ Kwa hiyo, equation inapunguza kwa$s′(c)=−32c=−40.$ Kutatua equation hii kwa$c$, tuna$c=\frac{5}{4}$. Kwa hiyo,$\frac{5}{4}$ sec baada ya mwamba imeshuka, kasi ya instantaneous inalingana na kasi ya wastani ya mwamba wakati wa kuanguka kwake bure:$−40$ ft/sec.

Kazi s (t) = -16t2 + 100 imewekwa kutoka (0, 100) hadi (5/2, 0). Kuna mstari wa secant inayotolewa kutoka (0, 100) hadi (5/2, 0). Katika hatua inayohusiana na x = 5/4, kuna mstari wa tangent inayotolewa, na mstari huu ni sawa na mstari wa secant. — Kielelezo$\PageIndex{8}$: Wakati wa$t=5/4$ sekunde, kasi ya mwamba ni sawa na kasi yake ya wastani kutoka wakati imeshuka mpaka inapiga ardhi.

Zoezi$\PageIndex{2}$

Tuseme mpira umeshuka kutoka urefu wa ft 200. Msimamo wake$t$ kwa wakati ni$s(t)=−16t^2+200.$ Kupata$t$ wakati ambapo kasi instantaneous ya mpira ni sawa na kasi yake ya wastani.

Kidokezo: Kwanza, onyesha muda gani inachukua kwa mpira kugonga chini. Kisha, pata kasi ya wastani ya mpira kutoka wakati imeshuka mpaka inapiga ardhi.

Jibu: $\frac{5}{2\sqrt{2}}$sekunde

Corollaries ya Theorem ya Thamani ya Maana

Hebu sasa tuangalie corollaries tatu za Theorem ya Theorem ya Maana. Matokeo haya yana matokeo muhimu, ambayo tunatumia katika sehemu zijazo.

Kwa hatua hii, tunajua derivative ya kazi yoyote ya mara kwa mara ni sifuri. Theorem ya Thamani ya Maana inatuwezesha kuhitimisha kwamba kuzungumza pia ni kweli. Hasa, ikiwa$f′(x)=0$ kwa wote$x$ kwa muda fulani$I$, basi$f(x)$ ni mara kwa mara juu ya muda huo. Matokeo haya yanaweza kuonekana intuitively dhahiri, lakini ina maana muhimu ambayo si dhahiri, na sisi kujadili yao kwa muda mfupi.

Corollary 1: Kazi na derivative ya sifuri

Hebu$f$ iwe tofauti zaidi ya muda$I$. Ikiwa$f′(x)=0$ kwa wote$x∈I$, basi$f(x)=$ mara kwa mara kwa wote$x∈I.$

Ushahidi

Kwa kuwa$f$ ni differentiable juu ya$I$,$f$ lazima kuendelea juu ya$I$. Tuseme$f(x)$ si mara kwa mara kwa wote$x$ katika$I$. Kisha kuna kuwepo$a,b∈I$, wapi$a≠b$ na$f(a)≠f(b).$ Chagua nukuu ili$a<b.$ Kwa hiyo,

\[\frac{f(b)−f(a)}{b−a}≠0. \nonumber \]

Kwa kuwa$f$ ni kazi tofauti, na Theorem ya Theorem ya Thamani ya Maana, kuna$c∈(a,b)$ vile vile

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Kwa hiyo, kuna$c∈I$ vile vile$f′(c)≠0$, ambayo inapingana na dhana kwamba$f′(x)=0$ kwa wote$x∈I$.

□

Kutoka “Corollary 1: Kazi na derivative ya Zero,” inafuata kwamba ikiwa kazi mbili zina derivative sawa, zinatofautiana na, zaidi, mara kwa mara.

Corollary 2: Theorem ya Tofauti ya Mara kwa mara

Ikiwa$f$ na$g$ ni tofauti zaidi ya muda$I$ na$f′(x)=g′(x)$ kwa wote$x∈I$, basi$f(x)=g(x)+C$ kwa mara kwa mara$C$.

Ushahidi

Hebu$h(x)=f(x)−g(x).$ basi,$h′(x)=f′(x)−g′(x)=0$$x∈I.$ kwa wote By Corollary 1, kuna mara kwa mara$C$ kama kwamba$h(x)=C$ kwa wote$x∈I$. Kwa hiyo,$f(x)=g(x)+C$ kwa wote$x∈I.$

□

Corollary ya tatu ya Theorem ya Thamani ya Maana inazungumzia wakati kazi inaongezeka na inapungua. Kumbuka kwamba kazi$f$ ni kuongeza juu ya$I$ kama$f(x_1)<f(x_2)$ wakati wowote$x_1<x_2$, ambapo$f$ ni kupungua juu ya$I$ kama$f(x_1)>f(x_2)$ wakati wowote$x_1<x_2$. Kutumia Theorem ya Thamani ya Maana, tunaweza kuonyesha kwamba ikiwa derivative ya kazi ni chanya, basi kazi inaongezeka; ikiwa derivative ni hasi, basi kazi inapungua (Kielelezo$\PageIndex{9}$). Tunatumia ukweli huu katika sehemu inayofuata, ambapo tunaonyesha jinsi ya kutumia derivative ya kazi ili kupata maadili ya kiwango cha juu na cha chini cha kazi, na jinsi ya kuamua sura ya grafu.

Ukweli huu ni muhimu kwa sababu ina maana kwamba kwa ajili ya kazi fulani$f$, kama kuna kazi$F$ kama kwamba$F′(x)=f(x)$; kisha, tu kazi nyingine ambayo derivative sawa na$f$ ni kwa baadhi$F(x)+C$ ya mara kwa mara$C$. Tunajadili matokeo haya kwa undani zaidi baadaye katika sura.

Kazi isiyo wazi ya sinusoidal f (x) imewekwa. Inaongezeka kutoka mahali fulani katika roboduara ya pili hadi (a, f (a)). Katika sehemu hii ni alibainisha kuwa f' — Kielelezo$\PageIndex{9}$: Ikiwa kazi ina derivative chanya juu ya muda fulani$I$, basi kazi huongezeka zaidi ya muda$I$ huo; ikiwa derivative ni hasi kwa muda fulani$I$, basi kazi inapungua zaidi ya muda huo$I$.

Corollary 3: Kuongezeka na Kupungua Kazi

Hebu$f$ uendelee juu ya muda uliofungwa$[a,b]$ na kutofautishwa juu ya muda wa wazi$(a,b)$.

Ikiwa$f′(x)>0$ kwa wote$x∈(a,b)$, basi$f$ ni kazi inayoongezeka$[a,b].$
Ikiwa$f′(x)<0$ kwa wote$x∈(a,b)$, basi$f$ ni kazi ya kupungua$[a,b].$

Ushahidi

Sisi kuthibitisha i.; ushahidi wa ii. ni sawa. Tuseme$f$ si kazi kuongeza juu ya$I$. Kisha kuna kuwepo$a$ na$b$ katika$I$ vile$a<b$, lakini$f(a)≥f(b)$. Kwa kuwa$f$ ni kazi differentiable juu ya$I$, na Theorem Mean Theorem Theorem kuna$c∈(a,b)$ vile kwamba

\[f′(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \]

Tangu$f(a)≥f(b)$, tunajua kwamba$f(b)−f(a)≤0$. Pia,$a<b$ inatuambia kwamba$b−a>0.$ Sisi kuhitimisha kwamba

\[f′(c)=\frac{f(b)−f(a)}{b−a}≤0. \nonumber \]

Hata hivyo,$f′(x)>0$ kwa wote$x∈I$. Hii ni utata, na kwa hiyo$f$ lazima iwe kazi inayoongezeka$I$.

□

Dhana muhimu

Kama$f$ ni kuendelea tena$[a,b]$ na kutofautisha tena$(a,b)$ na$f(a)=f(b)$, basi kuna uhakika$c∈(a,b)$ kama kwamba$f′(c)=0.$ Hii ni theorem Rolle ya.
Ikiwa$f$ inaendelea tena$[a,b]$ na kutofautishwa juu$(a,b)$, basi kuna uhakika$c∈(a,b)$ kama kwamba\[f'(c)=\frac{f(b)−f(a)}{b−a}. \nonumber \] Hii ni Theorem ya Thamani ya Maana.
Ikiwa$f'(x)=0$ zaidi ya muda$I$, basi$f$ ni mara kwa mara juu$I$.
Ikiwa kazi mbili za kutofautisha$f$ na$g$ kukidhi$f′(x)=g′(x)$ zaidi$I$, basi$f(x)=g(x)+C$ kwa mara kwa mara$C$.
Ikiwa$f′(x)>0$ zaidi ya muda$I$, basi$f$ inaongezeka zaidi$I$. Ikiwa$f′(x)<0$ juu$I$, basi$f$ inapungua$I$.

faharasa

maana theorem thamani: kama$f$ ni kuendelea juu$[a,b]$ na differentiable juu$(a,b)$, basi kuna$c∈(a,b)$ vile kwamba$f′(c)=\frac{f(b)−f(a)}{b−a}$

theorem ya roller: kama$f$ ni kuendelea juu$[a,b]$ na differentiable juu$(a,b)$$f(a)=f(b)$, na kama, basi kuna$c∈(a,b)$ vile kwamba$f′(c)=0$