4.3: Maxima na Minima

Last updated
Save as PDF

Page ID: 178854

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Kufafanua extrema kabisa.
Eleza extrema ya ndani.
Eleza jinsi ya kupata pointi muhimu za kazi juu ya muda uliofungwa.
Eleza jinsi ya kutumia pointi muhimu ili kupata extrema kabisa juu ya muda uliofungwa.

Kutokana na kazi fulani, mara nyingi tunavutiwa na kuamua maadili makubwa na madogo ya kazi. Taarifa hii ni muhimu katika kujenga grafu sahihi. Kupata maadili ya kiwango cha juu na cha chini ya kazi pia ina umuhimu wa vitendo, kwa sababu tunaweza kutumia njia hii kutatua matatizo ya uboreshaji, kama vile kuongeza faida, kupunguza kiasi cha vifaa vinavyotumiwa katika utengenezaji wa alumini unaweza, au kutafuta urefu wa juu wa roketi inaweza kufikia. Katika sehemu hii, tunaangalia jinsi ya kutumia derivatives ili kupata maadili makubwa na madogo zaidi ya kazi.

Extrema kabisa

Fikiria kazi\(f(x)=x^2+1\) juu ya muda\((−∞,∞)\). Kama\(x→±∞, f(x)→∞\). Kwa hiyo, kazi haina thamani kubwa. Hata hivyo, tangu\(x^2+1≥1\) kwa idadi zote halisi\(x\) na\(x^2+1=1\) wakati\(x=0\), kazi ina thamani ndogo\(1\), wakati\(x=0\). Tunasema kwamba\(1\) ni kiwango cha chini kabisa cha\(f(x)=x^2+1\) na hutokea katika\(x=0\). Tunasema kwamba\(f(x)=x^2+1\) haina kiwango cha juu kabisa (Kielelezo\(\PageIndex{1}\)).

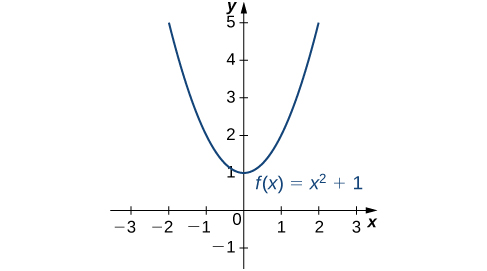
Kazi f (x) = x ^ 2 + 1 imewekwa, na kiwango cha chini cha 1 kinaonekana kuwa x = 0. — Kielelezo\(\PageIndex{1}\): Kazi iliyotolewa ina kiwango cha chini kabisa cha\(1\) saa\(x=0\). Kazi haina kiwango cha juu kabisa.

ufafanuzi: Extrema kabisa

Hebu\(f\) kuwa kazi defined juu ya muda\(I\) na basi\(c∈I\). Tunasema\(f\) ina kiwango cha juu kabisa juu ya\(I\) saa\(c\) kama\(f(c)≥f(x)\) kwa ajili ya wote\(x∈I\). Tunasema\(f\) ina kiwango cha chini kabisa juu ya\(I\) saa\(c\) kama\(f(c)≤f(x)\) kwa ajili ya wote\(x∈I\). Kama\(f\) ina kiwango cha juu kabisa juu ya\(I\) saa\(c\) au kiwango cha chini kabisa juu ya\(I\) saa\(c\), tunasema\(f\) ina extremum kabisa juu ya\(I\) saa\(c\).

Kabla ya kuendelea, hebu tuangalie masuala mawili muhimu kuhusu ufafanuzi huu. Kwanza, neno kabisa hapa halirejelea thamani kamili. Mwisho kamili unaweza kuwa chanya, hasi, au sifuri. Pili, kama kazi\(f\) ina extremum kabisa juu ya muda\(I\) katika\(c\), extremum kabisa ni\(f(c)\). Nambari halisi\(c\) ni hatua katika uwanja ambapo extremum kabisa hutokea. Kwa mfano, fikiria kazi\(f(x)=1/(x^2+1)\) juu ya muda\((−∞,∞)\). Tangu

\[f(0)=1≥\frac{1}{x^2+1}=f(x) \nonumber \]

kwa idadi yote halisi\(x\), tunasema\(f\) ina kiwango cha juu kabisa juu ya\((−∞,∞)\) saa\(x=0\). Upeo kabisa ni\(f(0)=1\). Inatokea katika\(x=0\), kama inavyoonekana katika Kielelezo\(\PageIndex{2}\) (b).

Kazi inaweza kuwa na kiwango cha juu kabisa na kiwango cha chini kabisa, extremum moja tu, au wala. Kielelezo\(\PageIndex{2}\) inaonyesha kazi kadhaa na baadhi ya uwezekano tofauti kuhusu extrema kabisa. Hata hivyo, theorem ifuatayo, inayoitwa Theorem ya Theorem ya Theorem ya Theorem, inathibitisha kuwa kazi inayoendelea\(f\) juu ya muda uliofungwa, imefungwa\([a,b]\) ina kiwango cha juu kabisa na kiwango cha chini kabisa.

Takwimu hii ina sehemu sita a, b, c, d, e, na f Katika takwimu a, mstari f (x) = x ^ 3 unaonyeshwa, na inaelezwa kuwa haina kiwango cha chini kabisa na hakuna kiwango cha juu kabisa. Katika takwimu b, mstari f (x) = 1/ (x ^ 2 + 1) unaonyeshwa, ambayo iko karibu na 0 kwa urefu wake zaidi na huongezeka hadi mapema saa (0, 1); haina kiwango cha chini kabisa, lakini ina kiwango cha juu kabisa cha 1 saa x = 0. Katika takwimu c, mstari f (x) = cos x inavyoonyeshwa, ambayo ina kiwango cha chini kabisa cha -1 saa ± π, ± 3π,... na kiwango cha juu kabisa cha 1 saa 0, ± 2π, ± 4π,... Katika takwimu d, kazi ya kipande f (x) = 2 - x ^ 2 kwa 0 ≤ x <2 na x - 3 kwa 2 ≤ x ≤ 4 inavyoonyeshwa, na kiwango cha juu kabisa cha 2 saa x = 0 na hakuna kiwango cha chini kabisa. Katika takwimu e, kazi f (x) = (x - 2) 2 inavyoonekana kwenye [1, 4], ambayo ina kiwango cha juu kabisa cha 4 saa x = 4 na kiwango cha chini kabisa cha 0 saa x = 2. Katika takwimu f, kazi f (x) = x/ (2 - x) inavyoonekana kwenye [0, 2), na kiwango cha chini kabisa cha 0 saa x = 0 na hakuna kiwango cha juu kabisa. — Kielelezo\(\PageIndex{2}\): Grafu (a), (b), na (c) zinaonyesha uwezekano kadhaa wa extrema kabisa kwa kazi na uwanja wa\((−∞,∞).\) Grafu (d), (e), na (f) zinaonyesha uwezekano kadhaa wa extrema kabisa kwa kazi na uwanja ambao ni muda uliopangwa.

Theorem\(\PageIndex{1}\): Extreme Value Theorem

Ikiwa\(f\) ni kazi inayoendelea juu ya muda uliofungwa\([a,b]\), umefungwa, basi kuna\([a,b]\) hatua ambayo\(f\) ina kiwango cha juu kabisa\([a,b]\) na kuna\([a,b]\) hatua ambayo\(f\) ina kiwango cha chini kabisa\([a,b]\).

Ushahidi wa theorem ya thamani uliokithiri ni zaidi ya upeo wa maandishi haya. Kwa kawaida, inathibitishwa katika kozi juu ya uchambuzi halisi. Kuna pointi kadhaa muhimu za kumbuka kuhusu taarifa ya theorem hii. Kwa theorem ya thamani uliokithiri kuomba, kazi lazima iendelee juu ya muda uliofungwa, uliowekwa. Ikiwa muda\(I\) unafunguliwa au kazi ina hata hatua moja ya kuacha, kazi inaweza kuwa na kiwango cha juu kabisa au kiwango cha chini kabisa\(I\). Kwa mfano, fikiria kazi zilizoonyeshwa kwenye Kielelezo\(\PageIndex{2}\) (d), (e), na (f). Kazi zote tatu hizi hufafanuliwa juu ya vipindi vilivyofungwa. Hata hivyo, kazi katika grafu (e) ni pekee ambayo ina kiwango cha juu kabisa na kiwango cha chini kabisa juu ya uwanja wake. Theorem thamani uliokithiri haiwezi kutumika kwa kazi katika grafu (d) na (f) kwa sababu hakuna kazi hizi ni kuendelea juu ya muda imefungwa, imepakana. Ingawa kazi katika grafu (d) inafafanuliwa juu ya muda uliofungwa\([0,4]\), kazi hiyo inakoma\(x=2\). Kazi ina kiwango cha juu kabisa\([0,4]\) lakini haina kiwango cha chini kabisa. Kazi katika grafu (f) inaendelea juu ya kipindi cha nusu ya wazi\([0,2)\), lakini haijafafanuliwa\(x=2\), na kwa hiyo haiendelei juu ya muda uliofungwa, uliowekwa. Kazi ina kiwango cha chini kabisa juu ya\([0,2)\), lakini haina kiwango cha juu kabisa\([0,2)\). Grafu hizi mbili zinaonyesha kwa nini kazi juu ya muda imepakana inaweza kushindwa kuwa na kiwango cha juu kabisa na/au kiwango cha chini kabisa.

Kabla ya kuangalia jinsi ya kupata extrema kabisa, hebu tuchunguze dhana inayohusiana ya extrema ya ndani. Wazo hili ni muhimu katika kuamua wapi extrema kabisa hutokea.

Extrema za Mitaa na Pointi muhimu

Fikiria kazi\(f\) iliyoonyeshwa kwenye Kielelezo\(\PageIndex{3}\). Grafu inaweza kuelezewa kama milima miwili yenye bonde katikati. Thamani ya juu kabisa ya kazi hutokea kwenye kilele cha juu, saa\(x=2\). Hata hivyo, pia\(x=0\) ni hatua ya riba. Ingawa\(f(0)\) si thamani kubwa ya\(f\), thamani\(f(0)\) ni kubwa kuliko\(f(x)\) kwa wote\(x\) karibu 0. Tunasema\(f\) ina kiwango cha juu ndani katika\(x=0\). Vile vile, kazi\(f\) haina kiwango cha chini kabisa, lakini ina kiwango cha chini cha ndani kwa\(x=1\) sababu\(f(1)\) ni chini\(f(x)\) ya\(x\) karibu 1.

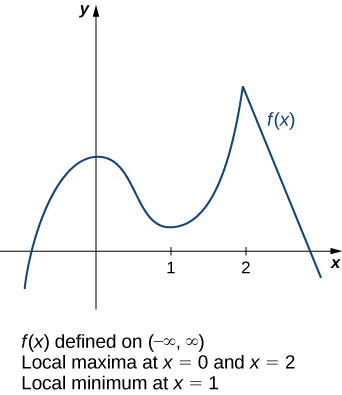
Kazi f (x) inavyoonekana, ambayo hupanda juu kutoka roboduara III, hupungua kwa roboduara II, kufikia upeo wa ndani kwenye mhimili wa y, hupungua kufikia kiwango cha chini ndani katika roboduara I x = 1, huongezeka hadi kiwango cha juu cha ndani katika x = 2 ambayo ni kubwa kuliko kiwango cha juu cha ndani, na kisha hupungua kwa kasi kupitia roboduara IV. — Kielelezo\(\PageIndex{3}\): Kazi hii\(f\) ina maxima mbili za mitaa na kiwango cha chini cha ndani. Upeo wa ndani pia\(x=2\) ni upeo kabisa.

Ufafanuzi: Extrema ya Mitaa

Kazi\(f\) ina upeo wa ndani\(c\) ikiwa kuna muda wa wazi unao na\(c\) vile\(I\)\(I\) vilivyomo katika uwanja wa\(f\) na\(f(c)≥f(x)\) kwa wote\(x∈I\). Kazi\(f\) ina kiwango cha chini cha ndani\(c\) ikiwa kuna muda wa wazi unao na\(c\) vile\(I\)\(I\) vilivyomo katika uwanja wa\(f\) na\(f(c)≤f(x)\) kwa wote\(x∈I\). kazi\(f\) ina extremum ndani katika\(c\) kama\(f\) ina upeo wa ndani katika\(c\) au\(f\) ina kiwango cha chini ndani katika\(c\).

Kumbuka kwamba ikiwa\(f\) ina kiwango cha mwisho kabisa\(c\) na\(f\) kinaelezwa juu ya muda ulio na\(c\), basi pia\(f(c)\) inachukuliwa kuwa mwisho wa ndani. Kama extremum kabisa kwa ajili ya kazi\(f\) hutokea katika endpoint, hatuwezi kufikiria kwamba kuwa extremum ndani, lakini badala yake rejea kwamba kama mwisho extremum.

Kutokana na grafu ya kazi\(f\), wakati mwingine ni rahisi kuona ambapo kiwango cha juu cha ndani au cha chini kinatokea. Hata hivyo, si rahisi kuona kila wakati, kwa kuwa vipengele vya kuvutia kwenye grafu ya kazi hazionekani kwa sababu hutokea kwa kiwango kidogo sana. Pia, hatuwezi kuwa na grafu ya kazi. Katika kesi hizi, jinsi gani tunaweza kutumia formula kwa ajili ya kazi ya kuamua ambapo extrema hizi kutokea?

Ili kujibu swali hili, hebu tuangalie Kielelezo\(\PageIndex{3}\) tena. extrema mitaa kutokea katika\(x=0, x=1,\) na\(x=2.\) Taarifa kwamba katika\(x=0\) na\(x=1\), derivative\(f'(x)=0\). Katika\(x=2\), derivative\(f'(x)\) haipo, kwani kazi\(f\) ina kona huko. Kwa kweli, ikiwa\(f\) ina extremum ya ndani kwa hatua\(x=c\), derivative\(f'(c)\) lazima kukidhi mojawapo ya masharti yafuatayo: ama\(f'(c)=0\) au\(f'(c)\) haijulikani. Thamani hiyo\(c\) inajulikana kama hatua muhimu na ni muhimu katika kutafuta maadili uliokithiri kwa kazi.

Ufafanuzi: Pointi muhimu

Hebu\(c\) kuwa hatua ya mambo ya ndani katika uwanja wa\(f\). Tunasema kwamba\(c\) ni hatua muhimu ya\(f\) kama\(f'(c)=0\) au\(f'(c)\) haijulikani.

Kama ilivyoelezwa hapo awali, kama\(f\) ina extremum mitaa katika hatua\(x=c\), basi\(c\) lazima hatua muhimu ya\(f\). Ukweli huu unajulikana kama theorem ya Fermat.

Theorem\(\PageIndex{2}\): Fermat’s Theorem

Kama\(f\) ina extremum ndani ya saa\(c\) na\(f\) ni differentiable katika\(c\), basi\(f'(c)=0.\)

Ushahidi

Tuseme\(f\) ina extremum ndani katika\(c\) na\(f\) ni kutofautishwa katika\(c\). Tunahitaji kuonyesha kwamba\(f'(c)=0\). Ili kufanya hivyo, tutaonyesha kwamba\(f'(c)≥0\) na\(f'(c)≤0\), na kwa hiyo\(f'(c)=0\). Kwa kuwa\(f\) ina extremum ndani katika\(c\),\(f\) ina kiwango cha juu ndani au ndani ya chini katika\(c\). Tuseme\(f\) ina kiwango cha juu ndani katika\(c\). Kesi ambayo\(f\) ina kiwango cha chini cha ndani\(c\) inaweza kushughulikiwa sawa. Hapo basi kuna muda wa wazi mimi kama kwamba\(f(c)≥f(x)\) kwa wote\(x∈I\). Tangu\(f\) ni differentiable katika\(c\), kutokana na ufafanuzi wa derivative, tunajua kwamba

\[f'(c)=\lim_{x→c}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Kwa kuwa kikomo hiki kipo, mipaka yote ya upande mmoja pia iko na sawa\(f'(c)\). Kwa hiyo,

\[f'(c)=\lim_{x→c^+}\frac{f(x)−f(c)}{x−c,}\label{FermatEqn2} \]

\[f'(c)=\lim_{x→c^−}\frac{f(x)−f(c)}{x−c}. \nonumber \]

Kwa kuwa\(f(c)\) ni upeo wa ndani, tunaona kwamba\(f(x)−f(c)≤0\) kwa\(x\) karibu\(c\). Kwa hiyo, kwa\(x\) karibu\(c\), lakini\(x>c\), tuna\(\frac{f(x)−f(c)}{x−c}≤0\). Kutoka Equation\ ref {FermateQn2} tunahitimisha kuwa\(f'(c)≤0\). Vile vile, inaweza kuonyeshwa kwamba\(f'(c)≥0.\) Kwa hiyo,\(f'(c)=0.\)

□

Kutoka theorem ya Fermat, tunahitimisha kwamba ikiwa\(f\) ina mwisho wa ndani\(c\), basi ama\(f'(c)=0\) au\(f'(c)\) haijulikani. Kwa maneno mengine, extrema ya ndani inaweza kutokea tu kwa pointi muhimu.

Kumbuka theorem hii haina madai kwamba kazi\(f\) lazima iwe na extremum ya ndani katika hatua muhimu. Badala yake, inasema kuwa pointi muhimu ni wagombea wa extrema za mitaa. Kwa mfano, fikiria kazi\(f(x)=x^3\). Tuna\(f'(x)=3x^2=0\) wakati\(x=0\). Kwa hiyo,\(x=0\) ni hatua muhimu. Hata hivyo,\(f(x)=x^3\) ni kuongeza juu ya\((−∞,∞)\), na hivyo\(f\) hana extremum ndani katika\(x=0\). Katika Kielelezo\(\PageIndex{4}\), tunaona uwezekano tofauti wa pointi muhimu. Katika baadhi ya matukio haya, kazi zina extrema za mitaa katika pointi muhimu, wakati katika hali nyingine kazi hazifanyi. Kumbuka kuwa grafu hizi hazionyeshe uwezekano wote wa tabia ya kazi katika hatua muhimu.

Takwimu hii ina sehemu tano a, b, c, d, na e Katika takwimu a, parabola inavyoonekana inakabiliwa chini katika roboduara I; kuna mstari wa usawa wa tangent kwenye kiwango cha juu cha alama ya f' (c) = 0. Katika takwimu b, kuna kazi inayotolewa na asymptote katika c, maana kwamba kazi huongezeka kuelekea infinity pande zote mbili za c; inaelezwa kuwa f' (c) haijulikani. Katika takwimu c, toleo la grafu ya thamani kamili inavyoonyeshwa ambayo imebadilishwa ili kiwango cha chini chake kiwe katika quadrant I na x = c Inasemekana kuwa f' (c) haijulikani. Katika Kielelezo d, toleo la kazi f (x) = x ^ 3 linaonyeshwa ambayo imebadilishwa ili hatua yake ya kupindua iko katika roboduara I na x = c. hatua yake ya kupindua katika (c, f (c)) ina mstari wa usawa kwa njia hiyo, na inaelezwa kuwa f' (c) = 0. Katika Kielelezo e, toleo la kazi f (x) = x1/3 linaonyeshwa ambalo limebadilishwa ili hatua yake ya kupindua iko katika roboduara I na x = c. hatua yake ya kupindua katika (c, f (c)) ina mstari wa wima kupitia hiyo, na inaelezwa kuwa f' (c) haijulikani. — Kielelezo\(\PageIndex{4}\): (—e) kazi\(f\) ina hatua muhimu katika\(c\) kama\(f'(c)=0\) au\(f'(c)\) ni undefined. Kazi inaweza au isiwe na extremum ya ndani katika hatua muhimu.

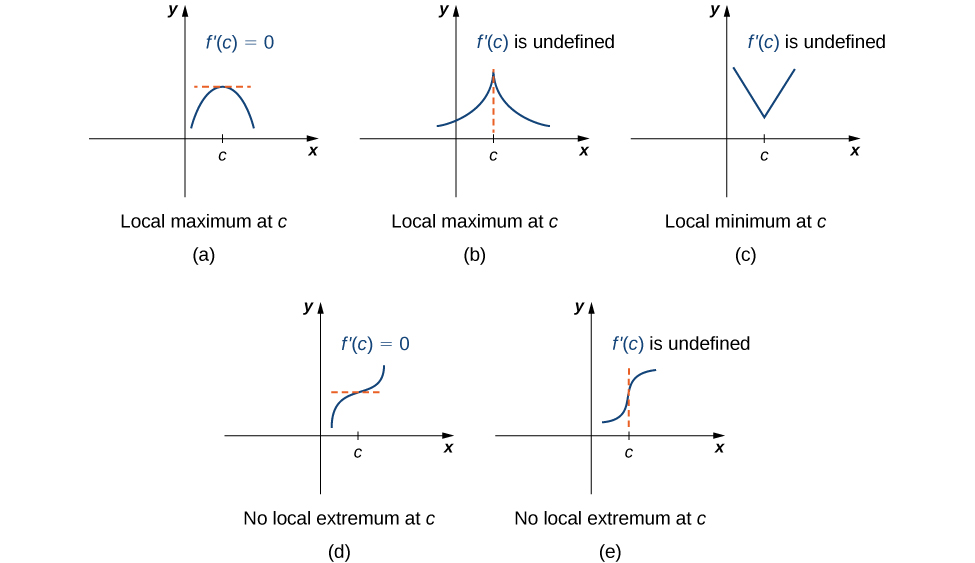
Baadaye katika sura hii tunaangalia mbinu za uchambuzi kwa kuamua kama kazi kweli ina extremum mitaa katika hatua muhimu. Kwa sasa, hebu tugeuke mawazo yetu ili kupata pointi muhimu. Tutatumia uchunguzi wa kielelezo ili kuamua kama hatua muhimu inahusishwa na extremum ya ndani.

Mfano\(\PageIndex{1}\): Locating Critical Points

Kwa kila kazi zifuatazo, pata pointi zote muhimu. Tumia matumizi ya graphing ili kuamua kama kazi ina extremum ya ndani katika kila moja ya pointi muhimu.

\(f(x)=\frac{1}{3}x^3−\frac{5}{2}x^2+4x\)
\(f(x)=(x^2−1)^3\)
\(f(x)=\frac{4x}{1+x^2}\)

Suluhisho

a. derivative\(f'(x)=x^2−5x+4\) hufafanuliwa kwa idadi yote halisi\(x\). Kwa hiyo, tunahitaji tu kupata maadili kwa\(x\) wapi\(f'(x)=0\). Kwa kuwa\(f'(x)=x^2−5x+4=(x−4)(x−1)\), pointi muhimu ni\(x=1\) na\(x=4.\) Kutoka kwenye grafu ya\(f\) katika Kielelezo\(\PageIndex{5}\), tunaona kwamba\(f\) ina upeo wa ndani\(x=1\) na kiwango cha chini cha ndani\(x=4\).

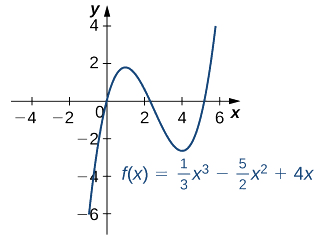
Kazi f (x) = (1/3) x ^ 3 - (5/2) x ^ 2 + 4x imewekwa. Kazi ina upeo wa ndani katika x = 1 na kiwango cha chini cha x = 4. — Kielelezo\(\PageIndex{5}\): Kazi hii ina upeo wa ndani na kiwango cha chini cha ndani.

b Kutumia utawala mnyororo, tunaona derivative ni

\(f'(x)=3(x^2−1)^2(2x)=6x(x^2−1)^2.\)

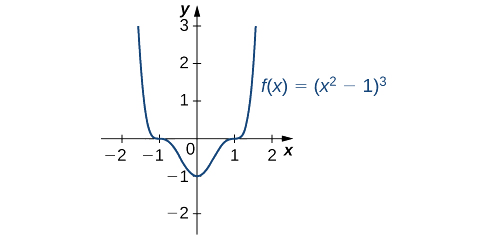
Kwa hiyo,\(f\) ina pointi muhimu wakati\(x=0\) na wakati\(x^2−1=0\). Tunahitimisha kuwa pointi muhimu ni\(x=0,±1\). Kutoka kwenye grafu ya\(f\) kwenye Kielelezo\(\PageIndex{6}\), tunaona kwamba\(f\) ina kiwango cha chini cha ndani (na kabisa)\(x=0\), lakini haina extremum ya ndani\(x=1\) au\(x=−1\).

Kazi f (x) = (x ^ 2 - 1) 3 imewekwa. Kazi ina kiwango cha chini cha ndani katika x = 0, na pointi za kupindua saa x = ± 1. — Kielelezo\(\PageIndex{6}\): Kazi hii ina pointi tatu muhimu:\(x=0\),\(x=1\), na\(x=−1\). Kazi ina kiwango cha chini cha ndani (na kabisa)\(x=0\), lakini haina extrema katika pointi nyingine mbili muhimu.

c Kwa utawala wa quotient, tunaona kwamba derivative ni

\(f'(x)=\frac{4(1+x^2)−4x(2x)}{(1+x^2)^2}=\frac{4−4x^2}{(1+x^2)^2}\).

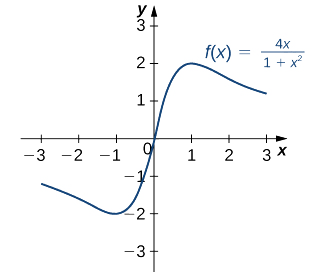
Derivative hufafanuliwa kila mahali. Kwa hiyo, tunahitaji tu kupata maadili kwa\(x\) wapi\(f'(x)=0\). Kutatua\(f'(x)=0\), tunaona kwamba ina\(4−4x^2=0,\) maana\(x=±1\). Kwa hiyo, pointi muhimu ni\(x=±1\). Kutoka grafu ya\(f\) katika Kielelezo\(\PageIndex{7}\), tunaona kwamba f ina kiwango cha juu kabisa katika\(x=1\) na kiwango cha chini kabisa katika\(x=−1.\) Hivyo,\(f\) ina upeo wa ndani katika\(x=1\) na kiwango cha chini ndani katika\(x=−1\). (Kumbuka kwamba kama\(f\) ina extremum kabisa juu ya muda\(I\) katika hatua\(c\) ambayo si mwisho wa\(I\), basi\(f\) ina extremum ndani katika\(c.)\)

Kazi f (x) = 4x/ (1 + x ^ 2) imewekwa. Kazi ina upeo wa ndani/kabisa saa x = 1 na kiwango cha chini cha ndani/kabisa saa x = -1. — Kielelezo\(\PageIndex{7}\): Kazi hii ina kiwango cha juu kabisa na kiwango cha chini kabisa.

Zoezi\(\PageIndex{1}\)

Kupata pointi zote muhimu kwa ajili ya\(f(x)=x^3−\frac{1}{2}x^2−2x+1.\)

Kidokezo: Tumia\(f'(x).\)

Jibu: \(x=\frac{−2}{3}, x=1\)

Kuweka Extrema Absolute

Theorem ya thamani uliokithiri inasema kuwa kazi inayoendelea juu ya muda uliofungwa, imefungwa ina kiwango cha juu kabisa na kiwango cha chini kabisa. Kama inavyoonekana katika Kielelezo\(\PageIndex{2}\), moja au yote ya extrema hizi kabisa inaweza kutokea katika endpoint. Ikiwa mwisho kabisa haufanyi mwishoni, hata hivyo, lazima ufanyike katika hatua ya mambo ya ndani, ambapo hali ya mwisho kabisa ni mwisho wa ndani. Kwa hiyo, kwa Theorem ya Fermat, hatua\(c\) ambayo extremum ya ndani hutokea lazima iwe hatua muhimu. Sisi muhtasari matokeo haya katika theorem ifuatayo.

Theorem\(\PageIndex{3}\): Location of Absolute Extrema

Hebu\(f\) iwe kazi inayoendelea juu ya muda uliofungwa, uliowekwa\(I\). Upeo kamili wa\(f\) juu\(I\) na kiwango cha chini kabisa cha\(f\) juu\(I\) lazima kutokea katika mwisho wa\(I\) au katika pointi muhimu ya\(f\) in\(I\).

Kwa wazo hili katika akili, hebu tuchunguze utaratibu wa kupata extrema kabisa.

Mkakati wa Kutatua Matatizo: Kuweka Extrema kabisa juu ya Muda uliofungwa

Fikiria kazi inayoendelea\(f\) inayoelezwa juu ya muda uliofungwa\([a,b].\)

Tathmini\(f\) katika endpoints\(x=a\) na\(x=b.\)
Pata pointi zote muhimu za uongo\(f\) huo juu ya muda\((a,b)\) na tathmini\(f\) katika pointi hizo muhimu.
Linganisha maadili yote yaliyopatikana katika (1) na (2). Kutoka “Eneo la Extrema Absolute,” extrema kabisa lazima kutokea katika mwisho au pointi muhimu. Kwa hiyo, ukubwa wa maadili haya ni kiwango cha juu kabisa cha\(f\). Kidogo cha maadili haya ni kiwango cha chini kabisa cha\(f\).

Sasa hebu tuangalie jinsi ya kutumia mkakati huu ili kupata kiwango cha juu kabisa na maadili ya chini kabisa kwa kazi zinazoendelea.

Mfano\(\PageIndex{2}\): Locating Absolute Extrema

Kwa kila moja ya kazi zifuatazo, pata kiwango cha juu kabisa na kiwango cha chini kabisa juu ya muda maalum na hali ambapo maadili hayo hutokea.

\(f(x)=−x^2+3x−2\)juu\([1,3].\)
\(f(x)=x^2−3x^{2/3}\)juu\([0,2]\).

Suluhisho

a Hatua ya 1. Tathmini\(f\) katika endpoints\(x=1\) na\(x=3\).

\(f(1)=0\)na\(f(3)=−2\)

Hatua ya 2. Tangu\(f'(x)=−2x+3, f'\) hufafanuliwa kwa namba zote halisi\(x.\) Kwa hiyo, hakuna pointi muhimu ambapo derivative haijulikani. Inabakia kuangalia wapi\(f'(x)=0\). Tangu\(f'(x)=−2x+3=0 \) saa\(x=\frac{3}{2}\) na\(\frac{3}{2}\) ni katika kipindi\([1,3], f(\frac{3}{2})\) ni mgombea wa extremum kabisa ya\(f\) juu\([1,3]\). Sisi kutathmini\(f(\frac{3}{2})\) na kupata

\(f\left(\frac{3}{2}\right)=\frac{1}{4}\).

Hatua ya 3. Tunaanzisha meza ifuatayo ili kulinganisha maadili yaliyopatikana katika hatua ya 1 na 2.

\(x\)	\(f(x)\)	Hitimisho
\(1\)	\(0\)
\(\frac{3}{2}\)	\(\frac{1}{4}\)	Kiwango cha juu kabisa
\(3\)	\(−2\)	Kima cha chini kabisa

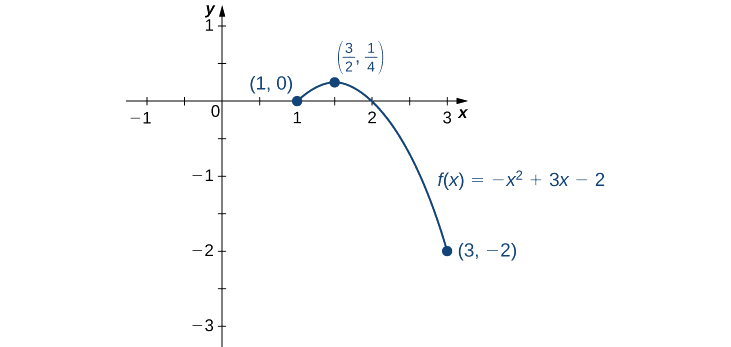
Kutoka meza, tunaona kwamba upeo kabisa wa\(f\) zaidi ya muda [1, 3] ni\(\frac{1}{4}\), na hutokea katika\(x=\frac{3}{2}\). kiwango cha chini kabisa ya\(f\) zaidi ya muda\([1, 3]\) ni\(−2\), na hutokea katika\(x=3\) kama inavyoonekana katika Kielelezo\(\PageIndex{8}\).

Kazi f (x) = - x ^ 2 + 3x - 2 imewekwa kutoka (1, 0) hadi (3, -1), na kiwango chake cha juu kilichowekwa alama (3/2, 1/4). — Kielelezo\(\PageIndex{8}\): Kazi hii ina kiwango cha juu kabisa na kiwango cha chini kabisa.

b Hatua ya 1. Tathmini\(f\) katika endpoints\(x=0\) na\(x=2\).

\(f(0)=0\)na\(f(2)=4−3\left(2\right)^{2/3}≈−0.762\)

Hatua ya 2. Derivative ya\(f\) hutolewa na

\(f'(x)=2x−\frac{2}{x^{1/3}}=\dfrac{2x^{4/3}−2}{x^{1/3}}\)

kwa\(x≠0\). Derivative ni sifuri wakati\(2x^{4/3}−2=0\), ambayo ina maana\(x=±1\). derivative ni undefined katika\(x=0\). Kwa hiyo, pointi muhimu ya\(f\) ni\(x=0,1,−1\). Hatua\(x=0\) ni mwisho, kwa hiyo tumekwisha tathmini\(f(0)\) katika hatua ya 1. Hatua\(x=−1\) sio wakati wa maslahi, kwa hiyo tunahitaji tu kutathmini\(f(1)\). Tunaona kwamba

\(f(1)=−2.\)

Hatua ya 3. Tunalinganisha maadili yaliyopatikana katika hatua ya 1 na 2, katika meza ifuatayo.

\(x\)	\(f(x)\)	Hitimisho
\(0\)	\(0\)	Kiwango cha juu kabisa
\(1\)	\(−2\)	Kima cha chini kabisa
\(2\)	\(−0.762\)

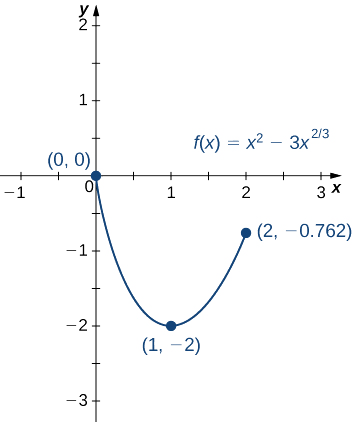
Tunahitimisha kuwa kiwango cha\(f\) juu kabisa cha muda\([0, 2]\) ni sifuri, na hutokea saa\(x=0\). kiwango cha chini kabisa ni\(−2,\) na hutokea katika\(x=1\) kama inavyoonekana katika Kielelezo\(\PageIndex{9}\).

Kazi f (x) = x ^ 2 - 3x^ (2/3) imewekwa kutoka (0, 0) hadi (2, -0.762), na kiwango cha chini chake kilichowekwa alama (1, -2). — Kielelezo\(\PageIndex{9}\): Kazi hii ina kiwango cha juu kabisa katika mwisho wa muda.

Zoezi\(\PageIndex{2}\)

Pata kiwango cha juu kabisa na kiwango cha chini kabisa cha\(f(x)=x^2−4x+3\) zaidi ya muda\([1,4]\).

Kidokezo: Angalia pointi muhimu. Tathmini\(f\) katika pointi zote muhimu na mwisho.

Jibu: Upeo kabisa ni\(3\) na hutokea\(x=4\). Kima cha chini kabisa ni\(−1\) na kinatokea\(x=2\).

Kwa hatua hii, tunajua jinsi ya kupata extrema kabisa kwa kazi zinazoendelea juu ya vipindi vilivyofungwa. Sisi pia defined extrema ndani na kuamua kwamba kama kazi\(f\) ina extremum ndani katika hatua\(c\), basi\(c\) lazima hatua muhimu ya\(f\). Hata hivyo,\(c\) kuwa hatua muhimu si hali ya kutosha\(f\) kwa kuwa na extremum ndani katika\(c\). Baadaye katika sura hii, sisi kuonyesha jinsi ya kuamua kama kazi kweli ina extremum mitaa katika hatua muhimu. Kwanza, hata hivyo, tunahitaji kuanzisha Theorem ya Theorem ya Maana, ambayo itasaidia tunapochambua tabia ya grafu ya kazi.

Dhana muhimu

Kazi inaweza kuwa na kiwango cha juu kabisa na kiwango cha chini kabisa, na moja tu ya mwisho kabisa, au hawana kiwango cha juu kabisa au kiwango cha chini kabisa.
Ikiwa kazi ina extremum ya ndani, hatua ambayo hutokea lazima iwe hatua muhimu. Hata hivyo, kazi haina haja ya kuwa na extremum ya ndani katika hatua muhimu.
Kazi inayoendelea juu ya muda uliofungwa, imefungwa ina kiwango cha juu kabisa na kiwango cha chini kabisa. Kila mwisho hutokea kwa hatua muhimu au mwisho.

faharasa

uliokithiri kabisa: ikiwa\(f\) ina kiwango cha juu kabisa au kiwango cha chini kabisa\(c\), tunasema\(f\) ina extremum kabisa\(c\)

kiwango cha juu kabisa: kama\(f(c)≥f(x)\) kwa wote\(x\) katika uwanja wa\(f\), tunasema\(f\) ina kiwango cha juu kabisa katika\(c\)

kiwango cha chini kabisa: kama\(f(c)≤f(x)\) kwa wote\(x\) katika uwanja wa\(f\), tunasema\(f\) ina kiwango cha chini kabisa katika\(c\)

hatua muhimu: kama\(f'(c)=0\) au\(f'(c)\) ni undefined, tunasema kwamba c ni hatua muhimu ya\(f\)

thamani uliokithiri theorem: ikiwa\(f\) ni kazi inayoendelea juu ya kipindi cha mwisho, kilichofungwa, basi\(f\) ina kiwango cha juu kabisa na kiwango cha chini kabisa

Theorem ya Fermat: kama\(f\) ina extremum ndani katika\(c\), basi\(c\) ni hatua muhimu ya\(f\)

uliokithiri wa ndani: kama\(f\) ina kiwango cha chini ndani au ndani katika\(c\), tunasema\(f\) ina extremum ndani katika\(c\)

upeo wa ndani: kama kuna muda\(I\) vile kwamba\(f(c)≥f(x)\) kwa ajili ya wote\(x∈I\), tunasema\(f\) ina kiwango cha juu ndani katika\(c\)

kiwango cha chini cha ndani: kama kuna muda\(I\) vile kwamba\(f(c)≤f(x)\) kwa ajili ya wote\(x∈I\), tunasema\(f\) ina kiwango cha chini ndani\(c\)