4.2: Makadirio ya mstari na Tofauti

Malengo ya kujifunza

• Eleza makadirio linear kwa kazi katika hatua.
• Andika mstari wa kazi iliyotolewa.
• Chora grafu inayoonyesha matumizi ya tofauti ili kukadiria mabadiliko kwa kiasi.
• Tumia makosa ya jamaa na makosa ya asilimia katika kutumia makadirio tofauti.

Tumeona tu jinsi derivatives kuruhusu sisi kulinganisha kiasi kuhusiana kwamba ni kubadilisha baada ya muda. Katika sehemu hii, tunachunguza matumizi mengine ya derivatives: uwezo wa takriban kazi ndani ya nchi na kazi za mstari. Kazi za mstari ni kazi rahisi ambazo zinafanya kazi, kwa hiyo hutoa chombo muhimu cha kukadiria maadili ya kazi. Aidha, mawazo yaliyowasilishwa katika sehemu hii ni ya jumla baadaye katika maandishi wakati sisi kujifunza jinsi ya takriban kazi na juu shahada polynomials Kuanzishwa kwa Power Series na Kazi.

Upimaji wa mstari wa Kazi katika Point

Fikiria kazi\(f\) ambayo ni tofauti katika hatua\(x=a\). Kumbuka kwamba mstari wa tangent kwenye grafu ya\(f\) saa\(a\) hutolewa na equation

\[y=f(a)+f'(a)(x−a). \nonumber \]

Kwa mfano, fikiria kazi\(f(x)=\frac{1}{x}\) katika\(a=2\). Tangu\(f\) ni differentiable katika\(x=2\) na\(f'(x)=−\frac{1}{x^2}\), tunaona kwamba\(f'(2)=−\frac{1}{4}\). Kwa hiyo, mstari wa tangent kwenye grafu ya\(f\) at\(a=2\) hutolewa na equation

\[y=\frac{1}{2}−\frac{1}{4}(x−2). \nonumber \]

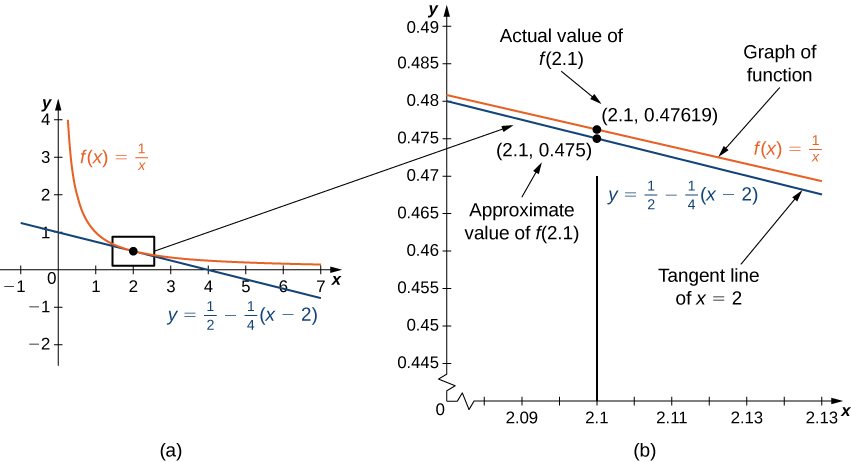
Kielelezo\(\PageIndex{1a}\) inaonyesha grafu ya\(f(x)=\frac{1}{x}\) pamoja na mstari tangent kwa\(f\) saa\(x=2\). Kumbuka kuwa kwa\(x\) karibu\(2\), grafu ya mstari wa tangent iko karibu na grafu ya\(f\). Matokeo yake, tunaweza kutumia equation ya mstari wa tangent ili takriban\(f(x)\) kwa\(x\) karibu\(2\). Kwa mfano, ikiwa\(x=2.1\),\(y\) thamani ya hatua inayofanana kwenye mstari wa tangent ni

\[y=\frac{1}{2}−\frac{1}{4}(2.1−2)=0.475. \nonumber \]

Thamani halisi ya\(f(2.1)\) hutolewa na

\[f(2.1)=\frac{1}{2.1}≈0.47619. \nonumber \]

Kwa hiyo, line tangent inatupa makadirio haki nzuri ya\(f(2.1)\) (Kielelezo\(\PageIndex{1b}\)). Hata hivyo, kumbuka kuwa kwa maadili ya\(x\) mbali na\(2\), equation ya mstari tangent haina kutupa makadirio nzuri. Kwa mfano, ikiwa\(x=10\),\(y\) thamani ya hatua inayofanana kwenye mstari wa tangent ni

\[y=\frac{1}{2}−\frac{1}{4}(10−2)=\frac{1}{2}−2=−1.5, \nonumber \]

ambapo thamani ya kazi katika\(x=10\) ni\(f(10)=0.1.\)

Kielelezo\(\PageIndex{1}\): (a) line tangent kwa\(f(x)=1/x\) saa\(x=2\) hutoa makadirio nzuri\(f\) kwa\(x\) karibu\(2\). (b) Katika\(x=2.1\), thamani ya\(y\) kwenye mstari wa tangent kwa\(f(x)=1/x\) ni\(0.475\). Thamani halisi ya\(f(2.1)\) ni\(1/2.1\), ambayo ni takriban\(0.47619\).

Kwa ujumla, kwa kazi tofauti\(f\), equation ya mstari wa tangent kwa\(f\) at\(x=a\) inaweza kutumika kwa takriban\(f(x)\) kwa\(x\) karibu\(a\). Kwa hiyo, tunaweza kuandika

\(f(x)≈f(a)+f'(a)(x−a)\)kwa\(x\) karibu\(a\).

Tunaita kazi ya mstari

\[L(x)=f(a)+f'(a)(x−a) \label{linearapprox} \]

linear makadirio, au tangent line makadirio, ya\(f\) saa\(x=a\). Kazi hii pia\(L\) inajulikana kama linearization ya\(f\) saa\(x=a.\)

Kuonyesha jinsi muhimu makadirio linear inaweza kuwa, sisi kuangalia jinsi ya kupata makadirio linear kwa\(f(x)=\sqrt{x}\) saa\(x=9.\)

Mfano\(\PageIndex{1}\): Linear Approximation of \(\sqrt{x}\)

Kupata linear makadirio ya\(f(x)=\sqrt{x}\) saa\(x=9\) na kutumia makadirio ya kukadiria\(\sqrt{9.1}\).

Suluhisho

Kwa kuwa sisi ni kuangalia kwa makadirio linear katika\(x=9,\) kutumia Equation\ ref {linearapprox} tunajua makadirio linear ni iliyotolewa na

\[L(x)=f(9)+f'(9)(x−9). \nonumber \]

Tunahitaji kupata\(f(9)\) na\(f'(9).\)

\(f(x)=\sqrt{x}⇒f(9)=\sqrt{9}=3\)

\(f'(x)=\frac{1}{2\sqrt{x}}⇒f'(9)=\frac{1}{2\sqrt{9}}=\frac{1}{6}\)

Kwa hiyo, makadirio ya mstari hutolewa na Kielelezo\(\PageIndex{2}\).

\[L(x)=3+\frac{1}{6}(x−9) \nonumber \]

Kutumia makadirio ya mstari, tunaweza kukadiria\(\sqrt{9.1}\) kwa kuandika

\[\sqrt{9.1}=f(9.1)≈L(9.1)=3+\frac{1}{6}(9.1−9)≈3.0167. \nonumber \]

Kielelezo\(\PageIndex{2}\): mitaa linear makadirio ya\(f(x)=\sqrt{x}\) saa\(x=9\) hutoa makadirio\(f\) ya kwa\(x\) karibu\(9\).

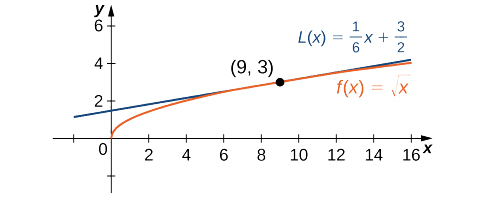
Uchambuzi

Kutumia calculator, thamani ya\(\sqrt{9.1}\) maeneo manne ya decimal ni\(3.0166\). thamani iliyotolewa na makadirio linear\(3.0167\),, ni karibu sana na thamani kupatikana kwa calculator, hivyo inaonekana kwamba kutumia makadirio hii linear ni njia nzuri ya kukadiria\(\sqrt{x}\), angalau kwa x karibu\(9\). Wakati huo huo, inaweza kuonekana isiyo ya kawaida kutumia makadirio linear wakati tunaweza tu kushinikiza vifungo chache kwenye calculator kutathmini\(\sqrt{9.1}\). Hata hivyo, calculator inatathminije\(\sqrt{9.1}\)? Calculator inatumia makadirio! Kwa kweli, calculators na kompyuta kutumia makadirio wakati wote kutathmini maneno ya hisabati; wao tu kutumia makadirio ya juu-shahada.

Zoezi\(\PageIndex{1}\)

Kupata mitaa linear makadirio ya\(f(x)=\sqrt[3]{x}\) saa\(x=8\). Tumia kwa takriban\(\sqrt[3]{8.1}\) maeneo tano ya decimal.

Kidokezo

\(L(x)=f(a)+f'(a)(x−a)\)

Jibu

\(L(x)=2+\frac{1}{12}(x−8);\)\(2.00833\)

Mfano\(\PageIndex{2}\): Linear Approximation of \(\sin x \)

Find makadirio linear ya\(f(x)=\sin x \) saa\(x=\frac{π}{3}\) na matumizi yake kwa takriban\(\sin(62°).\)

Suluhisho

Kwanza tunaona kwamba tangu\(\frac{π}{3}\) rad ni sawa na\(60°\), kutumia linear makadirio katika\(x=π/3\) inaonekana busara. Makadirio ya mstari hutolewa na

\(L(x)=f(\frac{π}{3})+f'(\frac{π}{3})(x−\frac{π}{3}).\)

Tunaona kwamba

\(f(x)=\sin x ⇒f(\frac{π}{3})=\sin(\frac{π}{3})=\frac{\sqrt{3}}{2}\)

\(f'(x)=\cos x ⇒f'(\frac{π}{3})=\cos(\frac{π}{3})=\frac{1}{2}\)

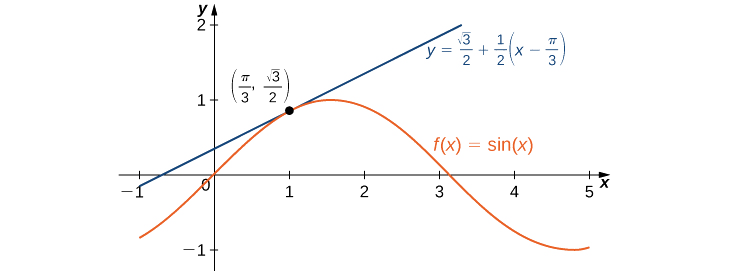
Kwa hiyo, makadirio ya mstari wa\(f\) saa\(x=π/3\) hutolewa na Kielelezo\(\PageIndex{3}\).

\(L(x)=\frac{\sqrt{3}}{2}+\frac{1}{2}(x−\frac{π}{3})\)

Ili kukadiria\(\sin(62°)\) kutumia\(L\), lazima kwanza tubadilishe\(62°\) kuwa radians. Tuna\(62°=\frac{62π}{180}\) radians, hivyo makadirio\(\sin(62°)\) ya hutolewa na

\(\sin(62°)=f(\frac{62π}{180})≈L(\frac{62π}{180})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{62π}{180}−\frac{π}{3})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{2π}{180})=\frac{\sqrt{3}}{2}+\frac{π}{180}≈0.88348.\)

Kielelezo\(\PageIndex{3}\): linear makadirio ya\(f(x)=\sin x \) saa\(x=π/3\) hutoa makadirio\(\sin x \) ya kwa\(x\) karibu\(π/3.\)

Zoezi\(\PageIndex{2}\)

Kupata makadirio linear kwa\(f(x)=\cos x \) saa\(x=\frac{π}{2}.\)

Kidokezo

\(L(x)=f(a)+f'(a)(x−a)\)

Jibu

\(L(x)=−x+\frac{π}{2}\)

Makadirio ya mstari inaweza kutumika katika kukadiria mizizi na nguvu. Katika mfano unaofuata, tunapata makadirio linear kwa\(f(x)=(1+x)^n\) saa\(x=0\), ambayo inaweza kutumika kukadiria mizizi na nguvu kwa idadi halisi karibu\(1\). Wazo lile linaweza kupanuliwa kwa kazi ya fomu\(f(x)=(m+x)^n\) ili kukadiria mizizi na nguvu karibu na idadi tofauti\(m\).

Mfano\(\PageIndex{3}\): Approximating Roots and Powers

Kupata linear makadirio ya\(f(x)=(1+x)^n\) saa\(x=0\). Tumia makadirio haya kukadiria\((1.01)^3.\)

Suluhisho

Makadirio ya mstari katika\(x=0\) hutolewa na

\(L(x)=f(0)+f'(0)(x−0).\)

Kwa sababu

\(f(x)=(1+x)^n⇒f(0)=1\)

\(f'(x)=n(1+x)^{n−1}⇒f'(0)=n,\)

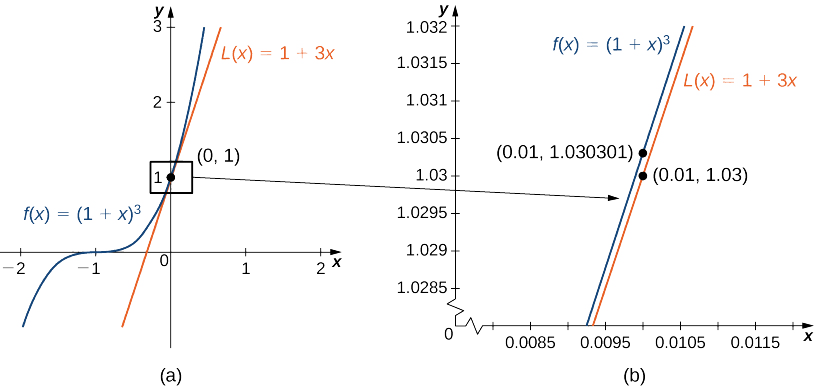
makadirio ya mstari hutolewa na Kielelezo\(\PageIndex{4a}\).

\(L(x)=1+n(x−0)=1+nx\)

Tunaweza takriban\((1.01)^3\) kwa kutathmini\(L(0.01)\) wakati\(n=3\). Sisi kuhitimisha kwamba

\((1.01)^3=f(1.01)≈L(1.01)=1+3(0.01)=1.03.\)

Kielelezo\(\PageIndex{4}\): (a) linear makadirio ya\(f(x)\) saa\(x=0\) ni\(L(x)\). (b) Thamani halisi ya\(1.01^3\) ni\(1.030301\). makadirio linear ya\(f(x)\)\(x=0\) makadirio\(1.01^3\) ya kuwa\(1.03\).

Zoezi\(\PageIndex{3}\)

Kupata makadirio linear ya\(f(x)=(1+x)^4\) saa\(x=0\) bila kutumia matokeo kutoka mfano uliopita.

Kidokezo

\(f'(x)=4(1+x)^3\)

Jibu

\(L(x)=1+4x\)

Tofauti

Tumeona kwamba makadirio linear inaweza kutumika kukadiria maadili kazi. Pia inaweza kutumika kukadiria kiasi kazi thamani mabadiliko kutokana na mabadiliko madogo katika pembejeo. Ili kujadili hili rasmi zaidi, tunafafanua dhana inayohusiana: tofauti. Tofauti hutupa njia ya kukadiria kiasi mabadiliko ya kazi kutokana na mabadiliko madogo katika maadili ya pembejeo.

Tulipoangalia kwanza derivatives, tulitumia nukuu ya Leibniz\(dy/dx\) kuwakilisha derivative ya kwa heshima\(y\) na\(x\). Ingawa tulitumia maneno\(dy\) na\(dx\) katika nukuu hii, hawakuwa na maana kwao wenyewe. Hapa tunaona maana ya maneno\(dy\) na\(dx\). Tuseme\(y=f(x)\) ni kazi tofauti. Hebu\(dx\) kuwa variable huru ambayo inaweza kupewa nambari yoyote isiyo ya zero halisi, na kufafanua kutofautiana tegemezi\(dy\) na

\[dy=f'(x)\,dx. \label{diffeq} \]

Ni muhimu kutambua kwamba\(dy\) ni kazi ya wote\(x\) na\(dx\). Maneno\(dy\) na\(dx\) huitwa tofauti. Tunaweza kugawanya pande zote mbili za Equation\ ref {differq}\(dx,\) ambayo mavuno

\[\frac{dy}{dx}=f'(x). \label{inteq} \]

Huu ndio maneno ya kawaida ambayo tumetumia kuashiria derivative. Equation\ ref {inteq} inajulikana kama aina tofauti ya Equation\ ref {differq}.

Mfano\(\PageIndex{4}\): Computing Differentials

Kwa kila moja ya kazi zifuatazo, tafuta\(dy\) na tathmini wakati\(x=3\) na\(dx=0.1.\)

1. \(y=x^2+2x\)
2. \(y=\cos x \)

Suluhisho

Hatua muhimu ni kuhesabu derivative. Wakati sisi kuwa na kwamba, tunaweza kupata\(dy\) moja kwa moja.

a. kwa kuwa\(f(x)=x^2+2x,\) tunajua\(f'(x)=2x+2\), na kwa hiyo

\(dy=(2x+2)\,dx.\)

Wakati\(x=3\) na\(dx=0.1,\)

\(dy=(2⋅3+2)(0.1)=0.8.\)

b Tangu\(f(x)=\cos x , f'(x)=−\sin(x).\) Hii inatupa

\(dy=−\sin x \,dx.\)

Wakati\(x=3\) na\(dx=0.1,\)

\(dy=−\sin(3)(0.1)=−0.1\sin(3).\)

Zoezi\(\PageIndex{4}\)

Kwa\(y=e^{x^2}\), kupata\(dy\).

Kidokezo

\(dy=f'(x)\,dx\)

Jibu

\(dy=2xe^{x^2}dx\)

Sasa tunaunganisha tofauti kwa makadirio ya mstari. Tofauti zinaweza kutumika kukadiria mabadiliko katika thamani ya kazi inayotokana na mabadiliko madogo katika maadili ya pembejeo. Fikiria kazi\(f\) ambayo ni tofauti katika hatua\(a\). Tuseme\(x\) mabadiliko ya pembejeo kwa kiasi kidogo. Tunavutiwa na kiasi gani\(y\) mabadiliko ya pato. Ikiwa\(x\) mabadiliko kutoka\(a\) kwa\(a+dx\), basi mabadiliko ndani\(x\) ni\(dx\) (pia\(Δx\) yameashiria), na mabadiliko\(y\) hutolewa na

\[Δy=f(a+dx)−f(a). \nonumber \]

Badala ya kuhesabu mabadiliko halisi katika\(y\), hata hivyo, mara nyingi ni rahisi kwa takriban mabadiliko katika\(y\) kwa kutumia makadirio linear. Kwa\(x\) karibu\(a, f(x)\) inaweza kuwa takriban na makadirio linear (Equation\ ref {linearapprox})

\[L(x)=f(a)+f'(a)(x−a). \nonumber \]

Kwa hiyo, kama\(dx\) ni ndogo,

\[f(a+dx)≈L(a+dx)=f(a)+f'(a)(a+dx−a). \nonumber \]

Hiyo ni,

\[f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx. \nonumber \]

Kwa maneno mengine, mabadiliko halisi katika kazi\(f\) kama\(x\) kuongezeka kutoka\(a\) kwa\(a+dx\) ni takriban tofauti kati ya\(L(a+dx)\) na\(f(a)\), wapi\(L(x)\) linear makadirio ya\(f\) saa\(a\). Kwa ufafanuzi wa\(L(x)\), tofauti hii ni sawa na\(f'(a)\,dx\). Kwa muhtasari,

\[Δy=f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx=dy. \nonumber \]

Kwa hiyo, tunaweza kutumia tofauti\(dy=f'(a)\,dx\) ili kukadiria mabadiliko katika\(y\) ikiwa\(x\) huongezeka kutoka\(x=a\) hadi\(x=a+dx\). Tunaweza kuona hii katika grafu ifuatayo.

Kielelezo\(\PageIndex{5}\):\(dy=f'(a)\,dx\) Tofauti hutumiwa kukadiria mabadiliko halisi\(y\) ikiwa\(x\) huongezeka kutoka\(a\) kwa\(a+dx\).

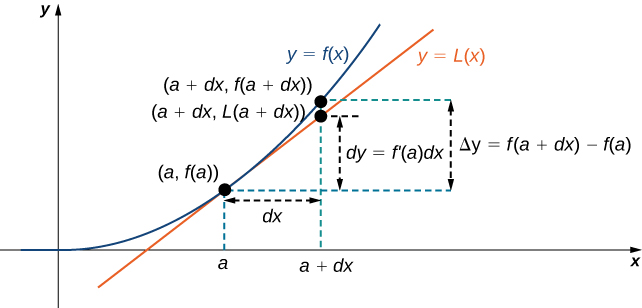
Sasa tunaangalia jinsi ya kutumia tofauti ili kukadiria mabadiliko katika thamani ya kazi inayotokana na mabadiliko madogo katika thamani ya pembejeo. Kumbuka hesabu na tofauti ni rahisi zaidi kuliko kuhesabu maadili halisi ya kazi na matokeo ni karibu sana na kile tunachopata kwa hesabu halisi zaidi.

Mfano\(\PageIndex{5}\): Approximating Change with Differentials

Hebu\(y=x^2+2x.\) Compute\(Δy\) na\(dy\) wakati\(x=3\) kama\(dx=0.1.\)

Suluhisho

Mabadiliko halisi katika\(y\) ikiwa\(x\) mabadiliko kutoka\(x=3\) kwa\(x=3.1\) yanatolewa na

\(Δy=f(3.1)−f(3)=[(3.1)^2+2(3.1)]−[3^2+2(3)]=0.81.\)

Mabadiliko ya takriban\(y\) yanatolewa na\(dy=f'(3)\,dx\). Tangu\(f'(x)=2x+2,\) tuna

\(dy=f'(3)\,dx=(2(3)+2)(0.1)=0.8.\)

Zoezi\(\PageIndex{5}\)

Kwa\(y=x^2+2x,\) kupata\(Δy\) na\(dy\) wakati\(x=3\) kama\(dx=0.2.\)

Kidokezo

\(dy=f'(3)\,dx, \;Δy=f(3.2)−f(3)\)

Jibu

\(dy=1.6, \; Δy=1.64\)

Kuhesabu Kiasi cha Hitilafu

Aina yoyote ya kipimo inakabiliwa na kiasi fulani cha kosa. Katika maombi mengi, kiasi fulani kinahesabiwa kulingana na vipimo. Kwa mfano, eneo la mduara linahesabiwa kwa kupima radius ya mduara. Hitilafu katika kipimo cha radius husababisha kosa katika thamani ya computed ya eneo hilo. Hapa tunachunguza aina hii ya hitilafu na kujifunza jinsi tofauti zinaweza kutumiwa kukadiria kosa.

Fikiria kazi\(f\) na pembejeo ambayo ni kiasi cha kipimo. Tuseme thamani halisi ya kiasi cha kipimo ni\(a\), lakini thamani ya kipimo ni\(a+dx\). Tunasema kosa la kipimo ni\(dx\) (au\(Δx\)). Matokeo yake, hitilafu hutokea kwa kiasi kilichohesabiwa\(f(x)\). Aina hii ya hitilafu inajulikana kama kosa lililoenezwa na hutolewa na

\[Δy=f(a+dx)−f(a). \nonumber \]

Kwa kuwa vipimo vyote vinaweza kukabiliwa na kiwango fulani cha hitilafu, hatujui thamani halisi ya kiasi kilichopimwa, kwa hiyo hatuwezi kuhesabu kosa lililoenezwa hasa. Hata hivyo, kutokana na makadirio ya usahihi wa kipimo, tunaweza kutumia tofauti ili takriban kosa lililoenezwa\(Δy.\) Hasa, ikiwa\(f\) ni kazi tofauti katika\(a\), kosa lililoenezwa ni

\[Δy≈dy=f'(a)\,dx. \nonumber \]

Kwa bahati mbaya, hatujui thamani halisi\(a.\) Hata hivyo, tunaweza kutumia thamani ya kipimo\(a+dx,\) na makadirio

\[Δy≈dy≈f'(a+dx)\,dx. \nonumber \]

Katika mfano unaofuata, tunaangalia jinsi tofauti zinaweza kutumiwa kukadiria kosa katika kuhesabu kiasi cha sanduku ikiwa tunadhani kipimo cha urefu wa upande kinafanywa kwa kiasi fulani cha usahihi.

Mfano\(\PageIndex{6}\): Volume of a Cube

Tuseme urefu wa upande wa mchemraba hupimwa kuwa\(5\) cm na usahihi wa\(0.1\) cm.

1. Tumia tofauti ili kukadiria hitilafu katika kiasi cha computed ya mchemraba.
2. Futa kiasi cha mchemraba ikiwa urefu wa upande ni (i)\(4.9\) cm na (ii)\(5.1\) cm ili kulinganisha hitilafu iliyokadiriwa na hitilafu halisi ya uwezo.

Suluhisho

a. kipimo cha urefu wa upande ni sahihi ndani ya\(±0.1\) cm. Kwa hiyo,

\(−0.1≤dx≤0.1.\)

Kiasi cha mchemraba hutolewa na\(V=x^3\), ambayo inaongoza

\(dV=3x^2dx.\)

Kutumia urefu wa urefu wa\(5\) cm, tunaweza kukadiria kwamba

\(−3(5)^2(0.1)≤dV≤3(5)^2(0.1).\)

Kwa hiyo,

\(−7.5≤dV≤7.5.\)

b Kama urefu upande ni kweli\(4.9\) cm, basi kiasi cha mchemraba ni

\(V(4.9)=(4.9)^3=117.649\text{cm}^3.\)

Ikiwa urefu wa upande ni kweli\(5.1\) cm, basi kiasi cha mchemraba ni

\(V(5.1)=(5.1)^3=132.651\text{cm}^3.\)

Kwa hiyo, kiasi halisi cha mchemraba ni kati\(117.649\) na\(132.651\). Kwa kuwa urefu wa upande unapimwa kuwa sentimita 5, kiasi cha computed ni\(V(5)=5^3=125.\) Kwa hiyo, kosa katika kiasi cha computed ni

\(117.649−125≤ΔV≤132.651−125.\)

Hiyo ni,

\(−7.351≤ΔV≤7.651.\)

Tunaona hitilafu inakadiriwa\(dV\) iko karibu na hitilafu halisi ya uwezo katika kiasi kilichohesabiwa.

Zoezi\(\PageIndex{6}\)

Tathmini kosa katika kiasi cha computed ya mchemraba ikiwa urefu wa upande unapimwa kuwa\(6\) cm na usahihi wa\(0.2\) cm.

Kidokezo

\(dV=3x^2dx\)

Jibu

Kipimo cha kiasi ni sahihi kwa ndani\(21.6\,\text{cm}^3\).

Hitilafu ya kipimo\(dx\ (=Δx)\) na hitilafu iliyoenezwa\(Δy\) ni makosa kabisa. Sisi ni kawaida nia ya ukubwa wa makosa jamaa na ukubwa wa wingi kuwa kipimo au mahesabu. Kutokana na makosa kabisa\(Δq\) kwa kiasi fulani, sisi kufafanua makosa jamaa kama\(\frac{Δq}{q}\), ambapo\(q\) ni thamani halisi ya wingi. Hitilafu ya asilimia ni kosa la jamaa lililoonyeshwa kama asilimia. Kwa mfano, ikiwa tunapima urefu wa ngazi kuwa\(63\) ndani. wakati urefu halisi ulipo., kosa kamili ni 1 katika. lakini kosa la jamaa ni\(\frac{1}{62}=0.016\), au\(1.6\%\).\(62\) Kwa kulinganisha, ikiwa tunapima upana wa kipande cha kadibodi kuwa\(8.25\) katika. wakati upana halisi ni\(8\)., kosa letu kabisa\(\frac{1}{4}\) liko., ambapo kosa la jamaa ni\(\frac{0.25}{8}=\frac{1}{32}\), au\(3.1\%.\) Kwa hiyo, kosa la asilimia katika kipimo cha kadi ni kubwa, hata ingawa\(0.25\) katika. ni chini\(1\) ya.

Mfano\(\PageIndex{7}\): Relative and Percentage Error

Mwanaanga kutumia kamera hupima radius ya Dunia kama\(4000\) mi na kosa la\(±80\) mi. Hebu tutumie tofauti ili kukadiria makosa ya jamaa na asilimia ya kutumia kipimo hiki cha radius kuhesabu kiasi cha Dunia, kwa kuzingatia sayari ni nyanja kamilifu.

Solution: Kama kipimo cha radius ni sahihi kwa ndani\(±80,\) tuna

\(−80≤dr≤80.\)

Tangu kiasi cha nyanja kinatolewa na\(V=(\frac{4}{3})πr^3,\) tuna

\(dV=4πr^2dr.\)

Kutumia radius kipimo cha\(4000\) mi, tunaweza kukadiria

\(−4π(4000)^2(80)≤dV≤4π(4000)^2(80).\)

Ili kukadiria kosa la jamaa, fikiria\(\dfrac{dV}{V}\). Kwa kuwa hatujui thamani halisi ya kiasi\(V\), tumia radius kipimo\(r=4000\) mi ili kukadiria\(V\). Tunapata\(V≈(\frac{4}{3})π(4000)^3\). Kwa hiyo, hitilafu ya jamaa inatimiza

\(\frac{−4π(4000)^2(80)}{4π(4000)^3/3}≤\dfrac{dV}{V}≤\frac{4π(4000)^2(80)}{4π(4000)^3/3},\)

ambayo simplifies kwa

\(−0.06≤\dfrac{dV}{V}≤0.06.\)

Hitilafu ya jamaa ni\(0.06\) na kosa la asilimia ni\(6\%\).

Zoezi\(\PageIndex{7}\)

Tambua kosa la asilimia ikiwa radius ya Dunia inapimwa kuwa\(3950\) mi na kosa la\(±100\) mi.

Kidokezo

Tumia ukweli kwamba\(dV=4πr^2dr\) kupata\(dV/V\).

Jibu

\(7.6\%\)

Dhana muhimu

• Kazi inayoweza kutofautishwa\(y=f(x)\) inaweza kuhesabiwa\(a\) na kazi ya mstari

\(L(x)=f(a)+f'(a)(x−a).\)

• Kwa kazi\(y=f(x)\), ikiwa\(x\) mabadiliko kutoka\(a\) kwa\(a+dx\), basi

\(dy=f'(x)\,dx\)

ni makadirio ya mabadiliko katika\(y\). Mabadiliko halisi katika\(y\) ni

\(Δy=f(a+dx)−f(a).\)

• Hitilafu ya kipimo\(dx\) inaweza kusababisha kosa kwa kiasi kilichohesabiwa\(f(x)\). Hitilafu katika kiasi kilichohesabiwa inajulikana kama kosa lililoenezwa. Hitilafu iliyoenezwa inaweza kuhesabiwa na

\(dy≈f'(x)\,dx.\)

• Ili kukadiria kosa la jamaa la kiasi fulani\(q\), tunakadiria\(\frac{Δq}{q}\).

Mlinganyo muhimu

• Ukadiriaji wa mstari

\(L(x)=f(a)+f'(a)(x−a)\)

• Tofauti

\(dy=f'(x)\,dx\)

faharasa

tofauti

tofauti\(dx\) ni tofauti ya kujitegemea ambayo inaweza kupewa nambari yoyote isiyo ya zero halisi; tofauti\(dy\) hufafanuliwa kuwa\(dy=f'(x)\,dx\)

fomu tofauti

kutokana na kazi\(y=f'(x),\) differentiable equation\(dy=f'(x)\,dx\) ni aina tofauti ya derivative ya kuhusiana\(y\) na\(x\)

makadirio ya mstari

kazi linear\(L(x)=f(a)+f'(a)(x−a)\) ni makadirio linear ya\(f\) saa\(x=a\)

kosa la asilimia

kosa la jamaa lililoonyeshwa kama asilimia

hitilafu iliyoenezwa

hitilafu ambayo husababisha kiasi kilichohesabiwa\(f(x)\) kutokana na kosa la kipimo\(dx\)

hitilafu ya jamaa

kutokana na hitilafu kabisa\(Δq\) kwa kiasi fulani,\(\frac{Δq}{q}\) ni kosa jamaa.

tangent line makadirio (linearization)

tangu makadirio linear ya\(f\) saa\(x=a\) hufafanuliwa kwa kutumia equation ya mstari tangent, linear makadirio ya\(f\) saa pia\(x=a\) inajulikana kama tangent line makadirio ya\(f\) saa\(x=a\)