4.1: Viwango vinavyohusiana

Last updated
Save as PDF

Page ID: 178862

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Express kubadilisha kiasi katika suala la derivatives.
Pata mahusiano kati ya derivatives katika tatizo lililopewa.
Tumia utawala wa mnyororo kupata kiwango cha mabadiliko ya kiasi kimoja kinachotegemea kiwango cha mabadiliko ya kiasi kingine.

Tumeona kwamba kwa kiasi ambacho kinabadilika baada ya muda, viwango ambavyo mabadiliko haya yanatolewa na derivatives. Ikiwa kiasi kiwili kinachohusiana kinabadilika kwa muda, viwango ambavyo mabadiliko ya kiasi yanahusiana. Kwa mfano, ikiwa puto inajazwa na hewa, radius yote ya puto na kiasi cha puto huongezeka. Katika sehemu hii, tunazingatia matatizo kadhaa ambayo kiasi mbili au zaidi kinachohusiana kinabadilika na tunasoma jinsi ya kuamua uhusiano kati ya viwango vya mabadiliko ya kiasi hiki.

Kuanzisha Matatizo yanayohusiana na Viwango

Katika maombi mengi ya ulimwengu halisi, kiasi kinachohusiana kinabadilika kwa heshima na wakati. Kwa mfano, kama tunaona mfano puto tena, tunaweza kusema kwamba kiwango cha mabadiliko katika kiasi$V$, ni kuhusiana na kiwango cha mabadiliko katika Radius,$r$. Katika kesi hiyo, sisi kusema kwamba$\frac{dV}{dt}$ na$\frac{dr}{dt}$ ni kuhusiana na viwango kwa sababu$V$ ni kuhusiana na$r$. Hapa tunasoma mifano kadhaa ya kiasi kinachohusiana ambacho kinabadilika kwa heshima na wakati na tunaangalia jinsi ya kuhesabu kiwango kimoja cha mabadiliko kutokana na kiwango kingine cha mabadiliko.

Mfano$\PageIndex{1}$: Inflating a Balloon

Puto ya spherical inajazwa na hewa kwa kiwango cha mara kwa mara cha$2\,\text{cm}^3\text{/sec}$ (Kielelezo$\PageIndex{1}$). Je, radius inaongezeka kwa kasi wakati radius ni$3$ cm?

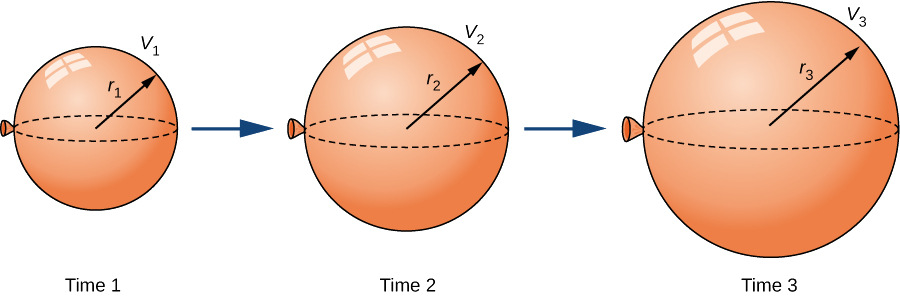
Balloons tatu zinaonyeshwa katika Times 1, 2, na 3. Balloons hizi huongezeka kwa kiasi na radius kama wakati unavyoongezeka. — Kielelezo$\PageIndex{1}$: Kama puto inajazwa na hewa, radius na kiasi huongezeka kwa heshima na wakati.

Suluhisho

Kiasi cha nyanja ya$r$ sentimita ya radius ni

$V=\frac{4}{3}πr^3\,\text{cm}^3.$

Tangu puto inajazwa na hewa, kiasi na radius ni kazi za wakati. Kwa hiyo,$t$ sekunde baada ya kuanza kujaza puto na hewa, kiasi cha hewa katika puto ni

$V(t)=\frac{4}{3}π\big[r(t)\big]^3\text{cm}^3.$

Kutofautisha pande zote mbili za equation hii kwa heshima na wakati na kutumia utawala wa mnyororo, tunaona kwamba kiwango cha mabadiliko katika kiasi kinahusiana na kiwango cha mabadiliko katika radius na equation

$V'(t)=4π\big[r(t)\big]^2r′(t).$

puto ni kujazwa na hewa kwa kiwango cha mara kwa mara ya$2 \,\text{cm}^3\text{/sec}$, hivyo$V'(t)=2\,\text{cm}^3\text{/sec}$. Kwa hiyo,

$2\,\text{cm}^3\text{/sec}=\Big(4π\big[r(t)\big]^2\;\text{cm}^2\Big)⋅\Big(r'(t)\;\text{cm/s}\Big),$

ambayo ina maana

$r'(t)=\dfrac{1}{2π\big[r(t)\big]^2}\;\text{cm/sec}$.

Wakati$r=3$ cm radius,

$r'(t)=\dfrac{1}{18π}\;\text{cm/sec}.$

Zoezi$\PageIndex{1}$

Je, ni kiwango cha haraka cha mabadiliko ya radius wakati$r=6$ cm?

Kidokezo: $\dfrac{dr}{dt}=\dfrac{1}{2πr^2}$

Jibu: $\frac{1}{72π}$cm/sec, au takriban 0.0044 cm/sec

Kabla ya kuangalia mifano mingine, hebu tufafanue mkakati wa kutatua matatizo tutakayotumia kutatua matatizo yanayohusiana na viwango.

Mkakati wa Kutatua Matatizo: Kutatua Tatizo la Viwango vya Kuhusiana

Weka alama kwa vigezo vyote vinavyohusika katika tatizo. Chora takwimu ikiwa inatumika.
Hali, katika suala la vigezo, taarifa kwamba ni kutolewa na kiwango cha kuamua.
Kupata equation zinazohusiana vigezo kuletwa katika hatua ya 1.
Kutumia utawala wa mnyororo, kutofautisha pande zote mbili za equation zilizopatikana katika hatua ya 3 kuhusiana na kutofautiana kwa kujitegemea. Equation hii mpya itahusisha derivatives.
Badilisha maadili yote inayojulikana katika equation kutoka hatua ya 4, kisha kutatua kwa kiwango haijulikani ya mabadiliko

Kumbuka kwamba wakati wa kutatua tatizo linalohusiana na viwango, ni muhimu sio kubadilisha maadili inayojulikana hivi karibuni. Kwa mfano, ikiwa thamani ya kiasi cha kubadilisha inabadilishwa kuwa equation kabla ya pande zote mbili za equation zifafanuliwa, basi kiasi hicho kitatenda kama mara kwa mara na derivative yake haitaonekana katika equation mpya iliyopatikana katika hatua ya 4. Tunachunguza kosa hili la uwezo katika mfano unaofuata.

Mifano ya Mchakato

Hebu sasa kutekeleza mkakati tu ilivyoelezwa kutatua matatizo kadhaa kuhusiana viwango. Mfano wa kwanza unahusisha ndege ya kuruka juu. Uhusiano tunayojifunza ni kati ya kasi ya ndege na kiwango ambacho umbali kati ya ndege na mtu ardhini unabadilika.

Mfano$\PageIndex{2}$: An Airplane Flying at a Constant Elevation

Ndege inaruka juu ya mwinuko wa mara kwa mara wa$4000$ ft. Mtu anaangalia ndege kutoka msimamo$3000$ ft kutoka chini ya mnara wa redio. Ndege inaruka kwa usawa mbali na mtu huyo. Ikiwa ndege inaruka kwa kiwango cha$600$ ft/sec, kwa kiwango gani umbali kati ya mtu na ndege huongezeka wakati ndege inapita juu ya mnara wa redio?

Suluhisho

Hatua ya 1. Chora picha, kuanzisha vigezo kuwakilisha kiasi tofauti kushiriki.

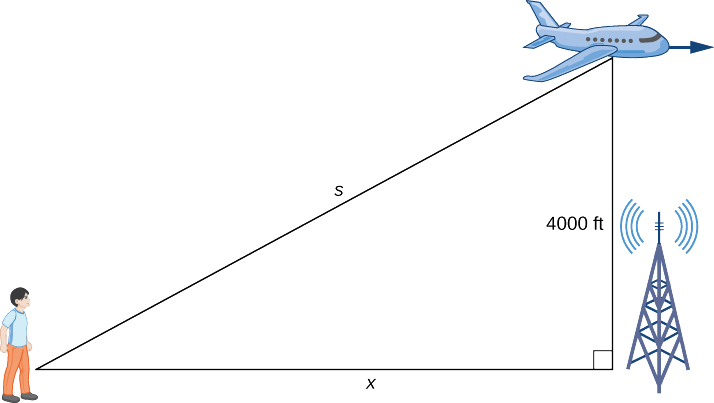
Pembetatu ya kulia inafanywa na mtu chini, ndege katika hewa, na mnara wa redio kwenye pembe ya kulia chini. Hypotenuse ni s, umbali juu ya ardhi kati ya mtu na mnara wa redio ni x, na upande kinyume na mtu (yaani, urefu kutoka ardhini hadi ndege) ni 4000 ft. — Kielelezo$\PageIndex{2}$: Ndege inaruka kwa urefu wa mara kwa mara wa$4000$ ft. Umbali kati ya mtu na ndege na mtu na mahali ardhini moja kwa moja chini ya ndege hubadilika. Tunaashiria kiasi hicho na vigezo$s$ na$x$, kwa mtiririko huo.

Kama inavyoonekana,$x$ inaashiria umbali kati ya mtu na msimamo chini moja kwa moja chini ya ndege. Variable$s$ inaashiria umbali kati ya mtu na ndege. Kumbuka kwamba wote wawili$x$ na$s$ ni kazi za wakati. Hatuwezi kuanzisha variable kwa urefu wa ndege kwa sababu inabaki katika mwinuko wa mara kwa mara wa$4000$ ft. Kwa kuwa urefu wa kitu juu ya ardhi hupimwa kama umbali mfupi kati ya kitu na ardhi, sehemu ya mstari wa urefu wa 4000 ft ni perpendicular kwa sehemu ya mstari wa$x$ miguu ya urefu, na kujenga pembetatu sahihi.

Hatua ya 2. Kwa kuwa$x$ inaashiria umbali usawa kati ya mtu na uhakika chini ya ndege,$dx/dt$ inawakilisha kasi ya ndege. Tunaambiwa kasi ya ndege ni$600$ ft/sec. Kwa hiyo,$\frac{dx}{dt}=600$ ft/sec. Kwa kuwa tunaulizwa kupata kiwango cha mabadiliko katika umbali kati ya mtu na ndege wakati ndege iko moja kwa moja juu ya mnara wa redio, tunahitaji kupata$ds/dt$ wakati$x=3000$ ft.

Hatua ya 3. Kutoka kwa takwimu, tunaweza kutumia theorem ya Pythagorean kuandika equation inayohusiana$x$ na$s$:

$[x(t)]^2+4000^2=[s(t)]^2.$

Hatua ya 4. Kutofautisha equation hii kwa heshima na wakati na kutumia ukweli kwamba derivative ya mara kwa mara ni sifuri, sisi kufika equation

\[x\frac{dx}{dt}=s\frac{ds}{dt}.\nonumber \]

Hatua ya 5. Pata kiwango ambacho umbali kati ya mtu na ndege unaongezeka wakati ndege iko moja kwa moja juu ya mnara wa redio. Hiyo ni, kupata$\frac{ds}{dt}$ wakati$x=3000$ ft. Kwa kuwa kasi ya ndege ni$600$ ft/sec, tunajua kwamba$\frac{dx}{dt}=600$ ft/sec. Sisi si kupewa thamani wazi kwa$s$; Hata hivyo, tangu sisi ni kujaribu kupata$\frac{ds}{dt}$ wakati$x=3000$ ft, tunaweza kutumia theorem Pythagorean kuamua umbali$s$ wakati$x=3000$ ft na urefu ni$4000$ ft. Kutatua equation

$3000^2+4000^2=s^2$

kwa$s$, tuna$s=5000$ ft wakati wa riba. Kutumia maadili haya, tunahitimisha kuwa$ds/dt$

ni suluhisho la equation

$(3000)(600)=(5000)⋅\dfrac{ds}{dt}$.

Kwa hiyo,

$\dfrac{ds}{dt}=\dfrac{3000⋅600}{5000}=360\,\text{ft/sec}.$

Kumbuka: Wakati wa kutatua matatizo yanayohusiana na viwango, ni muhimu sio kubadilisha maadili kwa vigezo hivi karibuni. Kwa mfano, katika hatua ya 3, sisi kuhusiana kiasi kutofautiana$x(t)$ na$s(t)$ kwa equation

$[x(t)]^2+4000^2=[s(t)]^2.$

Kwa kuwa ndege inabakia urefu wa mara kwa mara, si lazima kuanzisha kutofautiana kwa urefu, na tunaruhusiwa kutumia mara kwa mara 4000 ili kutaja kiasi hicho. Hata hivyo, kiasi kingine mbili kinabadilika. Kama sisi kimakosa kubadilishwa$x(t)=3000$ katika equation kabla ya kutofautisha, equation yetu ingekuwa

$3000^2+4000^2=[s(t)]^2.$

Baada ya kutofautisha, equation yetu itakuwa

$0=s(t)\dfrac{ds}{dt}.$

Matokeo yake, tunataka kimakosa kuhitimisha kwamba$\frac{ds}{dt}=0.$

Zoezi$\PageIndex{2}$

Je! Kasi ya ndege ni nini ikiwa umbali kati ya mtu na ndege unaongezeka kwa kiwango cha$300$ ft/sec?

Kidokezo: $\dfrac{ds}{dt}=300$ft/sec

Jibu: $500$ft/sec

Sasa tunarudi tatizo linalohusisha uzinduzi wa roketi tangu mwanzo wa sura.

Mfano$\PageIndex{3}$: Chapter Opener - A Rocket Launch

Roketi imezinduliwa ili iweze kuongezeka kwa wima. Kamera imewekwa$5000$ ft kutoka pedi ya uzinduzi. Wakati roketi iko juu$1000$ ya pedi ya uzinduzi, kasi yake ni$600$ ft/sec.

Picha ya roketi kuinua mbali. — Kielelezo$\PageIndex{3}$: (mikopo: mabadiliko ya kazi na Steve Jurvetson, Wikimedia Commons)

Kupata kiwango muhimu ya mabadiliko ya angle kamera kama kazi ya muda ili anakaa kulenga roketi.

Suluhisho

Hatua ya 1. Chora picha kuanzisha vigezo.

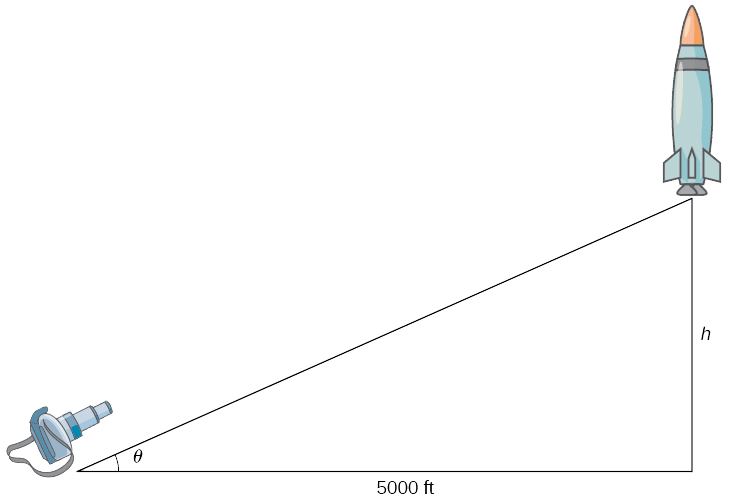
Pembetatu ya kulia inaundwa na kamera kwenye moja ya pembe zisizo za kulia na roketi kwenye pembe nyingine isiyo ya haki. Pembe na kamera ina kipimo. Umbali kutoka roketi hadi ardhini ni h; kumbuka kuwa hii ni upande kinyume na angle na kipimo ρ. Upande ulio karibu na angle na kipimo ni 5000 ft. — Kielelezo$\PageIndex{4}$: kamera ni nafasi nzuri$5000$ ft kutoka pedi uzinduzi wa roketi. Urefu wa roketi na angle ya kamera hubadilika kwa heshima na wakati. Tunaashiria kiasi hicho na vigezo$h$ na$θ$, kwa mtiririko huo.

Hebu$h$ kuashiria urefu wa roketi juu ya pedi uzinduzi na$θ$ kuwa angle kati ya lens kamera na ardhi.

Hatua ya 2. Sisi ni kujaribu kupata kiwango cha mabadiliko katika angle ya kamera kwa heshima na wakati ambapo roketi ni 1000 ft mbali ya ardhi. Hiyo ni, tunahitaji kupata$\frac{dθ}{dt}$ wakati$h=1000$ ft. Wakati huo, tunajua kasi ya roketi ni$\frac{dh}{dt}=600$ ft/sec.

Hatua ya 3. Sasa tunahitaji kupata equation zinazohusiana na kiasi mbili kwamba ni kubadilisha kwa heshima na wakati:$h$ na$θ$. Tunawezaje kuunda equation kama hiyo? Kutumia ukweli kwamba tumejenga pembetatu sahihi, ni kawaida kufikiri juu ya kazi za trigonometric. Kumbuka kwamba$\tan θ$ ni uwiano wa urefu wa upande wa pili wa pembetatu hadi urefu wa upande wa karibu. Hivyo, tuna

$\tan θ=\dfrac{h}{5000}$.

Hii inatupa equation

$h=5000\tan θ.$

Hatua ya 4. Kutofautisha equation hii kwa heshima na wakati$t$, tunapata

$\dfrac{dh}{dt}=5000\sec^2θ\dfrac{dθ}{dt}$.

Hatua ya 5. Tunataka kupata$\frac{dθ}{dt}$ wakati$h=1000$ ft. Kwa wakati huu, tunajua kwamba$\frac{dh}{dt}=600$ ft/sec. Tunahitaji kuamua$\sec^2θ$. Kumbuka kwamba$\sec θ$ ni uwiano wa urefu wa hypotenuse hadi urefu wa upande wa karibu. Tunajua urefu wa upande wa karibu ni$5000$ ft. Kuamua urefu wa hypotenuse, tunatumia theorem ya Pythagorean, ambapo urefu wa mguu mmoja ni$5000$ ft, urefu wa mguu mwingine ni$h=1000$ ft, na urefu wa hypotenuse ni$c$ miguu kama inavyoonekana katika takwimu zifuatazo.

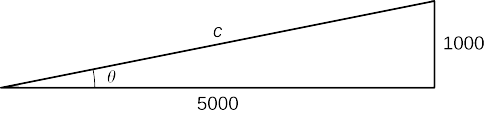
$Pembetatu ya kulia ina angle moja na kipimo. Hypotenuse ni c, urefu wa upande kinyume na angle na kipimo ni 1000, na upande karibu na angle na kipimo ni 5000.$

Tunaona kwamba

$1000^2+5000^2=c^2$

na sisi kuhitimisha kwamba hypotenuse ni

$c=1000\sqrt{26}\,\text{ft}.$

Kwa hiyo, wakati$h=1000,$ tuna

$\sec^2θ=\left(\dfrac{1000\sqrt{26}}{5000}\right)^2=\dfrac{26}{25}.$

Kumbuka kutoka hatua ya 4 kwamba equation$\frac{dθ}{dt}$ zinazohusiana na maadili yetu inayojulikana ni

$\dfrac{dh}{dt}=5000\sec^2θ\dfrac{dθ}{dt}.$

Wakati$h=1000$ ft, tunajua kwamba$\frac{dh}{dt}=600$ ft/sec na$\sec^2θ=\frac{26}{25}$. Kubadilisha maadili haya katika equation uliopita, tunawasili kwenye equation

$600=5000\left(\frac{26}{25}\right)\dfrac{dθ}{dt}$.

Kwa hiyo,$\dfrac{dθ}{dt}=\dfrac{3}{26}$ rad/sec.

Zoezi$\PageIndex{3}$

Kiwango gani cha mabadiliko ni muhimu kwa angle ya mwinuko wa kamera ikiwa kamera imewekwa chini kwa umbali wa$4000$ ft kutoka pedi ya uzinduzi na kasi ya roketi ni$500$ ft/sec wakati roketi iko$2000$ ft mbali ya ardhi?

Kidokezo: Kupata$\frac{dθ}{dt}$ wakati$h=2000$ ft. Wakati huo,$\frac{dh}{dt}=500$ ft/sec.

Jibu: $\frac{1}{10}$rad/sec

Katika mfano unaofuata, tunazingatia maji yanayotokana na funnel yenye umbo la koni. Tunalinganisha kiwango ambacho kiwango cha maji katika koni kinapungua kwa kiwango ambacho kiasi cha maji kinapungua.

Mfano$\PageIndex{4}$: Water Draining from a Funnel

Maji ni kukimbia kutoka chini ya funnel koni umbo kwa kiwango cha$0.03\,\text{ft}^3\text{/sec}$. Urefu wa funnel ni$2$ ft na radius juu ya funnel ni$1$ ft. Kwa kiwango gani urefu wa maji katika funnel hubadilika wakati urefu wa maji ni$\frac{1}{2}$ ft?

Suluhisho

Hatua ya 1: Chora picha kuanzisha vigezo.

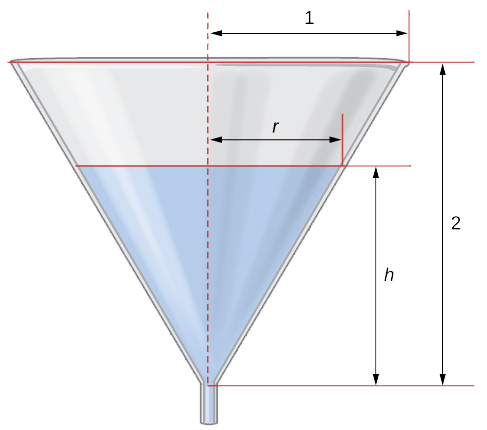
Funnel inavyoonyeshwa kwa urefu wa 2 na radius 1 juu yake. Funnel ina maji kwa urefu h, wakati ambapo radius ni r. — Kielelezo$\PageIndex{5}$: Maji yanatoka kwenye funnel ya urefu$2$ ft na radius$1$ ft. Urefu wa maji na radius ya maji hubadilika kwa muda. Tunaashiria kiasi hiki na vigezo$h$ na$r$, kwa mtiririko huo.

Hebu$h$ kuashiria urefu wa maji katika funnel, au kuashiria radius ya maji kwenye uso wake, na$V$ kuashiria kiasi cha maji.

Hatua ya 2: Tunahitaji kuamua$\frac{dh}{dt}$ wakati$h=\frac{1}{2}$ ft. Tunajua kwamba$\frac{dV}{dt}=−0.03$ ft/sec.

Hatua ya 3: Kiasi cha maji katika koni ni

$V=\frac{1}{3}πr^2h.$

Kutoka kwenye takwimu, tunaona kwamba tuna pembetatu sawa. Kwa hiyo, uwiano wa pande katika pembetatu mbili ni sawa. Kwa hiyo,$\frac{r}{h}=\frac{1}{2}$ au$r=\frac{h}{2}.$ Kutumia ukweli huu, equation kwa kiasi inaweza kuwa rahisi

$V=\frac{1}{3}π\left(\frac{h}{2}\right)^2h=\frac{π}{12}h^3$.

Hatua ya 4: Kutumia utawala wa mnyororo wakati wa kutofautisha pande zote mbili za equation hii kwa heshima na wakati$t$, tunapata

\[\frac{dV}{dt}=\frac{π}{4}h^2\frac{dh}{dt}.\nonumber \]

Hatua ya 5: Tunataka kupata$\frac{dh}{dt}$ wakati$h=\frac{1}{2}$ ft. Kwa kuwa maji ni kuondoka kwa kiwango cha$0.03\,\text{ft}^3\text{/sec}$, tunajua kwamba$\frac{dV}{dt}=−0.03\,\text{ft}^3\text{/sec}$. Kwa hiyo,

\[−0.03=\frac{π}{4}\left(\frac{1}{2}\right)^2\dfrac{dh}{dt},\nonumber \]

ambayo ina maana

\[−0.03=\frac{π}{16}\dfrac{dh}{dt}.\nonumber \]

Inafuata kwamba

\[\dfrac{dh}{dt}=−\frac{0.48}{π}=−0.153\,\text{ft/sec}.\nonumber \]

Zoezi$\PageIndex{4}$

Kwa kiwango gani urefu wa maji hubadilika wakati urefu wa maji ni$\frac{1}{4}$ ft?

Kidokezo: Tunahitaji kupata$\frac{dh}{dt}$ wakati$h=\frac{1}{4}.$

Jibu: $−0.61$ft/sec

Dhana muhimu

Ili kutatua tatizo la viwango vinavyohusiana, kwanza futa picha inayoeleza uhusiano kati ya kiasi mbili au zaidi zinazohusiana ambazo zinabadilika kwa heshima na wakati.
Kwa upande wa kiasi, sema habari iliyotolewa na kiwango cha kupatikana.
Kupata equation zinazohusiana kiasi.
Tumia upambanuzi, ukitumia utawala wa mnyororo kama inavyohitajika, ili kupata equation inayohusiana na viwango.
Hakikisha usiingie kiasi cha kutofautiana kwa moja ya vigezo mpaka baada ya kupata equation inayohusiana na viwango.

faharasa

viwango vinavyohusiana: ni viwango vya mabadiliko yanayohusiana na kiasi mbili au zaidi kuhusiana kwamba ni kubadilisha baada ya muda

Mfano\(\PageIndex{1}\): Inflating a Balloon

Zoezi\(\PageIndex{1}\)

Mkakati wa Kutatua Matatizo: Kutatua Tatizo la Viwango vya Kuhusiana

Mfano\(\PageIndex{2}\): An Airplane Flying at a Constant Elevation

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{3}\): Chapter Opener - A Rocket Launch

Zoezi\(\PageIndex{3}\)

Mfano\(\PageIndex{4}\): Water Draining from a Funnel

Zoezi\(\PageIndex{4}\)