Skip to main content
Global

3.10: Mazoezi ya Mapitio ya Sura ya 3

  1. Last updated
  2. Save as PDF
  • Page ID
    178903

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Sura ya Mapitio ya mazoezi

    Kweli au Uongo? Thibitisha jibu kwa ushahidi au mfano wa kukabiliana.

    1) Kila kazi ina derivative.

    Jibu
    Uongo

    2) Kazi inayoendelea ina derivative inayoendelea.

    3) Kazi inayoendelea ina derivative.

    Jibu
    Uongo

    4) Ikiwa kazi inatofautiana, inaendelea.

    Katika mazoezi ya 5 na 6, tumia ufafanuzi wa kikomo wa derivative ili kutathmini hasa derivative.

    5)\(f(x)=\sqrt{x+4}\)

    Jibu
    \(f'(x) = \dfrac{1}{2\sqrt{x+4}}\)

    6)\(f(x)=\dfrac{3}{x}\)

    Katika mazoezi ya 7 - 15, pata derivatives ya kazi zilizopewa.

    7)\(f(x)=3x^3−\dfrac{4}{x^2}\)

    Jibu
    \(f'(x) = 9x^2+\frac{8}{x^3}\)

    9)\(f(x)=(4−x^2)^3\)

    10)\(f(x)=e^{\sin x}\)

    Jibu
    \(f'(x) = e^{\sin x}\cos x\)

    11)\(f(x)=\ln(x+2)\)

    12)\(f(x)=x^2\cos x+x\tan x\)

    Jibu
    \(f'(x) = x\sec^2 x+2x\cos x+\tan x−x^2\sin x \)

    13)\(f(x)=\sqrt{3x^2+2}\)

    14)\(f(x)=\dfrac{x}{4}\sin^{−1}(x)\)

    Jibu
    \(f'(x) = \frac{1}{4}\left(\frac{x}{\sqrt{1−x^2}}+\sin^{−1} x\right)\)

    15)\(x^2y=(y+2)+xy\sin x\)

    Katika mazoezi 16 - 18, tafuta derivatives iliyoonyeshwa ya amri mbalimbali.

    16) derivative ya kwanza ya\(y=x(\ln x)\cos x\)

    Jibu
    \(\dfrac{dy}{dx} = \cos x⋅(\ln x+1)−x(\ln x)\sin x\)

    17) Derivative ya tatu ya\(y=(3x+2)^2\)

    18) Pili derivative ya\(y=4^x+x^2\sin x\)

    Jibu
    \(\dfrac{d^2y}{dx^2} = 4^x(\ln 4)^2+2\sin x+4x\cos x−x^2\sin x\)

    Katika mazoezi ya 19 na 20, pata equation ya mstari wa tangent kwa equations zifuatazo katika hatua maalum.

    19)\(y=\cos^{−1}(x)+x\) katika\(x=0\)

    20)\(y=x+e^x−\dfrac{1}{x}\) katika\(x=1\)

    Jibu
    \(y = (2+e)x−2\)

    Katika mazoezi 21 na 22, futa derivative ya kazi na grafu zilizopewa.

    21)

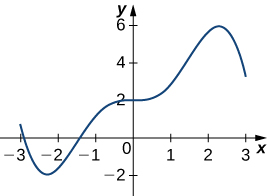
    Kazi huanza saa (-3, 0.5) na inapungua kwa kiwango cha chini cha mitaa saa (-2.3, -1). Kisha kazi huongezeka kupitia (-1.5, 0) na hupunguza ongezeko lake kupitia (0, 2). Kisha polepole huongezeka kwa kiwango cha juu cha ndani (2.3, 6) kabla ya kupungua kwa (3, 3).

    22)

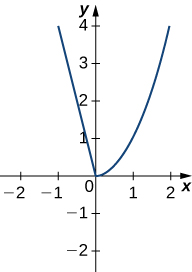
    Kazi hupungua kwa mstari kutoka (-1, 4) hadi asili, ambapo huongezeka kama x ^ 2, kupitia (1, 1) na (2, 4).

    Jibu
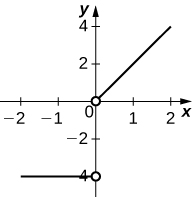
    Kazi ni mstari wa moja kwa moja y = -4 mpaka x = 0, ambapo inakuwa mstari wa moja kwa moja kuanzia mwanzo na mteremko 2. Hakuna thamani kwa ajili ya kazi hii katika x = 0.

    Maswali 22 na 23 yanahusu kiwango cha maji katika Ocean City, New Jersey, mwezi wa Januari, ambayo inaweza kuhesabiwa na\(w(t)=1.9+2.9\cos(\frac{π}{6}t),\) wapi\(t\) hupimwa kwa masaa baada ya usiku wa manane, na urefu hupimwa kwa miguu.

    22) Pata na graph derivative. Nini maana ya kimwili?

    23) Pata\(w′(3).\) Nini maana ya kimwili ya thamani hii?

    Jibu
    \(w′(3)=−\frac{2.9π}{6}\). Saa 3 asubuhi wimbi linapungua kwa kiwango cha 1.514 ft/hr.

    Maswali 24 na 25 yanazingatia kasi ya upepo ya Hurricane Katrina, ambayo iliathiri New Orleans, Louisiana, mwezi Agosti 2005. Data huonyeshwa kwenye meza.

    Masaa baada ya Midnight, Agosti Kasi ya upepo (mph)
    1 45
    5 75
    11 100
    29 115
    49 145
    58 175
    73 155
    81 125
    85 95
    107 35

    Upepo kasi ya Hurricane KatrinaSource: news.nationalgeographic.com/n... _timeline.html.

    24) Kutumia meza, tathmini ya derivative ya kasi ya upepo saa 39. Nini maana ya kimwili?

    25) Tathmini ya derivative ya kasi ya upepo saa 83. Nini maana ya kimwili?

    Jibu
    \(−7.5.\)Kasi ya upepo inapungua kwa kiwango cha 7.5 mph/hr