3.9: Derivatives ya Kazi za Kielelezo na Logarithmic

Malengo ya kujifunza

• Pata derivative ya kazi za kielelezo.
• Pata derivative ya kazi za logarithmic.
• Tumia tofauti ya logarithmic kuamua derivative ya kazi.

Hadi sasa, tumejifunza jinsi ya kutofautisha kazi mbalimbali, ikiwa ni pamoja na trigonometric, inverse, na kazi thabiti. Katika sehemu hii, sisi kuchunguza derivatives ya kazi kielelezo na logarithmic. Kama tulivyojadiliwa katika Utangulizi wa Kazi na Grafu, kazi za kielelezo zina jukumu muhimu katika kuimarisha ukuaji wa idadi ya watu na kuoza kwa vifaa vya mionzi. Kazi za Logarithmic zinaweza kusaidia kurejesha kiasi kikubwa na husaidia hasa kwa kuandika upya maneno ngumu.

Derivative ya Kazi ya Kielelezo

Kama vile tulipopata derivatives ya kazi nyingine, tunaweza kupata derivatives ya kazi za kielelezo na logarithmic kwa kutumia formula. Tunapoendeleza kanuni hizi, tunahitaji kufanya mawazo fulani ya msingi. Ushahidi ambao mawazo haya yanashikilia ni zaidi ya upeo wa kozi hii.

Kwanza kabisa, tunaanza na dhana kwamba kazi\(B(x)=b^x,\, b>0,\) inaelezwa kwa kila nambari halisi na inaendelea. Katika kozi ya awali, maadili ya kazi kielelezo kwa idadi zote za busara zilielezwa-kuanzia na ufafanuzi wa\(b^n\), ambapo\(n\) ni integer chanya - kama bidhaa ya\(b\) kuzidisha kwa yenyewe\(n\) mara. Baadaye, sisi defined\(b^0=1,b^{−n}=\dfrac{1}{b^n}\), kwa integer chanya\(n\), na\(b^{s/t}=(\sqrt[t]{b})^s\) kwa integers chanya\(s\) na\(t\). Ufafanuzi huu huacha wazi swali la thamani ya\(b^r\) wapi\(r\) namba halisi ya kiholela. Kwa kuchukua mwendelezo wa\(B(x)=b^x,b>0\), tunaweza kutafsiri\(b^r\) kama\(\displaystyle \lim_{x→r}b^x\) ambapo maadili ya\(x\) kama sisi kuchukua kikomo ni busara. Kwa mfano, tunaweza kuona\(4^π\) kama idadi ya kuridhisha

\[4^3<4^π<4^4,\quad 4^{3.1}<4^π<4^{3.2},\quad 4^{3.14}<4^π<4^{3.15}, \nonumber \]

\[4^{3.141}<4^{π}<4^{3.142},\quad 4^{3.1415}<4^{π}<4^{3.1416},\quad …. \nonumber \]

Kama tunavyoona katika meza ifuatayo,\(4^π≈77.88.\)

\(x\)	\(4^x\)	\(x\)	\(4^x\)
\ (x\)” style="text-align:katikati; ">\(4^3\)	\ (4^x\)” style="Nakala-align:katikati; "> 64	\ (x\)” style="text-align:katikati; ">\(4^{3.141593}\)	\ (4^x\)” style="Nakala-align:katikati; "> 77.8802710486
\ (x\)” style="text-align:katikati; ">\(4^{3.1}\)	\ (4^x\)” style="Nakala-align:katikati; "> 73.5166947198	\ (x\)” style="text-align:katikati; ">\(4^{3.1416}\)	\ (4^x\)” style="Nakala-align:katikati; "> 77.8810268071
\ (x\)” style="text-align:katikati; ">\(4^{3.14}\)	\ (4^x\)” style="Nakala-align:katikati; "> 77.7084726013	\ (x\)” style="text-align:katikati; ">\(4^{3.142}\)	\ (4^x\)” style="Nakala-align:katikati; "> 77.9242251944
\ (x\)” style="text-align:katikati; ">\(4^{3.141}\)	\ (4^x\)” style="Nakala-align:katikati; "> 77.8162741237	\ (x\)” style="text-align:katikati; ">\(4^{3.15}\)	\ (4^x\)” style="Nakala-align:katikati; "> 78.7932424541
\ (x\)” style="text-align:katikati; ">\(4^{3.1415}\)	\ (4^x\)” style="Nakala-align:katikati; "> 77.8702309526	\ (x\)” style="text-align:katikati; ">\(4^{3.2}\)	\ (4^x\)” style="Nakala-align:katikati; "> 84.4485062895
\ (x\)” style="text-align:katikati; ">\(4^{3.14159}\)	\ (4^x\)” style="Nakala-align:katikati; "> 77.8799471543	\ (x\)” style="text-align:katikati; ">\(4^{4}\)	\ (4^x\)” style="Nakala-align:katikati; "> 256

Inakadiriwa Thamani ya\(4^π\)

Sisi pia kudhani kwamba kwa\(B(x)=b^x,\, b>0\), thamani\(B′(0)\) ya derivative ipo. Katika sehemu hii, tunaonyesha kwamba kwa kufanya dhana hii ya ziada, inawezekana kuthibitisha kwamba kazi hiyo\(B(x)\) inatofautiana kila mahali.

Tunafanya dhana moja ya mwisho: kwamba kuna thamani ya kipekee\(b>0\) ya ambayo\(B′(0)=1\). Sisi kufafanua e kuwa thamani hii ya kipekee, kama tulivyofanya katika Utangulizi wa Kazi na Grafu. Kielelezo\(\PageIndex{1}\) hutoa grafu ya kazi\(y=2^x, \,y=3^x, \,y=2.7^x,\) na\(y=2.8^x\). Makadirio ya kuona ya mteremko wa mistari ya tangent kwa kazi hizi saa 0 hutoa ushahidi kwamba thamani ya e iko mahali fulani kati ya 2.7 na 2.8. Kazi\(E(x)=e^x\) inaitwa kazi ya asili ya kielelezo. Inverse yake,\(L(x)=\log_e x=\ln x\) inaitwa kazi ya asili ya logarithmic.

Kielelezo\(\PageIndex{1}\): Grafu ya\(E(x)=e^x\) ni kati\(y=2^x\) na\(y=3^x\).

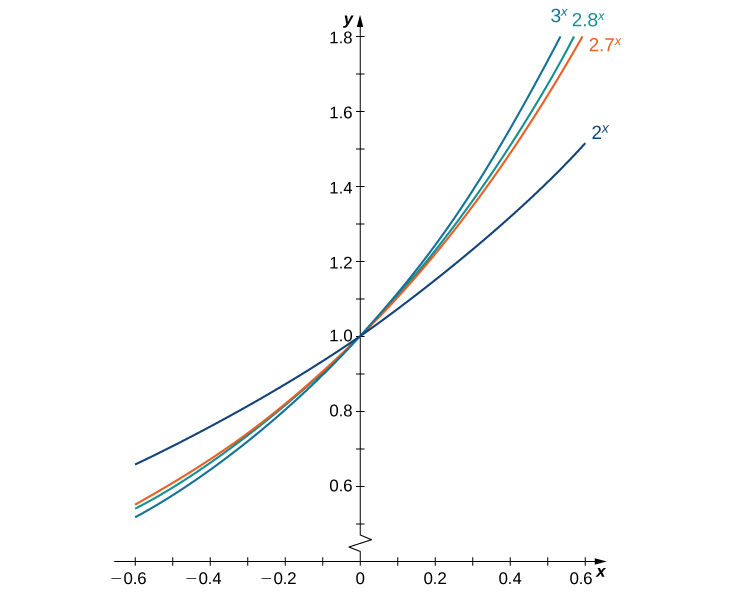
Kwa makadirio bora ya\(e\), tunaweza kujenga meza ya makadirio ya\(B′(0)\) kwa ajili ya kazi ya fomu\(B(x)=b^x\). Kabla ya kufanya hivyo, kumbuka kwamba

\[B′(0)=\lim_{x→0}\frac{b^x−b^0}{x−0}=\lim_{x→0}\frac{b^x−1}{x}≈\frac{b^x−1}{x} \nonumber \]

kwa maadili ya karibu\(x\) sana na sifuri. Kwa makadirio yetu, tunachagua\(x=0.00001\) na\(x=−0.00001\)

ili kupata makadirio

\[\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}. \nonumber \]

Angalia meza ifuatayo.

Jedwali: Kukadiria thamani ya\(e\)

\(b\)	\(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\)	\(b\)	\(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\)
\ (b\)” style="text-align:katikati; "> 2	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.693145<B′(0)<0.69315\)	\ (b\)” style="Nakala-align:katikati; "> 2.7183	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.000002<B′(0)<1.000012\)
\ (b\)” style="text-align:katikati; "> 2.7	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.993247<B′(0)<0.993257\)	\ (b\)” style="Nakala-align:katikati; "> 2.719	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.000259<B′(0)<1.000269\)
\ (b\)” style="Nakala-align:katikati; "> 2.71	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.996944<B′(0)<0.996954\)	\ (b\)” style="Nakala-align:katikati; "> 2.72	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.000627<B′(0)<1.000637\)
\ (b\)” style="Nakala-align:katikati; "> 2.718	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.999891<B′(0)<0.999901\)	\ (b\)” style="text-align:katikati; "> 2.8	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.029614<B′(0)<1.029625\)
\ (b\)” style="Nakala-align:katikati; "> 2.7182	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(0.999965<B′(0)<0.999975\)	\ (b\)” style="text-align:katikati; "> 3	\ (\ frac {b^ {-0.00001} -1} {-0.00001} <B( 0) <\ frac {b^ {0.00001} −1} {0.00001}.\)” style="text-align:center; ">\(1.098606<B′(0)<1.098618\)

Ushahidi kutoka meza unaonyesha kwamba\(2.7182<e<2.7183.\)

Grafu ya\(E(x)=e^x\) pamoja na mstari\(y=x+1\) inavyoonekana kwenye Kielelezo\(\PageIndex{2}\). Mstari huu ni tangent kwa grafu ya\(E(x)=e^x\) saa\(x=0\).

Kielelezo\(\PageIndex{2}\): Mstari wa tangent kwa\(E(x)=e^x\) saa\(x=0\) una mteremko 1.

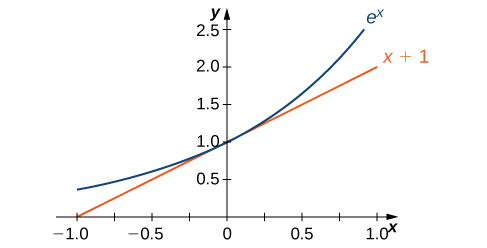
Sasa kwa kuwa tumeweka mawazo yetu ya msingi, tunaanza uchunguzi wetu kwa kuchunguza derivative ya\(B(x)=b^x, \,b>0\). Kumbuka kwamba tuna kudhani kwamba\(B′(0)\) ipo. Kwa kutumia ufafanuzi kikomo kwa derivative sisi kuhitimisha kwamba

\[B′(0)=\lim_{h→0}\frac{b^{0+h}−b^0}{h}=\lim_{h→0}\frac{b^h−1}{h} \nonumber \]

Kugeuka\(B′(x)\), tunapata zifuatazo.

\ (\ displaystyle\ kuanza {align*} B (x) &=\ lim_ {h → 0}\ frac {b ^ {x+h} -b ^ x} {h} &\ maandishi {Tumia ufafanuzi wa kikomo wa derivative.}\\ [4pt]
&=\ lim_ {h → 0}\ frac {b ^ xb ^ b ^ x} {h} {h ^ xb ^ x} {h} & &\ maandishi {Kumbuka kuwa} b ^ {x+h} =b ^ xb ^ h.\\ [4pt]
&=\ lim_ {h → 0}\ frac {b ^ x (b ^ h-1)} {h} &\ Nakala {Factor nje} b ^ x.\\ [4pt]
&=b ^ x\ lim_ {h → 0}\ frac {b ^ h-1} {h} & &\ maandishi {Weka mali ya mipaka.}\\ [4pt]
&=B ^ XB( 0) &\ maandishi {Matumizi} B( 0) =\ lim_ {h → 0}\ frac {b ^ {0+h} -b^0} {h} =\ lim_ {h→ 0}\ frac {b ^ h-1} {h}. \ mwisho {align*}\)

Tunaona kwamba kwa misingi ya dhana ambayo\(B(x)=b^x\) ni tofauti katika\(0,B(x)\) si tu kutofautisha kila mahali, lakini derivative yake ni

\[B′(x)=b^xB′(0).\nonumber \]

Kwa\(E(x)=e^x, \,E′(0)=1.\) hivyo, tuna\(E′(x)=e^x\). (Thamani\(B′(0)\) ya kazi ya kiholela ya fomu\(B(x)=b^x, \,b>0,\) itatokana baadaye.)

Derivative ya Kazi ya Kielelezo ya asili

Hebu\(E(x)=e^x\) kuwa kazi ya kielelezo ya asili. Kisha

\[E′(x)=e^x. \nonumber \]

Kwa ujumla,

\[\frac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x) \nonumber \]

Mfano\(\PageIndex{1}\): Derivative of an Exponential Function

Kupata derivative ya\(f(x)=e^{\tan(2x)}\).

Suluhisho:

Kutumia formula ya derivative na utawala wa mnyororo,

\[f′(x)=e^{\tan(2x)}\frac{d}{dx}\Big(\tan(2x)\Big)=e^{\tan(2x)}\sec^2(2x)⋅2 \nonumber \]

Mfano\(\PageIndex{2}\): Combining Differentiation Rules

Kupata derivative ya\(y=\dfrac{e^{x^2}}{x}\).

Suluhisho

Tumia derivative ya kazi ya asili ya kielelezo, utawala wa quotient, na utawala wa mnyororo.

\ (kuanza {align*} y&=\ dfrac {(e^ {x^2} 2) xx—1e^ {x^2}} {x^2} &\ maandishi {Tumia utawala wa quotient.}\\ [4pt]
&=\ dfrac {e ^ {x^2} (2x^2,11)} {x^2}} {x^2}} {x^2}} {x^2}} {x^2}} {x^2}} {x^2}} {x ^ 2}} {x^2}} {x^2}} {x^2} & &\ Nakala {Kurahisisha.} \ mwisho {align*}\)

Zoezi\(\PageIndex{1}\)

Kupata derivative ya\(h(x)=xe^{2x}\).

Kidokezo

Usisahau kutumia utawala wa bidhaa.

Jibu

\(h′(x)=e^{2x}+2xe^{2x}\)

Mfano\(\PageIndex{3}\): Applying the Natural Exponential Function

Koloni ya mbu ina idadi ya awali ya 1000. Baada ya\(t\) siku, idadi ya watu hutolewa na\(A(t)=1000e^{0.3t}\). Onyesha kwamba uwiano wa kiwango cha mabadiliko ya idadi ya watu\(A′(t)\), kwa idadi ya watu,\(A(t)\) ni mara kwa mara.

Suluhisho

Pata kwanza\(A′(t)\). Kwa kutumia utawala wa mnyororo, tuna\(A′(t)=300e^{0.3t}.\) Hivyo, uwiano wa kiwango cha mabadiliko ya idadi ya watu kwa idadi ya watu hutolewa na

\[\frac{A′(t)}{A(t)}=\frac{300e^{0.3t}}{1000e^{0.3t}}=0.3. \nonumber \]

Uwiano wa kiwango cha mabadiliko ya idadi ya watu kwa idadi ya watu ni mara kwa mara 0.3.

Zoezi\(\PageIndex{2}\)

Ikiwa\(A(t)=1000e^{0.3t}\) inaelezea idadi ya mbu baada ya\(t\) siku, kama ilivyo katika mfano uliopita, ni kiwango gani cha mabadiliko ya\(A(t)\) baada ya siku 4?

Kidokezo

Kupata\(A′(4)\).

Jibu

\(996\)

Derivative ya Kazi ya Logarithmic

Sasa kwa kuwa tuna derivative ya kazi ya kielelezo ya asili, tunaweza kutumia tofauti thabiti ili kupata derivative ya inverse yake, kazi ya asili ya logarithmic.

Ufafanuzi: Derivative ya Kazi ya asili ya Logarithmic

Kama\(x>0\) na\(y=\ln x\), basi

\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]

Kwa ujumla, hebu\(g(x)\) iwe kazi tofauti. Kwa maadili yote ambayo\(g′(x)>0\), derivative ya\(h(x)=\ln(g(x))\) hutolewa na\(x\)

\[h′(x)=\frac{1}{g(x)}g′(x). \nonumber \]

Ushahidi

Ikiwa\(x>0\) na\(y=\ln x\), kisha\(e^y=x.\) kutofautisha pande zote mbili za matokeo ya equation hii katika equation

\[e^y\frac{dy}{dx}=1. \nonumber \]

Kutatua kwa\(\dfrac{dy}{dx}\) mavuno

\[\frac{dy}{dx}=\frac{1}{e^y}. \nonumber \]

Hatimaye, sisi badala\(x=e^y\) ya kupata

\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]

Tunaweza pia hupata matokeo haya kwa kutumia theorem ya kazi ya inverse, kama ifuatavyo. Tangu\(y=g(x)=\ln x\)

ni inverse ya\(f(x)=e^x\), kwa kutumia kazi inverse theorem tuna

\[\frac{dy}{dx}=\frac{1}{f′(g(x))}=\frac{1}{e^{\ln x}}=\frac{1}{x}. \nonumber \]

Kutumia matokeo haya na kutumia utawala wa mnyororo ili\(h(x)=\ln(g(x))\) mavuno

\[h′(x)=\frac{1}{g(x)}g′(x). \label{lnder} \]

□

Grafu ya\(y=\ln x\) na derivative yake\(\dfrac{dy}{dx}=\dfrac{1}{x}\) inavyoonekana katika Kielelezo\(\PageIndex{3}\).

Kielelezo\(\PageIndex{3}\): Kazi\(y=\ln x\) inaongezeka\((0,+∞)\). Derivative yake\(y'=\frac{1}{x}\) ni kubwa kuliko sifuri juu\((0,+∞)\)

Mfano\(\PageIndex{4}\): Taking a Derivative of a Natural Logarithm

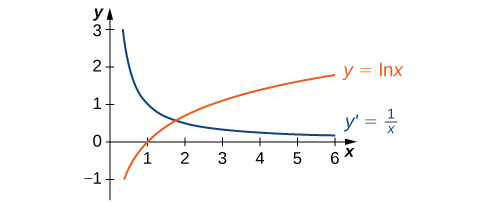
Kupata derivative ya\(f(x)=\ln(x^3+3x−4)\).

Suluhisho

Matumizi Equation\ ref {lnder} moja kwa moja.

\ (\ kuanza {align*} f′ (x) &=\ dfrac {1} {x ^ 3+3x-4}}} (3x^2+3) & &\ maandishi {Matumizi} g (x) =x ^ 3+3x-4\ maandishi {katika} h =\ dfrac {1} {g (x)} g′ (x).\\ [4 pt]
&=\ dfrac {3x^2+3} {x^3+3x-4} & &\ maandishi {Andika upya.} \ mwisho {align*}\)

Mfano\(\PageIndex{5}\): Using Properties of Logarithms in a Derivative

Kupata derivative ya\(f(x)=\ln\left(\dfrac{x^2\sin x}{2x+1}\right)\).

Suluhisho

Kwa mtazamo wa kwanza, kuchukua derivative hii inaonekana badala ngumu. Hata hivyo, kwa kutumia mali ya logarithms kabla ya kupata derivative, tunaweza kufanya tatizo rahisi zaidi.

\ (\ kuanza {align*} f (x) &=\ ln\ kushoto (\ frac {x ^ 2\ sin x} {2x+1}\ haki) =2\ ln x+\ ln (\ sin x) -\ ln (2x+1) &\ maandishi {Tumia mali ya logarithms.}\\ [4pt]
f′ (x) &=\ dfrac {2} x {2} x {} +\ kitanda x-\ dfrac {2} {2x+1} & &\ maandishi {Weka utawala wa jumla na} h( x) =\ dfrac {1} {g (x)} g( x). \ mwisho {align*}\)

Zoezi\(\PageIndex{3}\)

Tofautisha:\(f(x)=\ln(3x+2)^5\).

Kidokezo

Tumia mali ya logarithms ili kurahisisha kabla ya kuchukua derivative.

Jibu

\(f′(x)=\dfrac{15}{3x+2}\)

Sasa kwa kuwa tunaweza kutofautisha kazi ya asili ya logarithmic, tunaweza kutumia matokeo haya ili kupata derivatives ya\(y=\log_b x\) na\(y=b^x\) kwa\(b>0, \,b≠1\).

Derivatives ya Kazi za Kielelezo na za Logarithmic

Hebu\(b>0,b≠1,\) na hebu\(g(x)\) iwe kazi tofauti.

i. kama\(y=\log_b x\), basi

\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]

Kwa ujumla, ikiwa\(h(x)=\log_b(g(x))\), basi kwa maadili yote ambayo\(g(x)>0\),\(x\)

\[h′(x)=\frac{g′(x)}{g(x)\ln b}. \label{genlogder} \]

ii. Kama\(y=b^x,\) basi

\[\frac{dy}{dx}=b^x\ln b. \nonumber \]

Zaidi kwa ujumla, kama\(h(x)=b^{g(x)},\) basi

\[h′(x)=b^{g(x)}g'(x)\ln b \label{genexpder} \]

Ushahidi

Ikiwa\(y=\log_b x,\) basi\(b^y=x.\) Inafuata hiyo\(\ln(b^y)=\ln x\). Hivyo\(y\ln b=\ln x\). Kutatua kwa\(y\), tuna\(y=\dfrac{\ln x}{\ln b}\). Kutofautisha na kukumbuka kwamba\(\ln b\) ni mara kwa mara, tunaona kwamba

\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]

derivative katika Equation\ ref {genlogder} sasa ifuatavyo kutoka utawala mnyororo.

Kama\(y=b^x\). kisha\(\ln y=x\ln b.\) Kutumia tofauti thabiti, tena kuweka katika akili kwamba\(\ln b\) ni mara kwa mara, inafuata kwamba\(\dfrac{1}{y}\dfrac{dy}{dx}=\ln b\). Kutatua\(\dfrac{dy}{dx}\) na kubadilisha\(y=b^x\), tunaona kwamba

\[\frac{dy}{dx}=y\ln b=b^x\ln b. \nonumber \]

Derivative zaidi ya jumla (Equation\ ref {genexpder}) ifuatavyo kutoka utawala mnyororo.

□

Mfano\(\PageIndex{6}\): Applying Derivative Formulas

Kupata derivative ya\(h(x)=\dfrac{3^x}{3^x+2}\).

Suluhisho

Tumia utawala wa quotient na Kumbuka.

\ (\ kuanza {align*} h (x) &=\ dfrac {3 ^ x\ ln 3 (3 ^ x+2) -3^x\ ln 3 (3^x)} {(3^x+2) ^2} &\ maandishi {Tumia utawala wa quotient.}\\ [4pt]
&=\ dfrac {23^x\ ln 3} {(3x3 ^ x\ ln 3} {(3xpt) +2) ^2} & &\ maandishi {Kurahisisha.} \ mwisho {align*}\)

Mfano\(\PageIndex{7}\): Finding the Slope of a Tangent Line

Pata mteremko wa mstari wa tangent kwenye grafu ya\(y=\log_2 (3x+1)\) saa\(x=1\).

Suluhisho

Ili kupata mteremko, lazima tathmini\(\dfrac{dy}{dx}\) saa\(x=1\). Kutumia Equation\ ref {genlogder}, tunaona kwamba

\[\frac{dy}{dx}=\frac{3}{(3x+1)\ln 2}. \nonumber \]

Kwa kutathmini derivative katika\(x=1\), tunaona kwamba line tangent ina mteremko

\[\frac{dy}{dx}\bigg{|}_{x=1}=\frac{3}{4\ln 2}=\frac{3}{\ln 16}. \nonumber \]

Zoezi\(\PageIndex{4}\)

Kupata mteremko kwa tangent line kwa\(y=3^x\) saa\(x=2.\)

Kidokezo

Tathmini derivative katika\(x=2.\)

Jibu

\(9\ln(3)\)

Tofauti ya Logarithmic

Kwa hatua hii, tunaweza kuchukua derivatives ya kazi za fomu\(y=(g(x))^n\) kwa maadili fulani ya\(n\), pamoja na kazi za fomu\(y=b^{g(x)}\), wapi\(b>0\) na\(b≠1\). Kwa bahati mbaya, hatujui derivatives ya kazi kama vile\(y=x^x\) au\(y=x^π\). Kazi hizi zinahitaji mbinu inayoitwa upambanuzi wa logarithmic, ambayo inatuwezesha kutofautisha kazi yoyote ya fomu\(h(x)=g(x)^{f(x)}\). Pia inaweza kutumika kubadili tatizo tata sana tofauti katika moja rahisi, kama vile kutafuta derivative ya\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\). Tunaelezea mbinu hii katika mkakati wafuatayo wa kutatua matatizo.

Mkakati wa Kutatua matatizo: Kutumia Tofauti ya Logarithmic

1. Ili kutofautisha\(y=h(x)\) kutumia tofauti ya logarithmic, chukua logarithm ya asili ya pande zote mbili za equation ili kupata\(\ln y=\ln(h(x)).\)
2. Tumia mali ya logarithms kupanua\(\ln(h(x))\) iwezekanavyo.
3. Tofautisha pande zote mbili za equation. Kwenye kushoto tutakuwa na\(\dfrac{1}{y}\dfrac{dy}{dx}\).
4. Kuzidisha pande zote mbili za equation na\(y\) kutatua kwa\(\dfrac{dy}{dx}\).
5. Badilisha nafasi\(y\) na\(h(x)\).

Mfano\(\PageIndex{8}\): Using Logarithmic Differentiation

Kupata derivative ya\(y=(2x^4+1)^{\tan x}\).

Suluhisho

Tumia tofauti ya logarithmic ili kupata derivative hii.

\ (\ kuanza {align*}\ ln y&=\ ln (2x^ 4+1) ^ {\ tan x} & &\ maandishi {Hatua ya 1. Chukua logarithm ya asili ya pande zote mbili.}\\ [4pt]
\ ln y&=\ tan x\ ln (2x^ 4+1) & &\ maandishi {Hatua ya 2. Panua kutumia mali ya logarithms.}\\ [4pt]
\ dfrac {1} {y}\ dfrac {dfrac {dy} {dx} &=\ sec ^ 2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1}}\ tan x & &\ maandishi {Hatua ya 3. Tofautisha pande zote mbili. Tumia utawala wa bidhaa upande wa kulia.}\\ [4pt]
\ dfrac {dy} {dx} &=y(\ sec ^ 2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1}}}\ tan x) & &\ maandishi {Hatua ya 4. Kuzidisha kwa} y\ maandishi {pande zote mbili.}\\ [4pt]
\ dfrac {dy} {dx} & =( 2x^4+1) ^ {\ tan x} (\ sec ^ 2 x\ ln (2x^4+1) +\ dfrac {8x^3} {2x^4+1}}\ tan x) & &\ maandishi {Hatua ya 5. Mbadala} y= (2x^ 4+1) ^ {\ tan x}. \ mwisho {align*}\)

Mfano\(\PageIndex{9}\): Extending the Power Rule

Kupata derivative ya\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\).

Suluhisho

Tatizo hili linatumia mali ya logarithms na sheria za upambanuzi zinazotolewa katika sura hii.

\(\ln y=\ln\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\)	Hatua ya 1. Chukua logarithm ya asili ya pande zote mbili.
\(\ln y=\ln x+\frac{1}{2}\ln(2x+1)−x\ln e−3\ln \sin x\)	Hatua ya 2. Panua kutumia mali ya logarithms.
\(\dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\dfrac{\cos x}{\sin x}\)	Hatua ya 3. Tofautisha pande zote mbili.
\(\dfrac{dy}{dx}=y\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\)	Hatua ya 4. Kuzidisha kwa\(y\) pande zote mbili.
\(\dfrac{dy}{dx}=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\)	Hatua ya 5. Mbadala\(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}.\)

Zoezi\(\PageIndex{5}\)

Tumia tofauti ya logarithmic ili kupata derivative ya\(y=x^x\).

Kidokezo

Fuata mkakati wa kutatua tatizo.

Jibu

Suluhisho:\(\dfrac{dy}{dx}=x^x(1+\ln x)\)

Zoezi\(\PageIndex{6}\)

Kupata derivative ya\(y=(\tan x)^π\).

Kidokezo

Tumia utawala wa nguvu (tangu exponent\(\pi\) ni mara kwa mara) na utawala wa mnyororo.

Jibu

\(y′=π(\tan x)^{π−1}\sec^2 x\)

Dhana muhimu

• Kwa misingi ya dhana kwamba kazi ya kielelezo\(y=b^x, \,b>0\) inaendelea kila mahali na inatofautiana\(0\), kazi hii inatofautiana kila mahali na kuna formula kwa derivative yake.
• Tunaweza kutumia formula ili kupata derivative ya\(y=\ln x\), na uhusiano\(\log_b x=\dfrac{\ln x}{\ln b}\) inatuwezesha kupanua formula zetu za kutofautisha ili kujumuisha logarithms na misingi ya kiholela.
• Tofauti ya Logarithmic inatuwezesha kutofautisha kazi za fomu\(y=g(x)^{f(x)}\) au kazi ngumu sana kwa kuchukua logarithm ya asili ya pande zote mbili na kutumia mali ya logarithms kabla ya kutofautisha.

Mlinganyo muhimu

• Derivative ya kazi ya asili ya kielelezo

\(\dfrac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x)\)

• Derivative ya kazi ya asili ya logarithmic

\(\dfrac{d}{dx}\Big(\ln g(x)\Big)=\dfrac{1}{g(x)}g′(x)\)

• Derivative ya kazi ya jumla ya maonyesho

\(\dfrac{d}{dx}\Big(b^{g(x)}\Big)=b^{g(x)}g′(x)\ln b\)

• Derivative ya kazi ya jumla ya logarithmic

\(\dfrac{d}{dx}\Big(\log_b g(x)\Big)=\dfrac{g′(x)}{g(x)\ln b}\)

faharasa

tofauti ya logarithmic

ni mbinu ambayo inaruhusu sisi kutofautisha kazi kwa kwanza kuchukua logarithm asili ya pande zote mbili za equation, kutumia mali ya logarithms kurahisisha equation, na kutofautisha kwa uwazi