Skip to main content
Global

3.8: Tofauti thabiti

  1. Last updated
  2. Save as PDF
  • Page ID
    178905

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Malengo ya kujifunza
    • Pata derivative ya kazi ngumu kwa kutumia tofauti thabiti.
    • Tumia tofauti thabiti ili kuamua equation ya mstari wa tangent.

    Tayari tumejifunza jinsi ya kupata usawa wa mistari ya tangent kwa kazi na kiwango cha mabadiliko ya kazi kwa hatua fulani. Katika kesi hizi zote tulikuwa equation wazi kwa ajili ya kazi na kutofautishwa kazi hizi wazi. Tuseme badala yake kwamba tunataka kuamua equation ya mstari tangent kwa Curve holela au kiwango cha mabadiliko ya Curve holela katika hatua. Katika sehemu hii, sisi kutatua matatizo haya kwa kutafuta derivatives ya kazi kwamba kufafanua\(y\) inamanisha katika suala la\(x\).

    Tofauti thabiti

    Katika majadiliano mengi ya hisabati, kama variable tegemezi\(y\) ni kazi ya variable huru\(x\), sisi kueleza y katika suala la\(x\). Kama hii ni kesi, tunasema kwamba\(y\) ni kazi wazi ya\(x\). Kwa mfano, wakati sisi kuandika equation\(y=x^2+1\), sisi ni kufafanua y wazi katika suala la\(x\). Kwa upande mwingine, kama uhusiano kati ya kazi\(y\) na variable\(x\) ni walionyesha kwa equation ambapo\(y\) si walionyesha kabisa katika suala la\(x\), tunasema kwamba equation amefafanua\(y\) inamweka katika suala la\(x\). Kwa mfano, equation\(y−x^2=1\) inafafanua kazi\(y=x^2+1\) kwa uwazi.

    Tofauti thabiti inatuwezesha kupata mteremko wa tangents kwa curves ambazo ni wazi si kazi (zinashindwa mtihani wa mstari wa wima). Sisi ni kutumia wazo kwamba sehemu ya\(y\) ni kazi kwamba kukidhi equation kutokana, lakini y kwamba si kweli kazi ya\(x\).

    Kwa ujumla, equation amefafanua kazi inamweka kama kazi satisfies kwamba equation. Equation inaweza kufafanua kazi nyingi tofauti kwa uwazi. Kwa mfano, kazi

    \[y=\sqrt{25−x^2}\nonumber \]

    na

    \[y=\begin{cases}\sqrt{25−x^2}, & \text{if }−5≤x<0\\ −\sqrt{25−x^2}, & \text{if }0≤x≤5\end{cases}\nonumber \]

    ambayo ni mfano katika Kielelezo\(\PageIndex{1}\), ni mbili tu ya kazi nyingi defined inamaanisha na equation\(x^2+y^2=25\).

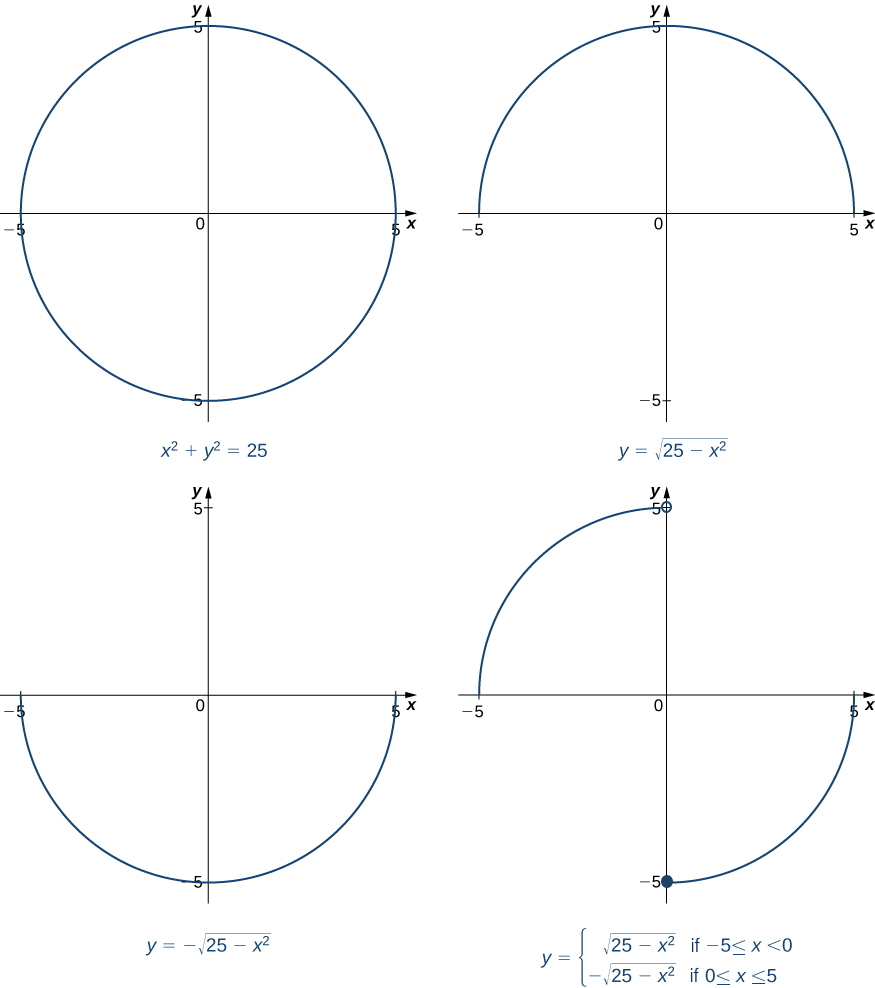
    Viwanja vya kazi 4: mduara wa radius 5 unaozingatia asili, nusu duara ya radius 5 juu ya mhimili x na katikati ya asili, nusu duara ya radius 5 chini x mhimili na katikati ya asili, robo duru ya radius 5 na katikati ya asili katika quadrants 2 na 4
    Takwimu:\(\PageIndex{1}\) Equation inafafanua kazi\(x^2+y^2=25\) nyingi kwa uwazi.

    Kama tunataka kupata mteremko wa mstari tangent kwa grafu ya\(x^2+y^2=25\) katika hatua\((3,4)\), tunaweza kutathmini derivative ya kazi\(y=\sqrt{25−x^2}\) katika\(x=3\). Kwa upande mwingine, kama tunataka mteremko wa mstari tangent katika hatua\((3,−4)\), tunaweza kutumia derivative ya\(y=−\sqrt{25−x^2}\). Hata hivyo, si rahisi kutatua kwa kazi defined inamaanisha kwa equation. Kwa bahati nzuri, mbinu ya upambanuzi thabiti inaruhusu sisi kupata derivative ya kazi inamweka defined bila milele kutatua kwa kazi wazi. Mchakato wa kutafuta\(\dfrac{dy}{dx}\) kwa kutumia upambanuzi thabiti unaelezewa katika mkakati wafuatayo wa kutatua matatizo.

    Mkakati wa Kutatua matatizo: Tofauti thabiti

    Ili kufanya tofauti thabiti juu ya equation inayofafanua kazi\(y\) kwa uwazi katika suala la kutofautiana\(x\), tumia hatua zifuatazo:

    1. Chukua derivative ya pande zote mbili za equation. Kumbuka kwamba\(y\) ni kazi ya\(x\). Kwa hiyo, wakati\[\dfrac{d}{dx}(\sin x)=\cos x\nonumber \] na\[\dfrac{d}{dx}(\sin y)=\cos y\cdot\dfrac{dy}{dx}\nonumber \] kwa sababu ni lazima kutumia utawala mnyororo kutofautisha\(\sin y\) kwa heshima na\(x\).
    2. Andika upya equation ili maneno yote yaliyo\(dy/dx\) na upande wa kushoto na maneno yote ambayo hayana yana yana\(dy/dx\) upande wa kulia.
    3. Factor nje\(dy/dx\) upande wa kushoto.
    4. Kutatua\(dy/dx\) kwa kugawa pande zote mbili za equation kwa kujieleza sahihi algebraic.
    Mfano\(\PageIndex{1}\): Using Implicit Differentiation

    Kutokana kwamba\(y\) ni defined inamaanisha na equation\(x^2+y^2=25\), kupata\(\dfrac{dy}{dx}\).

    Suluhisho

    Fuata hatua katika mkakati wa kutatua matatizo.

    \(\dfrac{d}{dx}(x^2+y^2)=\dfrac{d}{dx}(25)\) Hatua ya 1. Tofauti pande zote mbili za equation.
    \(\dfrac{d}{dx}(x^2)+\dfrac{d}{dx}(y^2)=0\) Hatua ya 1.1. Tumia utawala wa jumla upande wa kushoto. Kwenye haki\(\dfrac{d}{dx}(25)=0\).
    \(2x+2y\dfrac{dy}{dx}=0\) Hatua ya 1.2. Chukua derivatives, hivyo\(\dfrac{d}{dx}(x^2)=2x\) na\(\dfrac{d}{dx}(y^2)=2y\dfrac{dy}{dx}\).
    \(2y\dfrac{dy}{dx}=−2x\) Hatua ya 2. Weka masharti na\(\dfrac{dy}{dx}\) upande wa kushoto. Hoja masharti yaliyobaki kwa haki.
    \(\dfrac{dy}{dx}=−\dfrac{x}{y}\) Hatua ya 4. Gawanya pande zote mbili za equation na\(2y\). (Hatua ya 3 haitumiki katika kesi hii.)

    Uchambuzi

    Kumbuka kuwa kujieleza kusababisha kwa\(\dfrac{dy}{dx}\) ni katika suala la wote variable huru\(x\) na variable tegemezi\(y\). Ingawa katika baadhi ya matukio inaweza kuwa inawezekana kueleza\(\dfrac{dy}{dx}\) kwa suala la\(x\) tu, kwa ujumla haiwezekani kufanya hivyo.

    Mfano\(\PageIndex{2}\): Using Implicit Differentiation and the Product Rule

    Kutokana kwamba\(y\) ni defined inamaanisha na equation\(x^3\sin y+y=4x+3\), kupata\(\dfrac{dy}{dx}\).

    Suluhisho

    \(\dfrac{d}{dx}(x^3\sin y+y)=\dfrac{d}{dx}(4x+3)\) Hatua ya 1: Tofauti pande zote mbili za equation.
    \(\dfrac{d}{dx}(x^3\sin y)+\dfrac{d}{dx}(y)=4\) Hatua ya 1.1: Tumia utawala wa jumla upande wa kushoto. Kwa upande wa kulia,\(\dfrac{d}{dx}(4x+3)=4\).
    \(\left(\dfrac{d}{dx}(x^3)⋅\sin y+\dfrac{d}{dx}(\sin y)⋅x^3\right)+\dfrac{dy}{dx}=4\) Hatua 1.2: Tumia utawala wa bidhaa ili upate\(\dfrac{d}{dx}(x^3\sin y)\). Kuzingatia hilo\(\dfrac{d}{dx}(y)=\dfrac{dy}{dx}\).
    \(3x^2\sin y+(\cos y\dfrac{dy}{dx})⋅x^3+\dfrac{dy}{dx}=4\) Hatua 1.3: Tunajua\(\dfrac{d}{dx}(x^3)=3x^2\). Tumia utawala wa mnyororo ili kupata\(\dfrac{d}{dx}(\sin y)=\cos y\dfrac{dy}{dx}\).
    \(x^3\cos y\dfrac{dy}{dx}+\dfrac{dy}{dx}=4−3x^2\sin y\) Hatua ya 2: Weka masharti yote yaliyo na\(\dfrac{dy}{dx}\) upande wa kushoto. Hoja maneno mengine yote kwa haki.
    \(\dfrac{dy}{dx}(x^3\cos y+1)=4−3x^2\sin y\) Hatua ya 3: Factor nje\(\dfrac{dy}{dx}\) upande wa kushoto.
    \(\dfrac{dy}{dx}=\dfrac{4−3x^2\sin y}{x^3\cos y+1}\) hatua 4: Kutatua\(\dfrac{dy}{dx}\) kwa kugawa pande zote mbili za equation na\(x^3\cos y+1\).
    Mfano\(\PageIndex{3}\): Using Implicit Differentiation to Find a Second Derivative

    Tafuta\(\dfrac{d^2y}{dx^2}\) kama\(x^2+y^2=25\).

    Suluhisho

    Katika Mfano\(\PageIndex{1}\), tulionyesha kuwa\(\dfrac{dy}{dx}=−\dfrac{x}{y}\). Tunaweza kuchukua derivative ya pande zote mbili za equation hii kupata\(\dfrac{d^2y}{dx^2}\).

    \ (\ kuanza {align*}\ dfrac {d ^ 2y} {dx^2} &=\ dfrac {d} {d} {dy}\ kushoto (\ dfrac {x} {y}\ haki) & &\ maandishi {Tofauti pande zote mbili}\ dfrac {dx} {x} {y}.\\ [4pt]
    &=\dfrac {\ kushoto (1y-x\ dfrac {dy} {dx}\ kulia)} {y ^ 2} &\ maandishi {Tumia utawala wa quotient kupata}\ dfrac {d} {dy}\ kushoto (∙\ dfrac {x} {y} \\ [4pt]
    &=\ dfrac {-y+x\ dfrac {dfrac {dx} {y} {y ^ 2} & &\ maandishi {kurahisisha.}\\ [4pt]
    &=\ dfrac {y-y+x\ kushoto (\ dfrac {x} {y}\ haki)} {y ^ 2} & &\ maandishi {mbadala}\ dfrac {dy} {dx} =\ dfrac {x} {y}.\\ [4pt]
    &=\ dfrac {y ^ 2,1x^2} {y ^ 3} & &\ maandishi {Kurahisisha.} \ mwisho {align*}\)

    Katika hatua hii tumepata kujieleza kwa\(\dfrac{d^2y}{dx^2}\). Kama sisi kuchagua, tunaweza kurahisisha kujieleza zaidi kwa kukumbuka kwamba\(x^2+y^2=25\) na kufanya badala hii katika nambari ya kupata\(\dfrac{d^2y}{dx^2}=−\dfrac{25}{y^3}\).

    Zoezi\(\PageIndex{1}\)

    Kupata\(\dfrac{dy}{dx}\) kwa\(y\) defined inamaanisha na equation\(4x^5+\tan y=y^2+5x\).

    Kidokezo

    Fuata mkakati wa kutatua tatizo, kukumbuka kutumia utawala wa mnyororo wa kutofautisha\(\tan y\) na\(y^2\).

    Jibu

    \[\dfrac{dy}{dx}=\dfrac{5−20x^4}{\sec^2y−2y} \nonumber \]

    Kupata Tangent Lines Kimsingi

    Sasa kwa kuwa tumeona mbinu ya upambanuzi thabiti, tunaweza kuitumia kwa tatizo la kutafuta equations ya mistari tangent kwa curves ilivyoelezwa na equations.

    Mfano\(\PageIndex{4}\): Finding a Tangent Line to a Circle

    Find equation ya tangent line Curve\(x^2+y^2=25\) katika hatua\((3,−4)\).

    Suluhisho

    Ingawa tunaweza kupata equation hii bila kutumia tofauti thabiti, kutumia njia hiyo inafanya iwe rahisi zaidi. Katika Mfano\(\PageIndex{1}\), tumegundua\(\dfrac{dy}{dx}=−\dfrac{x}{y}\).

    Mteremko wa mstari wa tangent hupatikana kwa kubadili\((3,−4)\) katika maneno haya. Kwa hiyo, mteremko wa mstari wa tangent ni\(\dfrac{dy}{dx}\Big|_{(3,−4)}=−\dfrac{3}{−4}=\dfrac{3}{4}\).

    Kutumia hatua\((3,−4)\) na mteremko\(\dfrac{3}{4}\) katika usawa wa mteremko wa mstari, tunapata equation\(y=\dfrac{3}{4}x−\dfrac{25}{4}\) (Kielelezo\(\PageIndex{2}\)).

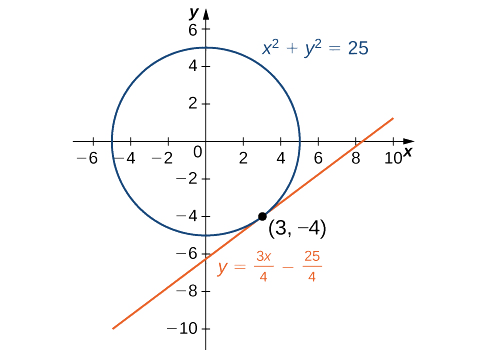
    Mduara na radius 5 na katikati ya asili ni graphed. Mstari wa tangent hutolewa kupitia hatua (3, -4).
    Kielelezo\(\PageIndex{2}\): Mstari\(y=\dfrac{3}{4}x−\dfrac{25}{4}\) ni tangent kwa\(x^2+y^2=25\) hatua (3, -4).
    Mfano\(\PageIndex{5}\): Finding the Equation of the Tangent Line to a Curve

    Kupata equation ya tangent line kwa grafu ya\(y^3+x^3−3xy=0\) katika hatua\(\left(\frac{3}{2},\frac{3}{2}\right)\) (Kielelezo\(\PageIndex{3}\)). Curve hii inajulikana kama folium (au jani) ya Descartes.

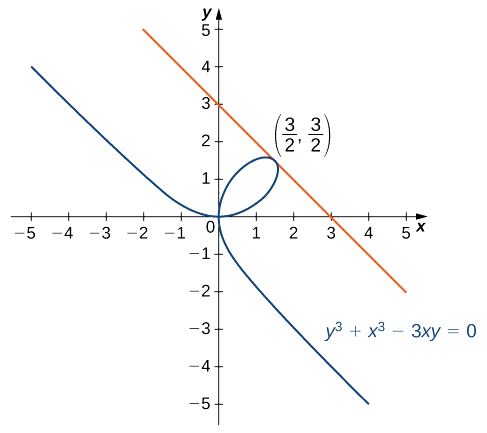
    Foliamu inavyoonyeshwa, ambayo ni mstari unaojenga kitanzi kinachovuka juu ya yenyewe. Katika grafu hii, huvuka juu ya yenyewe (0, 0). Mstari wake wa tangent kutoka (3/2, 3/2) unaonyeshwa.
    Kielelezo\(\PageIndex{3}\): Kupata mstari tangent kwa folium ya Descartes katika\(\left(\frac{3}{2},\frac{3}{2}\right)\).

    Suluhisho

    Anza kwa kutafuta\(\dfrac{dy}{dx}\).

    \(\dfrac{d}{dx}\big(y^3+x^3−3xy\big)=\dfrac{d}{dx}\big(0\big)\)

    \(3y^2\dfrac{dy}{dx}+3x^2−\left(3y+3x\dfrac{dy}{dx}\right)=0\)

    \(3y^2\dfrac{dy}{dx}+3x^2−3y-3x\dfrac{dy}{dx}=0\)

    \(\left(3y^2-3x\right)\dfrac{dy}{dx}=3y-3x^2\)

    \(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\).

    Kisha, badala\(\left(\frac{3}{2},\frac{3}{2}\right)\) ya\(\dfrac{dy}{dx}=\dfrac{3y−3x^2}{3y^2−3x}\) kupata mteremko wa mstari wa tangent:

    \(\dfrac{dy}{dx}\Bigg|_{\left(\frac{3}{2},\frac{3}{2}\right)}=−1\).

    Hatimaye, mbadala katika equation uhakika-mteremko wa mstari wa kupata

    \(y=−x+3\).

    Mfano\(\PageIndex{6}\): Applying Implicit Differentiation

    Katika mchezo rahisi video, roketi husafiri katika obiti elliptical ambao njia ni ilivyoelezwa na equation\(4x^2+25y^2=100\). roketi inaweza moto makombora pamoja mistari tangent kwa njia yake. Lengo la mchezo ni kuharibu asteroid zinazoingia kusafiri pamoja chanya\(x\) -axis kuelekea\((0,0)\). Kama roketi moto kombora wakati iko katika\(\left(3,\frac{8}{5}\right)\), wapi itakuwa intersect\(x\) -axis?

    Suluhisho

    Ili kutatua tatizo hili, ni lazima kuamua ambapo mstari tangent kwa grafu ya

    \(4x^2+25y^2=100\)katika\(\left(3,\frac{8}{5}\right)\) intersects\(x\) -axis. Anza kwa kutafuta\(\dfrac{dy}{dx}\) kwa uwazi.

    Kutofautisha, tuna

    \(8x+50y\dfrac{dy}{dx}=0.\)

    Kutatua kwa\(\dfrac{dy}{dx}\),

    tuna

    \(\dfrac{dy}{dx}=−\dfrac{4x}{25y}\).

    Mteremko wa mstari wa tangent ni\(\dfrac{dy}{dx}\Bigg|_{\left(3,\frac{8}{5}\right)}=−\dfrac{3}{10}\). Ulinganisho wa mstari wa tangent ni\(y=−\dfrac{3}{10}x+\dfrac{5}{2}\). Kuamua wapi mstari unaingilia\(x\) -axis, tatua\(0=−\dfrac{3}{10}x+\dfrac{5}{2}\). Suluhisho ni\(x=\dfrac{25}{3}\). Kombora huingiliana na\(x\) -axis kwenye hatua\(\left(\frac{25}{3},0\right)\).

    Zoezi\(\PageIndex{2}\)

    Kupata equation ya tangent line kwa hyperbola\(x^2−y^2=16\) katika hatua\((5,3)\).

    Kidokezo

    \(\dfrac{dy}{dx}=\dfrac{x}{y}\)

    Jibu

    \(y=\dfrac{5}{3}x−\dfrac{16}{3}\)

    Dhana muhimu

    • Tunatumia upambanuzi thabiti ili kupata derivatives ya kazi zilizoelezwa kwa usahihi (kazi zilizofafanuliwa na milinganyo).
    • Kwa kutumia tofauti thabiti, tunaweza kupata equation ya mstari tangent kwa grafu ya Curve.

    faharasa

    tofauti thabiti
    ni mbinu kwa ajili ya kompyuta\(\dfrac{dy}{dx}\) kwa ajili ya kazi inavyoelezwa na equation, kukamilika kwa kutofautisha pande zote mbili za equation (kukumbuka kutibu variable\(y\) kama kazi) na kutatua kwa\(\dfrac{dy}{dx}\)