3.2: Derivative kama Kazi
- Page ID
- 178921
- Kufafanua kazi derivative ya kazi fulani.
- Grafu kazi ya derivative kutoka kwenye grafu ya kazi iliyotolewa.
- Eleza uhusiano kati ya derivatives na kuendelea.
- Eleza hali tatu kwa wakati kazi haina derivative.
- Eleza maana ya derivative ya juu-ili.
Kama tulivyoona, derivative ya kazi katika hatua fulani inatupa kiwango cha mabadiliko au mteremko wa mstari wa tangent kwa kazi wakati huo. Kama sisi kutofautisha msimamo kazi kwa wakati fulani, sisi kupata kasi kwa wakati huo. Inaonekana busara kuhitimisha kwamba kujua derivative ya kazi katika kila hatua ingeweza kuzalisha taarifa muhimu kuhusu tabia ya kazi. Hata hivyo, mchakato wa kutafuta derivative hata wachache wa maadili kwa kutumia mbinu za sehemu iliyotangulia ingekuwa haraka sana. Katika sehemu hii sisi kufafanua kazi derivative na kujifunza mchakato wa kupata hiyo.
Kazi za derivative
Kazi ya derivative inatoa derivative ya kazi katika kila hatua katika uwanja wa kazi ya awali ambayo derivative inaelezwa. Tunaweza rasmi kufafanua kazi derivative kama ifuatavyo.
Hebu\(f\) kuwa kazi. Kazi ya derivative, iliyoonyeshwa na\(f'\), ni kazi ambayo uwanja wake una maadili\(x\) hayo ya kwamba kikomo kinachofuata kipo:
\[f'(x)=\lim_{h→0}\frac{f(x+h)−f(x)}{h}. \label{derdef} \]
Kazi\(f(x)\) inasemekana kutofautishwa\(a\) ikiwa\(f'(a)\) ipo. Kwa ujumla, kazi inasemekana \(S\)kutofautishwa ikiwa inatofautiana katika kila hatua katika kuweka wazi\(S\), na kazi tofauti ni moja ambayo\(f'(x)\) ipo kwenye uwanja wake.
Katika mifano michache ijayo tunatumia Equation\ ref {derdef} ili kupata derivative ya kazi.
Kupata derivative ya\(f(x)=\sqrt{x}\).
Suluhisho
Anza moja kwa moja na ufafanuzi wa kazi ya derivative.
Mbadala\(f(x+h)=\sqrt{x+h}\) na\(f(x)=\sqrt{x}\) ndani ya\(f'(x)= \displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\).
| \(f'(x)=\displaystyle \lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}\) | |
| \(=\displaystyle\lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}⋅\frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}}\) | Kuzidisha nambari na denominator\(\sqrt{x+h}+\sqrt{x}\) bila kusambaza katika denominator. |
| \(=\displaystyle\lim_{h→0}\frac{h}{h\left(\sqrt{x+h}+\sqrt{x}\right)}\) | Kuzidisha nambari na kurahisisha. |
| \(=\displaystyle\lim_{h→0}\frac{1}{\left(\sqrt{x+h}+\sqrt{x}\right)}\) | Futa\(h\). |
| \(=\dfrac{1}{2\sqrt{x}}\) | Tathmini kikomo |
Pata derivative ya kazi\(f(x)=x^2−2x\).
Suluhisho
Fuata utaratibu huo hapa, lakini bila ya kuongezeka kwa conjugate.
Mbadala\(f(x+h)=(x+h)^2−2(x+h)\) na\(f(x)=x^2−2x\) ndani\(f'(x)= \displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}.\)
| \(f'(x)=\displaystyle\lim_{h→0}\frac{((x+h)^2−2(x+h))−(x^2−2x)}{h}\) | |
| \(=\displaystyle\lim_{h→0}\frac{x^2+2xh+h^2−2x−2h−x^2+2x}{h}\) | Panua\((x+h)^2−2(x+h)\). |
| \(=\displaystyle\lim_{h→0}\frac{2xh−2h+h^2}{h}\) | Rahisisha |
| \(=\displaystyle\lim_{h→0}\frac{h(2x−2+h)}{h}\) | Factor nje\(h\) kutoka kwa nambari |
| \(=\displaystyle\lim_{h→0}(2x−2+h)\) | Kufuta sababu ya kawaida ya\(h\) |
| \(=2x−2\) | Tathmini kikomo |
Kupata derivative ya\(f(x)=x^2\).
- Kidokezo
-
Tumia Equation\ ref {derdef} na ufuate mfano.
- Jibu
-
\(f'(x)=2x\)
Sisi kutumia aina ya nukuu tofauti kueleza derivative ya kazi. Katika Mfano\(\PageIndex{2}\) tulionyesha kwamba kama\(f(x)=x^2−2x\), basi\(f'(x)=2x−2\). Kama tulikuwa walionyesha kazi hii katika fomu\(y=x^2−2x\), tunaweza kuwa walionyesha derivative kama\(y′=2x−2\) au\(\dfrac{dy}{dx}=2x−2\). Tungeweza kufikisha habari sawa kwa kuandika\(\dfrac{d}{dx}\left(x^2−2x\right)=2x−2\). Hivyo, kwa ajili ya kazi\(y=f(x)\), kila moja ya maelezo yafuatayo yanawakilisha derivative ya\(f(x)\):
\(f'(x), \quad \dfrac{dy}{dx}, \quad y′,\quad \dfrac{d}{dx}\big(f(x)\big)\).
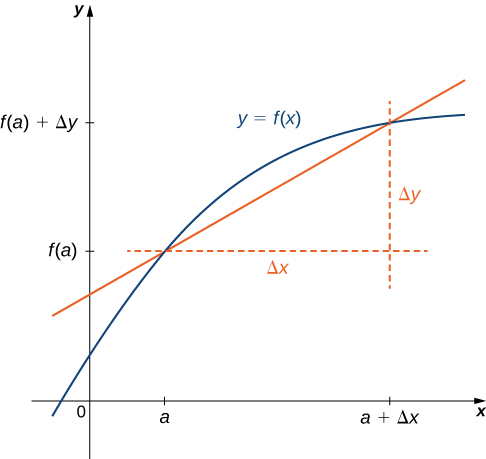
Badala ya\(f'(a)\) sisi pia kutumia\(\dfrac{dy}{dx}\Big|_{x=a}\). Matumizi ya\(\dfrac{dy}{dx}\) notation (inayoitwa Leibniz notation) ni ya kawaida sana katika uhandisi na fizikia. Ili kuelewa notation hii bora, kumbuka kwamba derivative ya kazi katika hatua ni kikomo cha mteremko wa mistari secant kama mistari secant inakaribia mstari tangent. Miteremko ya mistari hii ya salama mara nyingi huonyeshwa kwa fomu\(\dfrac{Δy}{Δx}\) ambapo\(Δy\) tofauti katika\(y\) maadili yanayolingana na tofauti katika\(x\) maadili, ambayo yanaelezwa kama\(Δx\) (Kielelezo\(\PageIndex{1}\)). Hivyo derivative, ambayo inaweza kufikiriwa kama kiwango cha instantaneous ya mabadiliko ya kuhusiana\(y\) na\(x\), ni walionyesha kama
\(\displaystyle \frac{dy}{dx}= \lim_{Δx→0}\frac{Δy}{Δx}\).
Graphing derivative
Tayari kujadiliwa jinsi ya graph kazi, hivyo kutokana na equation ya kazi au equation ya kazi derivative, tunaweza graph yake. Kutokana na wote wawili, tunatarajia kuona mawasiliano kati ya grafu ya kazi hizi mbili, tangu\(f'(x)\) anatoa kiwango cha mabadiliko ya kazi\(f(x)\) (au mteremko wa mstari wa tangent kwa\(f(x)\)).
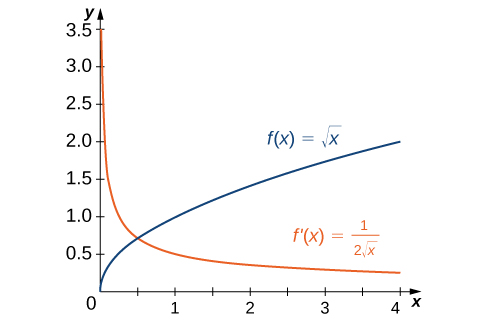
Katika Mfano\(\PageIndex{1}\), tuligundua kwamba kwa\(f(x)=\sqrt{x}\),\(f'(x)=\frac{1}{2\sqrt{x}}\). Ikiwa tunapiga kazi hizi kwenye shaba sawa, kama katika Kielelezo\(\PageIndex{2}\), tunaweza kutumia grafu kuelewa uhusiano kati ya kazi hizi mbili. Kwanza, tunaona kwamba\(f(x)\) inaongezeka juu ya uwanja wake wote, ambayo ina maana kwamba mteremko wa mistari yake ya tangent wakati wote ni chanya. Kwa hiyo, tunatarajia\(f'(x)>0\) maadili yote ya x katika uwanja wake. Zaidi ya hayo, kama\(x\) ongezeko, mteremko wa mistari tangent kwa\(f(x)\) ni kupungua na tunatarajia kuona kupungua sambamba katika\(f'(x)\). Sisi pia kuchunguza kwamba\(f(0)\) ni undefined na kwamba\(\displaystyle \lim_{x→0^+}f'(x)=+∞\), sambamba na tangent wima kwa\(f(x)\) saa\(0\).
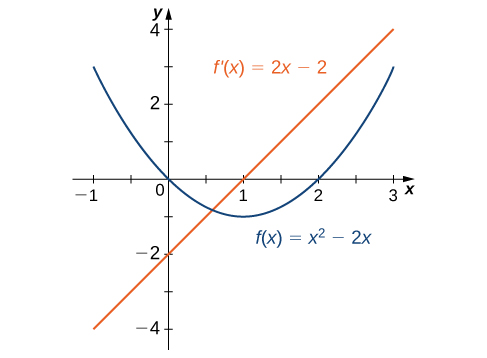
Katika Mfano\(\PageIndex{2}\), tuligundua kwamba kwa\(f(x)=x^2−2x,\; f'(x)=2x−2\). Grafu za kazi hizi zinaonyeshwa kwenye Kielelezo\(\PageIndex{3}\). Kuzingatia kwamba\(f(x)\) ni kupungua kwa\(x<1\). Kwa maadili haya sawa ya\(x\),\(f'(x)<0\). Kwa maadili ya\(x>1\),\(f(x)\) ni kuongezeka na\(f'(x)>0\). Pia,\(f(x)\) ina tangent ya usawa\(x=1\) na\(f'(1)=0\).
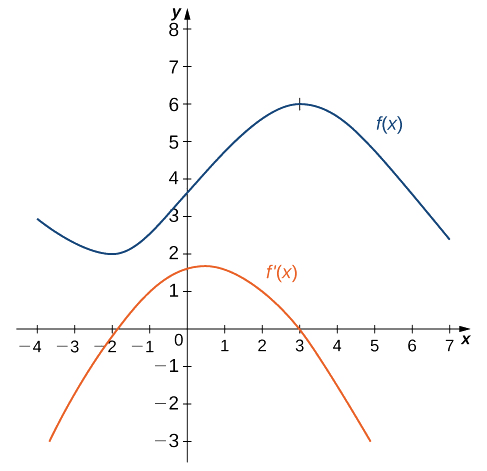
Tumia graph ifuatayo\(f(x)\) ya mchoro grafu ya\(f'(x)\).
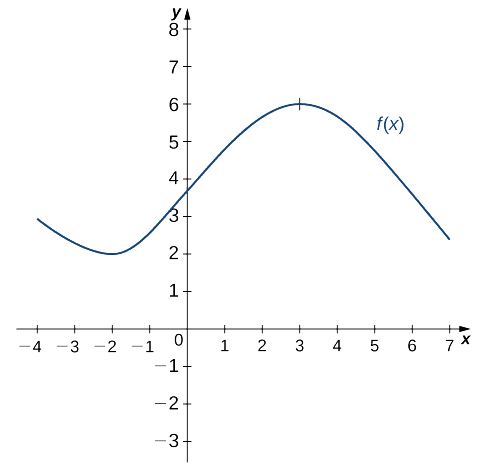
Suluhisho
Suluhisho linaonyeshwa kwenye grafu ifuatayo. Kuzingatia kwamba\(f(x)\) ni kuongezeka na\(f'(x)>0\) kuendelea\((–2,3)\). Pia,\(f(x)\) ni kupungua na\(f'(x)<0\) kuendelea\((−∞,−2)\) na kuendelea\((3,+∞)\). Pia kumbuka kuwa\(f(x)\) ina tangents usawa katika\(–2\) na\(3\), na\(f'(−2)=0\) na\(f'(3)=0\).
Mchoro grafu ya\(f(x)=x^2−4\). Kwa muda gani ni grafu ya\(f'(x)\) juu ya\(x\) -axis?
- Kidokezo
-
Grafu ya\(f'(x)\) ni chanya ambapo\(f(x)\) inaongezeka.
- Jibu
-
\((0,+∞)\)
Derivatives na kuendelea
Sasa kwa kuwa tunaweza kuchora derivative, hebu tuchunguze tabia ya grafu. Kwanza, tunazingatia uhusiano kati ya kutofautisha na kuendelea. Tutaona kwamba kama kazi ni tofauti katika hatua, ni lazima kuendelea huko; hata hivyo, kazi inayoendelea katika hatua haipaswi kutofautishwa wakati huo. Kwa kweli, kazi inaweza kuendelea kwa hatua na kushindwa kutofautishwa kwa hatua kwa moja ya sababu kadhaa.
Hebu\(f(x)\) kuwa kazi na\(a\) uwe katika uwanja wake. Kama\(f(x)\) ni kutofautisha katika\(a\), basi\(f\) ni kuendelea katika\(a\).
Kama\(f(x)\) ni differentiable katika\(a\), basi\(f'(a)\) ipo na, kama sisi basi\(h = x - a\), tuna\( x = a + h \), na kama\(h=x-a\to 0\), tunaweza kuona kwamba\(x\to a\).
Kisha
\[ f'(a) = \lim_{h\to 0}\frac{f(a+h)-f(a)}{h}\nonumber \]
inaweza kuandikwa upya kama
\(f'(a)=\displaystyle \lim_{x→a}\frac{f(x)−f(a)}{x−a}\).
Tunataka kuonyesha kwamba\(f(x)\) ni kuendelea katika\(a\) kwa kuonyesha kwamba\(\displaystyle \lim_{x→a}f(x)=f(a).\) Hivyo,
\ (\ kuanza {align*}\ displaystyle\ lim_ {x→ a} f (x) &=\ lim_ {x→ a}\;\ kubwa (f (x) -f (a) +f (a)\ kubwa)\\ [4pt]
&=\ lim_ {x→ a}\ kushoto (\ frac {f (x) -f (a)} {x-a}} (x-a) +f (a)\ haki) & &\ maandishi {Kuzidisha na ugawanye} (f (x) -f (a))\ maandishi {na} x-a.\\ [4pt]
&=\ kushoto (\ lim_ {x→ a}\ frac {f (x) -f (a)} {x-a}\ haki) kushoto (\ lim_ {x→ a}\; (x-a)\ kulia) +\ lim_ {x→ a} f (a)\\ [4pt]
&=f' (a) 0+f (a)\\ [4pt]
&=f (a). \ mwisho {align*}\)
Kwa hiyo, tangu\(f(a)\) ni defined na\(\displaystyle \lim_{x→a}f(x)=f(a)\), sisi kuhitimisha kwamba\(f\) ni kuendelea katika\(a\).
□
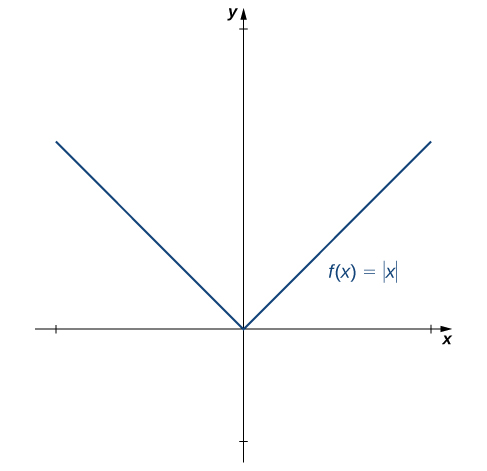
Tumeonyesha tu kwamba kutofautisha ina maana ya kuendelea, lakini sasa tunazingatia kama kuendelea kunamaanisha kutofautisha. Kuamua jibu la swali hili, tunachunguza kazi\(f(x)=|x|\). Kazi hii inaendelea kila mahali; hata hivyo,\(f'(0)\) haijulikani. Uchunguzi huu unatuongoza kuamini kwamba kuendelea haimaanishi kutofautisha. Hebu tuchunguze zaidi. Kwa\(f(x)=|x|\),
\(f'(0)=\displaystyle \lim_{x→0}\frac{f(x)−f(0)}{x−0}= \lim_{x→0}\frac{|x|−|0|}{x−0}= \lim_{x→0}\frac{|x|}{x}\).
Kikomo hii haipo kwa sababu
\(\displaystyle \lim_{x→0^−}\frac{|x|}{x}=−1\)na\(\displaystyle \lim_{x→0^+}\frac{|x|}{x}=1\).
Angalia Kielelezo\(\PageIndex{4}\).
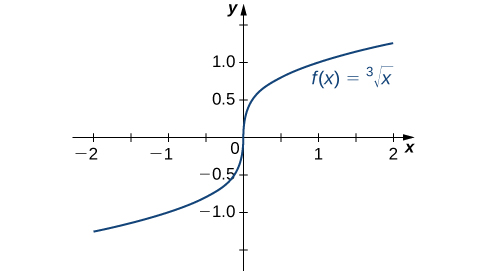
Hebu fikiria baadhi ya hali za ziada ambazo kazi inayoendelea inashindwa kutofautishwa. Fikiria kazi\(f(x)=\sqrt[3]{x}\):
\(f'(0)=\displaystyle \lim_{x→0}\frac{\sqrt[3]{x}−0}{x−0}=\displaystyle \lim_{x→0}\frac{1}{\sqrt[3]{x^2}}=+∞\).
Hivyo\(f'(0)\) haipo. Kuangalia haraka kwenye grafu ya\(f(x)=\sqrt[3]{x}\) kufafanua hali hiyo. Kazi ina mstari wa tangent wima\(0\) (Kielelezo\(\PageIndex{5}\)).
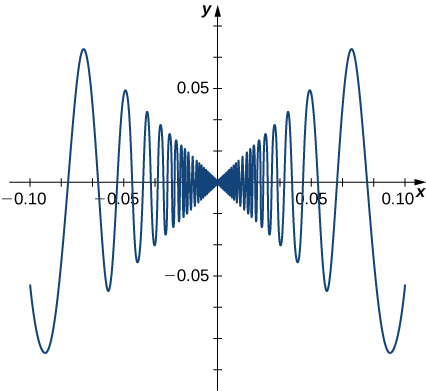
kazi\(f(x)=\begin{cases} x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & & \text{ if } x=0\end{cases}\) pia ina derivative kwamba inaonyesha tabia ya kuvutia katika\(0\).
Tunaona kwamba
\(f'(0)=\displaystyle \lim_{x→0}\frac{x\sin\left(1/x\right)−0}{x−0}= \lim_{x→0}\sin\left(\frac{1}{x}\right)\).
Kikomo hiki haipo, kimsingi kwa sababu mteremko wa mistari ya salama hubadilika mwelekeo wakati wanakaribia sifuri (Kielelezo\(\PageIndex{6}\)).
Kwa muhtasari:
- Tunaona kwamba ikiwa kazi haiendelei, haiwezi kutofautishwa, kwani kila kazi inayofafanuliwa lazima iendelee. Hata hivyo, ikiwa kazi inaendelea, bado inaweza kushindwa kutofautishwa.
- Tuliona kwamba\(f(x)=|x|\) imeshindwa kutofautishwa kwa\(0\) sababu kikomo cha mteremko wa mistari ya tangent upande wa kushoto na kulia haukuwa sawa. Kuangalia, hii ilisababisha kona mkali kwenye grafu ya kazi katika\(0.\) Kutoka hili tunahitimisha kuwa ili kutofautishwa kwa hatua, kazi lazima iwe “laini” wakati huo.
- Kama tulivyoona katika mfano wa\(f(x)=\sqrt[3]{x}\), kazi inashindwa kutofautishwa wakati ambapo kuna mstari wa tangent wima.
- Kama\(f(x)=\begin{cases}x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & &\text{ if } x=0\end{cases}\) tulivyoona na kazi inaweza kushindwa kutofautishwa katika hatua katika njia ngumu zaidi pia.
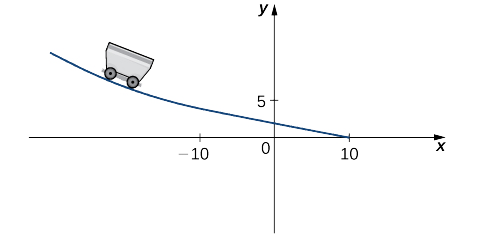
Kampuni ya toy inataka kuunda wimbo kwa gari la toy ambalo linaanza kando ya pembe ya parabolic na kisha hubadilisha mstari wa moja kwa moja (Kielelezo\(\PageIndex{7}\)). Kazi inayoelezea wimbo ni kuwa na fomu\(f(x)=\begin{cases}\frac{1}{10}x^2+bx+c, & & \text{ if }x<−10\\−\frac{1}{4}x+\frac{5}{2}, & & \text{ if } x≥−10\end{cases}\) ambapo\(x\) na\(f(x)\) ni katika inchi. Kwa gari ili kusonga vizuri kwenye wimbo, kazi\(f(x)\) lazima iwe ya kuendelea na kutofautishwa\(−10\). Kupata maadili ya\(b\) na\(c\) kwamba kufanya\(f(x)\) wote kuendelea na kutofautisha.
Suluhisho
Kwa kazi ya kuendelea katika\(x=−10\),\(\displaystyle \lim_{x→10^−}f(x)=f(−10)\). Hivyo, tangu
\(\displaystyle \lim_{x→−10^−}f(x)=\frac{1}{10}(−10)^2−10b+c=10−10b+c\)
na\(f(−10)=5\), ni lazima kuwa na\(10−10b+c=5\). Equivalently, tuna\(c=10b−5\).
Kwa kazi ya kuwa tofauti katika\(−10\),
\(f'(10)=\displaystyle \lim_{x→−10}\frac{f(x)−f(−10)}{x+10}\)
lazima kuwepo. Kwa kuwa\(f(x)\) inafafanuliwa kwa kutumia sheria tofauti upande wa kulia na wa kushoto, lazima tathmini kikomo hiki kutoka kulia na kushoto na kisha tuwaweke sawa na kila mmoja:
\ (\ displaystyle\ kuanza {align*}\ lim_ {x→ -10^}\ frac {f (x) -f (-10)} {x+10} &=\ lim_ {x→ ,1-10^}\ frac {\ frac {1} {10} {10} x ^ 2+c-5} {x+10}\\ [4pt]
&=\ lim_ {x→ -10^}\ frac {1} {10} x ^ 2+bx+ (10b-5) -5} {x+10} &\ maandishi {mbadala} c=10b-5.\\ [4pt]
&=\ lim_ {x→ -10^ї}\ frac {x^2,100+10bx+ 100b} {10 (x+10)}\\ [4pt]
&=\ lim_ {x→ ,110 ^}\ frac {(x+10) (x-10+10b)} {10 (x+10)} & &\ maandishi {Factor kwa kikundi}\\ [4pt]
&=b-1\ mwisho {align*}\).
Pia tuna
\ (\ displaystyle\ kuanza {align*}\ lim_ {x→ -10^+}\ frac {f (x) -f (-10)} {x+10} &=\ lim_ {x→ -10^+}\ frac {}\ frac {4} {4} x+\ frac {5} {2} -5} {x+10}\\ [4pt]
&=\ lim_ {x→ -10^+}\ frac {- (x+10)} {4 (x+10)}\\ [4pt]
&=\ Frac {1} {4}\ mwisho {align*}\).
Hii inatupa\(b−2=−\frac{1}{4}\). Hivyo\(b=\frac{7}{4}\) na\(c=10(\frac{7}{4})−5=\frac{25}{2}\).
Kupata maadili ya a na b kwamba kufanya\(f(x)=\begin{cases}ax+b, & & \text{ if } x<3\\x^2, & & \text{ if } x≥3\end{cases}\) wote kuendelea na kutofautisha katika\(3\).
- Kidokezo
-
Tumia Mfano\(\PageIndex{4}\) kama mwongozo.
- Jibu
-
\(a=6\)na\(b=−9\)
Derivatives ya juu
derivative ya kazi yenyewe ni kazi, hivyo tunaweza kupata derivative ya derivative. Kwa mfano, derivative ya kazi ya msimamo ni kiwango cha mabadiliko ya msimamo, au kasi. Derivative ya kasi ni kiwango cha mabadiliko ya kasi, ambayo ni kuongeza kasi. Kazi mpya iliyopatikana kwa kutofautisha derivative inaitwa derivative ya pili. Zaidi ya hayo, tunaweza kuendelea kuchukua derivatives kupata derivative tatu, derivative nne, na kadhalika. Kwa pamoja, hizi hujulikana kama derivatives ya juu-ili. Notation kwa derivatives ya juu ya utaratibu wa\(y=f(x)\) inaweza kuelezwa katika aina yoyote yafuatayo:
\(f''(x),\; f'''(x),\; f^{(4)}(x),\; …\; ,\; f^{(n)}(x)\)
\(y''(x),\; y'''(x),\; y^{(4)}(x),\; …\; ,\; y^{(n)}(x)\)
\(\dfrac{d^2y}{dx^2},\;\dfrac{d^3y}{dy^3},\;\dfrac{d^4y}{dy^4},\;…\;,\;\dfrac{d^ny}{dy^n}.\)
Inashangaza kutambua kwamba notation kwa\(\dfrac{d^2y}{dx^2}\) inaweza kutazamwa kama jaribio la kueleza\(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\) zaidi compactly.
Analoguous,\(\dfrac{d}{dx}\left(\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)\right)=\dfrac{d}{dx}\left(\dfrac{d^2y}{dx^2}\right)=\dfrac{d^3y}{dx^3}\).
Kwa\(f(x)=2x^2−3x+1\), kupata\(f''(x)\).
Suluhisho
Pata kwanza\(f'(x)\).
Mbadala\(f(x)=2x^2−3x+1\) na\(f(x+h)=2(x+h)^2−3(x+h)+1\) ndani\(f'(x)=\displaystyle \lim_{h→0}\dfrac{f(x+h)−f(x)}{h}.\)
| \(f'(x)=\displaystyle \lim_{h→0}\frac{(2(x+h)^2−3(x+h)+1)−(2x^2−3x+1)}{h}\) | |
| \(=\displaystyle \lim_{h→0}\frac{4xh+2h^2−3h}{h}\) | Kurahisisha nambari. |
| \(=\displaystyle \lim_{h→0}(4x+2h−3)\) | Factor nje\(h\) katika nambari na kufuta na\(h\) katika denominator. |
| \(=4x−3\) | Chukua kikomo. |
Next, kupata\(f''(x)\) kwa kuchukua derivative ya\(f'(x)=4x−3.\)
| \(f''(x)=\displaystyle \lim_{h→0}\frac{f'(x+h)−f'(x)}{h}\) | Tumia\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\)\(f ′(x)\) na badala ya\(f(x).\) |
| \(=\displaystyle \lim_{h→0}\frac{(4(x+h)−3)−(4x−3)}{h}\) | Mbadala\(f'(x+h)=4(x+h)−3\) na\(f'(x)=4x−3.\) |
| \(=\displaystyle \lim_{h→0}4\) | Kurahisisha. |
| \(=4\) | Chukua kikomo. |
Kupata\(f''(x)\) kwa ajili ya\(f(x)=x^2\).
- Kidokezo
-
Tulipata\(f'(x)=2x\) katika checkpoint uliopita. Matumizi Equation\ ref {derdef} kupata derivative ya\(f'(x)\)
- Jibu
-
\(f''(x)=2\)
Msimamo wa chembe kando ya mhimili wa kuratibu kwa wakati\(t\) (kwa sekunde) hutolewa na\(s(t)=3t^2−4t+1\) (kwa mita). Pata kazi inayoelezea kasi yake kwa wakati\(t\).
Suluhisho
Tangu\(v(t)=s′(t)\) na\(a(t)=v′(t)=s''(t)\), tunaanza kwa kutafuta derivative ya\(s(t)\):
\ (\ displaystyle\ kuanza {align*} s (t) &=\ lim_ {h → 0}\ frac {s (t+h) -s (t)} {h}\\ [4pt]
&=\ lim_ {h → 0}\ frac {3 (t+h) ^2,14 (t+h) +1 (3t ^ 2,14t+1)} {h}\\ [4pt]
&=6t-4. \ mwisho {align*}\)
Ifuatayo,
\ (\ displaystyle\ kuanza {align*} s "(t) &=\ lim_ {h → 0}\ frac {s (t+h) -s′ (t)} {h}\\ [4pt]
&=\ lim_ {h → 0}\ frac {6 (t+h) -4)} {h}\\ [4pt]
&=6. \ mwisho {align*}\)
Hivyo,\(a=6 \;\text{m/s}^2\).
Kwa\(s(t)=t^3\), tafuta\(a(t).\)
- Kidokezo
-
Tumia Mfano\(\PageIndex{6}\) kama mwongozo.
- Jibu
-
\(a(t)=6t\)
Dhana muhimu
- Derivative ya kazi\(f(x)\) ni kazi ambayo thamani yake\(x\) ni\(f'(x)\).
- Grafu ya derivative ya kazi\(f(x)\) ni kuhusiana na grafu ya\(f(x)\). Ambapo\(f(x)\) ina mstari wa tangent na mteremko mzuri,\(f'(x)>0\). Ambapo\(f(x)\) ina mstari wa tangent na mteremko hasi,\(f'(x)<0\). Ambapo\(f(x)\) ina mstari wa tangent usio na usawa,\(f'(x)=0.\)
- Ikiwa kazi inatofautiana kwa hatua, basi inaendelea wakati huo. Kazi haipatikani kwa hatua ikiwa haiendelei wakati huo, ikiwa ina mstari wa tangent wima kwenye hatua, au ikiwa grafu ina kona kali au cusp.
- Derivatives ya juu ya utaratibu ni derivatives ya derivatives, kutoka\(n^{\text{th}}\) derivative pili
Mlinganyo muhimu
- Kazi ya derivative
\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\)
faharasa
- kazi ya derivative
- hutoa derivative ya kazi katika kila hatua katika uwanja wa kazi ya awali ambayo derivative inaelezwa
- kutofautishwa katika\(a\)
- kazi ambayo\(f'(a)\) ipo inatofautiana\(a\)
- kutofautishwa juu\(S\)
- kazi ambayo\(f'(x)\) ipo kwa kila mmoja\(x\) katika kuweka wazi\(S\) ni tofauti\(S\)
- kazi inayoweza kutofautishwa
- kazi ambayo\(f'(x)\) ipo ni kazi tofauti
- derivative ya juu-ili
- derivative ya derivative, kutoka derivative ya pili kwa\(n^{\text{th}}\) derivative, inaitwa derivative ya juu-ili
Wachangiaji na Majina
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College) added explanation of the alternative definition of the derivative used in the proof of that differentiability implies continuity.


