3.1: Kufafanua Derivative

Last updated
Save as PDF

Page ID: 178913

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Tambua maana ya tangent kwa pembe kwa hatua.
Tumia mteremko wa mstari wa tangent.
Kutambua derivative kama kikomo cha tofauti quotient.
Tumia derivative ya kazi iliyotolewa kwa hatua.
Eleza kasi kama kiwango cha mabadiliko.
Eleza tofauti kati ya kasi ya wastani na kasi ya haraka.
Tathmini derivative kutoka meza ya maadili.

Sasa kwa kuwa tuna ufahamu wa dhana ya kikomo na uwezo wa vitendo wa kukokotoa mipaka, tumeanzisha msingi wa utafiti wetu wa calculus, tawi la hisabati ambalo tunakokotoa derivatives na integrals. Wanahisabati wengi na wanahistoria wanakubaliana kwamba calculus ilitengenezwa kwa kujitegemea na Mwingereza Isaac Newton (1643—1727) na Mjerumani Gottfried Leibniz (1646—1716), ambaye picha zake zinaonekana kwenye Kielelezo$\PageIndex{1}$. Wakati sisi mikopo Newton na Leibniz na kuendeleza calculus, sisi ni kweli akimaanisha ukweli kwamba Newton na Leibniz walikuwa wa kwanza kuelewa uhusiano kati ya derivative na muhimu. Wote wanahisabati walifaidika na kazi ya watangulizi, kama vile Barrow, Fermat, na Cavalieri. Uhusiano wa awali kati ya wanahisabati wawili huonekana kuwa wa kirafiki; hata hivyo, katika miaka ya baadaye utata mkali ulianza juu ya kazi yao ilichukua kipaumbele. Ingawa inaonekana uwezekano kwamba Newton alifanya, kwa kweli, kufika mawazo nyuma ya calculus kwanza, sisi ni mzigo wa madeni kwa Leibniz kwa notation kwamba sisi kawaida kutumia leo.

Picha za Newton na Leibniz. — Kielelezo$\PageIndex{1}$: Newton na Leibniz wanajulikana kwa kuendeleza calculus kwa kujitegemea.

Tangent mistari

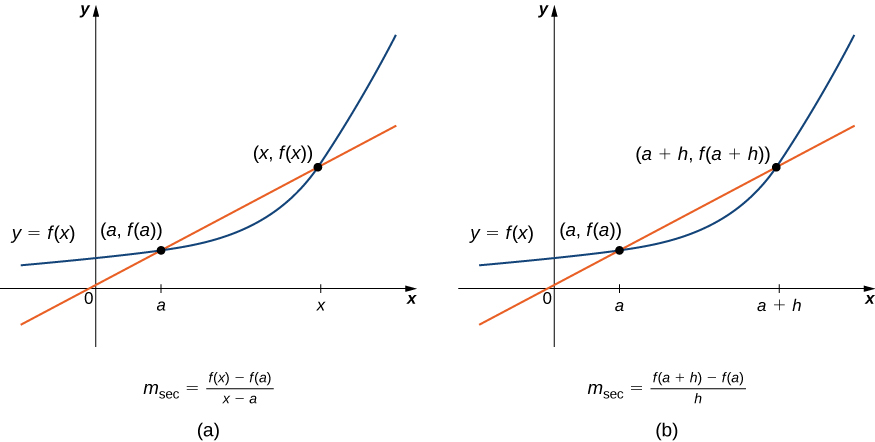
Tunaanza utafiti wetu wa calculus kwa kutafakari tena dhana ya mistari ya salama na mistari ya tangent. Kumbuka kwamba tulitumia mteremko wa mstari secant kwa kazi katika hatua ya$(a,f(a))$ kukadiria kiwango cha mabadiliko, au kiwango ambacho variable moja mabadiliko kuhusiana na variable mwingine. Tunaweza kupata mteremko wa secant kwa kuchagua thamani ya x karibu na kuchora mstari kupitia pointi$(a,f(a))$ na$(x,f(x))$, kama inavyoonekana katika Kielelezo$\PageIndex{2}$. Mteremko wa mstari huu unatolewa na equation kwa namna ya tofauti ya quotient:

\[m_{sec}=\frac{f(x)−f(a)}{x−a} \nonumber \]

Pia unaweza mahesabu ya mteremko wa mstari secant kwa kazi katika thamani a kwa kutumia equation hii$x$ na kuchukua nafasi kwa$a+h$, ambapo$h$ ni thamani karibu na. kisha unaweza mahesabu ya mteremko wa mstari kwa njia ya pointi$(a,f(a))$ na$(a+h,f(a+h))$. Katika kesi hii, tunapata mstari wa secant ina mteremko uliotolewa na tofauti zifuatazo quotient na increment$h$:

\[m_{sec}=\frac{f(a+h)−f(a)}{a+h−a}=\frac{f(a+h)−f(a)}{h} \nonumber \]

Ufafanuzi: Tofauti Quotient

Hebu$f$ kuwa kazi defined juu ya muda$I$ zenye$a$. Ikiwa$x≠a$ iko$I$, basi

\[Q=\frac{f(x)−f(a)}{x−a} \nonumber \]

ni tofauti quotient.

Pia, kama$h≠0$ ni kuchaguliwa hivyo kwamba$a+h$ ni katika$I$, basi

\[Q=\frac{f(a+h)−f(a)}{h} \nonumber \]

ni tofauti quotient na nyongeza$h$.

Maneno haya mawili ya kuhesabu mteremko wa mstari wa salama yanaonyeshwa kwenye Kielelezo$\PageIndex{2}$. Tutaona kwamba kila njia hizi mbili za kutafuta mteremko wa mstari wa salama ni ya thamani. Kulingana na mipangilio, tunaweza kuchagua moja au nyingine. Kuzingatia msingi katika uchaguzi wetu kwa kawaida hutegemea urahisi wa hesabu.

alt — Kielelezo$\PageIndex{2}$: Tunaweza kuhesabu mteremko wa mstari wa salama kwa njia moja mbili.

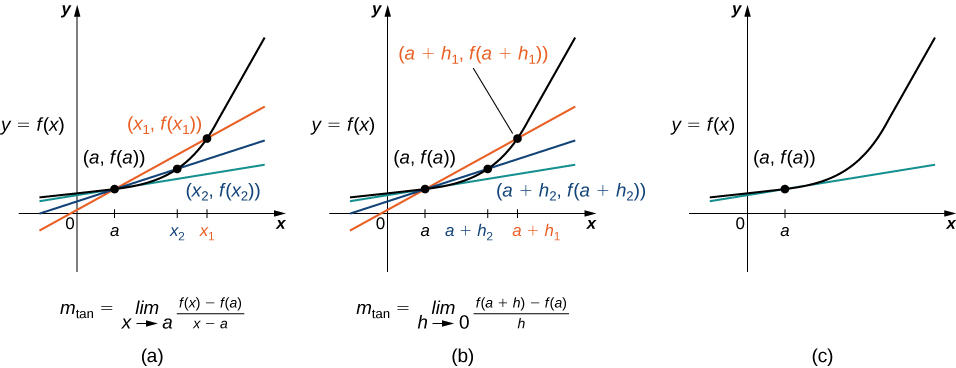
Katika Kielelezo$\PageIndex{3a}$ tunaona kwamba, kama maadili ya$x$ mbinu$a$, mteremko wa mistari ya secant hutoa makadirio bora ya kiwango cha mabadiliko ya kazi saa$a$. Zaidi ya hayo, mistari secant wenyewe mbinu line tangent kwa kazi katika$a$, ambayo inawakilisha kikomo ya mistari secant. Vile vile, Kielelezo$\PageIndex{3b}$ kinaonyesha kwamba kama maadili ya$h$ kupata karibu na$0$, mistari ya secant pia inakaribia mstari wa tangent. Mteremko wa mstari wa tangent$a$ ni kiwango cha mabadiliko ya kazi$a$, kama inavyoonekana kwenye Mchoro$\PageIndex{3c}$.

Takwimu hii ina grafu tatu kinachoitwa a, b, na c. takwimu inaonyesha Cartesian kuratibu ndege na 0, a, x2, na x1 alama ili juu ya x-mhimili. Kuna safu iliyoandikwa y = f (x) yenye alama (a, f (a)), (x2, f (x2)), na (x1, f (x1)). Kuna mistari mitatu ya moja kwa moja: misalaba ya kwanza (a, f (a)) na (x1, f (x1)); misalaba ya pili (a, f (a)) na (x2, f (x2)); na ya tatu inagusa tu (a, f (a)), na kuifanya kuwa tangent. Chini ya grafu, equation mtan = limx → a (f (x) - f (a))/(x - a) hutolewa. Kielelezo b kinaonyesha grafu sawa, lakini wakati huu a + h2 na h1 + ni alama kwenye x-axis badala ya x2 na x1. Kwa hiyo, Curve iliyoandikwa y = f (x) hupita kupitia (a, f (a)), (a + h2, f (a + h2)), na (a + h1, f (a + h1)) na mistari sawa sawa huvuka grafu kama kwenye Kielelezo a Chini ya grafu, equation mtan = limh → 0 (f (a + h) - f (a)) /h inapewa. Kielelezo c kinaonyesha tu safu iliyoandikwa y = f (x) na tangent yake kwa uhakika (a, f (a)). — Kielelezo$\PageIndex{3}$: Mstari wa salama unakaribia mstari wa tangent (umeonyeshwa kwa kijani) kama hatua ya pili inakaribia kwanza.

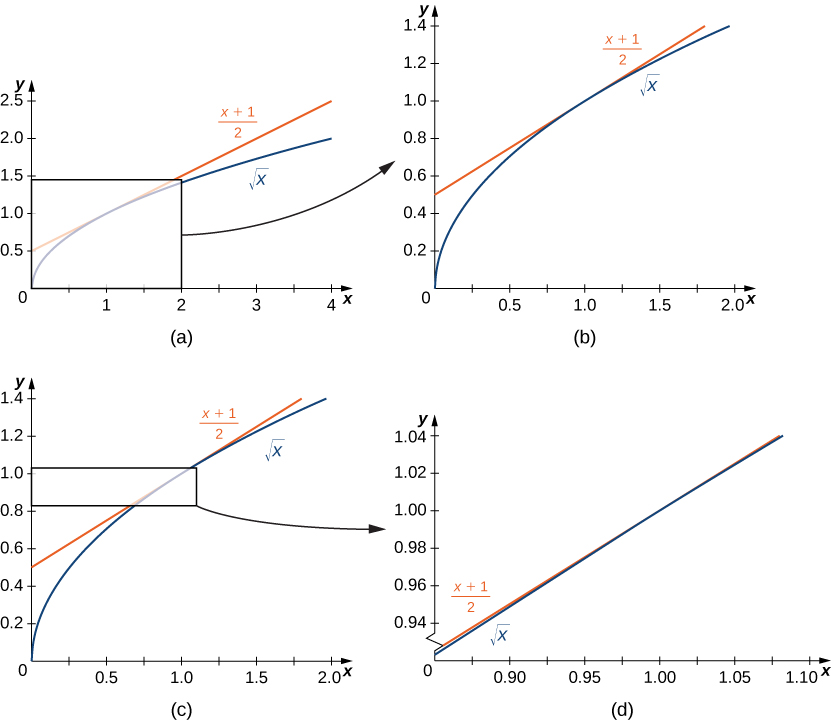
Katika Kielelezo$\PageIndex{4}$ sisi kuonyesha grafu ya$f(x)=\sqrt{x}$ na mstari wake tangent$(1,1)$ katika mfululizo wa vipindi stramare kuhusu$x=1$. Kama vipindi kuwa nyembamba, grafu ya kazi na mstari wake wa tangent huonekana kuwa sanjari, na kufanya maadili kwenye mstari wa tangent kuwa makadirio mazuri kwa maadili ya kazi kwa uchaguzi wa$x$ karibu$1$. Kwa kweli, grafu$f(x)$ yenyewe inaonekana kuwa ndani ya nchi linear katika maeneo ya karibu ya$x=1$.

Takwimu hii ina grafu nne zilizoandikwa a, b, c, na d. takwimu inaonyesha grafu ya mizizi mraba ya x na equation y = (x + 1) /2 na x-axis kwenda kutoka 0 hadi 4 na y-mhimili kwenda kutoka 0 hadi 2.5. Grafu za kazi hizi mbili zinaonekana karibu sana karibu na 1; kuna sanduku karibu ambapo grafu hizi zinaonekana karibu. Kielelezo b inaonyesha karibu juu ya kazi hizi mbili katika eneo la sanduku kutoka Kielelezo a, hasa x kwenda kutoka 0 hadi 2 na y kwenda 0 hadi 1.4. Kielelezo c ni grafu sawa na Kielelezo b, lakini hii ina sanduku kutoka 0 hadi 1.1 katika kuratibu x na 0.8 na 1 kwenye kuratibu y. Kuna mshale unaoonyesha kwamba hii imepigwa kwenye Kielelezo d. takwimu d inaonyesha picha ya karibu sana ya sanduku kutoka Kielelezo c, na kazi mbili zinaonekana kuwa kugusa kwa karibu urefu mzima wa grafu. — Kielelezo$\PageIndex{4}$: Kwa maadili ya$x$ karibu$1$, grafu ya$f(x)=\sqrt{x}$ na mstari wake wa tangent huonekana kuwa sanjari.

Rasmi tunaweza kufafanua mstari tangent kwa grafu ya kazi kama ifuatavyo.

Ufafanuzi: Tangent Line

Hebu$f(x)$ iwe kazi iliyoelezwa katika kipindi cha wazi kilicho na$a$. Mstari wa tangent kwa$f(x)$ saa$a$ ni mstari unaopita kupitia hatua$(a,f(a))$ iliyo na mteremko

\[m_{tan}=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \label{tanline1} \]

zinazotolewa kikomo hii ipo.

Equivalently, tunaweza kufafanua line tangent$a$ kwa$f(x)$ saa kuwa line kupita kwa njia ya uhakika$(a,f(a))$ kuwa mteremko

\[m_{tan}=\lim_{h→0}\frac{f(a+h)−f(a)}{h} \label{tanline2} \]

zinazotolewa kikomo hii ipo.

Kama vile tulivyotumia maneno mawili tofauti kufafanua mteremko wa mstari wa secant, tunatumia aina mbili tofauti ili kufafanua mteremko wa mstari wa tangent. Katika maandishi haya tunatumia aina zote mbili za ufafanuzi. Kama hapo awali, uchaguzi wa ufafanuzi utategemea mipangilio. Sasa kwa kuwa tuna rasmi defined line tangent kwa kazi katika hatua, tunaweza kutumia ufafanuzi huu kupata equations ya mistari tangent.

Mfano$\PageIndex{1}$: Finding a Tangent Line

Kupata equation ya tangent line kwa grafu ya$f(x)=x^2$ saa$x=3.$

Suluhisho

Kwanza kupata mteremko wa mstari wa tangent. Katika mfano huu, tumia Equation\ ref {tanline1}.

\ (\ displaystyle\ kuanza {align*} m_ {tan} &=\ lim_ {x→ 3}\ frac {f (x) -f (3)} {x—3} &\ maandishi {Tumia ufafanuzi.}\\ [4pt]
&=\ lim_ {x→ 3}\ frac {x ^ 2—9} {x-1} & &\ maandishi {mbadala} {x^2,19} & &\ maandishi {f (x) =x ^ 2\ maandishi {na} f (3) =9\\ [4pt]
&=\ lim_ {x→ 3}\ frac {(x-3) (x+3)} {x-1 3} =\ lim_ {x→ 3} (x+3) =6 & ; &\ maandishi {Factor numerator kutathmini kikomo.} \ mwisho {align*}\)

Kisha, pata uhakika kwenye mstari wa tangent. Kwa kuwa mstari ni tangent kwa grafu ya$f(x)$ saa$x=3$, hupita kupitia hatua$(3,f(3))$. Tuna$f(3)=9$, hivyo mstari wa tangent hupita kupitia hatua$(3,9)$.

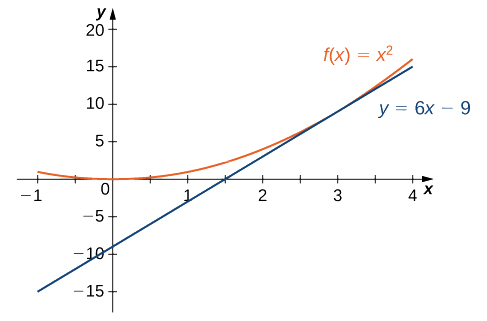
Kutumia equation ya mteremko wa mstari na mteremko$m=6$ na uhakika$(3,9)$, tunapata mstari$y−9=6(x−3)$. Kurahisisha, tuna$y=6x−9$. Grafu ya$f(x)=x^2$ na mstari wake wa tangent$3$ inavyoonekana kwenye Kielelezo$\PageIndex{5}$.

Takwimu hii ina grafu ya f (x) = x squared na y = 6x - 9. Grafu za kazi hizi zinaonekana kugusa saa x = 3. — Kielelezo$\PageIndex{5}$: line tangent kwa$f(x)$ saa$x=3$.

Mfano$\PageIndex{2}$: The Slope of a Tangent Line Revisited

Tumia Equation\ ref {tanline2} ili kupata mteremko wa mstari wa tangent kwenye grafu ya$f(x)=x^2$ saa$x=3$.

Suluhisho

Hatua ni sawa na Mfano$\PageIndex{1}$. Angalia Equation\ ref {tanline2} kwa ufafanuzi.

\ (\ kuanza {align*} m_ {tan} &=\ lim_ {h → 0}\ frac {f (3+h) -f (3)} {h} & &\ maandishi {Tumia ufafanuzi.}\\ [4pt]
&=\ lim_ {h → 0}\ frac {(3+h) ^2—9} {h} & &\ maandishi {mbadala} (f 3+h) =( 3+h) ^2\ maandishi {na} f (3) =9\\ [4pt]
&=\ lim_ {h → 0}\ frac {9+6h+h ^ 2,19} {h} & &\ maandishi {Panua na kurahisisha kutathmini kikomo.}\\ [4pt]
&=\ lim_ {h → 0}\ frac {h (6+h)} {h} =\ lim_ {h → 0} (6+h) =6\ mwisho {align*}\)

Tulipata thamani sawa kwa mteremko wa mstari wa tangent kwa kutumia ufafanuzi mwingine, kuonyesha kwamba kanuni zinaweza kubadilishana.

Mfano$\PageIndex{3}$: Finding the Equation of a Tangent Line

Kupata equation ya tangent line kwa grafu ya$f(x)=1/x$ saa$x=2$.

Suluhisho

Tunaweza kutumia Equation\ ref {tanline1}, lakini kama tulivyoona, matokeo ni sawa kama tunatumia Equation\ ref {tanline2}.

\ (\ displaystyle\ kuanza {align*} m_ {tan} &=\ lim_ {x→ 2}\ frac {f (x) -f (2)} {x-1} &\ maandishi {Tumia ufafanuzi.}\\ [4pt]
&=\ lim_ {x→ 2}\ frac {1} {x}\ frac {1} {x}\ frac {1}\ frac {1} {x}\ frac {1}\ frac {1} {x}\ frac {1}}} {x-1} & &\ maandishi {mbadala} f (x) =\ frac {1} {x}\ maandishi {na} f (2) =\ frac {1} {2}\ [4pt]
&=\ lim_ {x→ 2}\ frac {\ Frac {1} {x}}}\ frac {1} {2}} {x-2}}}\ Frac {2x} {2x} & &\ maandishi {Kuzidisha namba na denominator kwa} 2x\ maandishi {ili kurahisisha sehemu.}\\ [4pt]
&=\ lim_ {x→ 2}\ frac {(2ї x)} {(x-1)} {(x-1) (x-2) (2x)} & &\ maandishi {Kurahisisha.}\\ [4pt]
&=\ lim_ {x→ 2}\ frac {-1} {2x} & &\ maandishi {Kurahisisha kutumia}\ frac {2,1x} {x-1} =-1,\ maandishi {kwa} x2.\\ [4pt]
&=\\ frac {1} {4} & &\ maandishi {Tathmini kikomo.} \ mwisho {align*}\)

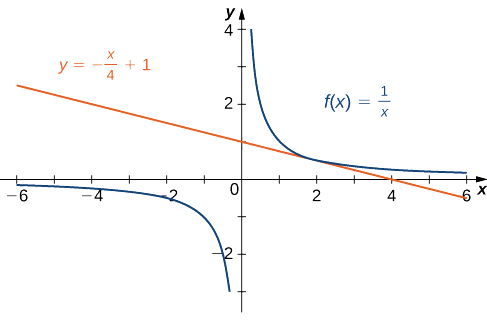
Sasa tunajua kwamba mteremko wa mstari wa tangent ni$−\frac{1}{4}$. Ili kupata equation ya mstari wa tangent, tunahitaji pia uhakika kwenye mstari. Tunajua kwamba$f(2)=\frac{1}{2}$. Kwa kuwa mstari wa tangent unapita kupitia hatua$(2,\frac{1}{2})$ tunaweza kutumia equation ya hatua-mteremko wa mstari ili kupata equation ya mstari wa tangent. Hivyo mstari wa tangent una equation$y=−\frac{1}{4}x+1$. Grafu za$f(x)=\frac{1}{x}$ na$y=−\frac{1}{4}x+1$ zinaonyeshwa kwenye Kielelezo$\PageIndex{6}$.

Takwimu hii ina grafu za f (x) = 1/x na y = -x/4 + 1. Sehemu ya grafu f (x) = 1/x katika quadrant ya kwanza inaonekana kugusa grafu ya kazi nyingine saa x = 2. — $\PageIndex{6}$Kielelezo:Mstari ni tangent kwa saa$f(x)$.$x=2$

Zoezi$\PageIndex{1}$

Pata mteremko wa mstari wa tangent kwenye grafu ya$f(x)=\sqrt{x}$ saa$x=4$.

Kidokezo: Tumia ama Equation\ ref {tanline1} au Equation\ ref {tanline2}. Panua namba na denominator kwa conjugate.

Jibu: $\frac{1}{4}$

Derivative ya Kazi katika Point

aina ya kikomo sisi kukokotoa ili kupata mteremko wa mstari tangent kwa kazi katika hatua hutokea katika maombi mengi katika taaluma nyingi. Maombi haya ni pamoja na kasi na kuongeza kasi katika fizikia, kazi pembezoni faida katika biashara, na viwango vya ukuaji katika biolojia. Kikomo hiki hutokea mara kwa mara kwamba tunatoa thamani hii jina maalum: derivative. Mchakato wa kutafuta derivative huitwa tofauti.

Ufafanuzi: derivative

Hebu$f(x)$ iwe kazi iliyoelezwa katika kipindi cha wazi kilicho na$a$. Derivative ya kazi$f(x)$ katika$a$, iliyoashiria na$f′(a)$, inaelezwa na

\[f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \label{der1} \]

zinazotolewa kikomo hii ipo.

Vinginevyo, tunaweza pia kufafanua derivative ya$f(x)$ saa$a$ kama

\[f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}. \label{der2} \]

Mfano$\PageIndex{4}$: Estimating a Derivative

Kwa$f(x)=x^2$, tumia meza ili kukadiria$f′(3)$ kutumia Equation\ ref {der1}.

Suluhisho

Unda meza kwa kutumia maadili$x$ ya chini$3$ na hapo juu$3$.

$x$	$\dfrac{x^2−9}{x−3}$
\ (x\)” style="text-align:katikati; "> 2.9	\ (\ dfrac {x^2,19} {x-3}\)” style="Nakala-align:katikati; "> 5.9
\ (x\)” style="text-align:katikati; "> 2.99	\ (\ dfrac {x^2,19} {x-3}\)” style="Nakala-align:katikati; "> 5.99
\ (x\)” style="Nakala-align:katikati; "> 2.999	\ (\ dfrac {x^2,19} {x,1-3}\)” style="Nakala-align:katikati; "> 5.999
\ (x\)” style="text-align:katikati; "> 3.001	\ (\ dfrac {x^2,19} {x-3}\)” style="Nakala-align:katikati; "> 6.001
\ (x\)” style="Nakala-align:katikati; "> 3.01	\ (\ dfrac {x^2,19} {x-3}\)” style="Nakala-align:katikati; "> 6.01
\ (x\)” style="text-align:katikati; "> 3.1	\ (\ dfrac {x^2,19} {x-3}\)” style="Nakala-align:katikati; "> 6.1

Baada ya kuchunguza meza, tunaona kwamba makadirio mazuri ni$f′(3)=6$.

Zoezi$\PageIndex{2}$

Kwa$f(x)=x^2$, kutumia meza kukadiria$f′(3)$ kutumia Equation\ ref {der2}.

Kidokezo: Tathmini$\dfrac{(x+h)^2−x^2}{h}$ katika$h=−0.1,\,−0.01,\,−0.001,\,0.001,\,0.01,\,0.1$

Jibu: 6

Mfano$\PageIndex{6}$: Finding a Derivative

Kwa$f(x)=3x^2−4x+1$, kupata$f′(2)$ kwa kutumia Equation\ ref {der1}.

Suluhisho

Badilisha kazi iliyotolewa na thamani moja kwa moja kwenye equation.

\ (\ displaystyle\ kuanza {align*} f′ (x) &=\ lim_ {x→ 2}\ frac {f (x) -f (2)} {x-1} &\ maandishi {Tumia ufafanuzi.}\\ [4pt]
&=\ lim_ {x→ 2}\ frac {(3x^2,14x+1) -5} {x-1} & &\ maandishi {mbadala} f (x) =3x^2,14x+1\ maandishi {na} f (2) =5.\\ [4pt]
&=\ lim_ {x→ 2}\ frac {(x-1) (3x+2)} {x-1} & amp;\ maandishi {Kurahisisha na sababu namba.}\\ [4pt]
&=\ lim_ {x→ 2} (3x+2) & &\ maandishi {Futa sababu ya kawaida.}\\ [4pt]
&=8 & &\ maandishi {Tathmini kikomo.} \ mwisho {align*}\)

Mfano$\PageIndex{7}$: Revisiting the Derivative

Kwa$f(x)=3x^2−4x+1$, kupata$f′(2)$ kwa kutumia Equation\ ref {der2}.

Suluhisho

Kutumia equation hii, tunaweza mbadala maadili mawili ya kazi katika equation, na tunapaswa kupata thamani sawa kama katika Mfano$\PageIndex{6}$.

\ (\ displaystyle\ kuanza {align*} f′ (2) &=\ lim_ {h → 0}\ frac {f (2+h) -f (2)} {h} &\ maandishi {Tumia ufafanuzi.}\\ [4pt]
&=\ lim_ {h → 0}\ frac {(3 (2+h) ^2,14 (2+h) +1) -5} {h} & &\ maandishi {mbadala} f (2) =5\ maandishi {na} f (2+h) =3 (2+h) ^2,14 (2+h) +1.\\ [4pt]
&=\ lim_ {h → 0}\ frac {3 (4+4h+h ^ 2) -8-4h+1-5} {h} & &\ maandishi {Panua nambari.}\\ [4pt]
&=\ lim_ {h → 0}\ frac {12+12h+3h ^ 2-12-4h} {h} & &\ maandishi {Kusambaza na kuanza kurahisisha nambari.}\\ [4pt]
&=\ lim_ {h → 0}\ frac {3h {3h+0}\ frac {3h+^ 2+8h} {h} & &\ maandishi {Kumaliza kurahisisha nambari.}\\ [4pt]
&=\ lim_ {h→ 0}\ frac {h (3h+8)} {h} & &\ maandishi {Kielelezo cha namba.}\\ [4pt]
&=\ lim_ {h → 0} (3h+8) &\ maandishi {Futa sababu ya kawaida.}\\ [4pt]
&=8 &\ maandishi {Tathmini kikomo.} \ mwisho {align*}\)

Matokeo ni sawa kama tunatumia Equation\ ref {der1} au Equation\ ref {der2}.

Zoezi$\PageIndex{4}$

Kwa$f(x)=x^2+3x+2$, kupata$f′(1)$.

Kidokezo: Tumia ama Equation\ ref {der1}, Equation\ ref {der2}, au jaribu zote mbili.

Jibu: $f′(1)=5$

Velocities na Viwango vya Mabadiliko

Sasa kwa kuwa tunaweza kutathmini derivative, tunaweza kutumia katika maombi ya kasi. Kumbuka kwamba ikiwa$s(t)$ ni nafasi ya kitu kinachohamia kando ya mhimili wa kuratibu, kasi ya wastani ya kitu juu ya muda wa muda$[a,t]$ ikiwa$t>a$ au$[t,a]$ ikiwa$t<a$ imetolewa na tofauti ya quotient

\[v_{ave}=\frac{s(t)−s(a)}{t−a}. \label{avgvel} \]

Kama maadili ya$t$ mbinu$a$, maadili ya$v_{ave}$ mbinu thamani tunayoita kasi ya papo hapo$a$. Hiyo ni, kasi ya instantaneous saa$a$, iliyoashiria$v(a)$, inatolewa na

\[v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}. \label{instvel} \]

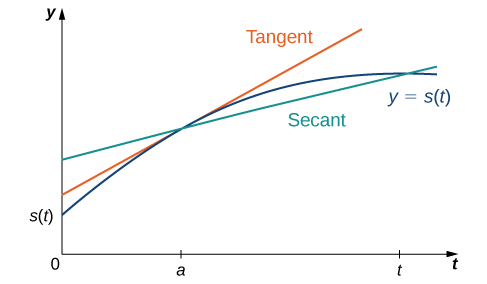
Ili kuelewa vizuri uhusiano kati ya kasi ya wastani na kasi ya haraka, angalia Kielelezo$\PageIndex{7}$. Katika takwimu hii, mteremko wa mstari wa tangent (umeonyeshwa kwa nyekundu) ni kasi ya papo hapo ya kitu wakati$t=a$ ambao nafasi yake kwa wakati$t$ hutolewa na kazi$s(t)$. Mteremko wa mstari wa salama (umeonyeshwa kwa kijani) ni kasi ya wastani ya kitu kwa muda wa muda$[a,t]$.

Takwimu hii ina ndege ya kuratibu ya Cartesian na 0, a, na t1 iliyowekwa kwenye mhimili wa t. Kazi y = s (t) ni graphed katika roboduara ya kwanza pamoja na mistari miwili alama tangent na secant. Mstari wa tangent unagusa y = s (t) kwa hatua moja tu, (a, s (a)). Mstari wa pili unagusa y = s (t) kwa pointi mbili: (a, s (a)) na (t1, s (t1)). — Kielelezo$\PageIndex{7}$: Mteremko wa mstari wa salama ni kasi ya wastani juu ya muda$[a,t]$. Mteremko wa mstari wa tangent ni kasi ya papo hapo.

Tunaweza kutumia Equation\ ref {instvel} kuhesabu kasi instantaneous, au tunaweza kukadiria kasi ya kitu kusonga kwa kutumia meza ya maadili. Tunaweza kisha kuthibitisha makadirio kwa kutumia Equation\ ref {avgvel}.

Mfano$\PageIndex{8}$: Estimating Velocity

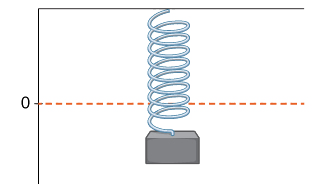
Uzito wa kuongoza juu ya chemchemi unasonga juu na chini. Msimamo wake$t$ kwa wakati kwa heshima ya mstari uliowekwa usawa hutolewa na$s(t)=\sin t$ (Kielelezo$\PageIndex{8}$). Tumia meza ya maadili kukadiria$v(0)$. Angalia makadirio kwa kutumia Equation\ ref {instvel}.

Picha ya spring kunyongwa chini na uzito mwishoni. Kuna mstari ulio na usawa uliowekwa alama 0 kidogo juu ya uzito. — Kielelezo$\PageIndex{8}$: uzito risasi kusimamishwa kutoka spring katika wima oscillatory mwendo.

Suluhisho

Tunaweza kukadiria kasi instantaneous katika$t=0$ kwa kompyuta meza ya kasi wastani kwa kutumia maadili ya$t$ inakaribia$0$, kama inavyoonekana katika Jedwali$\PageIndex{2}$.

Jedwali$\PageIndex{2}$: Wastani wa kasi kwa kutumia maadili ya$t$ inakaribia 0
$t$	$\frac{\sin t−\sin 0}{t−0}=\frac{\sin t}{t}$
\ (t\)” style="text-align:katikati; ">-0.1	\ (\ frac {\ sin t-1\ sin 0} {t-0} =\ frac {\ sin t} {t}\)” style="text-align:center; "> 0.998334166
\ (t\)” style="Nakala-align:katikati; "> -0.01	\ (\ frac {\ sin t-1\ sin 0} {t-0} =\ frac {\ sin t} {t}\)” style="text-align:center; "> 0.9999833333
\ (t\)” style="text-align:katikati; "> -0.001	\ (\ frac {\ sin t-1\ sin 0} {t-0} =\ frac {\ sin t} {t}\)” style="text-align:center; "> 0.999999833
\ (t\)” style="text-align:katikati; "> 0.001	\ (\ frac {\ sin t-1\ sin 0} {t-0} =\ frac {\ sin t} {t}\)” style="text-align:center; "> 0.999999833
\ (t\)” style="Nakala-align:katikati; "> 0.01	\ (\ frac {\ sin t-1\ sin 0} {t-0} =\ frac {\ sin t} {t}\)” style="text-align:center; "> 0.9999833333
\ (t\)” style="text-align:katikati; "> 0.1	\ (\ frac {\ sin t-1\ sin 0} {t-0} =\ frac {\ sin t} {t}\)” style="text-align:center; "> 0.998334166

Kutoka meza tunaona kwamba kasi ya wastani juu ya muda wa muda$[−0.1,0]$ ni$0.998334166$, kasi ya wastani juu ya muda wa muda$[−0.01,0]$ ni$0.9999833333$, na kadhalika. Kutumia meza hii ya maadili, inaonekana kwamba makadirio mazuri ni$v(0)=1$.

Kwa kutumia Equation\ ref {instvel}, tunaweza kuona kwamba

\[v(0)=s′(0)=\lim_{t→0}\frac{\sin t−\sin 0}{t−0}=\lim_{t→0}\frac{\sin t}{t}=1. \nonumber \]

Hivyo, kwa kweli,$v(0)=1$.

Zoezi$\PageIndex{5}$

Mwamba umeshuka kutoka urefu wa$64$ miguu. Urefu wake juu ya ardhi wakati$t$ sekunde baadaye hutolewa na$s(t)=−16t^2+64,\;0≤t≤2$. Kupata kasi yake instantaneous$1$ pili baada ya ni imeshuka, kwa kutumia Equation\ ref {instvel}.

Kidokezo: $v(t)=s′(t)$. Fuata mifano ya awali ya derivative kutumia Equation\ ref {instvel}.

Jibu: -32 ft/s

Kama tulivyoona katika sehemu hii, mteremko wa mstari tangent kwa kazi na kasi instantaneous ni dhana kuhusiana. Kila ni mahesabu kwa kompyuta derivative na kila hatua kiwango instantaneous ya mabadiliko ya kazi, au kiwango cha mabadiliko ya kazi wakati wowote pamoja kazi.

Ufafanuzi: Kiwango cha Mabadiliko ya papo hapo

Kiwango cha instantaneous cha mabadiliko ya kazi$f(x)$ kwa thamani$a$ ni derivative yake$f′(a)$.

Mfano$\PageIndex{9}$: Chapter Opener: Estimating Rate of Change of Velocity

Kufikia kasi ya juu ya$270.49$ mph, Hennessey Venom GT ni moja ya magari ya haraka zaidi duniani. Katika vipimo akaenda kutoka$0$ kwa$60$ mph katika$3.05$ sekunde, kutoka$0$ kwa$100$ mph katika$5.88$ sekunde, kutoka$0$ kwa$200$ mph katika$14.51$ sekunde, na kutoka$0$ kwa$229.9$ mph katika$19.96$ sekunde. Tumia data hii kuteka hitimisho kuhusu kiwango cha mabadiliko ya kasi (yaani, kuongeza kasi yake) kama inakaribia$229.9$ mph. Je! Kiwango ambacho gari linaharakisha kinaonekana kuongezeka, kupungua, au mara kwa mara?

Gari moja la michezo linaharakisha kando ya barabara inayozunguka tangu mwanzo wa sura. — Kielelezo$\PageIndex{9}$: (mikopo: mabadiliko ya kazi na Codex41, Flickr)

Solution: Kwanza kuchunguza kwamba$60$ mph =$88$$146.67$ ft/s,$200$ mph ≈$293.33$ ft/s,$229.9$ mph ≈$337.19$ ft/s, na mph ≈ ft/s.$100$

Jedwali$\PageIndex{3}$: $v(t)$ kwa maadili tofauti ya$t$
$t$	$v(t)$
\ (t\) "> 0	\ (v (t)\) "> 0
\ (t\) ">3.05	\ (v (t)\) "> 88
\ (t\) ">5.88	\ (v (t)\) ">147.67
\ (t\) ">14.51	\ (v (t)\) "> 293.33
\ (t\) ">19.96	\ (v (t)\) ">337.19

Sasa compute kasi ya wastani ya gari kwa miguu kwa pili juu ya vipindi vya fomu$[t,19.96]$ kama$t$ mbinu$19.96$, kama inavyoonekana katika meza ifuatayo.

Wastani wa kuongeza kasi
$t$	$\dfrac{v(t)−v(19.96)}{t−19.96}=\dfrac{v(t)−337.19}{t−19.96}$
\ (t\) "> 0.0	\ (\ dfrac {v (t) -v (19.96)} {t-19.96} =\ dfrac {v (t) -337.19} {t-19.96}\) ">16.89
\ (t\) ">3.05	\ (\ dfrac {v (t) -v (19.96)} {t-19.96} =\ dfrac {v (t) -337.19} {t-19.96}\) "> 14.74
\ (t\) ">5.88	\ (\ dfrac {v (t) -v (19.96)} {t-19.96} =\ dfrac {v (t) -337.19} {t-19.96}\) "> 13.46
\ (t\) ">14.51	\ (\ dfrac {v (t) -v (19.96)} {t-19.96} =\ dfrac {v (t) -337.19} {t-19.96}\) "> 8.05

Kiwango ambacho gari linaharakisha kinapungua kama kasi yake inakaribia$229.9$ mph ($337.19$ft/s).

Mfano$\PageIndex{10}$: Rate of Change of Temperature

Mmiliki wa nyumba anaweka thermostat ili joto ndani ya nyumba huanza kushuka kutoka$70°F$ saa$9$ p.m., kufikia chini ya$60°$ wakati wa usiku, na kuongezeka nyuma na.m. asubuhi iliyofuata.$70°$$7$ Tuseme kwamba joto ndani ya nyumba hutolewa na$T(t)=0.4t^2−4t+70$ kwa$0≤t≤10$, wapi idadi ya masaa$t$$9$ yaliyopita p.m. Pata kiwango cha instantaneous cha mabadiliko ya joto wakati wa usiku wa manane.

Suluhisho

Tangu usiku wa manane ni$3$ masaa iliyopita$9$ p.m., tunataka kukokotoa$T′(3)$. Rejea Equation\ ref {der1}.

\ (\ displaystyle\ kuanza {align*} T (3) &=\ lim_ {t → 3}\ frac {T (t) -T (3)} {t -3} &\ maandishi {Tumia ufafanuzi.}\\ [4pt]
&=\ lim_ {t → 3}\ frac {0.4t ^ 2,14t+70-61.6} {t-1 -3} & &\ maandishi {mbadala} T (t) =0.4t ^ 2,14t+70\ maandishi {na} T (3) =61.6.\\ [4pt]
&=\ lim_ {t→ 3}\ frac {0.4t ^ 2,14t+8.4} {t- 3} & &\ maandishi {Kurahisisha.}\\ [4pt]
&=\ lim_ {t → 3}\ Frac {0.4 (t-3) (t-7)} {t-3}\\ [4pt]
&=\ lim_ {t → 3} 0.4 (t-7) &\ maandishi {Futa.}\\ [4pt]
&=—1.6 &\ maandishi {Tathmini kikomo.} \ mwisho {align*}\)

Kiwango cha haraka cha mabadiliko ya joto wakati wa usiku wa manane ni$−1.6°F$ kwa saa.

Mfano$\PageIndex{11}$: Rate of Change of Profit

Kampuni ya toy inaweza kuuza mifumo ya michezo ya kubahatisha ya$x$ umeme kwa bei ya$p=−0.01x+400$ dola kwa mfumo wa michezo ya kubahatisha. Gharama ya$x$ mifumo ya viwanda hutolewa kwa$C(x)=100x+10,000$ dola. Kupata kiwango cha mabadiliko ya faida wakati$10,000$ michezo ni zinazozalishwa. Je, kampuni ya toy itaongeza au kupunguza uzalishaji?

Suluhisho

Faida$P(x)$ iliyopatikana kwa$x$ kuzalisha mifumo ya michezo ya kubahatisha$R(x)$ ni$R(x)−C(x)$, wapi mapato yaliyopatikana kutokana na uuzaji wa$x$ michezo. Kwa kuwa kampuni inaweza kuuza$x$ michezo kwa$p=−0.01x+400$ kila mchezo,

$R(x)=xp=x(−0.01x+400)=−0.01x^2+400x$.

Kwa hiyo,

$P(x)=−0.01x^2+300x−10,000$.

Kwa hiyo, kutathmini kiwango cha mabadiliko ya faida inatoa

\ (\ displaystyle\ kuanza {align*} P( 10000) &=\ lim_ {x → 10000}\ frac {P (x) -P (10000)} {x-10000}\\ [4pt]
&=\ lim_ {x→ 10000}\ frac {-0.01x^2+300x-10000-1990000} {x-10000}\\ [4pt]
&=\ lim_ {x→ 10000}\ frac {-0.01x^2+300x-2000000} {x-10000}\\ [4pt]
&=100\ mwisho {align*}\).

Tangu kiwango cha mabadiliko ya faida$P′(10,000)>0$ na$P(10,000)>0$, kampuni inapaswa kuongeza uzalishaji.

Zoezi$\PageIndex{6}$

kahawa huamua kwamba faida ya kila siku juu ya scones kupatikana kwa malipo ya dola s kwa scone ni$P(s)=−20s^2+150s−10$. duka kahawa sasa mashtaka$$3.25$ kwa kila scone. $P′(3.25)$Find, kiwango cha mabadiliko ya faida wakati bei ni$$3.25$ na kuamua kama au kahawa lazima kufikiria kuongeza au kupunguza bei yake juu ya scones.

Kidokezo: Matumizi Mfano$\PageIndex{11}$ kwa mwongozo.

Jibu: $P′(3.25)=20>0$; kuongeza bei

Dhana muhimu

Mteremko wa mstari wa tangent kwa pembe hupima kiwango cha instantaneous cha mabadiliko ya curve. Tunaweza kuhesabu kwa kutafuta kikomo cha quotient tofauti au quotient tofauti na increment$h$.
Derivative ya kazi$f(x)$ kwa thamani$a$ hupatikana kwa kutumia mojawapo ya ufafanuzi wa mteremko wa mstari wa tangent.
Velocity ni kiwango cha mabadiliko ya msimamo. Kwa hivyo, kasi kwa$v(t)$ wakati$t$ ni derivative ya nafasi$s(t)$ kwa wakati$t$.
Wastani wa kasi hutolewa kwa kasi\[v_{ave}=\dfrac{s(t)−s(a)}{t−a}. \nonumber \] instantaneous hutolewa na\[\displaystyle v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}. \nonumber \]
Tunaweza kukadiria derivative kwa kutumia meza ya maadili.

Mlinganyo muhimu

Tofauti quotient

$Q=\dfrac{f(x)−f(a)}{x−a}$

Tofauti quotient na nyongeza h

$Q=\dfrac{f(a+h)−f(a)}{a+h−a}=\dfrac{f(a+h)−f(a)}{h}$

Mteremko wa mstari wa tangent

$\displaystyle m_{tan}=\lim_{x→a}\frac{f(x)−f(a)}{x−a}$

$\displaystyle m_{tan}=\lim_{h→0}\frac{f(a+h)−f(a)}{h}$

Derivative ya f (x) katika

$\displaystyle f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a}$

$\displaystyle f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}$

Wastani wa kasi

$v_{ave}=\dfrac{s(t)−s(a)}{t−a}$

Kasi ya papo hapo

$\displaystyle v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}$

faharasa

derivative: mteremko wa mstari wa tangent kwa kazi kwa hatua, iliyohesabiwa kwa kuchukua kikomo cha quotient tofauti, ni derivative

tofauti quotient

ya kazi$f(x)$ katika$a$ ni iliyotolewa na

$\dfrac{f(a+h)−f(a)}{h}$au$\dfrac{f(x)−f(a)}{x−a}$

utofautishaji: mchakato wa kuchukua derivative

instantaneous kiwango cha mabadiliko: kiwango cha mabadiliko ya kazi wakati wowote pamoja na kazi$a$, pia inaitwa$f′(a)$, au derivative ya kazi katika$a$

Ufafanuzi: Tofauti Quotient

Ufafanuzi: Tangent Line

Mfano\(\PageIndex{1}\): Finding a Tangent Line

Mfano\(\PageIndex{2}\): The Slope of a Tangent Line Revisited

Mfano\(\PageIndex{3}\): Finding the Equation of a Tangent Line

Zoezi\(\PageIndex{1}\)

Ufafanuzi: derivative

Mfano\(\PageIndex{4}\): Estimating a Derivative

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{6}\): Finding a Derivative

Mfano\(\PageIndex{7}\): Revisiting the Derivative

Zoezi\(\PageIndex{4}\)

Mfano\(\PageIndex{8}\): Estimating Velocity

Zoezi\(\PageIndex{5}\)

Ufafanuzi: Kiwango cha Mabadiliko ya papo hapo

Mfano\(\PageIndex{9}\): Chapter Opener: Estimating Rate of Change of Velocity

Mfano\(\PageIndex{10}\): Rate of Change of Temperature

Mfano\(\PageIndex{11}\): Rate of Change of Profit

Zoezi\(\PageIndex{6}\)