2.1: Preview ya Calculus

Last updated
Save as PDF

Page ID: 178940

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Malengo ya kujifunza

Eleza tatizo la tangent na jinsi gani limesababisha wazo la derivative.
Eleza jinsi wazo la kikomo linahusika katika kutatua tatizo la tangent.
Kutambua tangent kwa Curve katika hatua kama kikomo ya mistari secant.
Kutambua kasi instantaneous kama kikomo cha kasi ya wastani juu ya muda mfupi wakati.
Eleza tatizo la eneo hilo na jinsi lilivyotatuliwa na muhimu.
Eleza jinsi wazo la kikomo linahusika katika kutatua tatizo la eneo hilo.
Kutambua jinsi mawazo ya kikomo, derivative, na muhimu imesababisha masomo ya mfululizo usio na kipimo na calculus multivariable.

Tunapoanza utafiti wetu wa calculus, tutaona jinsi maendeleo yake yalivyoondoka kutokana na ufumbuzi wa kawaida kwa matatizo ya vitendo katika maeneo kama vile uhandisi fizikia-kama tatizo la usafiri wa nafasi lililofanywa katika kopo la sura. Matatizo mawili muhimu yalisababisha uundaji wa awali wa calculus: (1) tatizo la tangent, au jinsi ya kuamua mteremko wa mstari wa tangent hadi kwenye hatua; na (2) tatizo la eneo, au jinsi ya kuamua eneo chini ya pembe.

Tatizo la Tangent na Calculus tofauti

Kiwango cha mabadiliko ni moja ya dhana muhimu zaidi katika calculus. Tunaanza uchunguzi wetu wa viwango vya mabadiliko kwa kuangalia grafu ya mistari mitatu\(f(x)=−2x−3,\; g(x)=\dfrac{1}{2}x+1\), na\(h(x)=2\), inavyoonekana kwenye Kielelezo\(\PageIndex{1}\).

Grafu tatu za mstari wa moja kwa moja. Moja, iliyoandikwa “f (x) = -2x - 3,” hupungua, kuvuka mhimili x saa -1.5 na mhimili y saa -3; mwingine, iliyoandikwa “g (x) = x/2 + 1,” huongezeka, kuvuka mhimili x saa -2 na mhimili y saa 1; ya tatu, iliyoandikwa “h (x) = 2,” ni gorofa katika y kuratibu 2 — Kielelezo\(\PageIndex{1}\): Kiwango cha mabadiliko ya kazi ya mstari ni mara kwa mara katika kila moja ya grafu hizi tatu, na mara kwa mara kuamua na mteremko.

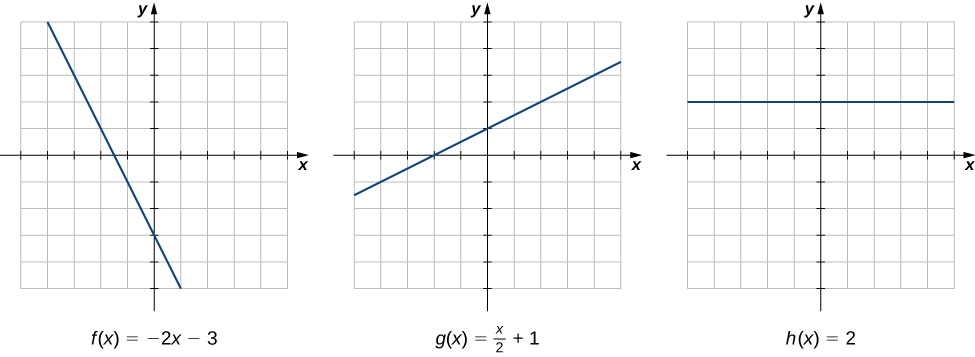
Kama sisi hoja kutoka kushoto kwenda kulia pamoja grafu ya\(f(x)=−2x−3\), tunaona kwamba graph itapungua kwa kiwango cha mara kwa mara. Kwa kila\(1\) kitengo tunahamia haki kando ya\(x\) -axis,\(y\) -kuratibu hupungua kwa\(2\) vitengo. Kiwango hiki cha mabadiliko kinatambuliwa na mteremko (\(−2\)) wa mstari. Vile vile, mteremko wa\(1/2\) kazi\(g(x)\) hutuambia kwamba kwa kila mabadiliko katika\(x\)\(1\) kitengo kuna mabadiliko yanayofanana katika\(y\) ya\(1/2\) kitengo. Kazi\(h(x)=2\) ina mteremko wa sifuri, kuonyesha kwamba maadili ya kazi hubakia mara kwa mara. Tunaona kwamba mteremko wa kila kazi ya mstari unaonyesha kiwango cha mabadiliko ya kazi.

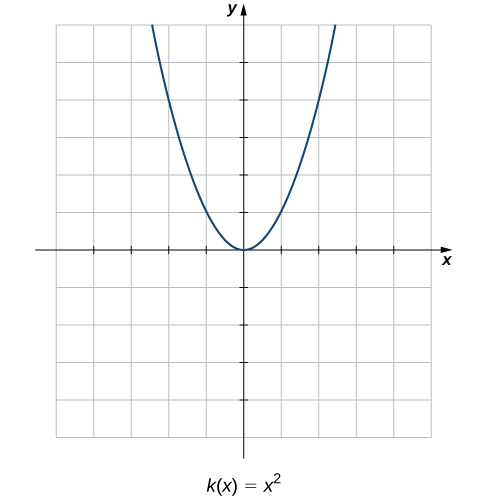
Linganisha grafu ya kazi hizi tatu na grafu ya\(k(x)=x^2\) (Kielelezo\(\PageIndex{2}\)). Grafu ya\(k(x)=x^2\) kuanza kutoka upande wa kushoto kwa kupungua kwa kasi, kisha huanza kupungua polepole zaidi na ngazi mbali, na kisha hatimaye huanza kuongeza-polepole mwanzoni, ikifuatiwa na kiwango cha ongezeko la ongezeko kama kinaendelea kuelekea kulia. Tofauti na kazi ya mstari, hakuna namba moja inawakilisha kiwango cha mabadiliko kwa kazi hii. Sisi kawaida kuuliza: Je, sisi kupima kiwango cha mabadiliko ya kazi nonlinear?

Grafu ya parabola k (x) = x ^ 2, ambayo inafungua na ina vertex yake katika asili. — Kielelezo\(\PageIndex{2}\): Kazi\(k(x)=x^2\) haina kiwango cha mabadiliko ya mara kwa mara.

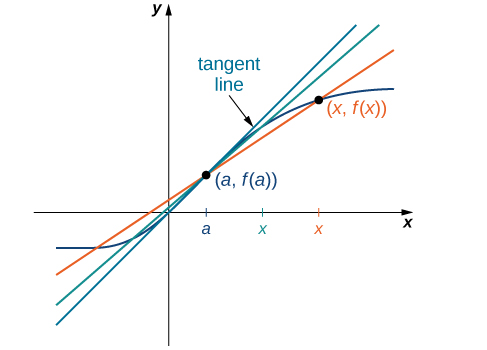
Tunaweza takriban kiwango cha mabadiliko ya kazi kwa\(f(x)\) hatua\((a,f(a))\) kwenye grafu yake kwa kuchukua hatua nyingine\((x,f(x))\) kwenye grafu ya\(f(x)\), kuchora mstari kupitia pointi mbili, na kuhesabu mteremko wa mstari unaosababisha. Mstari huo unaitwa mstari wa salama. Kielelezo\(\PageIndex{3}\) inaonyesha mstari secant kwa kazi\(f(x)\) katika hatua\((a,f(a))\).

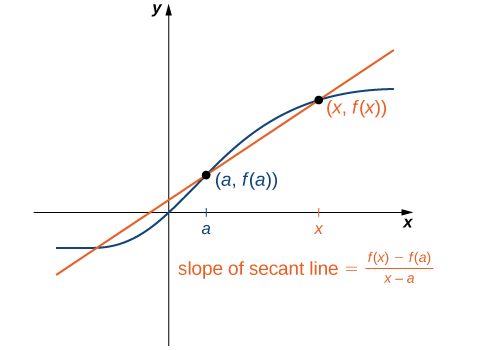
graph kuonyesha generic ikiwa kazi kupitia pointi (0,0), (a, fa.), na (x, f (x)). line moja kwa moja iitwayo line secant ni inayotolewa kwa njia ya pointi (a, fa.), na (x, f (x)), kwenda chini ya kazi ikiwa kati na x na kwenda juu ya kazi ikiwa katika maadili zaidi ya x au chini ya. kazi ikiwa na mstari secant msalaba mara moja zaidi katika baadhi ya hatua katika roboduara ya tatu. Mteremko wa mstari wa secant ni (f (x) — fa.)/(x — a). — Kielelezo\(\PageIndex{3}\): Mteremko wa mstari wa salama kwa njia ya hatua\((a,f(a))\) inakadiria kiwango cha mabadiliko ya kazi wakati huo\((a,f(a))\).

Sisi rasmi kufafanua mstari salama kama ifuatavyo:

Ufafanuzi: Secant Line

Sehemu ya kazi kwa\(f(x)\) njia ya pointi\((a,f(a))\) na\((x,f(x))\) ni mstari unaopita kupitia pointi hizi. Mteremko wake hutolewa na

\[m_{sec}=\dfrac{f(x)−f(a)}{x−a}. \label{secantslope} \]

Usahihi wa kukadiria kiwango cha mabadiliko ya kazi na mstari wa salama unategemea jinsi\(x\) ilivyo karibu\(a\). Kama tunavyoona katika Kielelezo\(\PageIndex{4}\)\(a\), ikiwa\(x\) ni karibu na, mteremko wa mstari wa salama ni kipimo bora cha kiwango cha mabadiliko ya\(f(x)\) saa\(a\).

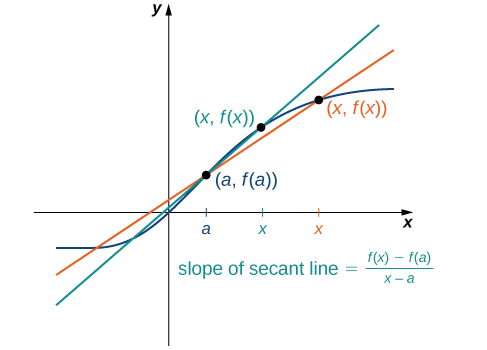
Grafu hii ni sawa na mstari uliopita wa secant na generic ikiwa kazi grafu. Hata hivyo, hatua nyingine x ni aliongeza, wakati huu walipanga karibu na juu ya x-axis. Kwa hivyo, mstari mwingine wa salama hutolewa kupitia pointi (a, fa.) na mpya, karibu (x, f (x)). line anakaa karibu sana na generic ikiwa kazi karibu (a, fa.). Mteremko wa mstari huu wa salama umekuwa makadirio bora ya kiwango cha mabadiliko ya kazi ya generic. — Kielelezo\(\PageIndex{4}\): Kama\(x\) inakaribia\(a\), mteremko wa mstari wa salama unakuwa makadirio bora kwa kiwango cha mabadiliko ya kazi\(f(x)\)\(a\).

Mstari wa secant wenyewe unakaribia mstari unaoitwa tangent\(f(x)\) kwa kazi\(a\) (Kielelezo\(\PageIndex{5}\)). Mteremko wa mstari wa tangent\(a\) kwenye grafu kwa kiwango cha mabadiliko ya kazi\(a\). Thamani hii pia inawakilisha derivative ya kazi\(f(x)\) katika\(a\), au kiwango cha mabadiliko ya kazi katika\(a\). Derivative hii inaashiria na\(f′(a)\). Calculus tofauti ni uwanja wa calculus unaohusika na utafiti wa derivatives na maombi yao.

Grafu hii ni kuendelea kwa mbili zilizopita. Wakati huu, grafu ina kazi iliyopigwa, mistari miwili ya salama, na mstari wa tangent. Kama x inakaribia a, mistari ya secant inakaribia mstari wa tangent. — Kielelezo\(\PageIndex{5}\): Kutatua Tatizo la Tangent: Kama\(x\) mbinu\(a\), mistari ya salama inakaribia mstari wa tangent.

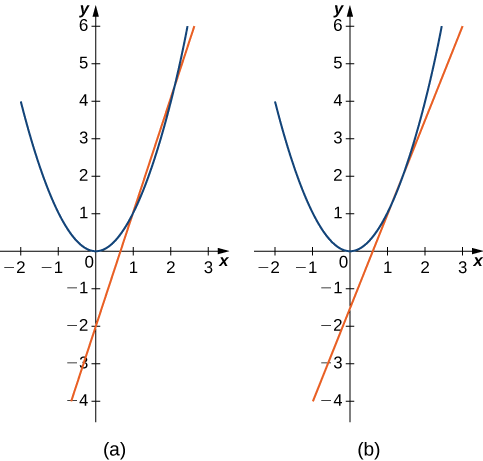
Mfano\(\PageIndex{1}\) unaeleza jinsi ya kupata mteremko wa mistari ya secant. Miteremko hii inakadiria mteremko wa mstari wa tangent au, sawa, kiwango cha mabadiliko ya kazi wakati ambapo mteremko huhesabiwa.

Mfano\(\PageIndex{1}\): Finding Slopes of Secant Lines

Tathmini ya mteremko wa mstari wa tangent (kiwango cha mabadiliko) kwa\(f(x)=x^2\) saa\(x=1\) kwa kutafuta mteremko wa mistari ya secant kupitia\((1,1)\) na kila moja ya pointi zifuatazo kwenye grafu ya\(f(x)=x^2\).

\((2,4)\)
\(\left(\dfrac{3}{2},\dfrac{9}{4}\right)\)

Suluhisho:

Tumia formula kwa mteremko wa mstari wa salama (Equation\ ref {secantslope}).

\(m_{sec}=\dfrac{4−1}{2−1}=3\)
\(m_{sec}=\dfrac{\dfrac{9}{4}−1}{\dfrac{3}{2}−1}=\dfrac{5}{2}=2.5\)

Hatua katika sehemu b. ni karibu na uhakika\((1,1)\), hivyo mteremko wa\(2.5\) ni karibu na mteremko wa mstari wa tangent. Makadirio mazuri ya mteremko wa tangent itakuwa katika kiwango cha\(2\) hadi\(2.5\) (Kielelezo\(\PageIndex{6}\)).

Grafu mbili za parabola f (x) = x ^ 2 zinaonyeshwa. Ya kwanza ina mstari wa secant inayotolewa, kuingiliana na parabola katika (1,1) na (2,4). Ya pili ina mstari wa secant inayotolewa, kuingiliana na parabola katika (1,1) na (3/2, 9/4). Mstari huu hutoa makadirio mfululizo karibu na mstari wa tangent kwa kazi katika (1,1). — Kielelezo\(\PageIndex{6}\): mistari secant kwa\(f(x)=x^2\)\((1,1)\) njia ya (a)\((2,4)\) na (b)\((\dfrac{3}{2},\dfrac{9}{4})\) kutoa makadirio mfululizo karibu na mstari tangent kwa\(f(x)=x^2\) saa\((1,1)\).

Zoezi\(\PageIndex{1}\)

Tathmini ya mteremko wa mstari wa tangent (kiwango cha mabadiliko) kwa\(f(x)=x^2\) saa\(x=1\) kwa kutafuta mteremko wa mistari ya secant kupitia\((1,1)\) na uhakika\((\dfrac{5}{4},\dfrac{25}{16})\) kwenye grafu ya\(f(x)=x^2\).

Jibu: \(2.25\)

Tunaendelea uchunguzi wetu kwa kuchunguza swali linalohusiana. Kuweka akilini kwamba kasi inaweza kuwa mawazo ya kama kiwango cha mabadiliko ya nafasi, tuseme kwamba tuna kazi\(s(t)\),, kwamba anatoa nafasi ya kitu pamoja kuratibu mhimili wakati wowote\(t\). Je, tunaweza kutumia mawazo haya sawa kujenga ufafanuzi busara wa kasi instantaneous kwa wakati fulani\(t=a?\) Tunaanza kwa kukadiria kasi instantaneous na kasi ya wastani. Kwanza, kumbuka kwamba kasi ya kitu kinachosafiri kwa kiwango cha mara kwa mara ni uwiano wa umbali uliosafiri hadi urefu wa muda uliosafiri. Tunafafanua kasi ya wastani ya kitu kwa kipindi cha muda kuwa mabadiliko katika msimamo wake umegawanyika na urefu wa kipindi cha wakati.

Ufafanuzi: Wastani wa kasi

Hebu\(s(t)\) kuwa nafasi ya kitu kusonga pamoja mhimili kuratibu kwa wakati\(t\). kasi ya wastani wa kitu juu ya muda wakati\([a,t]\) ambapo\(a<t\) (au\([t,a]\) kama\(t<a)\) ni

\[v_{ave}=\dfrac{s(t)−s(a)}{t−a}. \label{avgvel} \]

Kama\(t\) imechaguliwa karibu na\(a\), kasi ya wastani inakuwa karibu na kasi ya papo hapo. Kumbuka kuwa kutafuta kasi ya wastani wa kazi msimamo juu ya muda muda kimsingi ni sawa na kutafuta mteremko wa mstari secant kwa kazi. Zaidi ya hayo, ili kupata mteremko wa mstari wa tangent kwa hatua\(a\), tunaruhusu njia ya\(x\) maadili\(a\) katika mteremko wa mstari wa secant. Vile vile, ili kupata kasi ya papo hapo kwa wakati\(a\), tunaruhusu njia ya\(t\) maadili\(a\) kwa kasi ya wastani. Utaratibu huu wa kuruhusu\(x\) au\(t\) mbinu\(a\) katika kujieleza huitwa kuchukua kikomo. Hivyo, tunaweza kufafanua kasi instantaneous kama ifuatavyo.

Ufafanuzi: Upeo wa papo hapo

Kwa kazi ya msimamo\(s(t)\), kasi ya papo hapo kwa wakati\(t=a\) ni thamani ambayo kasi ya wastani inakaribia vipindi vya fomu\([a,t]\) na\([t,a]\) kama maadili ya\(t\) kuwa karibu na\(a\), ikiwa ni pamoja na thamani hiyo ipo.

Mfano\(\PageIndex{2}\) unaeleza dhana hii ya mipaka na kasi ya wastani.

Mfano\(\PageIndex{2}\): Finding Average Velocity

Mwamba umeshuka kutoka kimo cha futi 64. Imeamua kwamba urefu wake (kwa miguu) juu ya ardhi t sekunde baadaye (kwa\(0≤t≤2\)) hutolewa na\(s(t)=−16t^2+64\). Find kasi ya wastani wa mwamba juu ya kila moja ya vipindi kupewa wakati. Tumia habari hii kwa nadhani kasi instantaneous ya mwamba kwa wakati\(t=0.5\).

[\(0.49,0.5\)]
[\(0.5,0.51\)]

Suluhisho

Badilisha data katika Equation\ ref {avgvel} kwa ufafanuzi wa kasi ya wastani.

\[v_{ave}=\dfrac{s(0.49)−s(0.5)}{0.49−0.5}=−15.84 \nonumber \]
\[v_{ave}=\dfrac{s(0.51)−s(0.5)}{0.51−0.5}=−16.016 \nonumber \]

Kasi ya papo hapo ni mahali fulani kati ya -15.84 na -16.16 ft/sec. Nadhani nzuri huenda -16 ft/sec.

Zoezi\(\PageIndex{2}\)

Kitu kinachotembea kando ya mhimili wa kuratibu ili msimamo wake\(t\) kwa wakati utolewe na\(s(t)=t^3\). Tathmini kasi yake instantaneous\(t=2\) kwa wakati kwa kompyuta kasi yake wastani juu ya muda wa muda [\(2,2.001\)].

Kidokezo: Matumizi Equation\ ref {avgvel} kwa\(v_{ave}=\dfrac{s(2.001)−s(2)}{2.001−2}\).

Jibu: 12.006001

Tatizo la Eneo na Calculus Integral

Sasa tunageuka mawazo yetu kwa swali la classic kutoka kwa calculus. Wengi wingi katika fizikia-kwa mfano, kiasi cha kazi-inaweza kutafsiriwa kama eneo chini ya Curve. Hii inatuongoza kuuliza swali: Tunawezaje kupata eneo kati ya grafu ya kazi na\(x\) -axis juu ya muda (Kielelezo\(\PageIndex{7}\))?

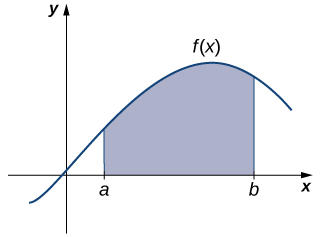
Grafu inavyoonekana ya kazi ya generic ikiwa f (x) umbo kama kilima katika roboduara moja. Eneo chini ya kazi ni kivuli juu ya x-axis na kati ya x=a na x=b. — Kielelezo\(\PageIndex{7}\): Tatizo la Eneo: Tunawezaje kupata eneo la eneo la kivuli?

Kama ilivyo katika jibu la maswali yetu ya awali juu ya kasi, sisi kwanza tunajaribu takriban suluhisho. Tunakaribia eneo hilo kwa kugawanya muda\([a,b]\) katika vipindi vidogo katika sura ya rectangles. Ukadiriaji wa eneo hilo unatoka kwa kuongeza maeneo ya rectangles hizi (Kielelezo\(\PageIndex{8}\)).

Grafu ni sawa na picha ya awali, na tofauti moja. Badala ya eneo hilo limevuliwa kabisa chini ya kazi ya pembe, muda [a, b] umegawanywa katika vipindi vidogo katika sura ya mstatili. Mstatili una upana mdogo sawa. Urefu wa kila mstatili ni urefu wa kazi katikati ya msingi wa mstatili maalum. — Kielelezo\(\PageIndex{8}\): Eneo la kanda chini ya pembe ni takriban kwa kuhesabu maeneo ya rectangles nyembamba.

Kama upana wa rectangles kuwa ndogo (mbinu sifuri), jumla ya maeneo ya rectangles inakaribia eneo kati ya grafu\(f(x)\) na\(x\) -axis juu ya muda\([a,b]\). Mara nyingine tena, tunajikuta kuchukua kikomo. Mipaka ya aina hii hutumika kama msingi wa ufafanuzi wa muhimu. Calculus Integral ni utafiti wa integrals na maombi yao.

Mfano\(\PageIndex{3}\): Estimation Using Rectangles

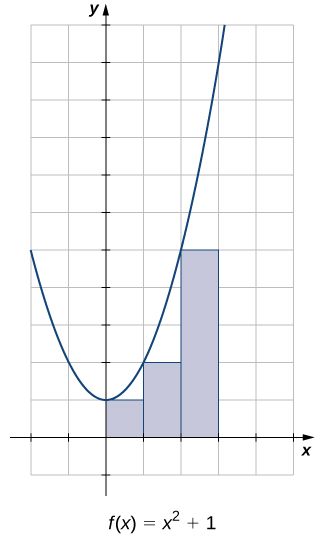
Tathmini eneo kati ya\(x\) -axis na grafu ya\(f(x)=x^2+1\) zaidi ya muda\([0,3]\) kwa kutumia rectangles tatu inavyoonekana katika Kielelezo\(\PageIndex{9}\).

Grafu ya parabola kufungua zaidi na hatua ya chini kabisa katika (0,1). Mstatili wa urefu 1 unaoenea kutoka x=0 hadi x=1 unagusa parabola kwenye hatua (0,1); mstatili wa urefu 2 kutoka x=1 hadi x=2 huigusa kwa uhakika (1,2); mstatili wa urefu 5 kutoka x=2 hadi x=3 huigusa kwa uhakika (2,5) — Kielelezo\(\PageIndex{9}\): Eneo la kanda chini ya pembe ya\(f(x)=x^2+1\) inaweza kuhesabiwa kwa kutumia rectangles.

Suluhisho

Maeneo ya rectangles tatu ni 1 kitengo ², 2 kitengo ², na 5 kitengo ². Kutumia rectangles hizi, makadirio yetu ya eneo ni 8 kitengo ².

Zoezi\(\PageIndex{3}\)

Tathmini eneo kati ya\(x\) -axis na grafu ya\(f(x)=x^2+1\) zaidi ya muda\([0,3]\) kwa kutumia rectangles tatu inavyoonekana katika Kielelezo\(\PageIndex{10}\).

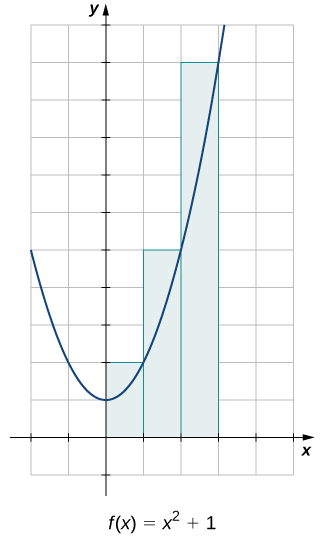
Grafu ya parabola kufungua zaidi, na hatua yake ya chini kabisa katika hatua (0,1). Mstatili wa urefu wa 2 na kupanua kutoka x=0 hadi x=1 hugusa parabola kwenye hatua (1,2); mstatili wa urefu 5 kutoka x=1 hadi x=2 huigusa kwa uhakika (2,5); mstatili wa urefu 10 kutoka x=2 hadi x=3 huigusa kwa uhakika (3,10) — Kielelezo\(\PageIndex{10}\): Eneo la kanda chini ya pembe ya\(f(x)=x^2+1\) inaweza kuhesabiwa kwa kutumia rectangles.

Kidokezo: Tumia Mfano\(\PageIndex{3}\) kama mwongozo

Jibu: 17\(\mathrm{unit}^2\)

Mambo mengine ya Calculus

Hadi sasa, tuna alisoma kazi ya variable moja tu. Kazi hizo zinaweza kuwakilishwa kwa kutumia grafu kwa vipimo viwili; hata hivyo, hakuna sababu nzuri ya kuzuia uchunguzi wetu kwa vipimo viwili. Tuseme, kwa mfano, kwamba badala ya kuamua kasi ya kitu kinachohamia kando ya mhimili wa kuratibu, tunataka kuamua kasi ya mwamba iliyotokana na manati kwa wakati fulani, au ya ndege inayohamia kwa vipimo vitatu. Tunaweza kutaka graph kazi halisi ya thamani ya vigezo mbili au kuamua kiasi cha yabisi ya aina inavyoonekana katika Kielelezo\(\PageIndex{11}\). Hizi ni chache tu ya aina ya maswali ambayo yanaweza kuulizwa na kujibiwa kwa kutumia calculus multivariable. Kwa kawaida, calculus multivariable inaweza kuwa kama utafiti wa calculus ya kazi ya vigezo mbili au zaidi. Hata hivyo, kabla ya kuchunguza mawazo haya na mengine, lazima kwanza kuweka msingi wa utafiti wa calculus katika variable moja kwa kuchunguza dhana ya kikomo.

Mchoro katika nafasi tatu za mwelekeo, juu ya x, y, na z mhimili ambapo z = f (x, y). Msingi ni mhimili wa x, y, na urefu ni mhimili wa z. Msingi ni mstatili ulio na ndege ya mhimili wa x, y. Juu ni uso wa urefu wa kubadilisha na pembe ziko moja kwa moja juu ya zile za mstatili katika ndege ya x, y.. Sehemu ya juu iko juu ya kona katika x=0, y=0. Hatua ya chini kabisa iko kwenye kona mahali fulani katika quadrant ya kwanza ya ndege ya x, y. Vipengele vingine viwili ni takribani urefu sawa na ziko juu ya pembe kwenye mhimili x na y mhimili. Mistari hutolewa kuunganisha pembe za mstatili kwa wale wa uso. — Kielelezo\(\PageIndex{11}\): Tunaweza kutumia calculus multivariable kupata kiasi kati ya uso inavyoelezwa na kazi ya vigezo mbili na ndege.

Dhana muhimu

Calculus tofauti iliondoka kutokana na kujaribu kutatua tatizo la kuamua mteremko wa mstari wa tangent kwa pembe kwa hatua. Mteremko wa mstari wa tangent unaonyesha kiwango cha mabadiliko ya kazi, pia huitwa derivative. Kuhesabu derivative inahitaji kupata kikomo.
Calculus Integral iliondoka kwa kujaribu kutatua tatizo la kutafuta eneo la kanda kati ya grafu ya kazi na\(x\) -axis. Tunaweza kulinganisha eneo hilo kwa kugawanya katika rectangles nyembamba na kuhesabu maeneo ya rectangles hizi. Summation hii inaongoza kwa thamani ya kazi inayoitwa muhimu. Muhimu pia huhesabiwa kwa kutafuta kikomo na, kwa kweli, ni kuhusiana na derivative ya kazi.
Calculus multivariable inatuwezesha kutatua matatizo katika nafasi tatu-dimensional, ikiwa ni pamoja na kuamua mwendo katika nafasi na kutafuta kiasi cha yabisi.

Mlinganyo muhimu

Mteremko wa Mstari wa Secant

\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)

Wastani wa kasi juu ya Muda [a, t]

\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)

faharasa

kasi ya wastani: mabadiliko katika nafasi ya kitu imegawanywa na urefu wa kipindi cha muda; kasi ya wastani ya kitu juu ya muda wa muda [\(t,a\)] (kama\(t<a\) au [\(a,t\)] kama\(t>a\)), na nafasi iliyotolewa na\(s(t)\), yaani\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)

calculus tofauti: uwanja wa calculus wasiwasi na utafiti wa derivatives na maombi yao

kasi ya papo hapo: Kasi ya papo hapo ya kitu kilicho na kazi ya msimamo ambayo hutolewa na\(s(t)\) ni thamani ambayo kasi ya wastani juu ya vipindi vya fomu [\(t,a\)\(a,t\)] na [] mbinu kama maadili ya\(t\) hoja karibu na\(a\), mradi thamani hiyo ipo

calculus muhimu: utafiti wa integrals na maombi yao

kikomo: mchakato wa kuruhusu x au t mbinu katika kujieleza; kikomo cha kazi\(f(x)\) kama\(x\) mbinu\(a\) ni thamani ambayo\(f(x)\) inakaribia kama\(x\) mbinu\(a\)

calculus multivariable: utafiti wa calculus ya kazi ya vigezo mbili au zaidi

sehemu: Mstari wa secant kwa kazi\(f(x)\) katika\(a\) ni mstari kupitia hatua (\(a,f(a)\)) na hatua nyingine juu ya kazi; mteremko wa mstari wa secant hutolewa na\(m_{sec}=\dfrac{f(x)−f(a)}{x−a}\)

tangent: mstari tangent kwa grafu ya kazi katika hatua (\(a,f(a)\)) ni mstari kwamba secant mistari kupitia (\(a,f(a)\)) mbinu kama wao ni kuchukuliwa kwa njia ya pointi juu ya kazi na\(x\) -maadili kwamba mbinu\(a\); mteremko wa mstari tangent kwa grafu katika\(a\) hatua ya kiwango cha mabadiliko ya kazi katika\(a\)