Skip to main content
Global

11.5E: Mazoezi

  1. Last updated
  2. Save as PDF
  • Page ID
    176866

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Mazoezi hufanya kamili

    Zoezi\(\PageIndex{13}\) Graph a Hyperbola with Center at \((0,0)\)

    Katika mazoezi yafuatayo, grafu.

    1. \(\frac{x^{2}}{9}-\frac{y^{2}}{4}=1\)
    2. \(\frac{x^{2}}{25}-\frac{y^{2}}{9}=1\)
    3. \(\frac{x^{2}}{16}-\frac{y^{2}}{25}=1\)
    4. \(\frac{x^{2}}{9}-\frac{y^{2}}{36}=1\)
    5. \(\frac{y^{2}}{25}-\frac{x^{2}}{4}=1\)
    6. \(\frac{y^{2}}{36}-\frac{x^{2}}{16}=1\)
    7. \(16 y^{2}-9 x^{2}=144\)
    8. \(25 y^{2}-9 x^{2}=225\)
    9. \(4 y^{2}-9 x^{2}=36\)
    10. \(16 y^{2}-25 x^{2}=400\)
    11. \(4 x^{2}-16 y^{2}=64\)
    12. \(9 x^{2}-4 y^{2}=36\)
    Jibu

    1.

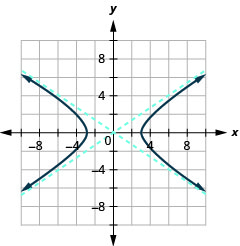
    Grafu inaonyesha x-axis na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya, lakini katika vipindi unlabeled, na asymptotes y ni sawa na plus au bala mara theluthi mbili x, na matawi ambayo hupitia vertices (pamoja au chini ya 3, 0) na kufungua kushoto na kulia.
    Kielelezo 11.4.33

    3.

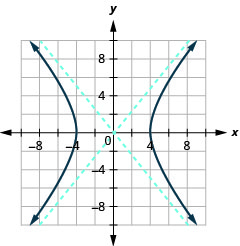
    Grafu inaonyesha x-axis na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na asymptotes y ni sawa na pamoja au minus mara nne x, na matawi ambayo hupitia vertices (pamoja au minus 4, 0) na kufungua kushoto na kulia.
    Kielelezo 11.4.34

    5.

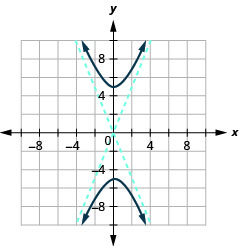
    Grafu inaonyesha x-axis na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na asymptotes y ni sawa na pamoja au minus nusu tano mara x, na matawi ambayo hupita kupitia vipeo (0, pamoja au minus 5) na kufungua juu na chini.
    Kielelezo 11.4.35

    7.

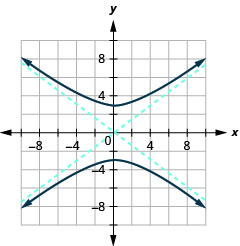
    Grafu inaonyesha x-axis na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na asymptotes y ni sawa na pamoja au minus mara tatu ya nne x, na matawi ambayo hupitia vertices (0, pamoja au minus 3) na kufungua juu na chini.
    Kielelezo 11.4.36

    9.

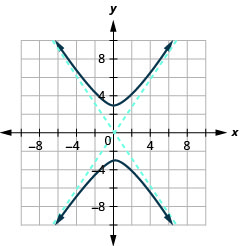
    Grafu inaonyesha x-axis na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na asymptotes y ni sawa na pamoja au minus mara nusu tatu x, na matawi ambayo hupita kupitia vipeo (0, pamoja au minus 3) na kufungua juu na chini.
    Kielelezo 11.4.37

    11.

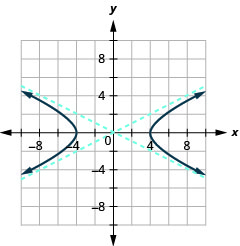
    Grafu inaonyesha x-axis na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na asymptotes y ni sawa na pamoja au minus mara nusu x, na matawi ambayo hupita kupitia vipeo (pamoja au minus 4, 0) na kufungua kushoto na kulia.
    Kielelezo 11.4.38
    Zoezi\(\PageIndex{14}\) Graph a Hyperbola with Center at \((h,k)\)

    Katika mazoezi yafuatayo, grafu.

    1. \(\frac{(x-1)^{2}}{16}-\frac{(y-3)^{2}}{4}=1\)
    2. \(\frac{(x-2)^{2}}{4}-\frac{(y-3)^{2}}{16}=1\)
    3. \(\frac{(y-4)^{2}}{9}-\frac{(x-2)^{2}}{25}=1\)
    4. \(\frac{(y-1)^{2}}{25}-\frac{(x-4)^{2}}{16}=1\)
    5. \(\frac{(y+4)^{2}}{25}-\frac{(x+1)^{2}}{36}=1\)
    6. \(\frac{(y+1)^{2}}{16}-\frac{(x+1)^{2}}{4}=1\)
    7. \(\frac{(y-4)^{2}}{16}-\frac{(x+1)^{2}}{25}=1\)
    8. \(\frac{(y+3)^{2}}{16}-\frac{(x-3)^{2}}{36}=1\)
    9. \(\frac{(x-3)^{2}}{25}-\frac{(y+2)^{2}}{9}=1\)
    10. \(\frac{(x+2)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
    Jibu

    1.

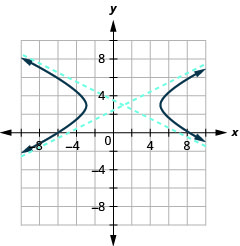
    Grafu inaonyesha x-mhimili na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na kituo cha (1, 3) asymptote ambayo hupitia (hasi 3, 1) na (5, 5) na asymptote ambayo hupitia (5, 1) na (hasi 3, 5), na matawi ambayo hupitia vipeo (hasi 3, 3) na (5, 3) na kufungua kushoto na kulia.
    Kielelezo 11.4.39

    3.

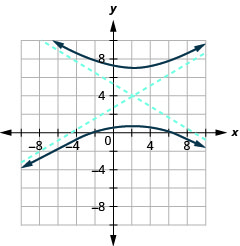
    Grafu inaonyesha x-mhimili na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na kituo cha (1, 3) asymptote ambayo hupitia (hasi 3, 1) na (5, 5) na asymptote ambayo hupitia (5, 1) na (hasi 3, 5), na matawi ambayo hupitia vipeo (hasi 3, 3) na (5, 3) na kufungua kushoto na kulia.
    Kielelezo 11.4.40

    5.

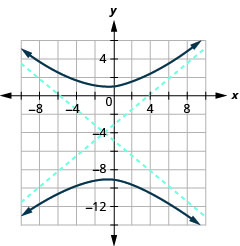
    Grafu inaonyesha x-mhimili na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na kituo cha (1, hasi 4) asymptote ambayo hupitia (hasi 7, 1) na (5, hasi 9) na asymptote ambayo hupita kupitia (5, 1) na (hasi 7, hasi 9), na matawi ambayo hupitia vertices (1, 1) na (1, hasi 9) na kufungua juu na chini.
    Kielelezo 11.4.41

    7.

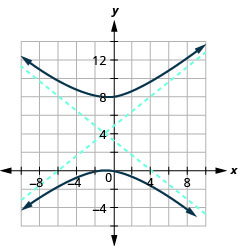
    Grafu inaonyesha x-mhimili na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na kituo cha (hasi 1, 4) asymptote ambayo hupitia (4, 8) na (hasi 6, 0) na asymptote ambayo hupitia (hasi 6, 8) na (4, 0), na matawi ambayo hupitia vipeo (hasi 1, 0) na ( hasi 1, 8) na kufungua juu na chini.
    Kielelezo 11.4.42

    9.

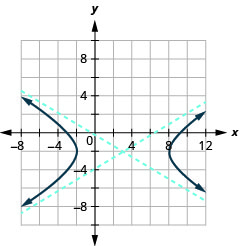
    Grafu inaonyesha x-axis na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na kituo cha (3, hasi 2) asymptote ambayo hupitia (8, 1) na (hasi 2, hasi 5) na asymptote ambayo hupita kupitia (hasi 2, hasi 1) na (8, hasi 5), na matawi ambayo hupita vertices (hasi 2, hasi 2) na (8, hasi 2) na kufungua kushoto na kulia.
    Kielelezo 11.4.43
    Zoezi\(\PageIndex{15}\) Graph a Hyperbola with Center at \((h,k)\)

    Katika mazoezi yafuatayo,

    1. Andika equation katika fomu ya kawaida na
    2. Grafu.
    1. \(9 x^{2}-4 y^{2}-18 x+8 y-31=0\)
    2. \(16 x^{2}-4 y^{2}+64 x-24 y-36=0\)
    3. \(y^{2}-x^{2}-4 y+2 x-6=0\)
    4. \(4 y^{2}-16 x^{2}-24 y+96 x-172=0\)
    5. \(9 y^{2}-x^{2}+18 y-4 x-4=0\)
    Jibu

    1.

    1. \(\frac{(x-1)^{2}}{4}-\frac{(y-1)^{2}}{9}=1\)
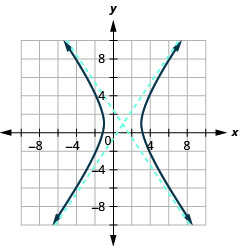
    Grafu inaonyesha x-mhimili na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na kituo cha (1, 1) asymptote ambayo hupitia (3, 4) na (hasi 1, hasi 2) na asymptote ambayo hupita kupitia (hasi 1, 4) na (3, hasi 2), na matawi ambayo hupitia vertices (hasi 1, 1) na (3, 1) na kufungua kushoto na kulia.
    Kielelezo 11.4.44

    3.

    1. \(\frac{(y-2)^{2}}{9}-\frac{(x-1)^{2}}{9}=1\)
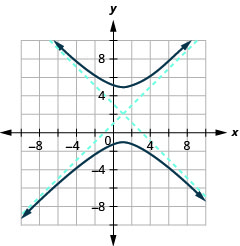
    Grafu inaonyesha x-axis na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na kituo cha (1, 2) asymptote ambayo hupitia (4, 5) na (hasi 2, hasi 1) na asymptote ambayo hupitia (hasi 2, 5) na (4, hasi 1), na matawi ambayo hupitia vertices (1, 5) na ( 1, hasi 1) na kufungua juu na chini.
    Kielelezo 11.4.45

    5.

    1. \(\frac{(y+1)^{2}}{1}-\frac{(x+2)^{2}}{9}=1\)
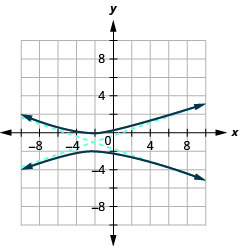
    Grafu inaonyesha x-axis na y-mhimili kwamba wote kukimbia katika mwelekeo hasi na chanya na kituo cha (hasi 2, hasi 1) asymptote ambayo hupitia (1, 0) na (hasi 5, hasi 2) na asymptote ambayo hupita kupitia (3, 0) na (1, hasi 2), na matawi ambayo hupita kupitia vertices ( hasi 2, 0) na (hasi 2, hasi 2) na kufungua juu na chini.
    Kielelezo 11.4.46
    Zoezi\(\PageIndex{16}\) Identify the Graph of each Equation as a Circle, Parabola, Ellipse, or Hyperbola

    Katika mazoezi yafuatayo, tambua aina ya grafu.

      1. \(x=-y^{2}-2 y+3\)
      2. \(9 y^{2}-x^{2}+18 y-4 x-4=0\)
      3. \(9 x^{2}+25 y^{2}=225\)
      4. \(x^{2}+y^{2}-4 x+10 y-7=0\)
      1. \(x=-2 y^{2}-12 y-16\)
      2. \(x^{2}+y^{2}=9\)
      3. \(16 x^{2}-4 y^{2}+64 x-24 y-36=0\)
      4. \(16 x^{2}+36 y^{2}=576\)
    Jibu

    2.

    1. Parabola
    2. Circle
    3. Hyperbola
    4. duaradufu
    Zoezi\(\PageIndex{17}\) Mixed Practice

    Katika mazoezi yafuatayo, graph kila equation.

    1. \(\frac{(y-3)^{2}}{9}-\frac{(x+2)^{2}}{16}=1\)
    2. \(x^{2}+y^{2}-4 x+10 y-7=0\)
    3. \(y=(x-1)^{2}+2\)
    4. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    5. \((x+2)^{2}+(y-5)^{2}=4\)
    6. \(9 x^{2}-4 y^{2}+54 x+8 y+41=0\)
    7. \(x=-y^{2}-2 y+3\)
    8. \(16 x^{2}+9 y^{2}=144\)
    Jibu

    2.

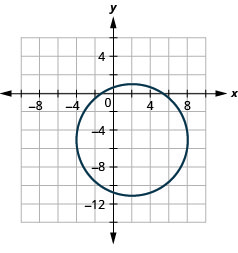
    Grafu inaonyesha ndege ya kuratibu x y na mduara ambao kituo chake ni (2, hasi 5) na ambao radius ni vitengo 6.
    Kielelezo 11.4.47

    4.

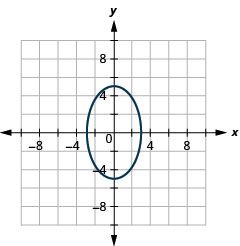
    Grafu inaonyesha ndege ya kuratibu x y na duaradufu ambao mhimili mkubwa ni wima, vipeo ni (0, pamoja au chini ya 5) na vyeo vya ushirikiano ni (pamoja au chini ya 3, 0).
    Kielelezo 11.4.48

    6.

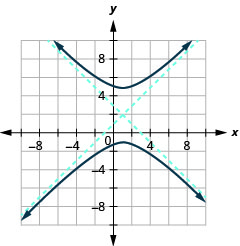
    Grafu inaonyesha x y kuratibu ndege na kituo cha (1, 2) asymptote ambayo hupitia (hasi 2, 5) na (5, hasi 1) na asymptote ambayo hupitia (4, 5) na (2, 0), na matawi ambayo hupitia vipeo (1, 5) na (hasi 2, hasi 1) na kufungua juu na chini.
    Kielelezo 11.4.49

    8.

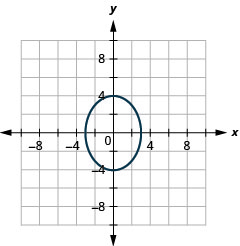
    Grafu inaonyesha x y kuratibu ndege na duaradufu ambayo mhimili kuu ni wima, vipeo ni (0, pamoja au minus 4) na ushirikiano vertices ni (pamoja au minus 3, 0).
    Kielelezo 11.4.50
    Zoezi\(\PageIndex{18}\) Writing Exercises
    1. Kwa maneno yako mwenyewe, fafanua hyperbola na uandike usawa wa hyperbola unaozingatia asili katika fomu ya kawaida. Chora mchoro wa hyperbola kuipatia kituo, vertices, na asymptotes.
    2. Eleza kwa maneno yako mwenyewe jinsi ya kuunda na kutumia mstatili unaosaidia grafu hyperbola.
    3. Linganisha na kulinganisha grafu ya equations\(\frac{x^{2}}{4}-\frac{y^{2}}{9}=1\) na\(\frac{y^{2}}{9}-\frac{x^{2}}{4}=1\).
    4. Eleza kwa maneno yako mwenyewe, jinsi ya kutofautisha equation ya ellipse na equation ya hyperbola.
    Jibu

    2. Majibu inaweza kutofautiana

    4. Majibu inaweza kutofautiana

    Self Check

    Baada ya kukamilisha mazoezi, tumia orodha hii ili kutathmini ujuzi wako wa malengo ya sehemu hii.

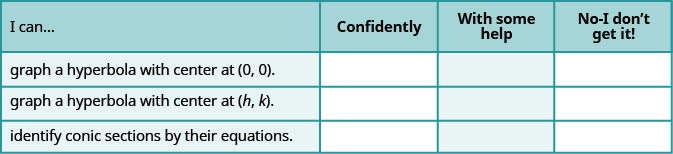
    Jedwali hili lina nguzo nne na safu nne. Mstari wa kwanza ni kichwa na inaandika kila safu, â € can â € €, â € kwa ujasiri, â € € â € kwa msaada fulani, â € na â € no-i donâ €™ t kupata! â € Katika mstari wa 2, naweza mara graph hyperbola na kituo cha saa (0, 0). Katika mstari wa 3, naweza mara graph hyperbola na kituo cha saa (h, k). mfululizo 4, naweza mara kutambua sehemu conic na equations yao.
    Kielelezo 11.4.51

    b Kwa kiwango cha 1-10, ungewezaje kupima ujuzi wako wa sehemu hii kwa kuzingatia majibu yako kwenye orodha? Unawezaje kuboresha hii?