Home
Kiswahili
Algebra ya kati (OpenStax)
11: Conics
11.6: Kutatua Mifumo ya Equations Nonlinear

11.6: Kutatua Mifumo ya Equations Nonlinear

Last updated
Save as PDF

Page ID: 176826

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Malengo ya kujifunza

Mwishoni mwa sehemu hii, utaweza:

Tatua mfumo wa equations isiyo ya kawaida kwa kutumia graphing
Kutatua mfumo wa equations nonlinear kwa kutumia mbadala
Kutatua mfumo wa equations nonlinear kwa kutumia kuondoa
Tumia mfumo wa equations nonlinear kutatua maombi

Kabla ya kuanza, fanya jaribio hili la utayari.

Tatua mfumo kwa kuchora:$\left\{\begin{array}{l}{x-3 y=-3} \\ {x+y=5}\end{array}\right.$.
Kama amekosa tatizo hili, mapitio Mfano 4.2.
Tatua mfumo kwa kubadilisha:$\left\{\begin{array}{l}{x-4 y=-4} \\ {-3 x+4 y=0}\end{array}\right.$
Ikiwa umekosa tatizo hili, kagua Mfano 4.7.
Tatua mfumo kwa kuondoa:$\left\{\begin{array}{l}{3 x-4 y=-9} \\ {5 x+3 y=14}\end{array}\right.$
Ikiwa umekosa tatizo hili, kagua Mfano 4.9.

Tatua Mfumo wa Equations isiyo ya kawaida kwa kutumia Graphing

Tulijifunza jinsi ya kutatua mifumo ya usawa wa mstari na vigezo viwili kwa kuchora, kubadilisha na kuondoa. Tutakuwa kutumia mbinu hizi sawa na sisi kuangalia mifumo nonlinear ya milinganyo na equations mbili na vigezo mbili. Mfumo wa milinganyo isiyo ya kawaida ni mfumo ambapo angalau moja ya equations si linear.

Kwa mfano kila moja ya mifumo ifuatayo ni mfumo wa milinganyo isiyo ya kawaida.

$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right. \left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right. \left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$

Ufafanuzi$\PageIndex{1}$

Mfumo wa milinganyo isiyo ya kawaida ni mfumo ambapo angalau moja ya equations si linear.

Kama ilivyo na mifumo ya equations linear, ufumbuzi wa mfumo usio na mstari ni jozi iliyoamriwa ambayo inafanya equations zote mbili kweli. Katika mfumo usio na mstari, kunaweza kuwa na suluhisho zaidi ya moja. Tutaona hii kama sisi kutatua mfumo wa equations nonlinear kwa graphing.

Tulipotatua mifumo ya equations linear, ufumbuzi wa mfumo ulikuwa hatua ya makutano ya mistari miwili. Kwa mifumo ya equations isiyo ya kawaida, grafu inaweza kuwa miduara, parabolas au hyperbolas na kunaweza kuwa na pointi kadhaa za makutano, na hivyo ufumbuzi kadhaa. Mara baada ya kutambua grafu, taswira njia tofauti ambazo grafu zinaweza kuingiliana na hivyo ni ufumbuzi wangapi kunaweza kuwa.

Ili kutatua mifumo ya equations isiyo ya kawaida kwa graphing, tunatumia kimsingi hatua sawa na mifumo ya equations linear iliyopita kidogo kwa equations nonlinear. Hatua zimeorodheshwa hapa chini kwa kumbukumbu.

Tatua Mfumo wa Ulinganisho usio na Nonlinear kwa Graphing.

Tambua grafu ya kila equation. Chora chaguo iwezekanavyo kwa makutano.
Grafu equation ya kwanza.
Grafu equation ya pili kwenye mfumo huo wa kuratibu mstatili.
Kuamua kama grafu intersect.
Tambua pointi za makutano.
Angalia kwamba kila jozi iliyoamriwa ni suluhisho la milinganyo yote ya awali.

Mfano$\PageIndex{1}$

Tatua mfumo kwa kuchora:$\left\{\begin{array}{l}{x-y=-2} \\ {y=x^{2}}\end{array}\right.$

Suluhisho:

Jedwali 11.5.1
Tambua kila grafu.	$\left\{\begin{array}{ll}{x-y=-2} & {\text { line }} \\ {y=x^{2}} & {\text { parabola }}\end{array}\right.$
Mchoro chaguo iwezekanavyo kwa makutano ya parabola na mstari.	$.$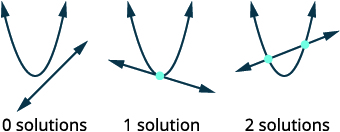
Grafu mstari,$x-y=-2$. Fomu ya kupinga mteremko$y=x+2$. Grafu parabola,$y=x^{2}$.	$.$
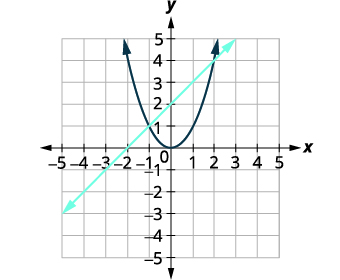Tambua pointi za makutano.	Vipengele vya makutano vinaonekana kuwa$(2,3)$ na$(-1,1)$.
Angalia ili kuhakikisha kila suluhisho hufanya equations zote mbili kweli. $(2,4)$ $\begin{array} {r l } {x-y=-2}\quad\quad {y=x^{2}} \\ {2-4\stackrel{?}{=}-2}\quad\quad {4\stackrel{?}{=}2^{2}} \\ {-2 = -2}\quad\quad\:{4 = 4} \end{array}$ $(-1,1)$ $\begin{array} {l l } {x-y=-2}\quad\quad {y=x^{2}} \\ {-1-1\stackrel{?}{=}-2}\:\quad {1\stackrel{?}{=}(-1)^{2}} \\ {-2 = -2}\quad\quad\quad{1 = 1} \end{array}$
	Ufumbuzi ni$(2,4)$ na$(-1,1)$.

Zoezi$\PageIndex{1}$

Tatua mfumo kwa kuchora:$\left\{\begin{array}{l}{x+y=4} \\ {y=x^{2}+2}\end{array}\right.$.

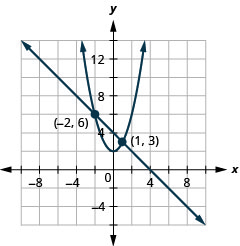
Jibu: $Grafu hii inaonyesha equations ya mfumo, x plus y ni sawa na 4 na y ni sawa x squared pamoja na 2, na x y-kuratibu ndege. Mstari una mteremko wa hasi 1 na y-intercept saa 4. Vertex ya parabola ni (0, 2) na inafungua juu. Mstari na parabola huingiliana kwenye pointi (hasi 2, 6) na (1, 3), ambazo zimeandikwa.$
Kielelezo 11.5.3

Zoezi$\PageIndex{2}$

Tatua mfumo kwa kuchora:$\left\{\begin{array}{l}{x-y=-1} \\ {y=-x^{2}+3}\end{array}\right.$

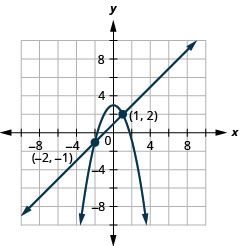
Jibu: $Grafu hii inaonyesha equations ya mfumo, x minus y ni sawa na hasi 1 na y ni sawa na hasi x squared pamoja na tatu, na x y-kuratibu ndege. Mstari una mteremko wa 1 na y-intercept saa 1. Vertex ya parabola ni (0, hasi 3) na inafungua juu. Mstari na parabola huingiliana kwenye pointi (hasi 2, hasi 1) na (1, 2), ambazo zimeandikwa.$
Kielelezo 11.5.4

Ili kutambua grafu ya kila equation, kukumbuka sifa za$x^{2}$ na$y^{2}$ masharti ya kila conic.

Mfano$\PageIndex{2}$

Tatua mfumo kwa kuchora:$\left\{\begin{array}{l}{y=-1} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$.

Suluhisho:

Jedwali 11.5.2
Tambua kila grafu.	$\left\{\begin{array}{ll}{y=-1} & {\text { line }} \\ {(x-2)^{2}+(y+3)^{2}=4} & {\text { circle }}\end{array}\right.$
Chora chaguo iwezekanavyo kwa makutano ya mduara na mstari.	$.$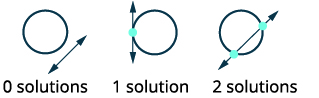
Grafu mduara,$(x-2)^{2}+(y+3)^{2}=4$ Kituo:$(2,-3)$ radius:$2$ Grafu mstari,$y=-1$. Ni mstari usio na usawa.	$.$
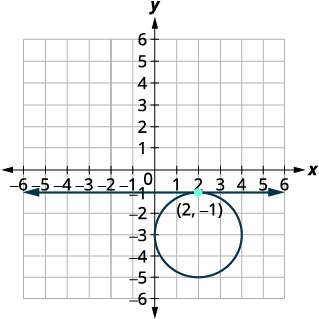Tambua pointi za makutano.	Hatua ya makutano inaonekana kuwa$(2,-1)$.
Angalia ili uhakikishe ufumbuzi hufanya equations zote mbili kweli. $(2,-1)$ $\begin{array} {r r} {(x-2)^{2}+(y+3)^{2}=4} \quad\quad {y=-1} \\ {(2-2)^{2}+(-1+3)^{2}\stackrel{?}{=}4}\quad{-1=-1} \\ {(0)^{2}+(2)^{2}\stackrel{?}{=}4}\quad\quad\quad\quad\quad \\ {4=4}\quad\quad\quad\quad\quad \end{array}$
	Suluhisho ni$(2,-1)$

Zoezi$\PageIndex{3}$

Tatua mfumo kwa kuchora:$\left\{\begin{array}{l}{x=-6} \\ {(x+3)^{2}+(y-1)^{2}=9}\end{array}\right.$

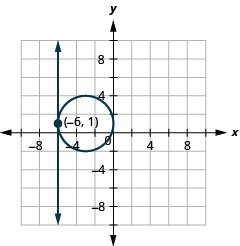
Jibu: $Grafu hii inaonyesha equations ya mfumo, x ni sawa na hasi 6 na kiasi x pamoja na 3 squared pamoja na wingi y minus 1 squared ni sawa na 9, ambayo ni mduara, kwenye ndege ya kuratibu x y. Mstari ni mstari wa wima. Katikati ya mduara ni (hasi 3, 1) na ina radius ya vitengo 3. Hatua ya makutano kati ya mstari na mduara ni (hasi 6, 1).$
Kielelezo 11.5.7

Zoezi$\PageIndex{4}$

Tatua mfumo kwa kuchora:$\left\{\begin{array}{l}{y=4} \\ {(x-2)^{2}+(y+3)^{2}=4}\end{array}\right.$

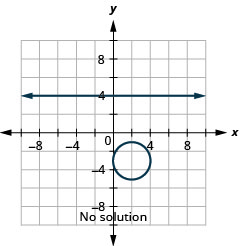
Jibu: $Grafu hii inaonyesha equations ya mfumo, y ni sawa na hasi 4 na kiasi x minus 2 squared pamoja na wingi y pamoja na 3 squared ni sawa na 4, ambayo ni mduara, kwenye ndege ya kuratibu x y. Mstari ni mstari usio na usawa. Katikati ya mduara ni (2, hasi 3) na ina radius ya vitengo 2. Hakuna hatua ya makutano kati ya mstari na mduara, hivyo mfumo hauna suluhisho.$
Kielelezo 11.5.8

Tatua Mfumo wa Ulinganisho usio wa kawaida Kutumia Kubadilisha

Njia ya kuchora inafanya kazi vizuri wakati pointi za makutano ni integers na rahisi kusoma grafu. Lakini mara nyingi ni vigumu kusoma kuratibu za pointi za makutano. Njia ya kubadilisha ni njia ya algebraic ambayo itafanya kazi vizuri katika hali nyingi. Inafanya kazi vizuri hasa wakati ni rahisi kutatua moja ya equations kwa moja ya vigezo.

Njia ya kubadilisha ni sawa na njia ya kubadilisha ambayo tulitumia kwa mifumo ya equations linear. Hatua zimeorodheshwa hapa chini kwa kumbukumbu.

Tatua Mfumo wa Ulinganisho usio na Nonlinear kwa Kubadilisha

Tambua grafu ya kila equation. Chora chaguo iwezekanavyo kwa makutano.
Kutatua moja ya milinganyo kwa variable ama.
Badilisha usemi kutoka Hatua ya 2 katika equation nyingine.
Tatua equation inayosababisha.
Mbadala kila ufumbuzi katika Hatua ya 4 katika moja ya milinganyo ya awali ili kupata variable nyingine.
Andika kila suluhisho kama jozi iliyoamriwa.
Angalia kwamba kila jozi iliyoamriwa ni suluhisho la milinganyo yote ya awali.

Mfano$\PageIndex{3}$

Tatua mfumo kwa kutumia mbadala:$\left\{\begin{array}{l}{9 x^{2}+y^{2}=9} \\ {y=3 x-3}\end{array}\right.$

Suluhisho:

Jedwali 11.5.3
Tambua kila grafu.	$\left\{\begin{array}{ll}{9 x^{2}+y^{2}=9} & {\text { ellipse }} \\ {y=3 x-3} & {\text { line }}\end{array}\right.$
Mchoro chaguo iwezekanavyo kwa makutano ya ellipse na mstari.	$.$
equation$y=3x-3$ ni kutatuliwa kwa$y$.	$.$
	$.$
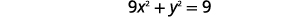Mbadala$3x-3$ kwa ajili ya$y$ katika equation kwanza.	$.$
Kutatua equation kwa$x$.	$.$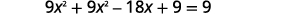
	$.$
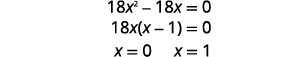Mbadala$x=0$ na$x=1$ katika$y=3x-3$ kupata$y$ -.	$.$
	$.$
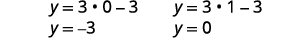	Jozi zilizoamriwa ni$(0,-3), (1,0)$.
Angalia jozi zote mbili zilizoamriwa katika equations zote mbili. $(0,-3)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot0^{2}+(-3)^{2}\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}3\cdot0-3} \\ {0+9\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}0-3} \\ {9=9}&\quad{-3=-3} \end{array}$ $(1,0)$ $\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot 1^{2}+(0)^{2}\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3\cdot 1-3} \\ {9+0\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3-3} \\ {9=9}&\quad{0=0} \end{array}$
	Ufumbuzi ni$(0,-3), (1,0)$.

Zoezi$\PageIndex{5}$

Tatua mfumo kwa kutumia mbadala:$\left\{\begin{array}{l}{x^{2}+9 y^{2}=9} \\ {y=\frac{1}{3} x-3}\end{array}\right.$

Jibu: Hakuna ufumbuzi

Zoezi$\PageIndex{6}$

Tatua mfumo kwa kutumia mbadala:$\left\{\begin{array}{l}{4 x^{2}+y^{2}=4} \\ {y=x+2}\end{array}\right.$

Jibu: $\left(-\frac{4}{5}, \frac{6}{5}\right),(0,2)$

Hadi sasa, kila mfumo wa equations nonlinear imekuwa na ufumbuzi angalau moja. Mfano unaofuata utaonyesha chaguo jingine.

Mfano$\PageIndex{4}$

Tatua mfumo kwa kutumia mbadala:$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=x-2}\end{array}\right.$

Suluhisho:

Jedwali 11.5.4
Tambua kila grafu.	$\left\{\begin{array}{ll}{x^{2}-y=0} & {\text { parabola }} \\ {y=x-2} & {\text { line }}\end{array}\right.$
Mchoro chaguo iwezekanavyo kwa makutano ya parabola na mstari.	$.$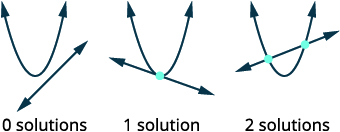
equation$y=x-2$ ni kutatuliwa kwa$y$.	$.$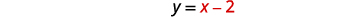
	$.$
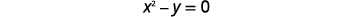Mbadala$x-2$ kwa ajili ya$y$ katika equation kwanza.	$.$
Kutatua equation kwa$x$.	$.$
Hii haina sababu kwa urahisi, hivyo tunaweza kuangalia ubaguzi.
$\begin{array}{c}{b^{2}-4 a c} \\ {(-1)^{2}-4 \cdot 1 \cdot 2} \\ {-7}\end{array}$	Wabaguzi ni hasi, kwa hiyo hakuna suluhisho halisi. Mfumo hauna suluhisho.

Zoezi$\PageIndex{7}$

Tatua mfumo kwa kutumia mbadala:$\left\{\begin{array}{l}{x^{2}-y=0} \\ {y=2 x-3}\end{array}\right.$

Jibu: Hakuna ufumbuzi

Zoezi$\PageIndex{8}$

Tatua mfumo kwa kutumia mbadala:$\left\{\begin{array}{l}{y^{2}-x=0} \\ {y=3 x-2}\end{array}\right.$

Jibu: $\left(\frac{4}{9},-\frac{2}{3}\right),(1,1)$

Kutatua Mfumo wa Equations Nonlinear Kutumia Kuondoa

Tulipojifunza mifumo ya equations linear, tulitumia njia ya kuondoa kutatua mfumo. Tunaweza pia kutumia kuondoa kutatua mifumo ya equations nonlinear. Ni kazi vizuri wakati equations na vigezo vyote viwili squared. Wakati wa kutumia kuondoa, tunajaribu kufanya coefficients ya kutofautiana moja kuwa kinyume, hivyo wakati sisi kuongeza equations pamoja, kwamba variable ni kuondolewa.

Njia ya kuondoa ni sawa na njia ya kuondoa ambayo tulitumia kwa mifumo ya equations linear. Hatua zimeorodheshwa kwa kumbukumbu.

Tatua Mfumo wa Equations kwa Kuondoa

Tambua grafu ya kila equation. Chora chaguo iwezekanavyo kwa makutano.
Andika equations zote mbili kwa fomu ya kawaida.
Fanya coefficients ya kinyume kimoja cha kutofautiana.
Chagua ni variable gani utaondoa.
Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume.
Ongeza milinganyo inayotokana na Hatua ya 3 ili kuondoa variable moja.
Tatua kwa kutofautiana iliyobaki.
Badilisha kila suluhisho kutoka Hatua ya 5 kwenye moja ya milinganyo ya awali. Kisha kutatua kwa variable nyingine.
Andika kila suluhisho kama jozi iliyoamriwa.
Angalia kwamba kila jozi iliyoamriwa ni suluhisho la milinganyo yote ya awali.

Mfano$\PageIndex{5}$

Tatua mfumo kwa kuondoa:$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y=4}\end{array}\right.$

Suluhisho:

Jedwali 11.5.5
Tambua kila grafu.	$.$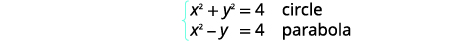
Mchoro chaguo iwezekanavyo kwa makutano ya mduara na parabola.	$.$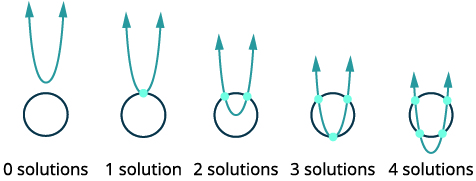
Equations zote mbili ziko katika fomu ya kawaida.	$.$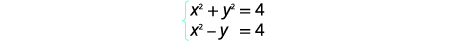
Kupata coefficients kinyume cha$x^{2}$, sisi kuzidisha equation pili na$-1$.	$.$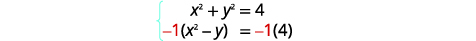
Kurahisisha.	$.$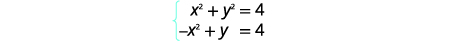
Ongeza equation mbili ili kuondoa$x^{2}$/	$.$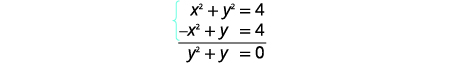
Kutatua kwa$y$.	$.$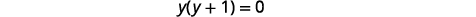
	$.$
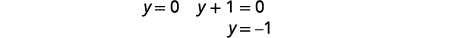Mbadala$y=0$ na$y=-1$ katika moja ya milinganyo ya awali. Kisha kutatua kwa$x$.	$.$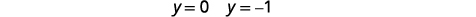
	$.$
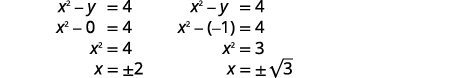Andika kila suluhisho kama jozi iliyoamriwa.	Jozi zilizoamriwa ni$(-2,0)(2,0)$. $(\sqrt{3},-1)(-\sqrt{3},-1)$
Angalia kwamba kila jozi iliyoamriwa ni suluhisho la milinganyo yote ya awali.
Tutaacha hundi kwa kila ufumbuzi wa nne kwako.	Ufumbuzi ni$(-2,0),(2,0),(\sqrt{3},-1)$, na$(-\sqrt{3},-1)$.

Zoezi$\PageIndex{9}$

Tatua mfumo kwa kuondoa:$\left\{\begin{array}{l}{x^{2}+y^{2}=9} \\ {x^{2}-y=9}\end{array}\right.$

Jibu: $(-3,0),(3,0),(-2 \sqrt{2},-1),(2 \sqrt{2},-1)$

Zoezi$\PageIndex{10}$

Tatua mfumo kwa kuondoa:$\left\{\begin{array}{l}{x^{2}+y^{2}=1} \\ {-x+y^{2}=1}\end{array}\right.$

Jibu: $(-1,0),(0,1),(0,-1)$

Pia kuna chaguzi nne wakati tunazingatia mduara na hyperbola.

Mfano$\PageIndex{6}$

Tatua mfumo kwa kuondoa:$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$

Suluhisho:

Jedwali 11.5.6
Tambua kila grafu.	$\left\{\begin{array}{ll}{x^{2}+y^{2}=7} & {\text { circle }} \\ {x^{2}-y^{2}=1} & {\text { hyperbola }}\end{array}\right.$
Mchoro chaguo iwezekanavyo kwa makutano ya mduara na hyperbola.	$.$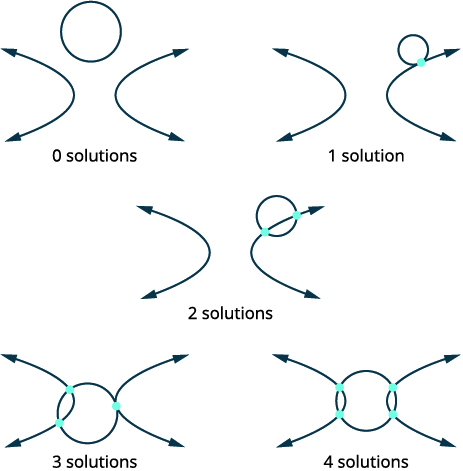
Equations zote mbili ziko katika fomu ya kawaida.	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$
Coefficients ya$y^{2}$ ni kinyume, hivyo tutaongeza equations.	$\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.$ $2 x^{2}=8$
Kurahisisha.	$x^{2}=4$ $x=\pm 2$ $x=2 \quad x=-2$
Badilisha$x=2$ na$x=-2$ katika moja ya milinganyo ya awali. Kisha kutatua kwa$y$.	$\begin{array}{rl}{x^{2}+y^{2} = 7} &\quad { x^{2}+y^{2}=7} \\ {2^{2}+y^{2}=7} & \quad{(-2)^{2}+y^{2}=7} \\ {4+y^{2}=7} &\quad {4+y^{2}=7} \\ {y^{2}=3} &\quad {y^{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{array}$
Andika kila suluhisho kama jozi iliyoamriwa.	Jozi zilizoamriwa ni$(-2, \sqrt{3}),(-2,-\sqrt{3})$,$(2, \sqrt{3}),$ na$(2,-\sqrt{3})$.
Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.
Tutaacha hundi kwa kila ufumbuzi wa nne kwako.	Ufumbuzi ni$(-2, \sqrt{3}),(-2,-\sqrt{3}),(2, \sqrt{3})$, na$(2,-\sqrt{3})$.

Zoezi$\PageIndex{11}$

Tatua mfumo kwa kuondoa:$\left\{\begin{array}{l}{x^{2}+y^{2}=25} \\ {y^{2}-x^{2}=7}\end{array}\right.$

Jibu: $(-3,-4),(-3,4),(3,-4),(3,4)$

Zoezi$\PageIndex{12}$

Tatua mfumo kwa kuondoa:$\left\{\begin{array}{l}{x^{2}+y^{2}=4} \\ {x^{2}-y^{2}=4}\end{array}\right.$

Jibu: $(-2,0),(2,0)$

Tumia Mfumo wa Equations isiyo ya kawaida ili kutatua Maombi

Mifumo ya equations isiyo ya kawaida inaweza kutumika kutengeneza na kutatua programu nyingi. Tutaangalia hali ya kila siku ya kijiometri kama mfano wetu.

Mfano$\PageIndex{7}$

Tofauti ya mraba wa namba mbili ni$15$. Jumla ya idadi ni$5$. Kupata idadi.

Suluhisho:

Jedwali 11.5.7
Tambua kile tunachotafuta.	Nambari mbili tofauti.
Eleza vigezo.	$x$=namba ya kwanza $y$=namba ya pili
Tafsiri habari katika mfumo wa equations.
Sentensi ya kwanza.	Tofauti ya mraba wa namba mbili ni$15$.
	$.$
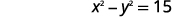Sentensi ya pili.	Jumla ya idadi ni$5$.
	$.$
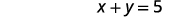Tatua mfumo kwa kubadilisha.	$.$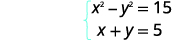
Kutatua equation pili kwa$x$.	$.$
Mbadala$x$ katika equation kwanza.	$.$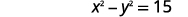
	$.$
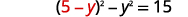Panua na kurahisisha.	$.$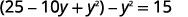
	$.$
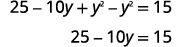Kutatua kwa$y$.	$.$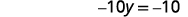
	$.$
Mbadala nyuma katika equation pili.	$.$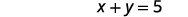
	$.$
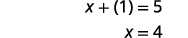	Idadi ni$1$ na$4$.

Zoezi$\PageIndex{13}$

Tofauti ya mraba wa namba mbili ni$−20$. Jumla ya idadi ni$10$. Kupata idadi.

Jibu: $4$na$6$

Zoezi$\PageIndex{14}$

Tofauti ya mraba wa namba mbili ni$35$. Jumla ya idadi ni$−1$. Kupata idadi.

Jibu: $-18$na$17$

Mfano$\PageIndex{8}$

Myra alinunua TV ndogo$25$” kwa ajili ya jikoni yake. Ukubwa wa TV hupimwa kwenye diagonal ya skrini. Skrini pia ina eneo la inchi za$300$ mraba. Urefu na upana wa skrini ya TV ni nini?

Suluhisho:

Jedwali 11.5.8
Tambua kile tunachotafuta.	Urefu na upana wa mstatili.
Eleza vigezo.	Hebu$x$ = upana wa mstatili $y$=urefu wa mstatili
Chora mchoro ili kusaidia kutazama hali hiyo.	$.$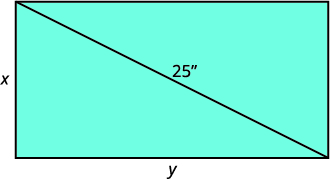
	Eneo ni inchi$300$ za mraba.
Tafsiri habari katika mfumo wa equations.	Ulalo wa pembetatu sahihi ni$25$ inchi.
	$.$
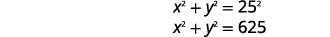	Eneo la mstatili ni inchi$300$ za mraba.
	$.$
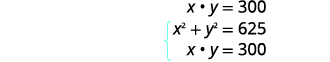Tatua mfumo kwa kutumia ubadilishaji.	$.$
Kutatua equation pili kwa$x$.	$.$
Mbadala$x$ katika equation kwanza.	$.$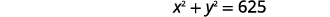
	$.$
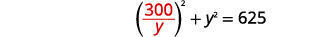Kurahisisha.	$.$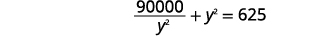
$y^{2}$Kuzidisha kwa kufuta sehemu ndogo.	$.$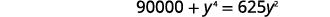
Weka katika fomu ya kawaida.	$.$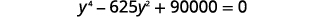
Kutatua kwa factoring.	$.$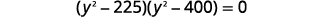
	$.$
	$.$
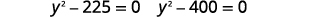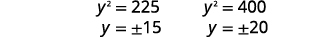Kwa kuwa$y$ ni upande wa mstatili, tunaondoa maadili hasi.	$.$
Mbadala nyuma katika equation pili.	$.$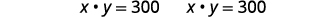
	$.$
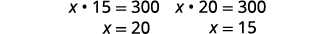	Ikiwa urefu ni$15$ inchi, upana ni$20$ inchi.
	Ikiwa urefu ni$20$ inchi, upana ni$15$ inchi.

Zoezi$\PageIndex{15}$

Edgar alinunua TV ndogo$20$” kwa karakana yake. Ukubwa wa TV hupimwa kwenye diagonal ya skrini. Skrini pia ina eneo la inchi za$192$ mraba. Urefu na upana wa skrini ya TV ni nini?

Jibu: Ikiwa urefu ni$12$ inchi, upana ni$16$ inchi. Ikiwa urefu ni$16$ inchi, upana ni$12$ inchi.

Zoezi$\PageIndex{16}$

Familia ya Harper ilinunua microwave ndogo kwa chumba cha familia zao. Ulalo wa mlango hupima$15$ inchi. Mlango pia una eneo la inchi za$108$ mraba. Urefu na upana wa mlango wa microwave ni nini?

Jibu: Ikiwa urefu ni$12$ inchi, upana ni$9$ inchi. Ikiwa urefu ni$9$ inchi, upana ni$12$ inchi.

Kupata rasilimali hizi online kwa maelekezo ya ziada na mazoezi na kutatua equations nonlinear.

Mifumo isiyo ya kawaida ya Ulinganisho
Tatua Mfumo wa Ulinganisho usio na Nonlinear
Tatua Mfumo wa Ulinganisho usio na Nonlinear kwa Kuondoa
Mfumo wa Ulinganisho usio wa kawaida - Maombi ya Eneo na Mzunguko

Dhana muhimu

Jinsi ya kutatua mfumo wa equations nonlinear kwa graphing.
1. Tambua grafu ya kila equation. Chora chaguo iwezekanavyo kwa makutano.
2. Grafu equation ya kwanza.
3. Grafu equation ya pili kwenye mfumo huo wa kuratibu mstatili.
4. Kuamua kama grafu intersect.
5. Tambua pointi za makutano.
6. Angalia kwamba kila jozi iliyoamriwa ni suluhisho la milinganyo yote ya awali.
Jinsi ya kutatua mfumo wa equations nonlinear na badala.
1. Tambua grafu ya kila equation. Chora chaguo iwezekanavyo kwa makutano.
2. Kutatua moja ya milinganyo kwa variable ama.
3. Badilisha usemi kutoka Hatua ya 2 katika equation nyingine.
4. Tatua equation inayosababisha.
5. Mbadala kila ufumbuzi katika Hatua ya 4 katika moja ya milinganyo ya awali ili kupata variable nyingine.
6. Andika kila suluhisho kama jozi iliyoamriwa.
7. Angalia kwamba kila jozi iliyoamriwa ni suluhisho la milinganyo yote ya awali.
Jinsi ya kutatua mfumo wa equations kwa kuondoa.
1. Tambua grafu ya kila equation. Chora chaguo iwezekanavyo kwa makutano.
2. Andika equations zote mbili kwa fomu ya kawaida.
3. Fanya coefficients ya kinyume kimoja cha kutofautiana.
  Chagua ni variable gani utaondoa.
  Kuzidisha equations moja au zote mbili ili coefficients ya kutofautiana kuwa ni kinyume.
4. Ongeza milinganyo inayotokana na Hatua ya 3 ili kuondoa variable moja.
5. Tatua kwa kutofautiana iliyobaki.
6. Badilisha kila suluhisho kutoka Hatua ya 5 kwenye moja ya milinganyo ya awali. Kisha kutatua kwa variable nyingine.
7. Andika kila suluhisho kama jozi iliyoamriwa.
8. Angalia kwamba kila jozi iliyoamriwa ni suluhisho la milinganyo yote ya awali.

Tambua kila grafu.	\(\left\{\begin{array}{ll}{x^{2}+y^{2}=7} & {\text { circle }} \\ {x^{2}-y^{2}=1} & {\text { hyperbola }}\end{array}\right.\)
Mchoro chaguo iwezekanavyo kwa makutano ya mduara na hyperbola.	$.$
Equations zote mbili ziko katika fomu ya kawaida.	\(\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.\)
Coefficients ya\(y^{2}\) ni kinyume, hivyo tutaongeza equations.	\(\left\{\begin{array}{l}{x^{2}+y^{2}=7} \\ {x^{2}-y^{2}=1}\end{array}\right.\) \(2 x^{2}=8\)
Kurahisisha.	\(x^{2}=4\) \(x=\pm 2\) \(x=2 \quad x=-2\)
Badilisha\(x=2\) na\(x=-2\) katika moja ya milinganyo ya awali. Kisha kutatua kwa\(y\).	\(\begin{array}{rl}{x^{2}+y^{2} = 7} &\quad { x^{2}+y^{2}=7} \\ {2^{2}+y^{2}=7} & \quad{(-2)^{2}+y^{2}=7} \\ {4+y^{2}=7} &\quad {4+y^{2}=7} \\ {y^{2}=3} &\quad {y^{2}=3} \\ {y=\pm \sqrt{3}} &\quad {y=\pm \sqrt{3}}\end{array}\)
Andika kila suluhisho kama jozi iliyoamriwa.	Jozi zilizoamriwa ni\((-2, \sqrt{3}),(-2,-\sqrt{3})\),\((2, \sqrt{3}),\) na\((2,-\sqrt{3})\).
Angalia kwamba jozi iliyoamriwa ni suluhisho la equations zote za awali.
Tutaacha hundi kwa kila ufumbuzi wa nne kwako.	Ufumbuzi ni\((-2, \sqrt{3}),(-2,-\sqrt{3}),(2, \sqrt{3})\), na\((2,-\sqrt{3})\).

Ufafanuzi\(\PageIndex{1}\)

Mfano\(\PageIndex{1}\)

Zoezi\(\PageIndex{1}\)

Zoezi\(\PageIndex{2}\)

Mfano\(\PageIndex{2}\)

Zoezi\(\PageIndex{3}\)

Zoezi\(\PageIndex{4}\)

Mfano\(\PageIndex{3}\)

Zoezi\(\PageIndex{5}\)

Zoezi\(\PageIndex{6}\)

Mfano\(\PageIndex{4}\)

Zoezi\(\PageIndex{7}\)

Zoezi\(\PageIndex{8}\)

Mfano\(\PageIndex{5}\)

Zoezi\(\PageIndex{9}\)

Zoezi\(\PageIndex{10}\)

Mfano\(\PageIndex{6}\)

Zoezi\(\PageIndex{11}\)

Zoezi\(\PageIndex{12}\)

Mfano\(\PageIndex{7}\)

Zoezi\(\PageIndex{13}\)

Zoezi\(\PageIndex{14}\)

Mfano\(\PageIndex{8}\)

Zoezi\(\PageIndex{15}\)

Zoezi\(\PageIndex{16}\)

Tambua kila grafu.	\(\left\{\begin{array}{ll}{x-y=-2} & {\text { line }} \\ {y=x^{2}} & {\text { parabola }}\end{array}\right.\)
Mchoro chaguo iwezekanavyo kwa makutano ya parabola na mstari.	$.$
Grafu mstari,\(x-y=-2\). Fomu ya kupinga mteremko\(y=x+2\). Grafu parabola,\(y=x^{2}\).	$.$
Tambua pointi za makutano.	Vipengele vya makutano vinaonekana kuwa\((2,3)\) na\((-1,1)\).
Angalia ili kuhakikisha kila suluhisho hufanya equations zote mbili kweli. \((2,4)\) \(\begin{array} {r l } {x-y=-2}\quad\quad {y=x^{2}} \\ {2-4\stackrel{?}{=}-2}\quad\quad {4\stackrel{?}{=}2^{2}} \\ {-2 = -2}\quad\quad\:{4 = 4} \end{array}\) \((-1,1)\) \(\begin{array} {l l } {x-y=-2}\quad\quad {y=x^{2}} \\ {-1-1\stackrel{?}{=}-2}\:\quad {1\stackrel{?}{=}(-1)^{2}} \\ {-2 = -2}\quad\quad\quad{1 = 1} \end{array}\)
	Ufumbuzi ni\((2,4)\) na\((-1,1)\).

Tambua kila grafu.	\(\left\{\begin{array}{ll}{y=-1} & {\text { line }} \\ {(x-2)^{2}+(y+3)^{2}=4} & {\text { circle }}\end{array}\right.\)
Chora chaguo iwezekanavyo kwa makutano ya mduara na mstari.	$.$
Grafu mduara,\((x-2)^{2}+(y+3)^{2}=4\) Kituo:\((2,-3)\) radius:\(2\) Grafu mstari,\(y=-1\). Ni mstari usio na usawa.	$.$
Tambua pointi za makutano.	Hatua ya makutano inaonekana kuwa\((2,-1)\).
Angalia ili uhakikishe ufumbuzi hufanya equations zote mbili kweli. \((2,-1)\) \(\begin{array} {r r} {(x-2)^{2}+(y+3)^{2}=4} \quad\quad {y=-1} \\ {(2-2)^{2}+(-1+3)^{2}\stackrel{?}{=}4}\quad{-1=-1} \\ {(0)^{2}+(2)^{2}\stackrel{?}{=}4}\quad\quad\quad\quad\quad \\ {4=4}\quad\quad\quad\quad\quad \end{array}\)
	Suluhisho ni\((2,-1)\)

Tambua kila grafu.	\(\left\{\begin{array}{ll}{9 x^{2}+y^{2}=9} & {\text { ellipse }} \\ {y=3 x-3} & {\text { line }}\end{array}\right.\)
Mchoro chaguo iwezekanavyo kwa makutano ya ellipse na mstari.	$.$
equation\(y=3x-3\) ni kutatuliwa kwa\(y\).	$.$
	$.$
Mbadala\(3x-3\) kwa ajili ya\(y\) katika equation kwanza.	$.$
Kutatua equation kwa\(x\).	$.$
	$.$
Mbadala\(x=0\) na\(x=1\) katika\(y=3x-3\) kupata\(y\) -.	$.$
	$.$
	Jozi zilizoamriwa ni\((0,-3), (1,0)\).
Angalia jozi zote mbili zilizoamriwa katika equations zote mbili. \((0,-3)\) \(\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot0^{2}+(-3)^{2}\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}3\cdot0-3} \\ {0+9\stackrel{?}{=}9}&\quad{-3\stackrel{?}{=}0-3} \\ {9=9}&\quad{-3=-3} \end{array}\) \((1,0)\) \(\begin{array} {r l}{9 x^{2}+y^{2}=9} &\quad { y=3 x-3} \\ {9\cdot 1^{2}+(0)^{2}\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3\cdot 1-3} \\ {9+0\stackrel{?}{=}9}&\quad{0\stackrel{?}{=}3-3} \\ {9=9}&\quad{0=0} \end{array}\)
	Ufumbuzi ni\((0,-3), (1,0)\).

Tambua kila grafu.	\(\left\{\begin{array}{ll}{x^{2}-y=0} & {\text { parabola }} \\ {y=x-2} & {\text { line }}\end{array}\right.\)
Mchoro chaguo iwezekanavyo kwa makutano ya parabola na mstari.	$.$
equation\(y=x-2\) ni kutatuliwa kwa\(y\).	$.$
	$.$
Mbadala\(x-2\) kwa ajili ya\(y\) katika equation kwanza.	$.$
Kutatua equation kwa\(x\).	$.$
Hii haina sababu kwa urahisi, hivyo tunaweza kuangalia ubaguzi.
\(\begin{array}{c}{b^{2}-4 a c} \\ {(-1)^{2}-4 \cdot 1 \cdot 2} \\ {-7}\end{array}\)	Wabaguzi ni hasi, kwa hiyo hakuna suluhisho halisi. Mfumo hauna suluhisho.