9.6: Informações adicionais e exemplos completos de testes de hipóteses

Last updated
Save as PDF

Page ID: 190304

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Em um problema de teste de hipótese, você pode ver palavras como “o nível de significância é 1%”. O "1%" é o preconcebido ou predefinido$\alpha$.
O estatístico que configura o teste de hipótese seleciona o valor de α a ser usado antes de coletar os dados da amostra.
Se nenhum nível de significância for dado, um padrão comum a ser usado é$\alpha = 0.05$.
Quando você calcula o$p$ valor -e desenha a figura, o$p$ valor -é a área na cauda esquerda, na cauda direita ou dividida uniformemente entre as duas pontas. Por esse motivo, chamamos o teste de hipótese de esquerdo, direito ou bicaudal.
A hipótese alternativa,$H_{a}$, informa se o teste é esquerdo, direito ou bicaudal. É a chave para realizar o teste apropriado.
$H_{a}$nunca tem um símbolo que contenha um sinal de igual.
Pensando no significado do$p$ valor -: um analista de dados (e qualquer outra pessoa) deve ter mais confiança de que tomou a decisão correta de rejeitar a hipótese nula com um$p$ valor -menor (por exemplo, 0,001 em vez de 0,04), mesmo usando o nível 0,05 para alfa. Da mesma forma, para um grande valor de p, como 0,4, em oposição a um$p$ valor -de 0,056 ($\alpha = 0.05$é menor que qualquer um dos números), um analista de dados deve ter mais confiança de que tomou a decisão correta ao não rejeitar a hipótese nula. Isso faz com que o analista de dados use o julgamento em vez de aplicar regras sem pensar.

Os exemplos a seguir ilustram um teste de esquerda, direita e bicaudal.

Exemplo$\PageIndex{1}$

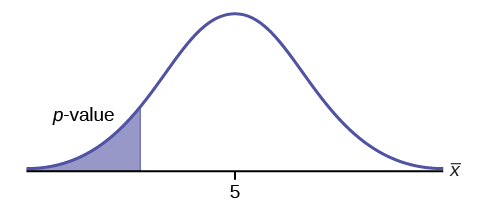
$H_{0}: \mu = 5, H_{a}: \mu < 5$

Teste de uma única média populacional. $H_{a}$diz que o teste é de cauda esquerda. A imagem do$p$ valor -é a seguinte:

Curva de distribuição normal de uma única média populacional com um valor de 5 no eixo x e o valor p aponta para a área na cauda esquerda da curva. — Figura$\PageIndex{1}$

Exercício$\PageIndex{1}$

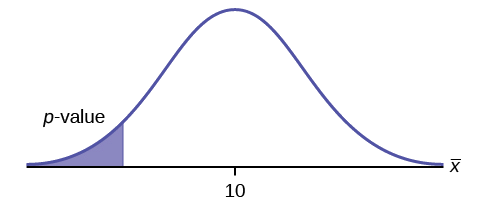
$H_{0}: \mu = 10, H_{a}: \mu < 10$

Suponha que o$p$ valor -seja 0,0935. Que tipo de teste é esse? Desenhe a imagem do$p$ valor -.

Resposta

teste de cauda esquerda

Exemplo$\PageIndex{2}$

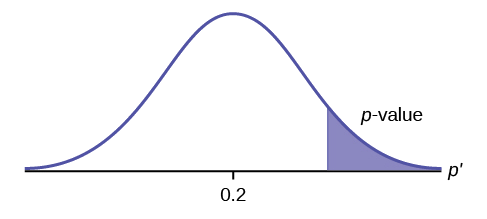
$H_{0}: \mu \leq 0.2, H_{a}: \mu > 0.2$

Este é um teste de uma única proporção populacional. $H_{a}$indica que o teste é de cauda direita. A imagem do valor p é a seguinte:

Curva de distribuição normal de uma única proporção da população com o valor de 0,2 no eixo x. O valor p aponta para a área na extremidade direita da curva. — Figura$\PageIndex{3}$

Exercício$\PageIndex{2}$

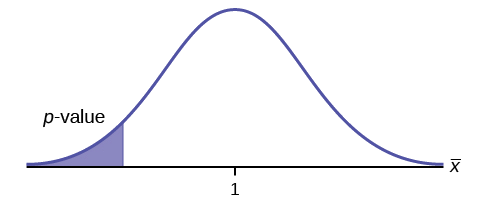
$H_{0}: \mu \leq 1, H_{a}: \mu > 1$

Suponha que o$p$ valor -seja 0,1243. Que tipo de teste é esse? Desenhe a imagem do$p$ valor -.

Resposta

teste com cauda direita

Exemplo$\PageIndex{3}$

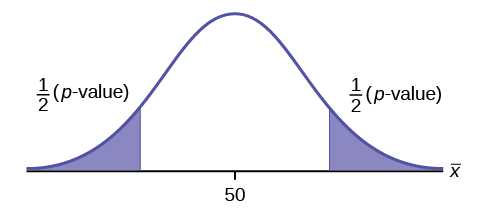
$H_{0}: \mu = 50, H_{a}: \mu \neq 50$

Este é um teste de uma única média populacional. $H_{a}$diz que o teste é bicaudal. A imagem do$p$ valor -é a seguinte.

Curva de distribuição normal de uma única média populacional com um valor de 50 no eixo x. As fórmulas do valor p, 1/2 (valor p), para um teste bicaudal são mostradas para as áreas nas extremidades esquerda e direita da curva. — Figura$\PageIndex{5}$

Exercício$\PageIndex{3}$

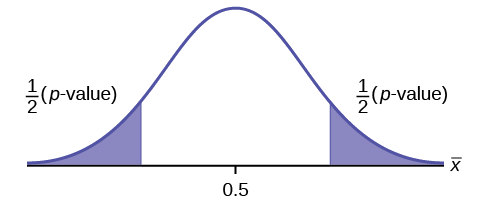
$H_{0}: \mu = 0.5, H_{a}: \mu \neq 0.5$

Suponha que o valor p seja 0,2564. Que tipo de teste é esse? Desenhe a imagem do$p$ valor -.

Resposta

teste bicaudal

Exemplos completos de testes de hipóteses

Exemplo$\PageIndex{4}$

Jeffrey, com oito anos de idade, estabeleceu um tempo médio de 16,43 segundos para nadar no estilo livre de 25 jardas, com um desvio padrão de 0,8 segundos. Seu pai, Frank, achava que Jeffrey poderia nadar no estilo livre de 25 jardas mais rápido usando óculos de proteção. Frank comprou um novo par de óculos caros para Jeffrey e cronometrou Jeffrey para 15 nadadas de 25 jardas em estilo livre. Para os 15 nados, o tempo médio de Jeffrey foi de 16 segundos. Frank achou que os óculos ajudaram Jeffrey a nadar mais rápido do que os 16,43 segundos. Faça um teste de hipótese usando uma predefinição α = 0,05. Suponha que os tempos de natação para o estilo livre de 25 jardas sejam normais.

Resposta

Configure o teste de hipótese:

Como o problema é sobre uma média, este é um teste de uma única média populacional.

$H_{0}: \mu = 16.43, H_{a}: \mu < 16.43$

Para Jeffrey nadar mais rápido, seu tempo será inferior a 16,43 segundos. O "$<$" diz que isso é de cauda esquerda.

Determine a distribuição necessária:

Variável aleatória:$\bar{X} =$ o tempo médio para nadar no estilo livre de 25 jardas.

Distribuição para o teste:$\bar{X}$ é normal (o desvio padrão da população é conhecido:$\sigma = 0.8$)

$\bar{X} - N \left(\mu, \frac{\sigma_{x}}{\sqrt{n}}\right)$Portanto,$\bar{X} - N\left(16.43, \frac{0.8}{\sqrt{15}}\right)$

$\mu = 16.43$vem$H_{0}$ e não dos dados. $\sigma = 0.8$,$n = 15$ e.

Calcule o$p-\text{value}$ usando a distribuição normal para uma média:

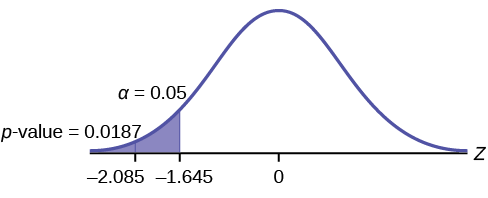
$p\text{-value} = P(\bar{x} < 16) = 0.0187$onde a média da amostra no problema é dada como 16.

$p\text{-value} = 0.0187$(Isso é chamado de nível real de significância.) $p-\text{value}$A área à esquerda da média da amostra é dada como 16.

Gráfico:

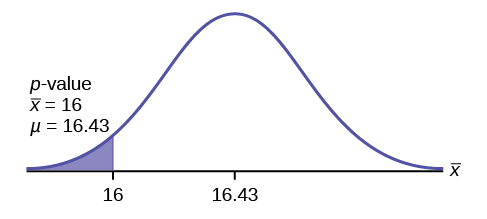
Curva de distribuição normal para o tempo médio de natação no estilo livre de 25 jardas com valores 16, como média da amostra, e 16,43 no eixo x. Uma linha vertical ascendente se estende de 16 no eixo x até a curva. Uma seta aponta para a cauda esquerda da curva. — Figura$\PageIndex{7}$

$\mu = 16.43$vem de$H_{0}$. Nossa suposição é$\mu = 16.43$.

Interpretação do$p-\text{value}$: Se$H_{0}$ for verdade, há uma probabilidade de 0,0187 (1,87%) de que o tempo médio de Jeffrey para nadar no estilo livre de 25 jardas seja de 16 segundos ou menos. Como a chance de 1,87% é pequena, é improvável que o tempo médio de 16 segundos ou menos tenha acontecido aleatoriamente. É um evento raro.

Compare$\alpha$ e o$p-\text{value}$:

$\alpha = 0.05 p\text{-value} = 0.0187 \alpha > p\text{-value}$

Tome uma decisão: desde então$\alpha > p\text{-value}$, rejeite$H_{0}$.

Isso significa que você rejeita$\mu = 16.43$. Em outras palavras, você não acha que Jeffrey nada no estilo livre de 25 jardas em 16,43 segundos, mas mais rápido com os novos óculos.

Conclusão: No nível de significância de 5%, concluímos que Jeffrey nada mais rápido usando os novos óculos. Os dados da amostra mostram que há evidências suficientes de que o tempo médio de Jeffrey para nadar no estilo livre de 25 jardas é inferior a 16,43 segundos.

O valor p pode ser facilmente calculado.

Pressione STAT e vá até TESTS. Pressione 1:Z-Test. Seta até Stats e pressione ENTER. Seta para baixo e insira 16,43 para$\mu_{0}$ (hipótese nula), .8 para σ, 16 para a média da amostra e 15 para n. Seta para baixo até$\mu$: (hipótese alternativa) e seta para$< \mu_{0}$. Pressione ENTER. Seta para baixo até Calcular e pressione ENTER. A calculadora não apenas calcula o valor p ($p = 0.0187$), mas também calcula a estatística de teste (pontuação z) para a média da amostra. $\mu < 16.43$é a hipótese alternativa. Faça esse conjunto de instruções novamente, exceto a seta para desenhar (em vez de calcular). Pressione ENTER. Um gráfico sombreado aparece com$z = -2.08$ (estatística de teste) e$p = 0.0187$ ($p-\text{value}$). Ao usar o Draw, certifique-se de que nenhuma outra equação seja destacada$Y =$ e que os gráficos estejam desativados.

Quando a calculadora faz um$Z$ -Test, a função Z-Test encontra o valor p fazendo um cálculo de probabilidade normal usando o teorema do limite central:

$P(\bar{X} < 16)$2ª norma DISTR cdf ($(−10^{99},16,16.43,\frac{0.8}{\sqrt{15}})$.

Os erros do Tipo I e do Tipo II para esse problema são os seguintes:

O erro Tipo I é concluir que Jeffrey nada no estilo livre de 25 jardas, em média, em menos de 16,43 segundos quando, na verdade, ele realmente nada no estilo livre de 25 jardas, em média, em 16,43 segundos. (Rejeite a hipótese nula quando a hipótese nula for verdadeira.)

O erro do Tipo II é que não há evidências para concluir que Jeffrey nada no estilo livre de 25 jardas, em média, em menos de 16,43 segundos quando, na verdade, ele realmente nada no estilo livre de 25 jardas, em média, em menos de 16,43 segundos. (Não rejeite a hipótese nula quando a hipótese nula for falsa.)

Exercício$\PageIndex{4}$

A distância média de arremesso de uma bola de futebol para um Marco, um quarterback calouro do ensino médio, é de 40 jardas, com um desvio padrão de duas jardas. O técnico da equipe diz a Marco que ajuste sua aderência para obter mais distância. O treinador registra as distâncias de 20 lances. Para os 20 arremessos, a distância média de Marco foi de 45 jardas. O treinador achou que a empunhadura diferente ajudou Marco a arremessar mais de 40 jardas. Faça um teste de hipótese usando uma predefinição$\alpha = 0.05$. Suponha que as distâncias de lançamento das bolas de futebol sejam normais.

Primeiro, determine que tipo de teste é esse, configure o teste de hipótese, encontre o valor p, esboce o gráfico e declare sua conclusão.

Pressione STAT e flecha até TESTS. Pressione 1:$Z$ -Teste. Seta até Stats e pressione ENTER. Seta para baixo e insira 40 para$\mu_{0}$ (hipótese nula), 2 para$\sigma$, 45 para a média da amostra e 20 para$n$. Desça até$\mu$: (hipótese alternativa) e defina-a como$<$$\neq$, ou$>$. Pressione ENTER. Seta para baixo até Calcular e pressione ENTER. A calculadora não apenas calcula o valor p, mas também calcula a estatística de teste (pontuação z) para a média da amostra. Selecione$<$,$\neq$, ou$>$ para a hipótese alternativa. Faça esse conjunto de instruções novamente, exceto a seta para desenhar (em vez de calcular). Pressione ENTER. Um gráfico sombreado aparece com a estatística de teste e$p$ o valor. Ao usar o Draw, certifique-se de que nenhuma outra equação seja destacada$Y =$ e que os gráficos estejam desativados.

Resposta

Como o problema é sobre uma média, este é um teste de uma única média populacional.

$H_{0}: \mu = 40$
$H_{a}: \mu > 40$
$p = 0.0062$

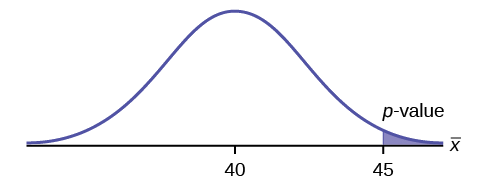
Porque$p < \alpha$ rejeitamos a hipótese nula. Há evidências suficientes para sugerir que a mudança na aderência melhorou a distância de arremesso de Marco.

Nota histórica

A forma tradicional de comparar as duas probabilidades,$\alpha$ e a$p-\text{value}$, é comparar o valor crítico ($z$-score from$\alpha$) com a estatística de teste ($z$-score from data). A estatística de teste calculada para o$p$ valor -é —2,08. (Do Teorema do Limite Central, a fórmula da estatística de teste é$z = \frac{\bar{x}-\mu_{x}}{\left(\frac{\sigma_{x}}{\sqrt{n}}\right)}$. Para esse problema$\bar{x} = 16$,,$\mu_{x} = 16.43$ das hipóteses nulas é$\sigma_{x} = 0.8$,$n = 15$ e.) Você pode encontrar o valor crítico de$\alpha = 0.05$ na tabela normal (consulte 15.Tabelas no Índice). A$z$ pontuação -para uma área à esquerda igual a 0,05 está a meio caminho entre —1,65 e —1,64 (0,05 está a meio caminho entre 0,0505 e 0,0495). O$z$ -score é —1,645. Desde —1.645 > —2.08 (o que demonstra isso$\alpha > p-\text{value}$), rejeite$H_{0}$. Tradicionalmente, a decisão de rejeitar ou não rejeitar era feita dessa maneira. Hoje, comparar as duas probabilidades$\alpha$ e o$p$ valor -é muito comum. Para esse problema$p-\text{value}$, o 0,0187 é consideravelmente menor do que$\alpha = 0.05$. Você pode ter certeza de sua decisão de rejeitar. O gráfico mostra$\alpha$ as$p-\text{value}$ estatísticas do teste e o valor crítico.

Curva de distribuição comparando o α com o valor de p. Valores de -2,15 e -1,645 estão no eixo x. As linhas verticais ascendentes se estendem de ambos os valores até a curva. O valor p é igual a 0,0158 e aponta para a área à esquerda de -2,15. α é igual a 0,05 e aponta para a área entre os valores de -2,15 e -1,645. — Figura$\PageIndex{9}$

Exemplo$\PageIndex{5}$

Um treinador de futebol universitário pensou que seus jogadores poderiam fazer supino com um peso médio de 275 libras. Sabe-se que o desvio padrão é de 55 libras. Três de seus jogadores achavam que o peso médio era maior do que esse valor. Eles pediram a 30 de seus companheiros de equipe a estimativa de levantamento máximo no exercício de supino. Os dados variaram de 205 libras a 385 libras. Os diferentes pesos reais foram (as frequências estão entre parênteses) 205 (3); 215 (3); 225 (1); 241 (2); 252 (2); 265 (2); 275 (2); 313 (2); 316 (5); 338 (2); 341 (1); 345 (2); 368 (2); 385 (2) 1).

Faça um teste de hipótese usando um nível de significância de 2,5% para determinar se a média do supino é superior a 275 libras.

Resposta

Configure o teste de hipótese:

Como o problema é sobre um peso médio, este é um teste de uma única média populacional.

$H_{0}: \mu = 275$
$H_{a}: \mu > 275$

Este é um teste com cauda direita.

Calculando a distribuição necessária:

Variável aleatória:$\bar{X} =$ o peso médio, em libras, levantado pelos jogadores de futebol.

Distribuição para o teste: É normal porque$\sigma$ é conhecido.

$\bar{X} - N\left(275, \frac{55}{\sqrt{30}}\right)$
$\bar{x} = 286.2$libras (a partir dos dados).
$\sigma = 55$libras (Sempre use$\sigma$ se você souber.) Assumimos$\mu = 275$ libras, a menos que nossos dados mostrem o contrário.

Calcule o valor p usando a distribuição normal para uma média e usando a média da amostra como entrada (consulte [link] para usar os dados como entrada):

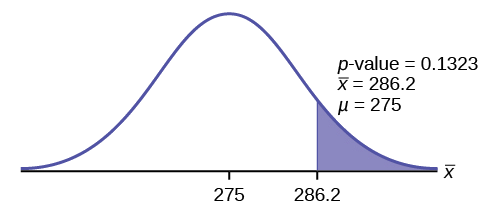
\[p\text{-value} = P(\bar{x} > 286.2) = 0.1323.\nonumber \]

Interpretação do valor p: Se$H_{0}$ for verdade, existe uma probabilidade de 0,1331 (13,23%) de que os jogadores de futebol possam levantar um peso médio de 286,2 libras ou mais. Como uma chance de 13,23% é grande o suficiente, um levantamento de peso médio de 286,2 libras ou mais não é um evento raro.

Curva de distribuição normal do peso médio levantado por jogadores de futebol com valores de 275 e 286,2 no eixo x. Uma linha vertical ascendente se estende de 286,2 até a curva. O valor p aponta para a área à direita de 286,2. — Figura$\PageIndex{10}$

Compare$\alpha$ e o$p-\text{value}$:

$\alpha = 0.025 p-value = 0.1323$

Tome uma decisão: desde então$\alpha < p\text{-value}$, não rejeite$H_{0}$.

Conclusão: No nível de significância de 2,5%, a partir dos dados da amostra, não há evidências suficientes para concluir que o verdadeiro peso médio levantado é superior a 275 libras.

O$p-\text{value}$ pode ser facilmente calculado.

Coloque os dados e as frequências em listas. Pressione STAT e vá até TESTS. Pressione 1:Z-Test. Seta até Data e pressione ENTER. Seta para baixo e digite 275 para$\mu_{0}$$\sigma$, 55 para, o nome da lista em que você colocou os dados e o nome da lista em que você colocou as frequências. Seta para baixo até$\mu$: e seta para$> \mu_{0}$. Pressione ENTER. Seta para baixo até Calcular e pressione ENTER. A calculadora não apenas calcula o$p-\text{value}$ ($p = 0.1331$), um pouco diferente do cálculo anterior - nela usamos a média da amostra (arredondada para uma casa decimal em vez dos dados), mas também calcula a estatística de teste (pontuação z) para a média da amostra, a média da amostra e a desvio padrão da amostra. $\mu > 275$é a hipótese alternativa. Faça esse conjunto de instruções novamente, exceto a seta para desenhar (em vez de calcular). Pressione ENTER. Um gráfico sombreado aparece com$z = 1.112$ (estatística de teste) e$p = 0.1331$ ($p-\text{value})$. Ao usar o Draw, certifique-se de que nenhuma outra equação seja destacada$Y =$ e que os gráficos estejam desativados.

Exemplo$\PageIndex{6}$

Os estudantes de estatística acreditam que a pontuação média no primeiro teste estatístico é 65. Um instrutor de estatística acha que a pontuação média é superior a 65. Ele coleta amostras de dez estudantes de estatística e obtém as pontuações 65 65 70 67 66 63 63 68 72 71. Ele realiza um teste de hipótese usando um nível de significância de 5%. Supõe-se que os dados sejam de uma distribuição normal.

Resposta

Configure o teste de hipótese:

Um nível de significância de 5% significa isso$\alpha = 0.05$. Este é um teste de uma única média populacional.

$H_{0}: \mu = 65 H_{a}: \mu > 65$

Como o instrutor acha que a pontuação média é maior, use um "$>$”. O "$>$" significa que o teste tem cauda direita.

Determine a distribuição necessária:

Variável aleatória: pontuação$\bar{X} =$ média no primeiro teste estatístico.

Distribuição para o teste: Se você ler o problema com atenção, notará que não há desvio padrão da população fornecido. Você só recebe valores$n = 10$ de dados de amostra. Observe também que os dados vêm de uma distribuição normal. Isso significa que a distribuição do teste é de um aluno$t$.

Use$t_{df}$. Portanto, a distribuição para o teste é$t_{9}$ onde$n = 10$$df = 10 - 1 = 9$ e.

Calcule o$p$ valor -usando a$t$ distribuição -de Student:

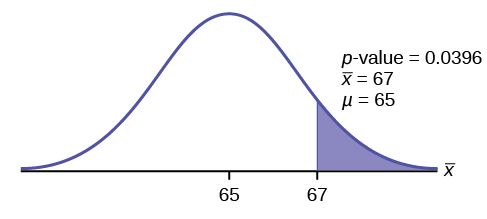
$p\text{-value} = P(\bar{x} > 67) = 0.0396$onde a média da amostra e o desvio padrão da amostra são calculados como 67 e 3,172 a partir dos dados.

Interpretação do valor p: Se a hipótese nula for verdadeira, existe uma probabilidade de 0,0396 (3,96%) de que a média da amostra seja 65 ou mais.

Curva de distribuição normal das pontuações médias nos primeiros testes estatísticos com 65 e 67 valores no eixo x. Uma linha vertical ascendente se estende de 67 até a curva. O valor p aponta para a área à direita de 67. — Figura$\PageIndex{11}$

Compare$\alpha$ e o$p-\text{value}$:

Desde$α = 0.05$$p\text{-value} = 0.0396$ e. $\alpha > p\text{-value}$.

Tome uma decisão: desde então$\alpha > p\text{-value}$, rejeite$H_{0}$.

Isso significa que você rejeita$\mu = 65$. Em outras palavras, você acredita que a pontuação média do teste é superior a 65.

Conclusão: Em um nível de significância de 5%, os dados da amostra mostram evidências suficientes de que a pontuação média (média) do teste é superior a 65, assim como pensa o instrutor de matemática.

O$p\text{-value}$ pode ser facilmente calculado.

Coloque os dados em uma lista. Pressione STAT e vá até TESTS. Pressione 2:T-Test. Seta até Data e pressione ENTER. Seta para baixo e digite 65 para$\mu_{0}$, o nome da lista onde você colocou os dados e 1 para Freq:. Seta para baixo até$\mu$: e seta para$> \mu_{0}$. Pressione ENTER. Seta para baixo até Calcular e pressione ENTER. A calculadora não apenas calcula$p\text{-value}$ (p = 0,0396), mas também calcula a estatística de teste (pontuação t) para a média da amostra, a média da amostra e o desvio padrão da amostra. $\mu > 65$é a hipótese alternativa. Faça esse conjunto de instruções novamente, exceto a seta para desenhar (em vez de calcular). Pressione ENTER. Um gráfico sombreado aparece com$t = 1.9781$ (estatística de teste) e$p = 0.0396$ ($p\text{-value}$). Ao usar o Draw, certifique-se de que nenhuma outra equação seja destacada$Y =$ e que os gráficos estejam desativados.

Exercício$\PageIndex{6}$

Acredita-se que o preço das ações de uma determinada empresa cresça a uma taxa de $5 por semana com um desvio padrão de $1. Um investidor acredita que as ações não crescerão tão rapidamente. As mudanças no preço das ações são registradas por dez semanas e são as seguintes: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Faça um teste de hipótese usando um nível de significância de 5%. Declare as hipóteses nula e alternativa, encontre o valor p, declare sua conclusão e identifique os erros do Tipo I e do Tipo II.

Resposta

$H_{0}: \mu = 5$
$H_{a}: \mu < 5$
$p = 0.0082$

Porque$p < \alpha$ rejeitamos a hipótese nula. Há evidências suficientes para sugerir que o preço das ações da empresa cresce a uma taxa inferior a $5 por semana.

Erro tipo I: Concluir que o preço das ações está crescendo mais lentamente do que $5 por semana, quando, na verdade, o preço das ações está crescendo a $5 por semana (rejeite a hipótese nula quando a hipótese nula for verdadeira).
Erro Tipo II: Concluir que o preço das ações está crescendo a uma taxa de $5 por semana, quando, na verdade, o preço das ações está crescendo mais lentamente do que $5 por semana (não rejeite a hipótese nula quando a hipótese nula for falsa).

Exemplo$\PageIndex{7}$

Joon acredita que 50% das noivas pela primeira vez nos Estados Unidos são mais jovens do que seus noivos. Ela realiza um teste de hipótese para determinar se a porcentagem é igual ou diferente de 50%. Joon mostra 100 noivas pela primeira vez e 53 respondem que elas são mais jovens do que seus noivos. Para o teste de hipótese, ela usa um nível de significância de 1%.

Resposta

Configure o teste de hipótese:

O nível de significância de 1% significa que α = 0,01. Este é um teste de uma única proporção populacional.

$H_{0}: p = 0.50$$H_{a}: p \neq 0.50$

As palavras “é igual ou diferente de” indicam que este é um teste bicaudal.

Calcule a distribuição necessária:

Variável aleatória:$P′ =$ a porcentagem de noivas pela primeira vez que são mais jovens que seus noivos.

Distribuição para o teste: O problema não contém nenhuma menção a uma média. As informações são fornecidas em termos de porcentagens. Use a distribuição para P′s, a proporção estimada.

\[P' - N\left(p, \sqrt{\frac{p-q}{n}}\right)\nonumber \]

Portanto,

\[P' - N\left(0.5, \sqrt{\frac{0.5-0.5}{100}}\right)\nonumber \]

onde$p = 0.50, q = 1−p = 0.50$, e$n = 100$

Calcule o valor p usando a distribuição normal para proporções:

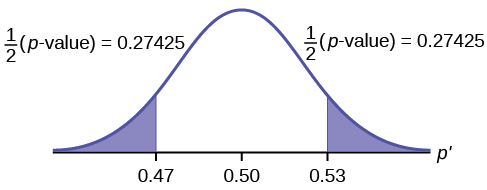
\[p\text{-value} = P(p′ < 0.47 \space or \space p′ > 0.53) = 0.5485\nonumber \]

onde\[x = 53, p' = \frac{x}{n} = \frac{53}{100} = 0.53\nonumber \].

Interpretação do valor p: Se a hipótese nula for verdadeira, há 0,5485 probabilidade (54,85%) de que a proporção da amostra (estimada)$p'$ seja 0,53 ou mais OU 0,47 ou menos (veja o gráfico na Figura).

Curva de distribuição normal da porcentagem de noivas pela primeira vez que são mais jovens que o noivo com valores de 0,47, 0,50 e 0,53 no eixo x. As linhas verticais ascendentes se estendem de 0,47 e 0,53 até a curva. 1/2 (valores de p) são calculados para as áreas externas de 0,47 e 0,53. — Figura$\PageIndex{12}$

$\mu = p = 0.50$vem da$H_{0}$ hipótese nula.

$p′ = 0.53$. Como a curva é simétrica e o teste é bicaudal, o$p′$ para a cauda esquerda é igual a$0.50 – 0.03 = 0.47$ onde$\mu = p = 0.50$. (0,03 é a diferença entre 0,53 e 0,50).

Compare$\alpha$ e o$p\text{-value}$:

Desde$\alpha = 0.01$$p\text{-value} = 0.5485$ e. $\alpha < p\text{-value}$.

Tome uma decisão: desde então$\alpha < p\text{-value}$, você não pode rejeitar$H_{0}$.

Conclusão: No nível de significância de 1%, os dados da amostra não mostram evidências suficientes de que a porcentagem de noivas pela primeira vez que são mais jovens do que seus noivos seja diferente de 50%.

O$p\text{-value}$ pode ser facilmente calculado.

Pressione STAT e vá até TESTS. Pressione 5:1 -PropzTest. Insira .5 para$p_{0}$, 53 para$x$ e 100 para$n$. Seta para baixo até Prop e seta para não é igual$p_{0}$. Pressione ENTER. Seta para baixo até Calcular e pressione ENTER. A calculadora calcula a estatística$p\text{-value}$ ($p = 0.5485$) e a estatística de teste ($z$-score). Prop não é igual a 0,5 é a hipótese alternativa. Faça esse conjunto de instruções novamente, exceto a seta para desenhar (em vez de calcular). Pressione ENTER. Um gráfico sombreado aparece com$z = 0.6$ (estatística de teste) e$p = 0.5485$ ($p\text{-value}$). Ao usar o Draw, certifique-se de que nenhuma outra equação seja destacada$Y =$ e que os gráficos estejam desativados.

Os erros do Tipo I e do Tipo II são os seguintes:

O erro Tipo I é concluir que a proporção de noivas pela primeira vez que são mais jovens do que seus noivos é diferente de 50% quando, na verdade, a proporção é de 50%. (Rejeite a hipótese nula quando a hipótese nula for verdadeira).

O erro do Tipo II é que não há evidências suficientes para concluir que a proporção de noivas pela primeira vez que são mais jovens do que seus noivos difere de 50% quando, na verdade, a proporção difere de 50%. (Não rejeite a hipótese nula quando a hipótese nula for falsa.)

Exercício$\PageIndex{7}$

Um professor acredita que 85% dos alunos da turma vão querer fazer uma excursão ao zoológico local. Ela realiza um teste de hipótese para determinar se a porcentagem é igual ou diferente de 85%. O professor faz uma amostra de 50 alunos e 39 respondem que gostariam de ir ao zoológico. Para o teste de hipótese, use um nível de significância de 1%.

Primeiro, determine que tipo de teste é esse, configure o teste de hipótese, encontre o$p\text{-value}$, esboce o gráfico e declare sua conclusão.

Resposta

Como o problema é sobre porcentagens, este é um teste de proporções de população única.

$H_{0} : p = 0.85$
$H_{a}: p \neq 0.85$
$p = 0.7554$

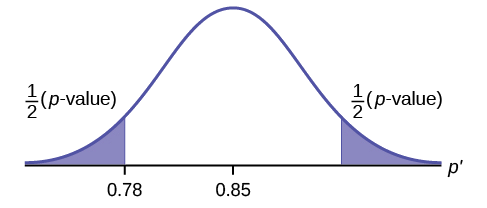
Porque$p > \alpha$ não rejeitamos a hipótese nula. Não há evidências suficientes para sugerir que a proporção de estudantes que querem ir ao zoológico não seja de 85%.

Exemplo$\PageIndex{8}$

Suponha que um grupo de consumidores suspeite que a proporção de famílias que têm três telefones celulares é de 30%. Uma empresa de telefonia celular tem motivos para acreditar que a proporção não é de 30%. Antes de começarem uma grande campanha publicitária, eles realizam um teste de hipótese. Seus profissionais de marketing pesquisam 150 famílias com o resultado de que 43% das famílias têm três telefones celulares.

Resposta

Configure o teste de hipótese:

$H_{0}: p = 0.30, H_{a}: p \neq 0.30$

Determine a distribuição necessária:

A variável aleatória é a$P′ =$ proporção de domicílios que têm três telefones celulares.

A distribuição para o teste de hipótese é$P' - N\left(0.30, \sqrt{\frac{(0.30 \cdot 0.70)}{150}}\right)$

Exercício$\PageIndex{8}$.2

a. O valor que ajuda a determinar o$p\text{-value}$ é$p′$. Calcule$p′$.

Resposta

a.$p' = \frac{x}{n}$ onde$x$ é o número de sucessos e$n$ é o número total na amostra.

$x = 43, n = 150$

$p′ = 43150$

Exercício$\PageIndex{8}$.3

b. O que é um sucesso para esse problema?

Resposta

b. Um sucesso é ter três telefones celulares em uma casa.

Exercício$\PageIndex{8}$.4

c. Qual é o nível de significância?

Resposta

c. O nível de significância é o predefinido$\alpha$. Uma vez que não$\alpha$ é dado, suponha que$\alpha = 0.05$.

Exercício$\PageIndex{8}$.5

d. Desenhe o gráfico para esse problema. Desenhe o eixo horizontal. Etiquete e tonifique adequadamente.

Calcule$p\text{-value}$ o.

Resposta

d.$p\text{-value} = 0.7216$

Exercício$\PageIndex{8}$.6

e. Tome uma decisão. _____________ (Rejeitar/Não rejeitar)$H_{0}$ porque____________.

Resposta

e. Supondo que$\alpha = 0.05, \alpha < p\text{-value}$. A decisão é não rejeitar$H_{0}$ porque não há evidências suficientes para concluir que a proporção de domicílios que têm três telefones celulares não é de 30%.

Exercício$\PageIndex{8}$

Os profissionais de marketing acreditam que 92% dos adultos nos Estados Unidos possuem um telefone celular. Um fabricante de telefones celulares acredita que esse número é realmente menor. 200 adultos americanos são pesquisados, dos quais, 174 relatam ter telefones celulares. Use um nível de significância de 5%. Declare a hipótese nula e alternativa, encontre o valor p, declare sua conclusão e identifique os erros do Tipo I e do Tipo II.

Resposta

$H_{0}: p = 0.92$
$H_{a}: p < 0.92$
$p\text{-value} = 0.0046$

Porque$p < 0.05$ rejeitamos a hipótese nula. Há evidências suficientes para concluir que menos de 92% dos adultos americanos possuem telefones celulares.

Erro tipo I: Concluir que menos de 92% dos adultos americanos possuem telefones celulares quando, na verdade, 92% dos adultos americanos possuem telefones celulares (rejeite a hipótese nula quando a hipótese nula for verdadeira).
Erro tipo II: Concluir que 92% dos adultos americanos possuem telefones celulares quando, na verdade, menos de 92% dos adultos americanos possuem telefones celulares (não rejeite a hipótese nula quando a hipótese nula é falsa).

O exemplo a seguir é um poema escrito por uma estudante de estatística chamada Nicole Hart. A solução para o problema segue o poema. Observe que o teste de hipótese é para uma única proporção da população. Isso significa que as hipóteses nula e alternativa usam o parâmetro$p$. A distribuição do teste é normal. A proporção estimada$p′$ é a proporção de pulgas mortas em relação ao total de pulgas encontradas em Fido. Esta é uma amostra de informação. O problema fornece um cálculo preconcebido$\alpha = 0.01$, para comparação, e de intervalo de confiança de 95%. O poema é inteligente e engraçado, então, por favor, divirta-se!

Exemplo$\PageIndex{9}$

Meu cachorro tem tantas pulgas,

Eles não saem com facilidade.
Quanto ao xampu, já experimentei vários tipos,
até mesmo um chamado Bubble Hype,
que só matou 25% das pulgas,
infelizmente não fiquei satisfeita.

Eu usei todos os tipos de sabonete,
até perder as esperanças.
Até que
um dia vi um anúncio que me surpreendeu.

Um shampoo usado para cães
chamado GOOD ENOUGH to Clean a Hog
Garantido para matar mais pulgas.

Dei banho em Fido
e depois de fazer as contas,
seu número de pulgas
começou a cair em 3!
Antes de seu xampu
eu contei 42.

No final do banho dele,
eu refiz as contas
e o novo xampu matou 17 pulgas.
Então, agora eu estava satisfeito.

Agora é hora de você se divertir.
Com o nível de significância sendo 0,01,
você deve me ajudar a descobrir

Usar o novo xampu ou ficar sem?

Resposta

Configure o teste de hipótese:

$H_{0}: p \leq 0.25$$H_{a}: p > 0.25$

Determine a distribuição necessária:

Em palavras, indique CLARAMENTE o que sua variável$\bar{X}$ aleatória$P′$ representa.

$P′ =$A proporção de pulgas que são mortas pelo novo xampu

Indique a distribuição a ser usada no teste.

Normal:

\[N\left(0.25, \sqrt{\frac{(0.25){1-0.25}}{42}}\right)\nonumber \]

Estatística do teste:$z = 2.3163$

Calcule o$p\text{-value}$ usando a distribuição normal para proporções:

\[p\text{-value} = 0.0103\nonumber \]

Em uma a duas frases completas, explique o valor p significa para esse problema.

Se a hipótese nula for verdadeira (a proporção é 0,25), então há uma probabilidade de 0,0103 de que a proporção da amostra (estimada) seja 0,4048$\left(\frac{17}{42}\right)$ ou mais.

Use as informações anteriores para esboçar uma imagem dessa situação. CLARAMENTE, rotule e dimensione o eixo horizontal e sombreie as regiões correspondentes ao$p\text{-value}$.

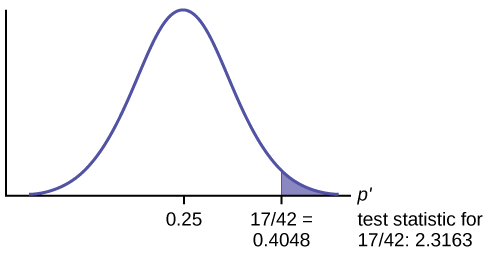
Gráfico de distribuição normal da proporção de pulgas mortas pelo novo xampu com valores de 0,25 e 0,4048 no eixo x. Uma linha vertical ascendente se estende de 0,4048 até a curva e a área à esquerda dela é sombreada. A estatística de teste da proporção da amostra está listada. — Figura$\PageIndex{14}$

Compare$\alpha$ e o$p\text{-value}$:

Indique a decisão correta (“rejeite” ou “não rejeite” a hipótese nula), o motivo dela e escreva uma conclusão apropriada, usando frases completas.

alfa	decisão	motivo da decisão
0,01	Não rejeite$H_{0}$	$\alpha < p\text{-value}$

Conclusão: No nível de significância de 1%, os dados da amostra não mostram evidências suficientes de que a porcentagem de pulgas que são mortas pelo novo xampu seja superior a 25%.

Construa um intervalo de confiança de 95% para a média ou proporção verdadeira. Inclua um esboço do gráfico da situação. Identifique a estimativa pontual e os limites inferior e superior do intervalo de confiança.

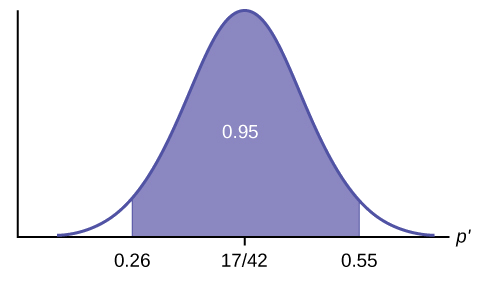
Gráfico de distribuição normal da proporção de pulgas mortas pelo novo xampu com valores de 0,26, 17/42 e 0,55 no eixo x. Uma linha vertical ascendente se estende de 0,26 e 0,55. A área entre esses dois pontos é igual a 0,95. — Figura$\PageIndex{15}$

Intervalo de confiança: (0,26,0,55) Temos 95% de confiança de que a proporção real da população p de pulgas que são mortas pelo novo xampu está entre 26% e 55%.

O resultado desse teste não é muito definitivo, pois$p\text{-value}$ está muito próximo do alfa. Na realidade, provavelmente alguém faria mais testes dando outro banho no cachorro depois que as pulgas tivessem a chance de retornar.

Exemplo$\PageIndex{10}$

O Instituto Nacional de Padrões e Tecnologia fornece dados exatos sobre as propriedades de condutividade dos materiais. A seguir estão as medições de condutividade para 11 peças selecionadas aleatoriamente de um determinado tipo de vidro.

1,11; 1,07; 1,11; 1,07; 1,12; 1,08; 9,8; 1,02; 9,5; 9,5

Há evidências convincentes de que a condutividade média desse tipo de vidro é maior que um? Use um nível de significância de 0,05. Suponha que a população seja normal.

Resposta

Vamos seguir um processo de quatro etapas para responder a essa pergunta estatística.

Indique a pergunta: Precisamos determinar se, em um nível de significância de 0,05, a condutividade média do vidro selecionado é maior que um. Nossas hipóteses serão
1. $H_{0}: \mu \leq 1$
2. $H_{a}: \mu > 1$
Plano: Estamos testando uma média amostral sem um desvio padrão populacional conhecido. Portanto, precisamos usar uma distribuição T de Student. Suponha que a população subjacente seja normal.
Faça os cálculos: Vamos inserir os dados da amostra no TI-83 da seguinte forma.

4. Declare as conclusões: Como o$p\text{-value} (p = 0.036)$ é menor que nosso valor alfa, rejeitaremos a hipótese nula. É razoável afirmar que os dados apoiam a afirmação de que o nível médio de condutividade é maior que um.

Exemplo$\PageIndex{11}$

Em um estudo com 420.019 usuários de telefones celulares, 172 dos indivíduos desenvolveram câncer no cérebro. Teste a alegação de que usuários de telefones celulares desenvolveram câncer cerebral em uma taxa maior do que a de usuários de telefones não celulares (a taxa de câncer cerebral para usuários que não usam telefones celulares é de 0,0340%). Como esse é um problema crítico, use um nível de significância de 0,005. Explique por que o nível de significância deve ser tão baixo em termos de um erro do Tipo I.

Resposta

Seguiremos o processo de quatro etapas.

Precisamos realizar um teste de hipótese sobre a taxa de câncer alegada. Nossas hipóteses serão
1. $H_{0}: p \leq 0.00034$
2. $H_{a}: p > 0.00034$
Se cometermos um erro do Tipo I, estamos basicamente aceitando uma afirmação falsa. Como a alegação descreve ambientes causadores de câncer, queremos minimizar as chances de identificar incorretamente as causas do câncer.
Estaremos testando uma proporção de amostra com$x = 172$$n = 420,019$ e. A amostra é suficientemente grande porque temos$np = 420,019(0.00034) = 142.8$ dois resultados independentes e uma probabilidade fixa de sucesso$p = 0.00034$.$nq = 420,019(0.99966) = 419,876.2$ Assim, poderemos generalizar nossos resultados para a população.
Os resultados de TI associados são

Figura$\PageIndex{11}$.

Figura$\PageIndex{12}$.
Como o$p\text{-value} = 0.0073$ é maior do que nosso valor alfa$= 0.005$, não podemos rejeitar o nulo. Portanto, concluímos que não há evidências suficientes para apoiar a alegação de maiores taxas de câncer cerebral para os usuários de telefones celulares.

Exemplo$\PageIndex{12}$

De acordo com o Censo dos EUA, existem aproximadamente 268.608.618 residentes com 12 anos ou mais. Estatísticas da Rede Nacional de Estupro, Abuso e Incesto indicam que, em média, 207.754 estupros ocorrem a cada ano (homens e mulheres) para pessoas com 12 anos ou mais. Isso se traduz em uma porcentagem de agressões sexuais de 0,078%. No Condado de Daviess, KY, foram relatados 11 estupros para uma população de 37.937. Realize um teste de hipótese apropriado para determinar se há uma diferença estatisticamente significativa entre a porcentagem local de agressão sexual e a porcentagem nacional de agressão sexual. Use um nível de significância de 0,01.

Resposta

Seguiremos o plano de quatro etapas.

Precisamos testar se a proporção de agressões sexuais no Condado de Daviess, KY é significativamente diferente da média nacional.
Como são apresentadas proporções, usaremos um teste z de proporção única. As hipóteses para o teste serão
1. $H_{0}: p = 0.00078$
2. $H_{a}: p \neq 0.00078$
As capturas de tela a seguir exibem as estatísticas resumidas do teste de hipótese.

Figura$\PageIndex{13}$.

Figura$\PageIndex{14}$.
Como o$p\text{-value}$,$p = 0.00063$, é menor que o nível alfa de 0,01, os dados da amostra indicam que devemos rejeitar a hipótese nula. Em conclusão, os dados da amostra apoiam a alegação de que a proporção de agressões sexuais no Condado de Daviess, Kentucky, é diferente da proporção média nacional.

Revisão

O teste de hipótese em si tem um processo estabelecido. Isso pode ser resumido da seguinte forma:

Determine$H_{0}$$H_{a}$ e. Lembre-se de que eles são contraditórios.
Determine a variável aleatória.
Determine a distribuição do teste.
Desenhe um gráfico, calcule a estatística de teste e use a estatística de teste para calcular$p\text{-value}$ o. (Uma pontuação z e uma pontuação t são exemplos de estatísticas de teste.)
Compare o α preconcebido com o valor p, tome uma decisão (rejeite ou não rejeite H ₀) e escreva uma conclusão clara usando frases em inglês.

Observe que, ao realizar o teste de hipótese, você usa$\alpha$ e não$\beta$. $\beta$é necessário para ajudar a determinar o tamanho da amostra dos dados usados no cálculo do$p\text{-value}$. Lembre-se de que a quantidade$1 – \beta$ é chamada de Potência do Teste. Uma alta potência é desejável. Se o poder for muito baixo, os estatísticos normalmente aumentam o tamanho da amostra, mantendo α o mesmo. Se o poder for baixo, a hipótese nula pode não ser rejeitada quando deveria ser.

Exercício$\PageIndex{8}$

Suponha$H_{0}: \mu = 9$$H_{a}: \mu < 9$ e. É um teste de cauda esquerda, cauda direita ou bicaudal?

Resposta

Este é um teste com cauda esquerda.

Exercício$\PageIndex{9}$

Suponha$H_{0}: \mu \leq 6$$H_{a}: \mu > 6$ e. É um teste de cauda esquerda, cauda direita ou bicaudal?

Exercício$\PageIndex{10}$

Suponha$H_{0}: p = 0.25$$H_{a}: p \neq 0.25$ e. É um teste de cauda esquerda, cauda direita ou bicaudal?

Resposta

Este é um teste bicaudal.

Exercício$\PageIndex{11}$

Desenhe o gráfico geral de um teste com cauda esquerda.

Exercício$\PageIndex{12}$

Desenhe o gráfico de um teste bicaudal.

Resposta

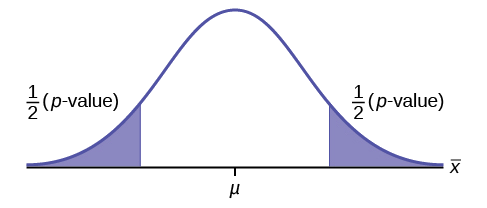
Exercício$\PageIndex{13}$

Uma garrafa de água é rotulada como contendo 16 onças fluidas de água. Você acredita que é menos do que isso. Que tipo de teste você usaria?

Exercício$\PageIndex{14}$

Seu amigo afirma que sua pontuação média no golfe é 63. Você quer mostrar que é maior do que isso. Que tipo de teste você usaria?

Resposta

um teste com cauda direita

Exercício$\PageIndex{15}$

Uma balança de banheiro afirma ser capaz de identificar corretamente qualquer peso dentro de meio quilo. Você acha que não pode ser tão preciso. Que tipo de teste você usaria?

Exercício$\PageIndex{16}$

Você joga uma moeda e registra se ela mostra cabeças ou caudas. Você sabe que a probabilidade de ganhar cabeças é de 50%, mas acha que é menor para essa moeda em particular. Que tipo de teste você usaria?

Resposta

um teste com cauda esquerda

Exercício$\PageIndex{17}$

Se a hipótese alternativa tiver um símbolo não igual a ($\neq$), você sabe usar qual tipo de teste?

Exercício$\PageIndex{18}$

Suponha que a hipótese nula afirme que a média é de pelo menos 18. É um teste de cauda esquerda, cauda direita ou bicaudal?

Resposta

Este é um teste com cauda esquerda.

Exercício$\PageIndex{19}$

Suponha que a hipótese nula afirme que a média é no máximo 12. É um teste de cauda esquerda, cauda direita ou bicaudal?

Exercício$\PageIndex{20}$

Suponha que a hipótese nula afirme que a média é igual a 88. A hipótese alternativa afirma que a média não é igual a 88. É um teste de cauda esquerda, cauda direita ou bicaudal?

Resposta

Este é um teste bicaudal.

Referências

Dados de Amit Schitai. Diretor de Tecnologia Instrucional e Ensino à Distância. LBCC.
Dados da Bloomberg Businessweek. Disponível on-line em www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
Dados de energy.gov. Disponível on-line em http://energy.gov (acessado em 27 de junho de 2013).
Dados do Gallup®. Disponível on-line em www.gallup.com (acessado em 27 de junho de 2013).
Dados de Growing by Degrees, de Allen e Seaman.
Dados da La Leche League International. Disponível on-line em www.lalecheleague.org/law/BAFEB01.html.
Dados da American Automobile Association. Disponível on-line em www.aaa.com (acessado em 27 de junho de 2013).
Dados da American Library Association. Disponível on-line em www.ala.org (acessado em 27 de junho de 2013).
Dados do Bureau of Labor Statistics Disponível on-line em http://www.bls.gov/oes/current/oes291111.htm.
Dados dos Centros de Controle e Prevenção de Doenças. Disponível on-line em www.cdc.gov (acessado em 27 de junho de 2013)
Dados do Departamento de Censo dos EUA, disponíveis on-line em quickfacts.census.gov/qfd/states 00000.html (acessado em 27 de junho de 2013).
Dados do Departamento de Censo dos Estados Unidos. Disponível on-line em www.census.gov/hhes/socdemo/language/.
Dados da Toastmasters International. Disponível on-line em http://toastmasters.org/artisan/deta...eID=429&Page=1.
Dados do Weather Underground. Disponível on-line em www.wunderground.com (acessado em 27 de junho de 2013).
Departamento Federal de Investigações. “Relatórios uniformes de crimes e índice de crimes em Daviess, no estado de Kentucky, aplicados pelo Condado de Daviess de 1985 a 2005.” Disponível on-line em http://www.disastercenter.com/kentucky/crime/3868.htm (acessado em 27 de junho de 2013).
“Distrito da Faculdade Comunitária de Foothill-De Anza”. De Anza College, inverno de 2006. Disponível on-line em research.fhda.edu/factbook/DA... t_da_2006w.pdf.
Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Telefones celulares e câncer — um estudo de coorte nacional na Dinamarca.” Instituto de Epidemiologia do Câncer e Sociedade Dinamarquesa do Câncer, 93 (3) :203-7. Disponível on-line em http://www.ncbi.nlm.nih.gov/pubmed/11158188 (acessado em 27 de junho de 2013).
Rede Nacional de Estupro, Abuso e Incesto. “Com que frequência a agressão sexual ocorre?” CHUVA, 2009. Disponível on-line em www.rainn.org/get-information... sexual-assault (acessado em 27 de junho de 2013).

Glossário

Teorema do limite central: Dada uma variável aleatória (VR) com média conhecida$\mu$ e desvio padrão conhecido$\sigma$. Estamos amostrando com tamanho$n$ e estamos interessados em dois novos RVs - a média da amostra e a soma da amostra$\sum X$.$\bar{X}$ Se o tamanho$n$ da amostra for suficientemente grande, então$\bar{X} - N\left(\mu, \frac{\sigma}{\sqrt{n}}\right)$$\sum X - N \left(n\mu, \sqrt{n}\sigma\right)$ e. Se o tamanho n da amostra for suficientemente grande, a distribuição das médias da amostra e a distribuição das somas da amostra se aproximarão de uma distribuição normal, independentemente da forma da população. A média das médias da amostra será igual à média da população e a média das somas da amostra será igual$n$ à média da população. O desvio padrão da distribuição das médias da amostra,$\frac{\sigma}{\sqrt{n}}$, é chamado de erro padrão da média.