9.5: Eventos raros, amostra, decisão e conclusão

Last updated
Save as PDF

Page ID: 190257

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Estabelecer o tipo de distribuição, o tamanho da amostra e o desvio padrão conhecido ou desconhecido pode ajudar você a descobrir como fazer um teste de hipótese. No entanto, há vários outros fatores que você deve considerar ao elaborar um teste de hipótese.

Eventos raros

Suponha que você faça uma suposição sobre uma propriedade da população (essa suposição é a hipótese nula). Em seguida, você coleta dados de amostra aleatoriamente. Se a amostra tiver propriedades que seriam muito improváveis de ocorrer se a suposição fosse verdadeira, você concluiria que sua suposição sobre a população provavelmente está incorreta. (Lembre-se de que sua suposição é apenas uma suposição — não é um fato e pode ou não ser verdadeira. Mas seus dados de amostra são reais e mostram um fato que parece contradizer sua suposição.)

Por exemplo, Didi e Ali estão na festa de aniversário de um amigo muito rico. Eles se apressam em ser os primeiros na fila para pegar um prêmio em uma cesta alta que não conseguem ver por dentro porque estarão com os olhos vendados. Há 200 bolhas de plástico na cesta e Didi e Ali foram informados de que há apenas uma com uma nota de $100. Didi é a primeira pessoa a enfiar a mão na cesta e puxar uma bolha. Sua bolha contém uma nota de $100. A probabilidade de isso acontecer é$\frac{1}{200} = 0.005$. Como isso é tão improvável, Ali espera que o que lhes foi dito esteja errado e que haja mais notas de $100 na cesta. Um “evento raro” ocorreu (Didi recebendo a nota de $100), então Ali duvida da suposição de que apenas uma nota de $100 esteja na cesta.

Usando a amostra para testar a hipótese nula

Use os dados da amostra para calcular a probabilidade real de obter o resultado do teste, chamada$p$ de valor. O$p$ valor -é a probabilidade de que, se a hipótese nula for verdadeira, os resultados de outra amostra selecionada aleatoriamente sejam tão extremos ou mais extremos quanto os resultados obtidos da amostra dada.

Um grande$p$ valor calculado a partir dos dados indica que não devemos rejeitar a hipótese nula. Quanto menor o$p$ valor -, mais improvável é o resultado e mais forte é a evidência contra a hipótese nula. Rejeitaríamos a hipótese nula se a evidência fosse fortemente contra ela.

Desenhe um gráfico que mostre o$p$ valor -. O teste de hipótese é mais fácil de realizar se você usar um gráfico porque vê o problema com mais clareza.

Exemplo$\PageIndex{1}$

Suponha que um padeiro afirme que a altura do pão é superior a 15 cm, em média. Vários de seus clientes não acreditam nele. Para convencer seus clientes de que ele está certo, o padeiro decide fazer um teste de hipótese. Ele faz 10 pães. A altura média dos pães da amostra é de 17 cm. O padeiro sabe, ao assar centenas de pães, que o desvio padrão para a altura é de 0,5 cm. e a distribuição das alturas é normal.

A hipótese nula pode ser$H_{0}: \mu \leq 15$
A hipótese alternativa é$H_{a}: \mu > 15$

As palavras “é mais que” se traduzem como$>$ "" então$\mu > 15$ "" entra na hipótese alternativa. A hipótese nula deve contradizer a hipótese alternativa.

Como$\sigma$ é conhecido ($\sigma = 0.5 cm.$), sabe-se que a distribuição da população é normal com média$μ = 15$ e desvio padrão

\[\dfrac{\sigma}{\sqrt{n}} = \frac{0.5}{\sqrt{10}} = 0.16. \nonumber\]

Suponha que a hipótese nula seja verdadeira (a altura média dos pães não seja superior a 15 cm). Então, a altura média (17 cm) calculada a partir da amostra é inesperadamente grande? O teste de hipótese funciona perguntando o quão improvável seria a média da amostra se a hipótese nula fosse verdadeira. O gráfico mostra a distância entre a média da amostra na curva normal. O valor p é a probabilidade de que, se coletássemos outras amostras, qualquer outra média amostral cairia pelo menos até 17 cm.

O$p$ valor -, então, é a probabilidade de que uma média amostral seja igual ou maior que 17 cm. quando a média da população é, na verdade, 15 cm. Podemos calcular essa probabilidade usando a distribuição normal para médias.

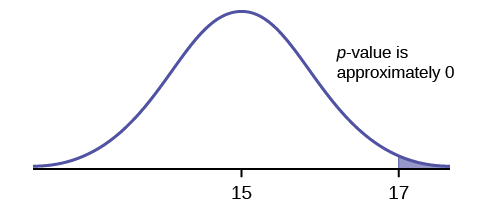
$p\text{-value} = P(\bar{x} > 17)$que é aproximadamente zero.

Um$p$ valor de aproximadamente zero nos diz que é altamente improvável que um pedaço de pão não ultrapasse 15 cm, em média. Ou seja, quase 0% de todos os pães teriam pelo menos 17 cm de altura. puramente por ACASO se a altura média da população fosse realmente de 15 cm. Como o resultado de 17 cm é muito improvável (o que significa que não está acontecendo apenas por acaso), concluímos que a evidência é fortemente contra a hipótese nula (a altura média é de no máximo 15 cm). Há evidências suficientes de que a altura média real da população dos pães do padeiro é maior que 15 cm.

Exercício$\PageIndex{1}$

Uma distribuição normal tem um desvio padrão de 1. Queremos verificar uma afirmação de que a média é maior que 12. Uma amostra de 36 é coletada com uma média amostral de 12,5.

$H_{0}: \mu \leq 12$
$H_{a}: \mu > 12$

O$p$ valor -é 0,0013

Desenhe um gráfico que mostre o$p$ valor -.

Responda: $p\text{-value} = 0.0013$

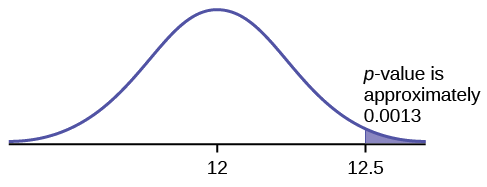
Figura$\PageIndex{2}$

Decisão e conclusão

Uma forma sistemática de tomar a decisão de rejeitar ou não a hipótese nula é comparar o$p$ valor -com um predefinido ou preconcebido$\alpha$ (também chamado de "nível de significância “). Uma predefinição$\alpha$ é a probabilidade de um erro do Tipo I (rejeitar a hipótese nula quando a hipótese nula é verdadeira). Ele pode ou não ser dado a você no início do problema.

Ao tomar a decisão de rejeitar ou não rejeitar$H_{0}$, faça o seguinte:

Se$\alpha > p\text{-value}$, rejeite$H_{0}$. Os resultados dos dados da amostra são significativos. Há evidências suficientes para concluir que$H_{0}$ é uma crença incorreta e que a hipótese alternativa,$H_{a}$, pode estar correta.
Se sim$\alpha \leq p\text{-value}$, não rejeite$H_{0}$. Os resultados dos dados da amostra não são significativos. Não há evidências suficientes para concluir que a hipótese alternativa,$H_{a}$, possa estar correta.

Quando você “não rejeita$H_{0}$ “, isso não significa que você deva acreditar que H ₀ é verdadeiro. Significa simplesmente que os dados da amostra falharam em fornecer evidências suficientes para lançar sérias dúvidas sobre a veracidade do$H_{0}$.

Conclusão: Depois de tomar sua decisão, escreva uma conclusão cuidadosa sobre as hipóteses em termos do problema dado.

Exemplo$\PageIndex{2}$

Ao usar o$p$ valor -para avaliar um teste de hipótese, às vezes é útil usar o seguinte dispositivo de memória

Se o$p$ valor -for baixo, o nulo deverá ser válido.
Se o$p$ valor -for alto, o nulo deverá voar.

Esse auxílio de memória relaciona um$p$ valor -menor que o alfa estabelecido (o$p$ é baixo) como rejeitando a hipótese nula e, da mesma forma, relaciona um$p$ valor -maior que o alfa estabelecido (o$p$ é alto) como não rejeitando a hipótese nula.

Preencha os espaços em branco.

Rejeite a hipótese nula quando __________________________________.

Os resultados dos dados da amostra _____________________________________.

Não rejeite a hipótese nula quando __________________________________________.

Os resultados dos dados da amostra ________________________________________.

Responda

Rejeite a hipótese nula quando o$p$ valor -for menor que o valor alfa estabelecido. Os resultados dos dados da amostra apoiam a hipótese alternativa.

Não rejeite a hipótese nula quando o$p$ valor -for maior do que o valor alfa estabelecido. Os resultados dos dados da amostra não apoiam a hipótese alternativa.

Exercício$\PageIndex{2}$

O It's a Boy Genetics Labs afirma que seus procedimentos aumentam as chances de um menino nascer. Os resultados de um teste de uma única proporção populacional são os seguintes:

$H_{0}: p = 0.50, H_{a}: p > 0.50$
$\alpha = 0.01$
$p\text{-value} = 0.025$

Interprete os resultados e declare uma conclusão em termos simples e não técnicos.

Responda: Como o$p$ valor -é maior do que o valor alfa estabelecido (o$p$ valor -é alto), não rejeitamos a hipótese nula. Não há evidências suficientes para apoiar a alegação declarada do It's a Boy Genetics Labs de que seus procedimentos aumentam as chances de um menino nascer.

Revisão

Quando a probabilidade de um evento ocorrer é baixa e isso acontece, isso é chamado de evento raro. É importante considerar eventos raros em testes de hipóteses porque eles podem informar sua disposição de não rejeitar ou rejeitar uma hipótese nula. Para testar uma hipótese nula, encontre o valor p para os dados da amostra e represente graficamente os resultados. Ao decidir se deve ou não rejeitar a hipótese nula, lembre-se desses dois parâmetros:

$\alpha > p-value$, rejeite a hipótese nula
$\alpha \leq p-value$, não rejeite a hipótese nula

Glossário

Nível de significância do teste: probabilidade de um erro do Tipo I (rejeite a hipótese nula quando ela for verdadeira). Notação:$\alpha$. No teste de hipóteses, o Nível de Significância é chamado de preconcebido$\alpha$ ou predefinido$\alpha$.

$p$-valor: a probabilidade de que um evento aconteça puramente por acaso, assumindo que a hipótese nula é verdadeira. Quanto menor o$p$ valor -, mais forte é a evidência contra a hipótese nula.