7.3: O teorema do limite central para somas

Last updated
Save as PDF

Page ID: 190383

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Suponha que\(X\) seja uma variável aleatória com uma distribuição que pode ser conhecida ou desconhecida (pode ser qualquer distribuição) e suponha que:

\(\mu_{x}\)= a média de\(X\)
\(\sigma_{x}\)= o desvio padrão de\(X\)

Se você desenhar amostras aleatórias de tamanho\(n\), à medida que\(n\) aumenta, a variável aleatória\(\sum X\) que consiste em somas tende a ser distribuída normalmente e

\[\sum X \sim N((n)(\mu_{x}), (\sqrt{n})(\sigma_{x})).\]

O teorema do limite central para somas diz que, se você continuar desenhando amostras cada vez maiores e obtendo suas somas, as somas formam sua própria distribuição normal (a distribuição amostral), que se aproxima de uma distribuição normal à medida que o tamanho da amostra aumenta. A distribuição normal tem uma média igual à média original multiplicada pelo tamanho da amostra e um desvio padrão igual ao desvio padrão original multiplicado pela raiz quadrada do tamanho da amostra.

A variável aleatória\(\sum X\) tem a seguinte pontuação z associada a ela:

\(\sum x\)é uma soma.
\(z = \frac{\sum x - (n)(\mu_{x})}{(\sqrt{n})(\sigma_{x})}\)
1. \((n)(\mu_{x})\)= a média de\(\sum X\)
2. \((\sqrt{n})(\sigma_{x})\)= desvio padrão de\(\sum X\)

Calculadora

Para encontrar probabilidades de somas na calculadora, siga estas etapas.

2 ^e DISTR

2: normalcdf normalcdf (valor inferior da área, valor superior da área, (\(n\)) (média), (\(\sqrt{n}\)) (desvio padrão))

onde:

média é a média da distribuição original
desvio padrão é o desvio padrão da distribuição original
tamanho da amostra\(= n\)

Exemplo\(\PageIndex{1}\)

Uma distribuição desconhecida tem uma média de 90 e um desvio padrão de 15. Uma amostra de tamanho 80 é retirada aleatoriamente da população.

Determine a probabilidade de que a soma dos 80 valores (ou o total dos 80 valores) seja maior que 7.500.
Encontre a soma que é 1,5 desvio padrão acima da média das somas.

Responda

Deixe\(X =\) um valor da população desconhecida original. A pergunta de probabilidade pede que você encontre uma probabilidade para a soma (ou total de) 80 valores.

\(\sum X =\)a soma ou o total de 80 valores. Uma vez que\(\mu_{x} = 90\)\(\sigma_{x} = 15\),, e\(n = 80\),\(\sum X \sim N((80)(90),(\sqrt{80})(15))\)

média das somas\(= (n)(\mu_{x}) = (80)(90) = 7,200\)
desvio padrão das somas\(= (\sqrt{n})(\sigma_{x}) = (\sqrt{80})(15) = (80)(15)\)
soma de 80 valores\(= \sum X = 7,500\)

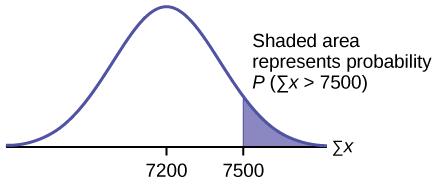
a. Encontre\(P(\sum X > 7,500)\)

\(P(\sum X > 7,500) = 0.0127\)

Essa é uma curva de distribuição normal. O pico da curva coincide com o ponto 7200 no eixo horizontal. O ponto 7500 também é rotulado. Uma linha vertical se estende do ponto 7500 até a curva. A área à direita de 7500 abaixo da curva está sombreada. — Figura\(\PageIndex{1}\).

normalcdf (valor inferior, valor superior, média das somas, stdev das somas)

A lista de parâmetros é abreviada\(\left(lower, upper, (n)(\mu_{x}, (\sqrt{n}(\sigma_{x})\right)\)

cdf normal\(\left(7500,1E99,(80)(90),(\sqrt{80})(15)\right) = 0.0127\)

LEMBRETE

E99 = 10 ⁹⁹.

Pressione a tecla EE para E.

b. Descubra\(\sum x\) onde\(z = 1.5\).

\(\sum x = (n)(\nu_{x}) + (z)(\sqrt{n})(\sigma_{x}) = (80)(90) + (1.5)(\sqrt{80})(15) = 7,401.2\)

Exercício\(\PageIndex{1}\)

Uma distribuição desconhecida tem uma média de 45 e um desvio padrão de oito. Um tamanho amostral de 50 é retirado aleatoriamente da população. Determine a probabilidade de que a soma dos 50 valores seja maior que 2.400.

Responda

0,0040

Calculadora

Para encontrar os percentis das somas na calculadora, siga estas etapas.

2 ^e DiStr

3: Norma INV

\(k = \text{invNorm} (\text{area to the left of} k, (n)(\text{mean}), (\sqrt{n})(\text{standard deviation}))\)

onde:

\(k\)é o\(k\) ^décimo percentil
média é a média da distribuição original
desvio padrão é o desvio padrão da distribuição original
tamanho da amostra\(= n\)

Exemplo\(\PageIndex{2}\)

Em um estudo recente publicado em 29 de outubro de 2012 no Flurry Blog, a idade média dos usuários de tablets é de 34 anos. Suponha que o desvio padrão seja de 15 anos. A amostra de tamanho é 50.

Quais são a média e o desvio padrão para a soma das idades dos usuários de tablets? Qual é a distribuição?
Determine a probabilidade de que a soma das idades esteja entre 1.500 e 1.800 anos.
Encontre o ^80º percentil para a soma das 50 idades.

Responda

\(\mu_{x} - n\mu_{x} = 1,700\)e\(\sigma_{\sum X} = \sqrt{n}\sigma_{X} = (\sqrt{50})(15) = 106.01\)
A distribuição é normal para somas pelo teorema do limite central.
\(P(1500 < \sum X < 1800) = (1,500, 1,800, (50)(34), (\sqrt{50})(15)) = 0.7974\)
Seja\(k\) = o ^80º percentil.
\(k = (0.80,(50)(34),(\sqrt{50})(15)) = 1,789.3\)

Exercício\(\PageIndex{2}\)

Em um estudo recente publicado em 29 de outubro de 2012 no Flurry Blog, a idade média dos usuários de tablets é de 35 anos. Suponha que o desvio padrão seja de dez anos. O tamanho da amostra é 39.

Quais são a média e o desvio padrão para a soma das idades dos usuários de tablets? Qual é a distribuição?
Determine a probabilidade de que a soma das idades esteja entre 1.400 e 1.500 anos.
Encontre o ^90º percentil para a soma das 39 idades.

Responda

\(\mu_{\sum X} = n\mu_{X} = 1,365\)e\(\sigma_{\sum X} = \sqrt{n}\sigma_{x} = 62.4\)
A distribuição é normal para somas pelo teorema do limite central.
\(P(1400 < \sum_{X} < 1500) = \text{normalcdf} (1400,1500,(39)(35),(\sqrt{39})(10)) = 0.2723\)
Seja\(k\) = o ^90º percentil.
\(k = \text{invNorm} (0.90,(39)(35),(\sqrt{39}) (10)) = 1445.0\)

Exemplo\(\PageIndex{3}\)

O número médio de minutos para o engajamento do aplicativo por um usuário de tablet é de 8,2 minutos. Suponha que o desvio padrão seja de um minuto. Pegue uma amostra do tamanho 70.

Quais são a média e o desvio padrão das somas?
^{Encontre o percentil 95 para a soma da amostra.} Interprete esse valor em uma frase completa.
Determine a probabilidade de que a soma da amostra seja de pelo menos dez horas.

Responda

\(\mu_{\sum X} = n\mu_{X}= 70(8.2) = 574\)minutos e\(\sigma_{\sum X} (\sqrt{n})(\sigma_{x}) = (\sqrt{70})(1) = 8.37\) minutos
^{Seja\(k\) = o percentil 95.}
\(k = \text{invNorm} (0.95,(70)(8.2),(\sqrt{70})(1)) = 587.76\)minutos
Noventa e cinco por cento dos tempos de engajamento do aplicativo são no máximo 587,76 minutos.
dez horas = 600 minutos
\(P(\sum X \geq 600) = \text{normalcdf}(600,E99,(70)(8.2),(\sqrt{70})(1)) = 0.0009\)

Exercício\(\PageIndex{3}\)

O número médio de minutos para engajamento do aplicativo pelo uso de uma tabela é de 8,2 minutos. Suponha que o desvio padrão seja de um minuto. Pegue um tamanho de amostra de 70.

Qual é a probabilidade de que a soma da amostra esteja entre sete horas e dez horas? O que isso significa no contexto do problema?
^{^{Encontre os percentis 84 e 16 para a soma da amostra.}} Interprete esses valores no contexto.

Responda

7 horas = 420 minutos
10 horas = 600 minutos
\(\text{normalcdf} P(420 \leq \sum X \leq 600) = \text{normalcdf}(420,600,(70)(8.2),\sqrt{70}(1)) = 0.9991\)
Isso significa que, para esta amostra de somas, há 99,9% de chance de que a soma dos minutos de uso esteja entre 420 minutos e 600 minutos.
\(\text{invNorm}(0.84,(70)(8.2)\),\(\sqrt{70}(1)) = 582.32\)
\(\text{invNorm}(0.16,(70)(8.2),(\sqrt{70}(1)) = 565.68\)
Como 84% dos tempos de engajamento do aplicativo são no máximo 582,32 minutos e 16% dos tempos de engajamento do aplicativo são no máximo 565,68 minutos, podemos afirmar que 68% dos tempos de engajamento do aplicativo estão entre 565,68 minutos e 582,32 minutos.

Referências

Farago, Peter. “A verdade sobre cães e gatos: diferenças de uso de smartphones e tablets”. O Blog Flurry, 2013. Publicado a 29 de outubro de 2012. Disponível on-line em blog.flurry.com (acessado em 17 de maio de 2013).

Revisão

O teorema do limite central nos diz que, para uma população com qualquer distribuição, a distribuição das somas das médias da amostra se aproxima de uma distribuição normal à medida que o tamanho da amostra aumenta. Em outras palavras, se o tamanho da amostra for grande o suficiente, a distribuição das somas pode ser aproximada por uma distribuição normal, mesmo que a população original não esteja normalmente distribuída. Além disso, se a população original tiver uma média\(\mu_{x}\) e um desvio padrão de\(\sigma_{x}\), a média das somas é\(n\)\(\mu_{x}\) e o desvio padrão é (\(\sqrt{n}\)) (\(\sigma_{x}\)), onde\(n\) é o tamanho da amostra.

Revisão da fórmula

O teorema do limite central para somas:\(\sum X ~ N[(n)(\mu_{x}, (\sqrt{n})(\sigma_{x}))]\)
Média para somas\((\sum X): (n)(\mu_{x})\)
O teorema do limite central para somas\(z\) - pontuação e desvio padrão para somas:\(z \text{ for the sample mean} = \frac{\sum x - (n)(\mu_{x})}{(\sqrt{n})(\sigma_{x})}\)
Desvio padrão para somas\((\sum X): (\sqrt{n})(\sigma_{x})\)