7.4: Usando o Teorema do Limite Central

É importante que você entenda quando usar o teorema do limite central (clt). Se você estiver sendo solicitado a encontrar a probabilidade da média, use o clt para a média. Se você estiver sendo solicitado a encontrar a probabilidade de uma soma ou total, use o clt para somas. Isso também se aplica aos percentis de médias e somas.

Se você estiver sendo solicitado a encontrar a probabilidade de um valor individual, não use o clt. Use a distribuição de sua variável aleatória.

Lei dos Grandes Números

A lei dos grandes números diz que, se você coletar amostras de tamanho cada vez maior de qualquer população, a média\(\bar{x}\) da amostra tende a se aproximar cada vez mais\(\mu\). A partir do teorema do limite central, sabemos que, à medida que\(n\) se torna cada vez maior, as médias da amostra seguem uma distribuição normal. Quanto maior\(n\) for, menor será o desvio padrão. (Lembre-se de que o desvio padrão para\(\bar{X}\) é\(\dfrac{\sigma}{\sqrt{n}}\).) Isso significa que a média da amostra\(\bar{x}\) deve estar próxima da média da população\(\mu\). Podemos dizer que esse\(\mu\) é o valor que a amostra significa que se aproxima à medida que\(n\) aumenta. O teorema do limite central ilustra a lei dos grandes números.

Exemplo\(\PageIndex{1}\)

Um estudo envolvendo estresse é realizado entre os estudantes de um campus universitário. Os escores de estresse seguem uma distribuição uniforme com a menor pontuação de estresse igual a um e a maior igual a cinco. Usando uma amostra de 75 estudantes, encontre:

1. A probabilidade de que a pontuação média de estresse para os 75 estudantes seja menor que dois.
2. ^{O percentil 90 para a pontuação média de estresse para os 75 estudantes.}
3. A probabilidade de que o total dos 75 escores de estresse seja menor que 200.
4. ^{O percentil 90 para a pontuação total de estresse para os 75 estudantes.}

Soluções

Deixe\(X =\) uma pontuação de estresse.

Os problemas a e b pedem que você encontre uma probabilidade ou um percentil para uma média. Os problemas c e d pedem que você encontre uma probabilidade ou um percentil para um total ou uma soma. O tamanho da amostra,\(n\), é igual a 75.

Uma vez que os escores individuais de estresse seguem uma distribuição uniforme,\(X \sim U(1, 5)\) onde\(a = 1\)\(b = 5\) e.

\[\mu_{x} = \dfrac{a+b}{2} = \dfrac{1+5}{2} = 3\]

\[\sigma_{x} = \sqrt{\dfrac{(b-a)^{2}}{12}} = \sqrt{\dfrac{(5-1)^{2}}{12}} = 1.15\]

Para os problemas 1. e 2., deixe\(\bar{X} =\) a pontuação média de estresse para os 75 alunos. Então,

\[\bar{X} \sim N\left(3, \dfrac{1,15}{\sqrt{75}}\right)\]

onde\(n = 75\).

1. Encontre\(P(\bar{x} < 2)\). Desenhe o gráfico.
2. ^{Encontre o percentil 90 para a média de 75 escores de estresse.} Desenhe um gráfico.
3. Encontre\(P(\sum x < 2000)\). Desenhe o gráfico.
4. Encontre o ^90º percentil para o total de 75 pontuações de estresse. Desenhe um gráfico.

Respostas

uma.\(P(\bar{x} < 2) = 0\)

A probabilidade de que a pontuação média de estresse seja menor que dois é cerca de zero.

Figura\(\PageIndex{1}\).

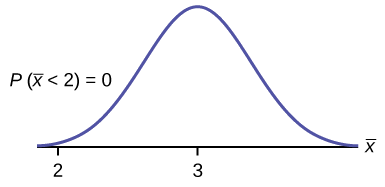
cdf normal\(\left(1,2,3,\dfrac{1.15}{\sqrt{75}}\right) = 0\)

LEMBRETE

A menor pontuação de estresse é uma

b. Deixe\(k =\) o ^90º percentil.

Encontre\(k\), onde\(P(\bar{x} < k) = 0.90\).

\(k = 3.2\)

Figura\(\PageIndex{2}\).

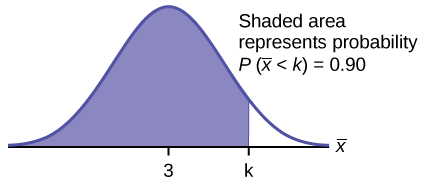
^{O percentil 90 para a média de 75 pontuações é de cerca de 3,2.} Isso nos diz que 90% de todas as médias de 75 escores de estresse são no máximo 3,2 e que 10% são pelo menos 3,2.

Inv Norm\(\left(0.90,3,1.\dfrac{1.15}{\sqrt{75}}\right) = 3.2\)

Para os problemas c e d, deixe\(\sum X =\) a soma dos 75 escores de estresse. Então,

\[\sum X \sim N((75)(3), (\sqrt{75})(1.15))\]

c. A média da soma de 75 escores de estresse é\((75)(3) = 225\)

O desvio padrão da soma de 75 escores de estresse é\((\sqrt{75})(1.15) = 9.96\)

\(P(\sum x < 200)\)

Figura\(\PageIndex{3}\).

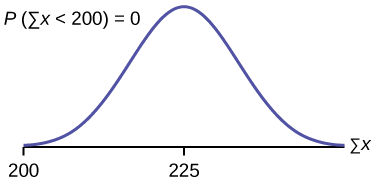
A probabilidade de que o total de 75 pontuações seja menor que 200 é aproximadamente zero.

cdf normal\(75,200,(75)(3),(\sqrt{75})(1.15)\).

LEMBRETE

O menor total de 75 escores de estresse é 75, porque a menor pontuação única é uma.

^{d. Deixe\(k =\) o percentil 90.}

Descubra\(k\) onde\(P(\sum x < k) = 0.90\).

\(k = 237.8\)

Figura\(\PageIndex{4}\).

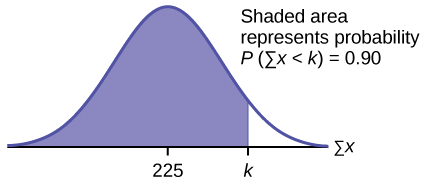
^{O percentil 90 para a soma de 75 pontuações é de cerca de 237,8.} Isso nos diz que 90% de todas as somas de 75 pontuações não são superiores a 237,8 e 10% não são inferiores a 237,8.

Inv Norm\(\left(0.90, (75)(3), (\sqrt{75})(1.15)\right) = 237.8\)

Exercício\(\PageIndex{1}\)

Use as informações em Exemplo\(\PageIndex{1}\), mas use um tamanho de amostra de 55 para responder às seguintes perguntas.

1. Encontre\(P(\bar{x} < 7)\).
2. Encontre\(P(\sum x < 7)\).
3. Encontre o ^80º percentil para a média de 55 pontuações.
4. Encontre o ^85º percentil para a soma das 55 pontuações.

Resposta

1. 0,0265
2. 0,2789
3. 3.13
4. 173,84

Exemplo\(\PageIndex{2}\)

Suponha que um analista de pesquisa de mercado de uma empresa de telefonia celular conduza um estudo de seus clientes que excedem o limite de tempo incluído em seu contrato básico de telefone celular; o analista descobre que, para aquelas pessoas que excedem o tempo incluído em seu contrato básico, o excesso de tempo usado segue um distribuição exponencial com uma média de 22 minutos.

Considere uma amostra aleatória de 80 clientes que excedem o limite de tempo incluído em seu contrato básico de telefone celular.

Deixe\(X =\) o excesso de tempo usado por um cliente de telefone celular INDIVIDUAL que exceda o limite de tempo contratado.

\(X \sim Exp\left(\dfrac{1}{22}\right)\). Dos capítulos anteriores, nós sabemos que\(\mu = 22\)\(\sigma = 22\) e.

Seja\(\bar{X}\) = o excesso de tempo médio usado por uma amostra de\(n = 80\) clientes que excedem o limite de tempo contratado.

\[\bar{X} \sim N\left(22,\dfrac{22}{\sqrt{80}}\right)\]

pelo teorema do limite central para médias amostrais

1. Determine a probabilidade de que o tempo médio de excesso usado pelos 80 clientes na amostra seja maior do que 20 minutos. Isso está nos pedindo que encontremos\(P(\bar{x} > 20)\). Desenhe o gráfico.
2. Suponha que um cliente que exceda o limite de tempo de seu contrato de telefone celular seja selecionado aleatoriamente. Descubra a probabilidade de que o tempo excedente desse cliente individual seja superior a 20 minutos. Isso está nos pedindo que encontremos\(P(x > 20)\).
3. Explique por que as probabilidades nas partes a e b são diferentes.
4. ^{Encontre o percentil 95 para o excesso de tempo médio da amostra para amostras de 80 clientes que excedem seus limites básicos de tempo de contrato.} Desenhe um gráfico.

Resposta

1. Encontre:\(P(\bar{x} > 20)\)

   \(P(\bar{x} > 20) = 0.79199\)usando normalcdf\(\left(20,1\text{E}99,22,\dfrac{22}{\sqrt{80}}\right)\)

   A probabilidade é de 0,7919 de que o tempo médio excedente usado seja superior a 20 minutos, para uma amostra de 80 clientes que excedem o limite de tempo contratado.

   20)." src="https://stats.libretexts.org/@api/de...1180/7.4.5.png">

   Figura\(\PageIndex{5}\).

   LEMBRETE

   1E99 = 10 ⁹⁹ e —1E99 = —10 ⁹⁹. Pressione a tecla EE para E. Ou use apenas 10 ⁹⁹ em vez de 1E99.

2. Encontre\(P(x > 20)\). Lembre-se de usar a distribuição exponencial para um indivíduo:\(X \sim Exp\left(\dfrac{1}{22}\right)\). \(P(x > 20) = e^{(−\left(\dfrac{1}{22}\right)(20))}\)ou\(e^{(–0.04545(20))} = 0.4029\)
3. 1. \(P(x > 20) = 0.4029\)mas\(P(\bar{x} > 20) = 0.7919\)
   2. As probabilidades não são iguais porque usamos distribuições diferentes para calcular a probabilidade para indivíduos e para médias.
   3. Quando solicitado a encontrar a probabilidade de um valor individual, use a distribuição declarada de sua variável aleatória; não use o clt. Use o clt com a distribuição normal quando for solicitado que você encontre a probabilidade de uma média.
4. ^{Seja\(k\) = o percentil 95.} Descubra\(k\) onde\(P(\bar{x} < k) = 0.95\)

   \(k = 26.0\)usando InvNorm\(\left(0.95,22,\dfrac{22}{\sqrt{80}}\right) = 26.0\)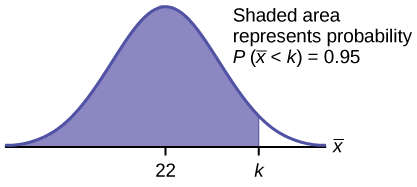

   

   Figura\(\PageIndex{6}\).

   ^{O percentil 95 para o excesso de tempo médio da amostra usado é de cerca de 26,0 minutos para amostras aleatórias de 80 clientes que excedem o tempo contratual permitido.}

   Noventa e cinco por cento dessas amostras teriam médias abaixo de 26 minutos; apenas cinco por cento dessas amostras teriam médias acima de 26 minutos.

Exercício\(\PageIndex{2}\)

Use as informações em Exemplo\(\PageIndex{2}\), mas altere o tamanho da amostra para 144.

1. Encontre\(P(20 < \bar{x} < 30)\).
2. Encontre\(P(\sum x \text{ is at least } 3,000)\).
3. Encontre o ^75º percentil para o excesso de tempo médio da amostra de 144 clientes.
4. Encontre o ^85º percentil para a soma de 144 vezes excedentes usadas pelos clientes.

Resposta

1. 0,8623
2. 0,7377
3. 23,2
4. 3.441,6

Exemplo\(\PageIndex{3}\)

Nos Estados Unidos, alguém é abusado sexualmente a cada dois minutos, em média, de acordo com vários estudos. Suponha que o desvio padrão seja 0,5 minutos e o tamanho da amostra seja 100.

1. Encontre a mediana, o primeiro quartil e o terceiro quartil para a amostra de tempo médio de agressões sexuais nos Estados Unidos.
2. Encontre a mediana, o primeiro quartil e o terceiro quartil para a soma dos tempos de amostra de agressões sexuais nos Estados Unidos.
3. Determine a probabilidade de uma agressão sexual ocorrer em média entre 1,75 e 1,85 minutos.
4. Encontre o valor que é dois desvios padrão acima da média da amostra.
5. Encontre o IQR para a soma dos tempos da amostra.

Resposta

1. Nós temos,\(\mu_{x} = \mu = 2\)\(\sigma_{x} = \dfrac{\sigma}{\sqrt{n}} = \dfrac{0.5}{10} = 0.05\) e. Portanto:
   1. 50 ^º percentil\(= \mu_{x} = \mu = 2\)
   2. ^25º percentil\(= \text{invNorm}(0.25,2,0.05) = 1.97\)
   3. 75 ^º percentil\(= \text{invNorm}(0.75,2,0.05) = 2.03\)
2. Nós temos\(\mu_{\sum X} = n(\mu_{x}) = 100(2)\)\(\sigma_{\mu X} = \sqrt{n}(\sigma_{x}) = 10(0.5) = 5\) e. Portanto
   1. ^{Percentil 50 =}\(\mu_{\sum X} = n(\mu_{X}) = 100(2) = 200\)
   2. ^25º percentil\(= \text{invNorm}(0.25,200,5) = 196.63\)
   3. 75 ^º percentil\(= \text{invNorm}(0.75,200,5) = 203.37\)
3. \(P(1.75 < bar{x} < 1.85) =\)cdf normal\((1.75,1.85,2,0.05) = 0.0013\)
4. Usando a equação\(z\) -score e resolvendo para\(x\), temos\(z = \dfrac{\bar{x} - \mu_{\bar{x}}}{\sigma_{\bar{x}}}\)\(x = 2(0.05) + 2 = 2.1\)
5. O\(IQR\) é 75 ^º percentil — 25 ^º percentil\(= 203.37 – 196.63 = 6.74\)

Exercício\(\PageIndex{3}\)

Com base em dados da Pesquisa Nacional de Saúde, mulheres entre 18 e 24 anos têm uma pressão arterial sistólica média (em mm Hg) de 114,8 com um desvio padrão de 13,1. A pressão arterial sistólica para mulheres entre 18 e 24 anos segue uma distribuição normal.

1. Se uma mulher dessa população for selecionada aleatoriamente, encontre a probabilidade de sua pressão arterial sistólica ser maior que 120.
2. Se 40 mulheres dessa população forem selecionadas aleatoriamente, encontre a probabilidade de que sua pressão arterial sistólica média seja maior que 120.
3. Se a amostra fosse de quatro mulheres entre 18 e 24 anos e não soubéssemos a distribuição original, o teorema do limite central poderia ser usado?

Resposta

1. \(P(x > 120)\)= cdf normal\((120,99,114.8,13.1) = 0.0272\). Há cerca de 3%, que a mulher selecionada aleatoriamente terá pressão arterial sistólica maior que 120.
2. \(P(\bar{x} > 120) =\)cdf normal\(\left(120,114.8,\dfrac{13.1}{\sqrt{40}}\right) = 0.006\). Há apenas 0,6% de chance de que a pressão arterial sistólica média para o grupo selecionado aleatoriamente seja maior que 120.
3. O teorema do limite central não poderia ser usado se o tamanho da amostra fosse quatro e não soubéssemos que a distribuição original era normal. O tamanho da amostra seria muito pequeno.

Exemplo\(\PageIndex{4}\)

Foi feito um estudo sobre a violência contra prostitutas e os sintomas do estresse pós-traumático que elas desenvolveram. A faixa etária das prostitutas era de 14 a 61 anos. A média de idade foi de 30,9 anos com desvio padrão de nove anos.

1. Em uma amostra de 25 prostitutas, qual é a probabilidade de que a idade média das prostitutas seja menor que 35?
2. É provável que a idade média do grupo amostral possa ser superior a 50 anos? Interprete os resultados.
3. Em uma amostra de 49 prostitutas, qual é a probabilidade de que a soma das idades não seja inferior a 1.600?
4. É provável que a soma das idades das 49 prostitutas seja de no máximo 1.595? Interprete os resultados.
5. Encontre o ^95º percentil para a idade média da amostra de 65 prostitutas. Interprete os resultados.
6. ^{Encontre o percentil 90 para a soma das idades de 65 prostitutas.} Interprete os resultados.

Resposta

1. \(P(\bar{x} < 35) =\)cdf normal\((-E99,35,30.9,1.8) = 0.9886\)
2. \(P(\bar{x} > 50) =\)cdf normal\((50, E99,30.9,1.8) \approx 0\). Para esse grupo amostral, é quase impossível que a idade média do grupo seja superior a 50 anos. No entanto, ainda é possível que um indivíduo desse grupo tenha uma idade superior a 50 anos.
3. \(P(\sum x \geq 1,600) =\)cdf normal\((1600,E99,1514.10,63) = 0.0864\)
4. \(P(\sum x \leq 1,595) =\)cdf normal\((-E99,1595,1514.10,63) = 0.9005\). Isso significa que há 90% de chance de que a soma das idades do grupo amostral\(n = 49\) seja de no máximo 1595.
5. O 95º percentil = InvNorm\((0.95,30.9,1.1) = 32.7\). Isso indica que 95% das prostitutas da amostra de 65 têm menos de 32,7 anos, em média.
6. O 90º percentil = InvNorm\((0.90,2008.5,72.56) = 2101.5\). Isso indica que 90% das prostitutas da amostra de 65 têm uma soma de idades inferiores a 2.101,5 anos.

Exercício\(\PageIndex{4}\)

De acordo com dados da Boeing, o avião 757 transporta 200 passageiros e tem portas com uma altura média de 72 polegadas. Suponha que, para uma determinada população de homens, tenhamos uma média de 69,0 polegadas e um desvio padrão de 2,8 polegadas.

1. O que a altura média da porta permitiria que 95% dos homens entrassem na aeronave sem se curvar?
2. Suponha que metade dos 200 passageiros sejam homens. Qual altura média da porta satisfaz a condição de que há uma probabilidade de 0,95 de que essa altura seja maior do que a altura média de 100 homens?
3. Para engenheiros que projetam o 757, qual resultado é mais relevante: a altura da parte a ou da parte b? Por quê?

Resposta

1. Sabemos disso\(\mu_{x} = \mu = 69\) e temos\(\sigma_{x} = 2.8\). Verificou-se que a altura da porta é InvNorm\((0.95,69,2.8) = 73.61\)
2. Sabemos disso\(\mu_{x} = \mu = 69\) e temos\(\sigma_{x} = 2.8\). Então, InvNorm\((0.95,69,0.28) = 69.49\)
3. Ao projetar as alturas das portas, precisamos incorporar o máximo de variabilidade possível para acomodar o maior número possível de passageiros. Portanto, precisamos usar o resultado com base na parte a.

Nota histórica: Aproximação normal ao binômio

Historicamente, ser capaz de calcular probabilidades binomiais era uma das aplicações mais importantes do teorema do limite central. Probabilidades binomiais com um valor pequeno para\(n\) (digamos, 20) foram exibidas em uma tabela em um livro. Para calcular as probabilidades com grandes valores de\(n\), era preciso usar a fórmula binomial, o que poderia ser muito complicado. Usar a aproximação normal da distribuição binomial simplificou o processo. Para calcular a aproximação normal da distribuição binomial, pegue uma amostra aleatória simples de uma população. Você deve atender às condições para uma distribuição binomial:

• há um certo número\(n\) de ensaios independentes
• os resultados de qualquer teste são sucesso ou fracasso
• cada tentativa tem a mesma probabilidade de sucesso\(p\)

Lembre-se de que se\(X\) é a variável aleatória binomial, então\(X \sim B(n, p)\). A forma da distribuição binomial precisa ser semelhante à forma da distribuição normal. Para garantir isso, as quantidades\(np\) e ambas\(nq\) devem ser maiores que cinco (\(np > 5\)e\(nq > 5\)); a aproximação é melhor se ambas forem maiores ou iguais a 10). Então, o binômio pode ser aproximado pela distribuição normal com média\(\mu = np\) e desvio padrão\(\sigma = \sqrt{npq}\). Lembre-se disso\(q = 1 - p\). Para obter a melhor aproximação, adicione 0,5\(x\) ou subtraia 0,5 de\(x\) (use\(x + 0.5\) ou\(x - 0.5\)). O número 0,5 é chamado de fator de correção de continuidade e é usado no exemplo a seguir.

Exemplo\(\PageIndex{5}\)

Suponha que em um distrito escolar local do jardim de infância até a ^12ª série (K - 12), 53% da população prefira uma escola charter para as séries K a 5. Uma amostra aleatória simples de 300 é pesquisada.

1. Encontre a probabilidade de que pelo menos 150 favoreçam uma escola charter.
2. Descubra a probabilidade de que no máximo 160 favoreçam uma escola charter.
3. Descubra a probabilidade de que mais de 155 favoreçam uma escola charter.
4. Descubra a probabilidade de que menos de 147 favoreçam uma escola charter.
5. Encontre a probabilidade de que exatamente 175 favoreçam uma escola charter.

Deixe\(X =\) o número que favorece uma escola charter para as séries K a 5. \(X \sim B(n, p)\)onde\(n = 300\)\(p = 0.53\) e. Desde\(np > 5\) e\(nq > 5\), use a aproximação normal do binômio. As fórmulas para a média e o desvio padrão são\(\mu = np\)\(\sigma = \sqrt{npq}\) e. A média é 159 e o desvio padrão é 8,6447. A variável aleatória para a distribuição normal é\(X\). \(Y \sim N(159, 8.6447)\). Consulte A distribuição normal para obter ajuda com as instruções da calculadora.

Para a parte a, você inclui 150, então\(P(X \geq 150)\) a aproximação é normal\(P(Y \geq 149.5) = 0.8641\).

cdf normal\((149.5,10^{99},159,8.6447) = 0.8641\).

Para a parte b, você inclui 160, então\(P(X \leq 160)\) tem uma aproximação normal\(P(Y \leq 160.5) = 0.5689\).

cdf normal\((0,160.5,159,8.6447) = 0.5689\)

Para a parte c, você exclui 155, então\(P(X > 155)\) a aproximação é normal\(P(y > 155.5) = 0.6572\).

cdf normal\((155.5,10^{99},159,8.6447) = 0.6572\).

Para a parte d, você exclui 147, então\(P(X < 147)\) tem aproximação normal\(P(Y < 146.5) = 0.0741\).

cdf normal\((0,146.5,159,8.6447) = 0.0741\)

Para a parte e,\(P(X = 175)\) tem aproximação normal\(P(174.5 < Y < 175.5) = 0.0083\).

cdf normal\((174.5,175.5,159,8.6447) = 0.0083\)

Por causa de calculadoras e softwares de computador que permitem calcular probabilidades binomiais para grandes valores de\(n\) facilmente, não é necessário usar a aproximação normal da distribuição binomial, desde que você tenha acesso a essas ferramentas de tecnologia. A maioria dos laboratórios escolares tem o Microsoft Excel, um exemplo de software de computador que calcula probabilidades binomiais. Muitos estudantes têm acesso às calculadoras da série TI-83 ou 84 e calculam facilmente as probabilidades da distribuição binomial. Se você digitar “cálculo de distribuição de probabilidade binomial” em um navegador da Internet, poderá encontrar pelo menos uma calculadora on-line para o binômio.

Por exemplo, as probabilidades são calculadas usando a seguinte distribuição binomial: (\(n = 300 and p = 0.53\)). Compare as respostas da distribuição binomial e normal. Consulte Variáveis aleatórias discretas para obter ajuda com as instruções da calculadora para o binômio.

\(P(X \geq 150)\): 1 - binômio cdf\((300,0.53,149) = 0.8641\)

\(P(X \leq 160)\): binomial cdf\((300,0.53,160) = 0.5684\)

\(P(X > 155)\): 1 - binômio cdf\((300,0.53,155) = 0.6576\)

\(P(X < 147)\): binomial cdf\((300,0.53,146) = 0.0742\)

\(P(X = 175)\):( Você usa o binômio pdf.) binomial pdf\((300,0.53,175) = 0.0083\)

Exercício\(\PageIndex{5}\)

Em uma cidade, 46% da população favorece a incumbente, Dawn Morgan, para prefeita. Uma amostra aleatória simples de 500 é coletada. Usando o fator de correção de continuidade, encontre a probabilidade de que pelo menos 250 favoreçam Dawn Morgan para prefeita.

Resposta

0,0401

Referências

• Dados do Wall Street Journal.
• “Pesquisa Nacional de Exames de Saúde e Nutrição”. Centro de Controle e Prevenção de Doenças. Disponível on-line em http://www.cdc.gov/nchs/nhanes.htm (acessado em 17 de maio de 2013).

Glossário

Distribuição exponencial

uma variável aleatória contínua (VR) que aparece quando estamos interessados nos intervalos de tempo entre alguns eventos aleatórios, por exemplo, o período de tempo entre as chegadas de emergência em um hospital, notação:\(X \sim Exp(m)\). A média é\(\mu = \dfrac{1}{m}\) e o desvio padrão é\(\sigma = \dfrac{1}{m}\). A função de densidade de probabilidade é\(f(x) = me^{-mx}\),\(x \geq 0\) e a função de distribuição cumulativa é\(P(X \leq x) = 1 - e^{-mx}\).

Significa

um número que mede a tendência central; um nome comum para média é “média”. O termo “média” é uma forma abreviada de “média aritmética”. Por definição, a média de uma amostra (indicada por\(\bar{x}\)) é\(\bar{x} = \dfrac{\text{Sum of all values in the sample}}{\text{Number of values in the sample}}\), e a média de uma população (indicada por\(\mu\)) é\(\mu = \dfrac{\text{Sum of all values in the population}}{\text{Number of values in the population}}\).

Distribuição normal

uma variável aleatória contínua (RV) com pdf\(f(x) = \dfrac{1}{\sigma \sqrt{2\pi}}e^{\dfrac{(x - \mu)^{2}}{2\sigma^{2}}}\), onde\(\mu\) é a média da distribuição e\(\sigma\) é o desvio padrão.; notação:\(X \sim N(\mu, \sigma)\). Se\(\mu = 0\) e\(\sigma = 1\), o RV é chamado de distribuição normal padrão.

Distribuição uniforme

uma variável aleatória contínua (RV) que tem resultados igualmente prováveis sobre o domínio,\(a < x < b\); frequentemente chamada de distribuição retangular porque o gráfico do pdf tem a forma de um retângulo. Notação:\(X \sim U(a, b)\). A média é\(\mu = \dfrac{a+b}{2}\) e o desvio padrão é\(\sigma = \sqrt{\dfrac{(b-a)^{2}}{12}}\). A função de densidade de probabilidade é\(f(x) = \dfrac{a+b}{2}\) para\(a < x < b\) ou\(a \leq x \leq b\). A distribuição cumulativa é\(P(X \leq x) = \dfrac{x-a}{b-a}\).