5.3: A distribuição uniforme

A distribuição uniforme é uma distribuição contínua de probabilidade e está relacionada a eventos que têm a mesma probabilidade de ocorrer. Ao resolver problemas que tenham uma distribuição uniforme, tenha cuidado ao observar se os dados são inclusivos ou exclusivos.

Exemplo 5.3.1

Os dados na Tabela\(\PageIndex{1}\) são 55 vezes sorridentes, em segundos, de um bebê de oito semanas.

Tabela\(\PageIndex{1}\)

10.4	19,6	18,8	13,9	17,8	16,8	21.6	17,9	12,5	11.1	4.9
12,8	14,8	22,8	20,0	15,9	16.3	13,4	17.1	14,5	19,0	22,8
1.3	0.7	8.9	11,9	10.9	7.3	5.9	3.7	17,9	19.2	9.8
5.8	6.9	2.6	5.8	21.7	11,8	3.4	2.1	4.5	6.3	10,7
8.9	9.4	9.4	7.6	10,0	3.3	6.7	7.8	11.6	13,8	18.6

A média da amostra = 11,49 e o desvio padrão da amostra = 6,23.

Assumiremos que os tempos de sorriso, em segundos, seguem uma distribuição uniforme entre zero e 23 segundos, inclusive. Isso significa que qualquer tempo de sorriso de zero a 23 segundos, inclusive, é igualmente provável. O histograma que pode ser construído a partir da amostra é uma distribuição empírica que se aproxima da distribuição uniforme teórica.

Deixe a\(X =\) extensão, em segundos, do sorriso de um bebê de oito semanas.

A notação para a distribuição uniforme é

\(X \sim U(a, b)\)onde\(a =\) o menor valor de\(x\) e\(b =\) o maior valor de\(x\).

A função de densidade de probabilidade é\(f(x) = \frac{1}{b-a}\) para\(a \leq x \leq b\).

Para este exemplo,\(X \sim U(0, 23)\) e\(f(x) = \frac{1}{23-0}\) para\(0 \leq X \leq 23\).

As fórmulas para a média teórica e o desvio padrão são

\[\mu = \frac{a+b}{2} \nonumber\]

e

\[\sigma = \sqrt{\frac{(b-a)^{2}}{12}} \nonumber\]

Para esse problema, a média teórica e o desvio padrão são

\[\mu = \frac{0+23}{2} = 11.50 \, seconds \nonumber\]

e

\[\sigma = \frac{(23-0)^{2}}{12} = 6.64\, seconds. \nonumber\]

Observe que a média teórica e o desvio padrão estão próximos da média e do desvio padrão da amostra neste exemplo.

Exercício\(\PageIndex{1}\)

Os dados a seguir são o número de passageiros em 35 barcos de pesca fretados diferentes. A média da amostra = 7,9 e o desvio padrão da amostra = 4,33. Os dados seguem uma distribuição uniforme em que todos os valores entre zero e 14, incluindo, são igualmente prováveis. Indique os valores de a\(b\) e. Escreva a distribuição na notação correta e calcule a média teórica e o desvio padrão.

Tabela\(\PageIndex{2}\)

1	12	4	10	4	14	11
7	11	4	13	2	4	6
3	10	0	12	6	9	10
5	13	4	10	14	12	11
6	10	11	0	11	13	2

Responda

\(a\)é zero;\(b\) é\(14\);\(X \sim U (0, 14)\);\(\mu = 7\) passageiros;\(\sigma = 4.04\) passageiros

Exemplo 5.3.2A

a. Consulte o Exemplo 5.3.1. Qual é a probabilidade de um bebê de oito semanas escolhido aleatoriamente sorrir entre dois e 18 segundos?

Responda

a. Encontre\(P(2 < x < 18)\).

\(P(2 < x < 18) = (\text{base})(\text{height}) = (18 – 2)\left(\frac{1}{23}\right) = \left(\frac{16}{23}\right)\).

Figura\(\PageIndex{1}\)

Exercício\(\PageIndex{2}\)B

^{b. Encontre o percentil 90 para o tempo de sorriso de um bebê de oito semanas.}

Responda

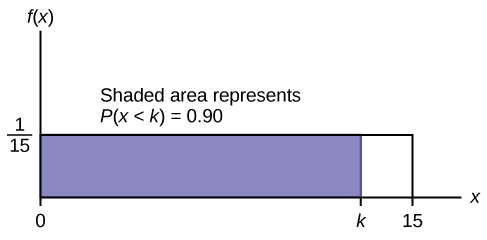
b. Noventa por cento dos tempos de sorriso caem abaixo ^do percentil 90\(k\), então\(P(x < k) = 0.90\)

\[P(x < k)= 0.90\]

\[(\text{base})(\text{height}) = 0.90\]

\[(k−0)\left(\frac{1}{23}\right) = 0.90\]

\[k = (23)(0.90) = 20.7\]

Figura\(\PageIndex{2}\)

Exercício\(\PageIndex{3}\)C

c. Encontre a probabilidade de um bebê aleatório de oito semanas sorrir por mais de 12 segundos SABENDO que o bebê sorri MAIS DE OITO SEGUNDOS.

Responda

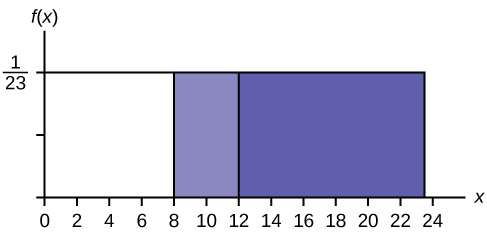
c. Essa questão de probabilidade é condicional. Você deve descobrir a probabilidade de um bebê de oito semanas sorrir por mais de 12 segundos quando você já sabe que o bebê sorriu por mais de oito segundos.

Encontre\(P(x > 12 | x > 8)\) Existem duas maneiras de resolver o problema. Para a primeira maneira, use o fato de que isso é condicional e altera o espaço amostral. O gráfico ilustra o novo espaço amostral. Você já sabe que o bebê sorriu por mais de oito segundos.

Escreva um novo\(f(x): f(x) = \frac{1}{23-8} = \frac{1}{15}\)

para\(8 < x < 23\)

\(P(x > 12 | x > 8) = (23 − 12)\left(\frac{1}{15}\right) = \left(\frac{11}{15}\right)\)

Figura\(\PageIndex{3}\)

Para a segunda forma, use a fórmula condicional dos Tópicos de Probabilidade com a distribuição original\(X \sim U(0, 23)\):

\(P(\text{A|B}) = \frac{P(\text{A AND B})}{P(\text{B})}\)

Para esse problema,\(\text{A}\) is (\(x > 12\)) e\(\text{B}\) is (\(x > 8\)).

Então,\(P(x > 12|x > 8) = \frac{(x > 12 \text{ AND } x > 8)}{P(x > 8)} = \frac{P(x > 12)}{P(x > 8)} = \frac{\frac{11}{23}}{\frac{15}{23}} = \frac{11}{15}\)

Figura\(\PageIndex{4}\): A área sombreada mais escura representa\(P(x > 12)\). Toda a área sombreada é exibida\(P(x > 8)\).

Exercício\(\PageIndex{2}\)

Uma distribuição é dada como\(X \sim U(0, 20)\). O que é\(P(2 < x < 18)\)? Encontre o ^90º percentil.

Responda

\(P(2 < x < 18) = 0.8\); 90 ^º percentil\(= 18\)

Exemplo 5.3.3

A quantidade de tempo, em minutos, que uma pessoa deve esperar por um ônibus é distribuída uniformemente entre zero e 15 minutos, inclusive.

Exercício\(\PageIndex{3}\).1

a. Qual é a probabilidade de uma pessoa esperar menos de 12,5 minutos?

Responda

a. Deixe\(X =\) o número de minutos que uma pessoa deve esperar por um ônibus. \(a = 0\)\(b = 15\)e. \(X \sim U(0, 15)\). Escreva a função de densidade de probabilidade. \(f(x) = \frac{1}{15-0} = \frac{1}{15}\)para\(0 \leq x \leq 15\).

Encontre\(P(x < 12.5)\). Desenhe um gráfico.

\[P(x < k) = (\text{base})(\text{height}) = (12.5−0)\left(\frac{1}{15}\right) = 0.8333\]

A probabilidade de uma pessoa esperar menos de 12,5 minutos é de 0,8333.

Figura\(\PageIndex{5}\).

Exercício\(\PageIndex{3}\).2

b. Em média, quanto tempo uma pessoa deve esperar? Encontre a média\(\mu\), e o desvio padrão,\(\sigma\).

Responda

\(\mu = \frac{a+b}{2} = \frac{15+0}{2} = 7.5\)b. Em média, uma pessoa deve esperar 7,5 minutos.

\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}} = \sqrt{\frac{(12-0)^{2}}{12}} = 4.3\). O desvio padrão é de 4,3 minutos.

Exercício\(\PageIndex{3}\).3

c. Noventa por cento das vezes, o tempo que uma pessoa deve esperar cai abaixo de qual valor?

Nota 5.3.3.3.1

^{Isso pede o percentil 90.}

Responda

c. Encontre o ^90º percentil. Desenhe um gráfico. Deixe\(k =\) o ^90º percentil.

\(P(x < k) = (\text{base})(\text{height}) = (k−0)\left(\frac{1}{15}\right)\)
\(0.90 = (k)\left(\frac{1}{15}\right)\)
\(k = (0.90)(15) = 13.5\)
\(k\)às vezes é chamado de valor crítico.
^{O percentil 90 é de 13,5 minutos.} Noventa por cento das vezes, uma pessoa deve esperar no máximo 13,5 minutos.

Figura\(\PageIndex{6}\).

Exercício\(\PageIndex{4}\)

A duração total dos jogos de beisebol na liga principal na temporada de 2011 é distribuída uniformemente entre 447 horas e 521 horas, inclusive.

1. Encontre\(a\)\(b\) e descreva o que eles representam.
2. Escreva a distribuição.
3. Encontre a média e o desvio padrão.
4. Qual é a probabilidade de que a duração dos jogos de uma equipe na temporada de 2011 seja entre 480 e 500 horas?
5. ^{Qual é o percentil 65 para a duração dos jogos de uma equipe na temporada de 2011?}

Responda

1. \(a\)é\(447\) e\(b\) é\(521\). a é a duração mínima dos jogos de uma equipe na temporada de 2011 e\(b\) é a duração máxima dos jogos de uma equipe na temporada de 2011.
2. \(X \sim U(447, 521)\).
3. \(\mu = 484\), e\(\sigma = 21.36\)

   

   Figura\(\PageIndex{1}\).

4. \(P(480 < x < 500) = 0.2703\)
5. ^O percentil 65 é 495,1 horas.

Exemplo 5.3.4

Suponha que o tempo que uma criança de nove anos leve para comer um donut seja entre 0,5 e 4 minutos, inclusive. Deixe\(X =\) o tempo, em minutos, que uma criança de nove anos leve para comer uma rosquinha. Então\(X \sim U(0.5, 4)\).

a. A probabilidade de uma criança de nove anos selecionada aleatoriamente comer uma rosquinha em pelo menos dois minutos é _______.

Solução

a. 0,5714

Exercício\(\PageIndex{4}\).1

b. Encontre a probabilidade de uma criança diferente de nove anos comer uma rosquinha em mais de dois minutos, já que a criança já está comendo a rosquinha há mais de 1,5 minutos.

A segunda pergunta tem uma probabilidade condicional. Você deve descobrir a probabilidade de uma criança de nove anos comer uma rosquinha em mais de dois minutos, já que a criança já está comendo a rosquinha há mais de 1,5 minutos. Resolva o problema de duas maneiras diferentes (veja o exemplo). Você deve reduzir o espaço da amostra. Primeira maneira: como você sabe que a criança já está comendo a rosquinha há mais de 1,5 minutos, você não está mais começando com a = 0,5 minutos. Seu ponto de partida é de 1,5 minutos.

Escreva um novo\(f(x)\):

\(f(x) = \frac{1}{4-1.5} = \frac{2}{5}\)para\(1.5 \leq x \leq 4\).

Encontre\(P(x > 2|x > 1.5)\). Desenhe um gráfico.

Figura\(\PageIndex{2}\).

\(P(x > 2|x > 1.5) = (\text{base})(\text{new height}) = (4 − 2)(25)\left(\frac{2}{5}\right) =\)?

Responda

b.\(\frac{4}{5}\)

A probabilidade de uma criança de nove anos comer uma rosquinha em mais de dois minutos, já que a criança já está comendo a rosquinha há mais de 1,5 minutos, é\(\frac{4}{5}\).

Segunda maneira: desenhe o gráfico original para\(X \sim U(0.5, 4)\). Use a fórmula condicional

\(P(x > 2 | x > 1.5) = \frac{P(x > 2 \text{AND} x > 1.5)}{P(x > 1.5)} = \frac{P(x>2)}{P(x>1.5)} = \frac{\frac{2}{3.5}}{\frac{2.5}{3.5}} = 0.8 = \frac{4}{5}\)

Exercício\(\PageIndex{5}\)

Suponha que o tempo que um aluno leva para concluir um questionário seja distribuído uniformemente entre seis e 15 minutos, inclusive. Deixe\(X =\) o tempo, em minutos, que o aluno leva para terminar um questionário. Então\(X \sim U(6, 15)\).

Encontre a probabilidade de um aluno selecionado aleatoriamente precisar de pelo menos oito minutos para concluir o questionário. Em seguida, encontre a probabilidade de que um aluno diferente precise de pelo menos oito minutos para terminar o questionário, já que ela já fez mais de sete minutos.

Responda

\(P(x > 8) = 0.7778\)

\(P(x > 8 | x > 7) = 0.875\)

Exemplo 5.3.5

O Ace Heating and Air Conditioning Service descobriu que a quantidade de tempo que um técnico precisa para consertar um forno é distribuída uniformemente entre 1,5 e quatro horas. Reserve\(x =\) o tempo necessário para consertar um forno. Então\(x \sim U(1.5, 4)\).

1. Encontre a probabilidade de que um reparo de forno selecionado aleatoriamente exija mais de duas horas.
2. Determine a probabilidade de que um reparo de forno selecionado aleatoriamente exija menos de três horas.
3. Encontre o ^30º percentil dos tempos de reparo do forno.
4. Os 25% mais longos dos tempos de reparo do forno demoram pelo menos quanto tempo? (Em outras palavras: encontre o tempo mínimo para os 25% mais longos dos tempos de reparo.) Que percentil isso representa?
5. Encontre a média e o desvio padrão

Solução

a. Para descobrir\(f(x): f(x) = \frac{1}{4-1.5} = \frac{1}{2.5}\) isso\(f(x) = 0.4\)

\(P(x > 2) = (\text{base})(\text{height}) = (4 – 2)(0.4) = 0.8\)

Figura\(\PageIndex{3}\). Distribuição uniforme entre 1,5 e quatro com área sombreada entre dois e quatro representando a probabilidade de que o tempo de reparo\(x\) seja maior que dois

b.\(P(x < 3) = (\text{base})(\text{height}) = (3 – 1.5)(0.4) = 0.6\)

O gráfico do retângulo mostrando toda a distribuição permaneceria o mesmo. No entanto, o gráfico deve estar sombreado entre\(x = 1.5\)\(x = 3\) e. Observe que a área sombreada começa em\(x = 1.5\) vez de em\(x = 0\); desde então\(X \sim U(1.5, 4)\), não\(x\) pode ser menor que 1,5.

Figura\(\PageIndex{4}\). Distribuição uniforme entre 1,5 e quatro com área sombreada entre 1,5 e três representando a probabilidade de que o tempo de reparo\(x\) seja menor que três

c.

Figura\(\PageIndex{5}\). Distribuição uniforme entre 1,5 e 4 com uma área de 0,30 sombreada à esquerda, representando os menores 30% dos tempos de reparo.

\(P(x < k) = 0.30\)
\(P(x < k) = (\text{base})(\text{height}) = (k – 1.5)(0.4)\)
\(0.3 = (k – 1.5) (0.4)\); Resolva para encontrar\(k\):
\(0.75 = k – 1.5\), obtido dividindo os dois lados por 0,4
\(k = 2.25\), obtido adicionando 1,5 aos dois lados

^{O percentil 30 dos tempos de reparo é de 2,25 horas. 30% dos tempos de reparo são 2,25 horas ou menos.}

d.

Figura\(\PageIndex{6}\). Distribuição uniforme entre 1,5 e 4 com uma área de 0,25 sombreada à direita, representando os 25% mais longos dos tempos de reparo.

\(P(x > k) = 0.25\)
\(P(x > k) = (\text{base})(\text{height}) = (4 – k)(0.4)\)
\(0.25 = (4 – k)(0.4)\); Resolva para\(k\):
\(0.625 = 4 − k\),
obtido dividindo os dois lados por 0,4
\(−3.375 = −k\),
obtido subtraindo quatro de ambos os lados: \(k = 3.375\)
Os 25% mais longos dos reparos no forno levam pelo menos 3.375 horas (3.375 horas ou mais).

Nota: Como 25% dos tempos de reparo são de 3.375 horas ou mais, isso significa que 75% dos tempos de reparo são 3.375 horas ou menos. 3.375 horas é o ^75º percentil dos tempos de reparo do forno.

e.\(\mu = \frac{a+b}{2}\) e\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\)

\(\mu = \frac{1.5+4}{2} = 2.75\)horas e\(\sigma = \sqrt{\frac{(4-1.5)^{2}}{12}} = 0.7217\) horas

Exercício\(\PageIndex{6}\)

A quantidade de tempo que um técnico de manutenção precisa para trocar o óleo de um carro é distribuída uniformemente entre 11 e 21 minutos. Reserve\(X =\) o tempo necessário para trocar o óleo de um carro.

1. Escreva a variável aleatória\(X\) em palavras. \(X =\)__________________.
2. Escreva a distribuição.
3. Faça um gráfico da distribuição.
4. Encontre\(P(x > 19)\).
5. ^{Encontre o percentil 50.}

Responda

1. Reserve\(X =\) o tempo necessário para trocar o óleo em um carro.
2. \(X \sim U(11, 21)\).

3. 

   Figura\(\PageIndex{7}\).

4. \(P(x > 19) = 0.2\)
5. ^{o percentil 50 é de 16 minutos.}

Revisão

Se\(X\) tem uma distribuição uniforme onde\(a < x < b\) ou\(a \leq x \leq b\), então\(X\) assume valores entre\(a\) e\(b\) (pode incluir\(a\) e\(b\)). Todos os valores\(x\) são igualmente prováveis. Nós escrevemos\(X \sim U(a, b)\). A média de\(X\) é\(\mu = \frac{a+b}{2}\). O desvio padrão de\(X\) é\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\). A função de densidade de probabilidade de\(X\) é\(f(x) = \frac{1}{b-a}\) para\(a \leq x \leq b\). A função de distribuição cumulativa de\(X\) é\(P(X \leq x) = \frac{x-a}{b-a}\). \(X\)é contínuo.

Figura\(\PageIndex{8}\).

A probabilidade\(P(c < X < d)\) pode ser encontrada computando a área abaixo\(f(x)\), entre\(c\)\(d\) e. Como a área correspondente é um retângulo, a área pode ser encontrada simplesmente multiplicando a largura e a altura.

Revisão da fórmula

\(X =\)um número real entre\(a\) e\(b\) (em alguns casos,\(X\) pode assumir os valores\(a\) e\(b\)). \(a =\)menor\(X\);\(b =\) maior\(X\)

\(X \sim U(a, b)\)

A média é\(\mu = \frac{a+b}{2}\)

O desvio padrão é\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\)

Função de densidade de probabilidade:\(f(x) = \frac{1}{b-a} \text{for} a \leq X \leq b\)

Área à esquerda de\(x\):\(P(X < x) = (x – a)\left(\frac{1}{b-a}\right)\)

Área à direita de\(x\): P (\(X\)>\(x\)) = (b — x)\(\left(\frac{1}{b-a}\right)\)

Área entre\(c\) e\(d\):\(P(c < x < d) = (\text{base})(\text{height}) = (d – c)\left(\frac{1}{b-a}\right)\)

Uniforme:\(X \sim U(a, b)\) onde\(a < x < b\)

• pdf:\(f(x) = \frac{1}{b-a}\) para\(a \leq x \leq b\)
• cdf:\(P(X \leq x) = \frac{x-a}{b-a}\)
• quero dizer\(\mu = \frac{a+b}{2}\)
• desvio padrão\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\)
• \(P(c < X < d) = (d – c)\left(\frac{1}{b-a}\right)\)

Referências

McDougall, John A. O Programa McDougall para perda máxima de peso. Plume, 1995.

Use as informações a seguir para responder às próximas dez perguntas. Os dados a seguir são a metragem quadrada (em 1.000 pés quadrados) de 28 casas.

1,5	2.4	3.6	2.6	1.6	2.4	2.0
3.5	2,5	1.8	2.4	2,5	3.5	4.0
2.6	1.6	2.2	1.8	3.8	2,5	1,5
2.8	1.8	4.5	1.9	1.9	3.1	1.6

A média da amostra = 2,50 e o desvio padrão da amostra = 0,8302.

A distribuição pode ser escrita como\(X \sim U(1.5, 4.5)\).

Exercício\(\PageIndex{7}\)

Que tipo de distribuição é essa?

Exercício\(\PageIndex{8}\)

Nessa distribuição, os resultados são igualmente prováveis. O que isso significa?

Responda

Isso significa que o valor de x tem a mesma probabilidade de ser qualquer número entre 1,5 e 4,5.

Exercício\(\PageIndex{9}\)

Qual é a altura de\(f(x)\) para a distribuição contínua de probabilidade?

Exercício\(\PageIndex{10}\)

Quais são as restrições para os valores de\(x\)?

Responda

\(1.5 \leq x \leq 4.5\)

Exercício\(\PageIndex{11}\)

Gráfico\(P(2 < x < 3)\).

Exercício\(\PageIndex{12}\)

O que é\(P(2 < x < 3)\)?

Responda

0,333

Exercício\(\PageIndex{13}\)

O que é\(P(x < 3.5 | x < 4)\)?

Exercício\(\PageIndex{14}\)

O que é\(P(x = 1.5)\)?

Responda

zero

Exercício\(\PageIndex{15}\)

^{Qual é o percentil 90 da metragem quadrada para residências?}

Exercício\(\PageIndex{16}\)

Encontre a probabilidade de uma casa selecionada aleatoriamente ter mais de 3.000 pés quadrados, já que você já sabe que a casa tem mais de 2.000 pés quadrados.

Responda

0,6

Exercício\(\PageIndex{17}\)

O que é\(a\)? O que isso representa?

Exercício\(\PageIndex{18}\)

O que é\(b\)? O que isso representa?

Responda

\(b\)é\(12\), e representa o maior valor de\(x\).

Exercício\(\PageIndex{19}\)

O que é a função de densidade de probabilidade?

Exercício\(\PageIndex{20}\)

Qual é a média teórica?

Responda

seis

Exercício\(\PageIndex{21}\)

Qual é o desvio padrão teórico?

Exercício\(\PageIndex{22}\)

Desenhe o gráfico da distribuição para\(P(x > 9)\).

Responda

Figura\(\PageIndex{9}\).

Exercício\(\PageIndex{23}\)

Encontre\(P(x > 9)\).

Exercício\(\PageIndex{24}\)

Encontre o ^40º percentil.

Responda

4.8

Use as informações a seguir para responder aos próximos onze exercícios. A idade dos carros no estacionamento dos funcionários de uma faculdade suburbana é distribuída uniformemente de seis meses (0,5 anos) a 9,5 anos.

Exercício\(\PageIndex{25}\)

O que está sendo medido aqui?

Exercício\(\PageIndex{26}\)

Em palavras, defina a variável aleatória\(X\).

Responda

\(X\)= A idade (em anos) dos carros no estacionamento dos funcionários

Exercício\(\PageIndex{27}\)

Os dados são discretos ou contínuos?

Exercício\(\PageIndex{28}\)

O intervalo de valores para\(x\) é ______.

Responda

0,5 a 9,5

Exercício\(\PageIndex{29}\)

A distribuição para\(X\) é ______.

Exercício\(\PageIndex{30}\)

Escreva a função de densidade de probabilidade.

Responda

\(f(x) = \frac{1}{9}\)onde\(x\) está entre 0,5 e 9,5, inclusive.

Exercício\(\PageIndex{31}\)

Faça um gráfico da distribuição de probabilidade.

1. Esboce o gráfico da distribuição de probabilidade.

   

   Figura\(\PageIndex{10}\).

2. Identifique os seguintes valores:
   1. Valor mais baixo para\(\bar{x}\): _______
   2. Valor mais alto para\(\bar{x}\): _______
   3. Altura do retângulo: _______
   4. Rótulo para o eixo x (palavras): _______
   5. Rótulo para o eixo y (palavras): _______

Exercício\(\PageIndex{32}\)

Encontre a idade média dos carros no estacionamento.

Responda

\(\mu\)= 5

Exercício\(\PageIndex{33}\)

Encontre a probabilidade de um carro escolhido aleatoriamente no estacionamento ter menos de quatro anos.

1. Desenhe o gráfico e sombreie a área de interesse.

   

   Figura\(\PageIndex{11}\).

2. Encontre a probabilidade. \(P(x < 4) =\)_______

Exercício\(\PageIndex{34}\)

Considerando apenas os carros com menos de 7,5 anos, determine a probabilidade de que um carro escolhido aleatoriamente no estacionamento tenha menos de quatro anos.

1. Desenhe o gráfico, sombreie a área de interesse.

   

   Figura\(\PageIndex{12}\).

2. Encontre a probabilidade. \(P(x < 4 | x < 7.5) =\)_______

Responda

1. Verifique a solução do aluno.
2. \(\frac{3.5}{7}\)

Exercício\(\PageIndex{35}\)

O que mudou nos dois problemas anteriores que tornaram as soluções diferentes

Exercício\(\PageIndex{36}\)

Encontre o terceiro quartil de idades dos carros no lote. Isso significa que você terá que encontrar o valor de tal forma que\(\frac{3}{4}\), ou 75%, dos carros tenham no máximo (menor ou igual a) essa idade.

1. Desenhe o gráfico e sombreie a área de interesse.

   

   Figura\(\PageIndex{13}\).

2. Encontre o valor de\(k\) tal forma que\(P(x < k) = 0.75\).
3. O terceiro quartil é _______

Resposta

1. Verifique a solução do aluno.
2. \(k = 7.25\)
3. \(7.25\)

Glossário

Probabilidade condicional

a probabilidade de que um evento ocorra, uma vez que outro evento já ocorreu