Skip to main content
Global

5.2: Funções de probabilidade contínuas

  1. Last updated
  2. Save as PDF
  • Page ID
    190147

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Começamos definindo uma função de densidade de probabilidade contínua. Usamos a notação da função\(f(x)\). A álgebra intermediária pode ter sido sua primeira introdução formal às funções. No estudo da probabilidade, as funções que estudamos são especiais. Definimos a função\(f(x)\) para que a área entre ela e o eixo x seja igual a uma probabilidade. Como a probabilidade máxima é uma, a área máxima também é uma. Para distribuições de probabilidade contínuas, PROBABILIDADE = ÁREA.

    Exemplo\(\PageIndex{1}\)

    Considere a função\(f(x) = \frac{1}{20}\) para\(0 \leq x \leq 20\). \(x =\)um número real. O gráfico de\(f(x) = \frac{1}{20}\) é uma linha horizontal. No entanto\(0 \leq x \leq 20\), uma vez que,\(f(x)\) está restrito à porção entre\(x = 0\) e\(x = 20\), inclusive.

    Isso mostra o gráfico da função f (x) = 1/20. Uma linha horizontal varia do ponto (0, 1/20) até o ponto (20, 1/20). Uma linha vertical se estende do eixo x até o final da linha no ponto (20, 1/20) criando um retângulo.
    Figura\(\PageIndex{1}\)

    \[f(x) = \frac{1}{20} \text{ for } 0 \leq x \leq 20.\]

    O gráfico de\(f(x) = \frac{1}{20}\) é um segmento de linha horizontal quando\(0 \leq x \leq 20\).

    A área entre\(f(x) = \frac{1}{20}\) onde\(0 \leq x \leq 20\) e o eixo x é a área de um retângulo com base = 20 e altura =\(\frac{1}{20}\).

    \[AREA = 20 \left(\frac{1}{20} \right) = 1\]

    Suponha que queremos encontrar a área entre\(f(x) = \frac{1}{20}\) e o eixo x onde\(0 < x < 2\).

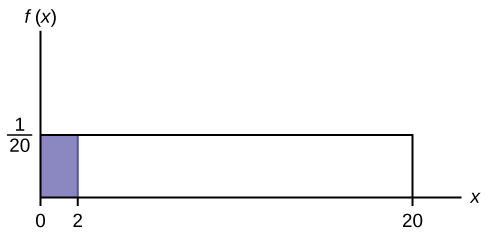
    5.1.2.pngIsso mostra o gráfico da função f (x) = 1/20. Uma linha horizontal varia do ponto (0, 1/20) até o ponto (20, 1/20). Uma linha vertical se estende do eixo x até o final da linha no ponto (20, 1/20) criando um retângulo. Uma região é sombreada dentro do retângulo de x = 0 a x = 2.
    Figura\(\PageIndex{2}\)

    \[AREA = (2 - 0) \left(\dfrac{1}{20} \right) = 0.1\]

    \((2 - 0) = 2 = \text{base of a rectangle}\)

    LEMBRETE: área de um retângulo = (base) (altura).

    A área corresponde a uma probabilidade. A probabilidade de que x esteja entre zero e dois é 0,1, o que pode ser escrito matematicamente como\(P(0 < x < 2) = P(x < 2) = 0.1\).

    Suponha que queremos encontrar a área entre\(f(x) = \frac{1}{20}\) e o eixo x onde\(4 < x < 15\).

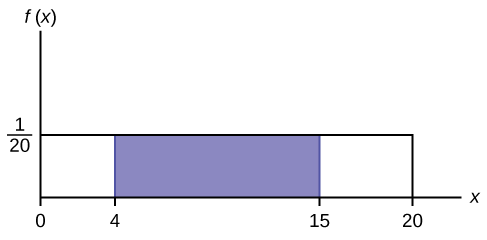
    Isso mostra o gráfico da função f (x) = 1/20. Uma linha horizontal varia do ponto (0, 1/20) até o ponto (20, 1/20). Uma linha vertical se estende do eixo x até o final da linha no ponto (20, 1/20) criando um retângulo. Uma região é sombreada dentro do retângulo de x = 4 a x = 15.
    Figura\(\PageIndex{3}\)

    \(\text{AREA} = (15 – 4)(\frac{1}{20}) = 0.55\)

    \(\text{AREA} = (15 – 4)(\frac{1}{20}) = 0.55\)

    \((15 – 4) = 11 = \text{the base of a rectangle}(15 – 4) = 11 = \text{the base of a rectangle}\)

    A área corresponde à probabilidade\(P(4 < x < 15) = 0.55\).

    Suponha que queiramos encontrar\(P(x = 15)\). Em um gráfico x-y,\(x = 15\) é uma linha vertical. Uma linha vertical não tem largura (ou largura zero). Portanto,\(P(x = 15) = (\text{base})(\text{height}) = (0)\left(\frac{1}{20}\right) = 0\)

    Isso mostra o gráfico da função f (x) = 1/20. Uma linha horizontal varia do ponto (0, 1/20) até o ponto (20, 1/20). Uma linha vertical se estende do eixo x até o final da linha no ponto (20, 1/20) criando um retângulo. Uma linha vertical se estende do eixo horizontal até o gráfico em x = 15.
    Figura\(\PageIndex{4}\)

    \(P(X \leq x)\)(pode ser escrito como\(P(X < x)\) para distribuições contínuas) é chamado de função de distribuição cumulativa ou CDF. Observe o símbolo “menor ou igual a”. Podemos usar o CDF para calcular\(P(X > x)\). O CDF dá “área à esquerda” e\(P(X > x)\) dá “área à direita”. Calculamos\(P(X > x)\) para distribuições contínuas da seguinte forma:\(P(X > x) = 1 – P(X < x)\).

    Isso mostra o gráfico da função f (x) = 1/20. Uma linha horizontal varia do ponto (0, 1/20) até o ponto (20, 1/20). Uma linha vertical se estende do eixo x até o final da linha no ponto (20, 1/20) criando um retângulo. A área à esquerda de um valor, x, está sombreada.
    Figura\(\PageIndex{5}\)

    Identifique o gráfico com\(f(x)\)\(x\) e. Dimensione os\(y\) eixos\(x\) e com o máximo\(x\) e\(y\) os valores. \(f(x) = \frac{1}{20}\),\(0 \leq x \leq 20\).

    Para calcular a probabilidade que\(x\) está entre dois valores, veja o gráfico a seguir. Sombreie a região entre\(x = 2.3\)\(x = 12.7\) e. Em seguida, calcule a área sombreada de um retângulo.

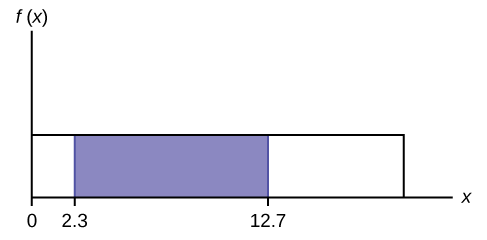
    Isso mostra o gráfico da função f (x) = 1/20. Uma linha horizontal varia do ponto (0, 1/20) até o ponto (20, 1/20). Uma linha vertical se estende do eixo x até o final da linha no ponto (20, 1/20) criando um retângulo. Uma região é sombreada dentro do retângulo de x = 2,3 a x = 12,7
    Figura\(\PageIndex{6}\)

    \[P(2.3 < x < 12.7) = (\text{base})(\text{height}) = (12.7−2.3)\left(\dfrac{1}{20}\right) = 0.52\]

    Exercício\(\PageIndex{1}\)

    Considere a função\(f(x) = \frac{1}{8}\) para\(0 \leq x \leq 8\). Desenhe o gráfico\(f(x)\) e encontre\(P(2.5 < x < 7.5)\).

    Responda
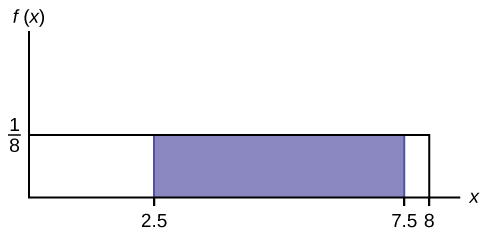
    5.1.7.png
    Figura\(\PageIndex{7}\)

    \(P (2.5 < x < 7.5) = 0.625\)

    Resumo

    A função de densidade de probabilidade (pdf) é usada para descrever probabilidades para variáveis aleatórias contínuas. A área sob a curva de densidade entre dois pontos corresponde à probabilidade de a variável ficar entre esses dois valores. Em outras palavras, a área sob a curva de densidade entre os pontos a e b é igual\(P(a < x < b)\) a. A função de distribuição cumulativa (cdf) fornece a probabilidade como uma área. Se\(X\) for uma variável aleatória contínua, a função de densidade de probabilidade (pdf)\(f(x)\),, é usada para desenhar o gráfico da distribuição de probabilidade. A área total abaixo do gráfico de\(f(x)\) é um. A área abaixo do gráfico\(f(x)\) e entre os valores a e b fornece a probabilidade\(P(a < x < b)\).

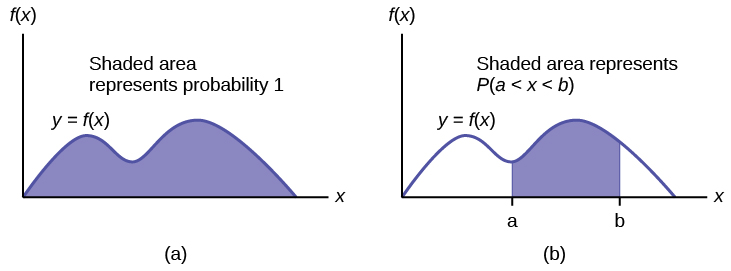
    O gráfico à esquerda mostra uma curva de densidade geral, y = f (x). A região abaixo da curva e acima do eixo x está sombreada. A área da região sombreada é igual a 1. Isso mostra que todos os resultados possíveis são representados pela curva. O gráfico à direita mostra a mesma curva de densidade. As linhas verticais x = a e x = b se estendem do eixo até a curva e a área entre as linhas é sombreada. A área da região sombreada representa a probabilidade y de que um valor x fique entre a e b.
    Figura\(\PageIndex{8}\)

    A função de distribuição cumulativa (cdf) de\(X\) é definida por\(P(X \leq x)\). É uma função\(x\) que dá a probabilidade de que a variável aleatória seja menor ou igual\(x\) a.

    Revisão da fórmula

    Função de densidade de probabilidade (pdf)\(f(x)\):

    • \(f(x) \geq 0\)
    • A área total abaixo da curva\(f(x)\) é uma.

    Função de distribuição cumulativa (cdf):\(P(X \leq x)\)