5.1: Introdução
- Page ID
- 190148
OBJETIVO DO CAPÍTULO
No final deste capítulo, o aluno deverá ser capaz de:
- Reconheça e compreenda as funções de densidade de probabilidade contínua em geral.
- Reconheça a distribuição uniforme de probabilidade e aplique-a adequadamente.
- Reconheça a distribuição de probabilidade exponencial e aplique-a adequadamente.
Variáveis aleatórias contínuas têm muitas aplicações. As médias de rebatidas de beisebol, as pontuações de QI, a duração de uma ligação telefônica de longa distância, a quantidade de dinheiro que uma pessoa carrega, a duração de um chip de computador e os resultados do SAT são apenas alguns. O campo da confiabilidade depende de uma variedade de variáveis aleatórias contínuas.
Os valores das variáveis aleatórias discretas e contínuas podem ser ambíguos. Por exemplo, se\(X\) for igual ao número de milhas (até a milha mais próxima) que você dirige até o trabalho, então\(X\) é uma variável aleatória discreta. Você conta as milhas. Se\(X\) é a distância que você dirige até o trabalho, então você mede os valores de\(X\) e\(X\) é uma variável aleatória contínua. Para um segundo exemplo, se\(X\) for igual ao número de livros em uma mochila, então\(X\) é uma variável aleatória discreta. Se\(X\) é o peso de um livro, então\(X\) é uma variável aleatória contínua porque os pesos são medidos. A forma como a variável aleatória é definida é muito importante.

Propriedades das distribuições contínuas de probabilidade
O gráfico de uma distribuição contínua de probabilidade é uma curva. A probabilidade é representada pela área abaixo da curva. A curva é chamada de função de densidade de probabilidade (abreviada como pdf). Usamos o símbolo\(f(x)\) para representar a curva. \(f(x)\)é a função que corresponde ao gráfico; usamos a função densidade\(f(x)\) para desenhar o gráfico da distribuição de probabilidade. A área abaixo da curva é dada por uma função diferente chamada função de distribuição cumulativa (abreviada como cdf). A função de distribuição cumulativa é usada para avaliar a probabilidade como área.
- Os resultados são medidos, não contados.
- Toda a área abaixo da curva e acima do eixo x é igual a um.
- A probabilidade é encontrada para intervalos de\(x\) valores em vez de\(x\) valores individuais.
- \(P(c < x < d)\)é a probabilidade de que a variável aleatória\(X\) esteja no intervalo entre os valores\(c\)\(d\) e. \(P(c < x < d)\)é a área abaixo da curva, acima do eixo x, à direita\(c\) e à esquerda de\(d\).
- \(P(x = c) = 0\)A probabilidade que\(x\) assume qualquer valor individual é zero. A área abaixo da curva, acima do eixo x e entre\(x = c\) e não\(x = c\) tem largura e, portanto, nenhuma área (área = 0). Como a probabilidade é igual à área, a probabilidade também é zero.
- \(P(c < x < d)\)é o mesmo\(P(c \leq x \leq d)\) porque a probabilidade é igual à área.
Encontraremos a área que representa probabilidade usando geometria, fórmulas, tecnologia ou tabelas de probabilidade. Em geral, o cálculo é necessário para encontrar a área abaixo da curva para muitas funções de densidade de probabilidade. Quando usamos fórmulas para encontrar a área neste livro didático, as fórmulas foram encontradas usando as técnicas de cálculo integral. No entanto, como a maioria dos estudantes deste curso não estudou cálculo, não usaremos cálculo neste livro didático. Há muitas distribuições de probabilidade contínuas. Ao usar uma distribuição de probabilidade contínua para modelar a probabilidade, a distribuição usada é selecionada para modelar e ajustar a situação específica da melhor maneira.
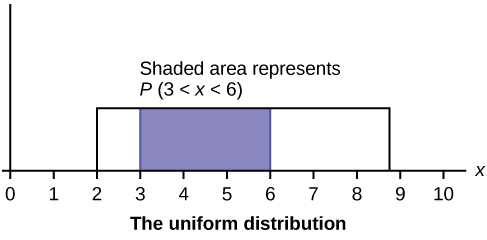
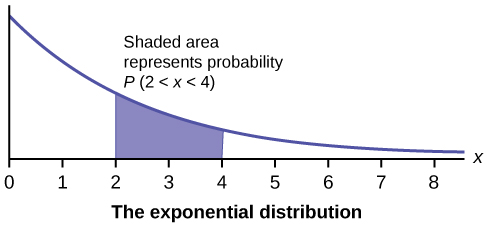
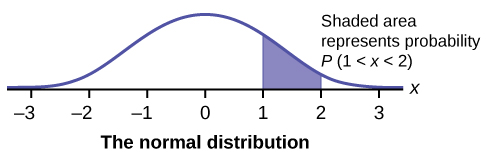
Neste capítulo e no próximo, estudaremos a distribuição uniforme, a distribuição exponencial e a distribuição normal. Os gráficos a seguir ilustram essas distribuições.
Glossário
- Distribuição uniforme
- uma variável aleatória contínua (RV) que tem resultados igualmente prováveis sobre o domínio\(a < x < b\); geralmente é chamada de distribuição retangular porque o gráfico do pdf tem a forma de um retângulo. Notação:\(X \sim U(a,b)\). A média é\(\mu = \frac{a+b}{2}\) e o desvio padrão é\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\). A função de densidade de probabilidade é\(f(x) = \frac{1}{b-a}\) para\(a < x < b\) ou\(a \leq x \leq b\). A distribuição cumulativa é\(P(X \leq x) = \frac{x-a}{b-a}\).
- Distribuição exponencial
- uma variável aleatória contínua (VR) que aparece quando estamos interessados nos intervalos de tempo entre alguns eventos aleatórios, por exemplo, o período de tempo entre as chegadas de emergência em um hospital; a notação é\(X \sim \text{Exp}(m)\). A média é\(\mu = \frac{1}{m}\) e o desvio padrão é\(\sigma = \frac{1}{m}\). A função de densidade de probabilidade é\(f(x) = me^{-mx}\),\(x \geq 0\) e a função de distribuição cumulativa é\(P(X \leq x) = 1 − e^{mx}\).


