Skip to main content
Global

10.5: Representação gráfica de equações quadráticas

  1. Last updated
  2. Save as PDF
  • Page ID
    184104

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Reconheça o gráfico de uma equação quadrática em duas variáveis
    • Encontre o eixo de simetria e o vértice de uma parábola
    • Encontre as interceptações de uma parábola
    • Representar graficamente equações quadráticas em duas variáveis
    • Resolva aplicações máximas e mínimas
    Esteja preparado

    Antes de começar, faça este teste de prontidão.

    1. Faça um gráfico da equação\(y=3x−5\) traçando pontos.
      Se você perdeu esse problema, revise [link].
    2. Avalie\(2x^2+4x−1\) quando\(x=−3\)
      Se você perdeu esse problema, revise [link].
    3. Avalie\(−\frac{b}{2a}\) quando\(a=13\) e b=\(\frac{5}{6}\)
      Se você perdeu esse problema, revise [link].

    Reconhecer o gráfico de uma equação quadrática em duas variáveis

    Representamos graficamente as equações do formulário\(Ax+By=C\). Chamamos equações como essas de equações lineares porque seus gráficos são linhas retas.

    Agora, representaremos graficamente as equações do formulário\(y=ax^2+bx+c\). Chamamos esse tipo de equação de equação quadrática em duas variáveis.

    definição: EQUAÇÃO QUADRÁTICA EM DUAS VARIÁVEIS

    Uma equação quadrática em duas variáveis, onde a, b e c são números reais e\(a\neq 0\), é uma equação da forma\[y=ax^2+bx+c \nonumber\]

    Assim como começamos a representar graficamente equações lineares traçando pontos, faremos o mesmo com equações quadráticas.

    Vejamos primeiro a representação gráfica da equação quadrática\(y=x^2\). Escolheremos valores inteiros de x entre −2 e 2 e encontraremos seus valores y. Veja a tabela.

    \(y=x^2\)
    x y
    0 0
    1 1
    \(−1\) 1
    2 4
    \(−2\) 4

    Observe que quando deixamos\(x=1\) e\(x=−1\), obtemos o mesmo valor para y.

    \[\begin{array} {ll} {y=x^2} &{y=x^2} \\ {y=1^2} &{y=(−1)^2} \\ {y=1} &{y=1} \\ \nonumber \end{array}\]

    A mesma coisa aconteceu quando deixamos\(x=2\)\(x=−2\) e.

    Agora, traçaremos os pontos para mostrar o gráfico de\(y=x^2\). Veja a Figura.

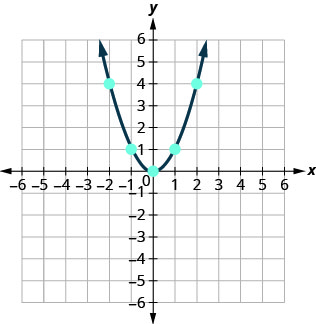
    Esta figura mostra uma curva em forma de u de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O ponto mais baixo da curva está no ponto (0, 0). Outros pontos na curva estão localizados em (-2, 4), (-1, 1), (1, 1) e (2, 4).

    O gráfico não é uma linha. Essa figura é chamada de parábola. Cada equação quadrática tem um gráfico parecido com este.

    No exemplo, você praticará a representação gráfica de uma parábola traçando alguns pontos.

    Exemplo\(\PageIndex{1}\)

    \(y=x^2-1\)

    Resposta

    Representaremos graficamente a equação traçando pontos.


    Escolha valores inteiros para x, substitua-os na equação e resolva por y.    		  
    Registre os valores dos pares ordenados no gráfico. .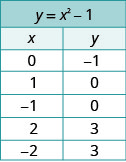
    Faça um gráfico dos pontos e, em seguida, conecte-os com uma curva suave. O resultado será o gráfico da equação\(y=x^2−1\) .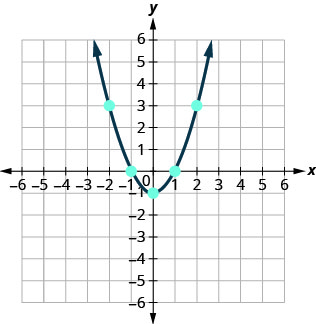
    Exemplo\(\PageIndex{2}\)

    Gráfico\(y=−x^2\).

    Resposta

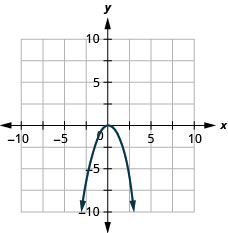
    Esta figura mostra uma curva em forma de u de abertura descendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O ponto mais alto da curva está no ponto (0, 0). Outros pontos na curva estão localizados em (-2, -4), (-1, -1), (1, -1) e (2, -4).

    Exemplo\(\PageIndex{3}\)

    Gráfico\(y=x^2+1\).

    Resposta

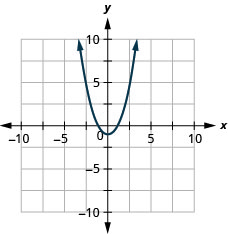
    Esta figura mostra uma curva em forma de u de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O ponto mais baixo da curva está no ponto (0, 1). Outros pontos na curva estão localizados em (-2, 5), (-1, 2), (1, 2) e (2, 5).

    Como fazer as equações\(y=x^2\) e\(y=x^2−1\) differ? What is the difference between their graphs? How are their graphs the same?

    Todas as parábolas do formulário se\(y=ax^2+bx+c\) abrem para cima ou para baixo. Veja a Figura.

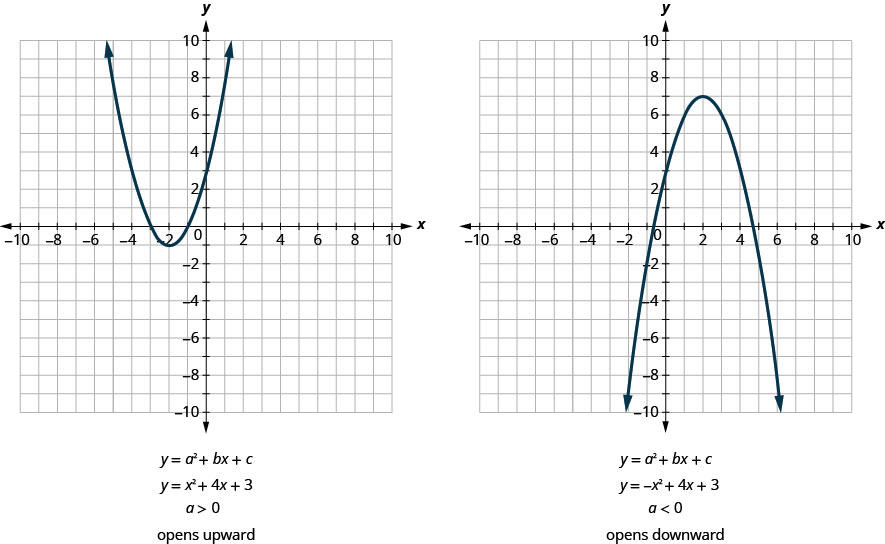
    Esta figura mostra dois gráficos lado a lado. O gráfico no lado esquerdo mostra uma curva em forma de u de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O ponto mais baixo da curva está no ponto (-2, -1). Outros pontos na curva estão localizados em (-3, 0) e (-1, 0). Abaixo do gráfico está a equação y é igual a um quadrado mais b x mais c. Abaixo dessa equação está a equação do gráfico, y é igual a x ao quadrado mais 4 x mais 3. Abaixo disso está a desigualdade maior que 0, o que significa que a parábola se abre para cima. O gráfico no lado direito mostra uma curva em forma de u de abertura descendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O ponto mais alto da curva está no ponto (2, 7). Outros pontos na curva estão localizados em (0, 3) e (4, 3). Abaixo do gráfico está a equação y é igual a um quadrado mais b x mais c. Abaixo dessa equação está a equação do gráfico, y é igual a menos x ao quadrado mais 4 x mais 3. Abaixo disso está a desigualdade menor que 0, o que significa que a parábola se abre para baixo.

    Observe que a única diferença nas duas equações é o sinal negativo antes do\(x^2\) na equação do segundo gráfico na Figura. Quando o\(x^2\) termo é positivo, a parábola se abre para cima e, quando o\(x^2\) termo é negativo, a parábola se abre para baixo.

    Definição: ORIENTAÇÃO DA PARÁBOLA

    Para a equação quadrática\(y=ax^2+bx+c\), se:

    A imagem mostra duas declarações. A primeira afirmação diz “quanto maior que 0, a parábola se abre para cima”. Essa afirmação é seguida pela imagem de uma parábola que se abre para cima. A segunda afirmação diz “a menos de 0, a parábola se abre para baixo”. Essa afirmação é seguida pela imagem de uma parábola que se abre para baixo.
    Exemplo\(\PageIndex{4}\)

    Determine se cada parábola se abre para cima ou para baixo:

    1. \(y=−3x^2+2x−4\)
    2. \( y=6x^2+7x−9\)
    Resposta
     

    .

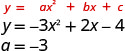
    Como o “a” é negativo, a parábola se abrirá para baixo.
     

    .

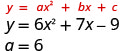
    Como o “a” é positivo, a parábola se abrirá para cima.
    Exemplo\(\PageIndex{5}\)

    Determine se cada parábola se abre para cima ou para baixo:

    1. \(y=2x^2+5x−2\)
    2. \(y=−3x^2−4x+7\)
    Resposta
    1. Para cima
    2. para baixo
    Exemplo\(\PageIndex{6}\)

    Determine se cada parábola se abre para cima ou para baixo:

    1. \(y=−2x^2−2x−3\)
    2. \(y=5x^2−2x−1\)
    Resposta
    1. para baixo
    2. Para cima

    Encontre o eixo de simetria e o vértice de uma parábola

    Veja novamente a Figura. Você vê que poderíamos dobrar cada parábola ao meio e que um lado ficaria em cima do outro? A “linha de dobra” é uma linha de simetria. Nós o chamamos de eixo de simetria da parábola.

    Mostramos os mesmos dois gráficos novamente com o eixo de simetria em vermelho. Veja a Figura.

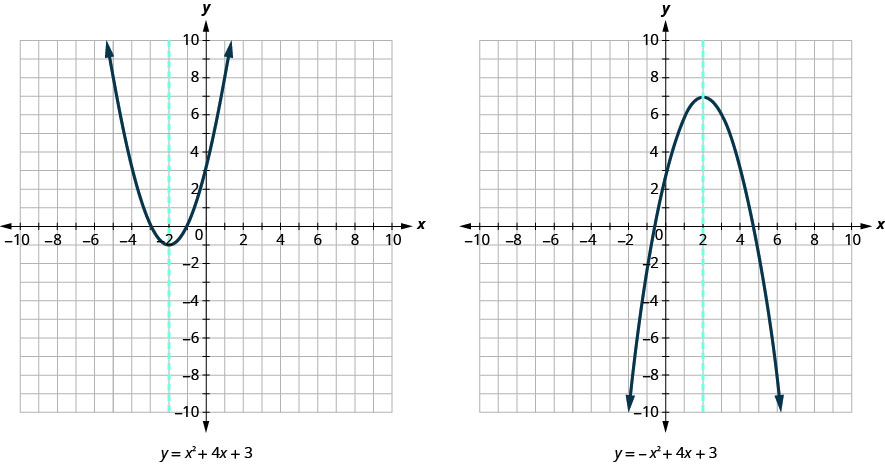
    Esta figura mostra dois gráficos lado a lado. O gráfico no lado esquerdo mostra uma parábola de abertura ascendente representada graficamente no plano da coordenada x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O ponto mais baixo da curva está no ponto (-2, -1). Outros pontos na curva estão localizados em (-3, 0) e (-1, 0). Também no gráfico há uma linha vertical tracejada que passa pelo centro da parábola no ponto (-2, -1). Abaixo do gráfico está a equação do gráfico, y é igual a x ao quadrado mais 4 x mais 3. O gráfico no lado direito mostra uma parábola de abertura para baixo representada graficamente no plano da coordenada x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O ponto mais alto da curva está no ponto (2, 7). Outros pontos na curva estão localizados em (0, 3) e (4, 3). Também no gráfico há uma linha vertical tracejada que passa pelo centro da parábola no ponto (2, 7). Abaixo do gráfico está a equação do gráfico, y é igual a menos x ao quadrado mais 4 x mais 3.

    A equação do eixo de simetria pode ser derivada usando a Fórmula Quadrática. Vamos omitir a derivação aqui e prosseguir diretamente com o uso do resultado. A equação do eixo de simetria do gráfico de\(y=ax^2+bx+c\) é x=\(−\frac{b}{2a}\).

    Então, para encontrar a equação de simetria de cada uma das parábolas que graficamos acima, substituiremos na fórmula x=\(−\frac{b}{2a}\).

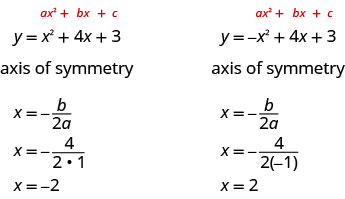
    A figura mostra as etapas para encontrar o eixo de simetria de duas parábolas. No lado esquerdo, a forma padrão de uma equação quadrática que é y igual a x ao quadrado mais b x mais c está escrita acima da equação dada y é igual a x ao quadrado mais 4 x mais 3. O eixo de simetria é a equação x igual a menos b dividida pela quantidade duas vezes a. Inserindo os valores de a e b da equação quadrática, a fórmula se torna x igual a menos 4 dividido pela quantidade 2 vezes 1, o que simplifica para x igual a menos 2. No lado direito, a forma padrão de uma equação quadrática que é y igual a x ao quadrado mais b x mais c está escrita acima da equação dada y é igual a menos x ao quadrado mais 4 x mais 3. O eixo de simetria é a equação x igual a menos b dividida pela quantidade duas vezes a. Inserindo os valores de a e b da equação quadrática, a fórmula se torna x igual a menos 4 dividido pela quantidade 2 vezes -1, o que simplifica para x igual a 2.
    Figura. Essas são as equações das linhas vermelhas tracejadas?

    O ponto na parábola que está no eixo de simetria é o ponto mais baixo ou mais alto da parábola, dependendo se a parábola se abre para cima ou para baixo. Esse ponto é chamado de vértice da parábola.

    Podemos encontrar facilmente as coordenadas do vértice, porque sabemos que ele está no eixo de simetria. Isso significa que sua coordenada x é\(−\frac{b}{2a}\). Para encontrar a coordenada y do vértice, substituímos o valor da coordenada x na equação quadrática.

    A figura mostra as etapas para encontrar o vértice de duas parábolas. No lado esquerdo está a equação dada que y é igual a x ao quadrado mais 4 x mais 3. Abaixo da equação está a afirmação “eixo de simetria é x igual a -2”. Abaixo disso, a declaração “vértice é” ao lado da declaração está um par ordenado com valor x de -2, o mesmo que o eixo de simetria, e o valor y está em branco. Abaixo disso, a equação original é reescrita. Abaixo da equação está a equação com -2 conectado para o valor x, que é y igual a -2 ao quadrado mais 4 vezes -2 mais 3. Isso simplifica para y igual a -1. Abaixo está a afirmação “vértice é (-2, -1)”. No lado direito está a equação dada: y é igual a menos x ao quadrado mais 4 x mais 3. Abaixo da equação está a afirmação “eixo de simetria é x igual a 2”. Abaixo disso, a declaração “vértice é” ao lado da declaração está um par ordenado com valor x de 2, o mesmo que o eixo de simetria, e o valor y está em branco. Abaixo disso, a equação original é reescrita. Abaixo da equação está a equação com 2 conectado para o valor x, que é y igual a menos a quantidade 2 ao quadrado, mais 4 vezes 2 mais 3. Isso simplifica para y igual a 7. Abaixo está a afirmação “vértice é (2, 7)”.

    Definição: EIXO DE SIMETRIA E VÉRTICE DE UMA PARÁBOLA

    Para uma parábola com equação\(y=ax^2+bx+c\):

    • O eixo de simetria de uma parábola é a linha x=\(−\frac{b}{2a}\).
    • O vértice está no eixo de simetria, então sua coordenada x está\(−\frac{b}{2a}\).

    Para encontrar a coordenada y do vértice, substituímos x=\(−\frac{b}{2a}\) na equação quadrática.

    Exemplo\(\PageIndex{7}\)

    Para a parábola,\(y=3x^2−6x+2\) encontre:

    1. o eixo de simetria e
    2. o vértice.
    Resposta
    1. .
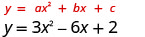
    O eixo de simetria é a linha x=\(−\frac{b}{2a}\) .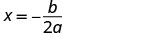
    Substitua os valores de a, b na equação. .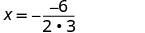
    Simplifique x = 1
      O eixo de simetria é a linha x=1
    2. .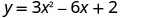
    O vértice está na linha de simetria, então sua coordenada x será x = 1  
    Substitua x=1 na equação e resolva por y. .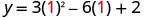
    Simplifique .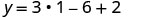
    Essa é a coordenada y. y=−1
    O vértice é (1, −1).
    Exemplo\(\PageIndex{8}\)

    Para a parábola,\(y=2x^2−8x+1\) encontre:

    1. o eixo de simetria e
    2. o vértice.
    Resposta
    1. x=2
    2. (2, −7)
    Exemplo\(\PageIndex{9}\)

    Para a parábola,\(y=2x^2−4x−3\) encontre:

    1. o eixo de simetria e
    2. o vértice.
    Resposta
    1. x = 1
    2. (1, −5)

    Encontre as interceptações de uma parábola

    Quando representamos graficamente equações lineares, frequentemente usamos os interceptos x e y para nos ajudar a representar graficamente as linhas. Encontrar as coordenadas das interceptações também nos ajudará a representar graficamente as parábolas.

    Lembre-se de que, na intercepção y, o valor de x é zero. Então, para encontrar o intercepto y, substituímos x = 0 na equação.

    Vamos encontrar as interceptações y das duas parábolas mostradas na figura abaixo.

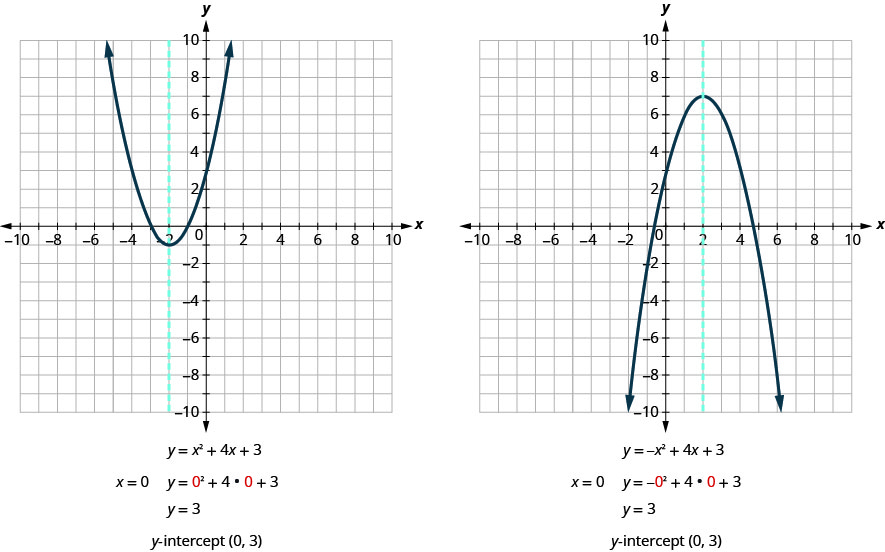
    Esta figura mostra dois gráficos lado a lado. O gráfico no lado esquerdo mostra uma parábola de abertura ascendente representada graficamente no plano da coordenada x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O vértice está no ponto (-2, -1). Outros pontos na curva estão localizados em (-3, 0) e (-1, 0). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x é igual a -2. Abaixo do gráfico está a equação do gráfico, y é igual a x ao quadrado mais 4 x mais 3. Abaixo disso está a afirmação “x é igual a 0”. Ao lado disso está a equação do gráfico com 0 conectado para x, que dá y igual a 0 ao quadrado mais 4 vezes 0 mais 3. Isso simplifica para y igual a 3. Abaixo da equação está a declaração “intercepto y (0, 3)”. O gráfico no lado direito mostra uma parábola de abertura para baixo representada graficamente no plano da coordenada x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O vértice está no ponto (2, 7). Outros pontos na curva estão localizados em (0, 3) e (4, 3). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x igual a 2. Abaixo do gráfico está a equação do gráfico, y é igual a menos x ao quadrado mais 4 x mais 3. Abaixo disso está a afirmação “x é igual a 0”. Ao lado disso está a equação do gráfico com 0 conectado para x, que dá y igual à quantidade negativa 0 ao quadrado mais 4 vezes 0 mais 3. Isso simplifica para y igual a 3. Abaixo da equação está a declaração “intercepto y (0, 3)”.

    Em um intercepto x, o valor de y é zero. Para encontrar um intercepto x, substituímos\(y=0\) a equação. Em outras palavras, precisaremos resolver a equação\(0=ax^2+bx+c\) para x.

    \[\begin{array} {ll} {y=ax^2+bx+c} \\ {0=ax^2+bx+c} \\ \nonumber \end{array}\]

    Mas resolver equações quadráticas como essa é exatamente o que fizemos anteriormente neste capítulo.

    Agora podemos encontrar as interceptações x das duas parábolas mostradas na Figura.

    Primeiro, encontraremos as interceptações x de uma parábola com equação\(y=x^2+4x+3\).

      .
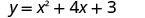    Deixe y = 0 .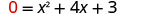
    Fator. .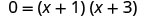
    Use a propriedade zero do produto. .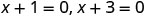
    Resolver. .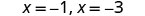
      Os interceptos x são (−1,0) e (−3,0).

    Agora, encontraremos as interceptações x da parábola com a equação\(y=−x^2+4x+3\).

      .
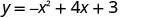    Deixe y = 0 .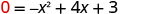
    Essa quadrática não fatora, então usamos a Fórmula Quadrática. .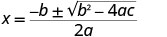
    a=−1, b=4, c=3. .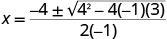
    Simplifique. .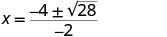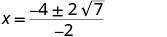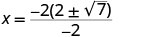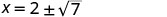
    .
    ..
      As interceptações x são\((2+\sqrt{7},0)\) e\((2−\sqrt{7},0)\)

    Usaremos as aproximações decimais dos interceptos x, para que possamos localizar esses pontos no gráfico.

    \[\begin{array} {l} {(2+\sqrt{7},0) \approx (4.6,0)} & {(2−\sqrt{7},0) \approx (-0.6,0)}\\ \nonumber \end{array}\]

    Esses resultados estão de acordo com nossos gráficos? Veja a Figura.

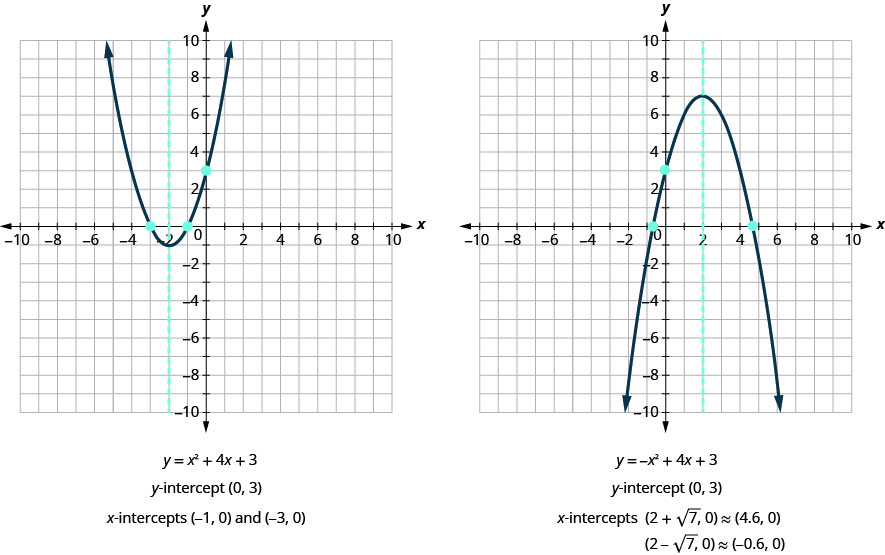
    Esta figura mostra dois gráficos lado a lado. O gráfico no lado esquerdo mostra uma parábola de abertura ascendente representada graficamente no plano da coordenada x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O vértice está no ponto (-2, -1). Três pontos são traçados na curva em (-3, 0), (-1, 0) e (0, 3). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x é igual a -2. Abaixo do gráfico está a equação do gráfico, y é igual a x ao quadrado mais 4 x mais 3. Abaixo disso está a declaração “intercepto y (0, 3)”. Abaixo disso está a declaração “x-intercepta (-1, 0) e (-3, 0)”. O gráfico no lado direito mostra uma parábola de abertura para baixo representada graficamente no plano da coordenada x y. O eixo x do plano vai de menos 10 a 10. O eixo y do plano vai de menos 10 a 10. O vértice está no ponto (2, 7). Três pontos são traçados na curva em (-0,6, 0), (4,6, 0) e (0, 3). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x igual a 2. Abaixo do gráfico está a equação do gráfico, y é igual a menos x ao quadrado mais 4 x mais 3. Abaixo disso está a declaração “intercepto y (0, 3)”. Abaixo disso está a afirmação “interceptos x (2 mais raiz quadrada de 7, 0) é aproximadamente igual a (4,6, 0) e (2 menos raiz quadrada de 7, 0) é aproximadamente igual a (-0,6, 0)”.
    Definição: ENCONTRE AS INTERCEPTAÇÕES DE UMA PARÁBOLA

    Para encontrar os interceptos de uma parábola com a equação\(y=ax^2+bx+c\):

    \[\begin{array}{ll} {\textbf{y-intercept}}& {\textbf{x-intercept}}\\ {\text{Let} x=0 \text{and solve the y}}& {\text{Let} y=0 \text{and solve the x}}\\ \nonumber \end{array}\]

    Exemplo\(\PageIndex{10}\)

    Encontre as interceptações da parábola\(y=x^2−2x−8\).

    Resposta
      .
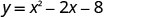
    Para encontrar o intercepto y, deixe x=0 e resolva por y. .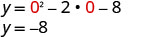
      Quando x=0, então y=−8.
    O intercepto y é o ponto (0, −8).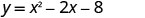
      .
    Para encontrar o intercepto x, deixe y = 0 e resolva para x. .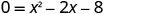
    Resolva por fatoração. .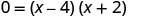
     

    .
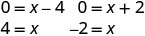
    Quando y=0, então x=4 ou x=−2. Os interceptos x são os pontos (4,0) e (−2,0).
    Exemplo\(\PageIndex{11}\)

    Encontre as interceptações da parábola\(y=x^2+2x−8\).

    Resposta

    y: (0, −8); x: (−4,0), (2,0)

    Exemplo\(\PageIndex{12}\)

    Encontre as interceptações da parábola\(y=x^2−4x−12\).

    Resposta

    y: (0, −12); x: (6,0), (−2,0)

    Neste capítulo, resolvemos equações quadráticas da forma\(ax^2+bx+c=0\). Resolvemos para xx e os resultados foram as soluções para a equação.

    Agora estamos analisando equações quadráticas em duas variáveis do formulário\(y=ax^2+bx+c\). Os gráficos dessas equações são parábolas. As interceptações x das parábolas ocorrem onde y = 0.

    Por exemplo:

    \[\begin{array}{cc} {\textbf{Quadratic equation}}&{\textbf{Quadratic equation in two variable}}\\ {}&{y=x^2−2x−15}\\ {x^2−2x−15}&{\text{Let} y=0, 0=x^2−2x−15}\\ {(x−5)(x+3)=0}&{0=(x−5)(x+3)}\\ {x−5=0, x+3=0}&{x−5=0, x+3=0}\\ {x=5, x=−3}&{x=5, x=−3}\\ {}&{(5,0) \text{and} (−3,0)}\\ {}&{\text{x-intercepts}}\\ \end{array}\]

    As soluções da equação quadrática são os valores x dos interceptos x.

    Anteriormente, vimos que as equações quadráticas têm soluções 2, 1 ou 0. Os gráficos abaixo mostram exemplos de parábolas para esses três casos. Como as soluções das equações fornecem as interceptações x dos gráficos, o número de interceptações x é o mesmo que o número de soluções.

    Anteriormente, usamos o discriminante para determinar o número de soluções de uma equação quadrática da forma\(ax^2+bx+c=0\). Agora, podemos usar o discriminante para nos dizer quantas interceptações x existem no gráfico.

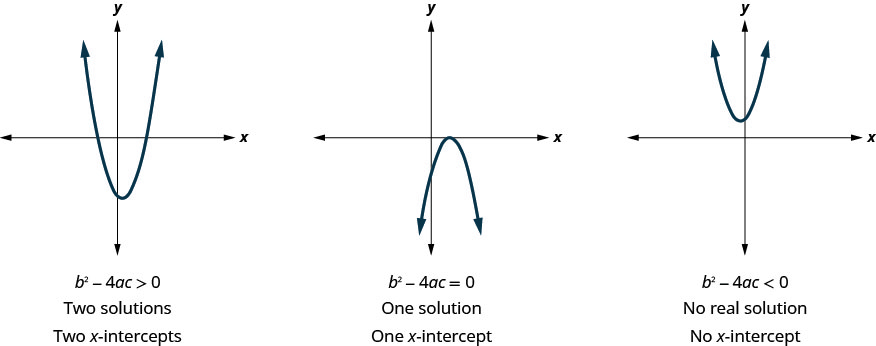
    Esta figura mostra três gráficos lado a lado. O gráfico mais à esquerda mostra uma parábola de abertura ascendente representada graficamente no plano da coordenada x y. O vértice da parábola está no quadrante inferior direito. Abaixo do gráfico está a desigualdade b ao quadrado menos 4 a c maior que 0. Abaixo está a declaração “Duas soluções”. Abaixo disso está a declaração “Duas interceptações x”. O gráfico do meio mostra uma parábola de abertura descendente representada graficamente no plano da coordenada x y. O vértice da parábola está no eixo x. Abaixo do gráfico está a equação b ao quadrado menos 4 a c é igual a 0. Abaixo está a afirmação “Uma solução”. Abaixo disso está a declaração “One x-intercept”. O gráfico mais à direita mostra uma parábola de abertura ascendente representada graficamente no plano da coordenada x y. O vértice da parábola está no quadrante superior esquerdo. Abaixo do gráfico está a desigualdade b ao quadrado menos 4 a c menor que 0. Abaixo está a afirmação “Nenhuma solução real”. Abaixo disso está a declaração “Sem interceptação x”.

    Antes de começar a resolver a equação quadrática para encontrar os valores dos interceptos x, talvez você queira avaliar o discriminante para saber quantas soluções esperar.

    Exemplo\(\PageIndex{13}\)

    Encontre as interceptações da parábola\(y=5x^2+x+4\).

    Resposta
      .
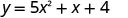
    Para encontrar o intercepto y, deixe x=0 e resolva por y. .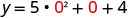
    .
    Quando x=0, então y=4.
    O intercepto y é o ponto (0,4).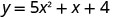
      .
    Para encontrar o intercepto x, deixe y = 0 e resolva para x. .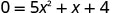
    Encontre o valor do discriminante para prever o número de soluções e, portanto, x -intercepta.

    b^2−4ac

    1^2−4⋅5⋅4

    1−80

    −79
    Como o valor do discriminante é negativo, não há uma solução real para a equação. Não há interceptações x.
    Exemplo\(\PageIndex{14}\)

    Encontre as interceptações da parábola\(y=3x^2+4x+4\).

    Resposta

    y: (0,4); x: nenhum

    Exemplo\(\PageIndex{15}\)

    Encontre as interceptações da parábola\(y=x^2−4x−5\).

    Resposta

    y: (0, −5); x: (5,0) (−1,0)

    Exemplo\(\PageIndex{16}\)

    Encontre as interceptações da parábola\(y=4x^2−12x+9\).

    Resposta
      .
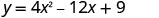
    Para encontrar o intercepto y, deixe x=0 e resolva por y. .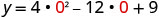
    .
      Quando x=0, então y=9.
    O intercepto y é o ponto (0,9).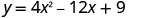
      .
    Para encontrar o intercepto x, deixe y = 0 e resolva para x. .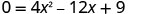
    Encontre o valor do discriminante para prever o número de soluções e, portanto, x -intercepta.

    b^2−4ac

    12^2−4⋅4⋅9

    144 a 144

    0
      Como o valor do discriminante é 0, não há uma solução real para a equação. Portanto, há um intercepto x.
    Resolva a equação fatorando o trinômio quadrado perfeito. .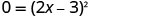
    Use a propriedade Zero Product. .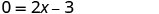
    Resolva para x. .
    .
      Quando y=0, então\(\frac{3}{2}\) =x.
      O intercepto x é o ponto\((\frac{3}{2},0)\).
    Exemplo\(\PageIndex{17}\)

    Encontre as interceptações da parábola\(y=−x^2−12x−36.\).

    Resposta

    y: (0, −36); x: (−6,0)

    Exemplo\(\PageIndex{18}\)

    Encontre as interceptações da parábola\(y=9x^2+12x+4\).

    Resposta

    y: (0,4); x:\((−\frac{2}{3},0)\)

    Representar graficamente equações quadráticas em duas variáveis

    Agora, temos todas as peças que precisamos para representar graficamente uma equação quadrática em duas variáveis. Só precisamos juntá-los. No próximo exemplo, veremos como fazer isso.

    Como representar graficamente uma equação quadrática em duas variáveis

    Exemplo\(\PageIndex{19}\)

    Gráfico\(y=x2−6x+8\).

    Resposta

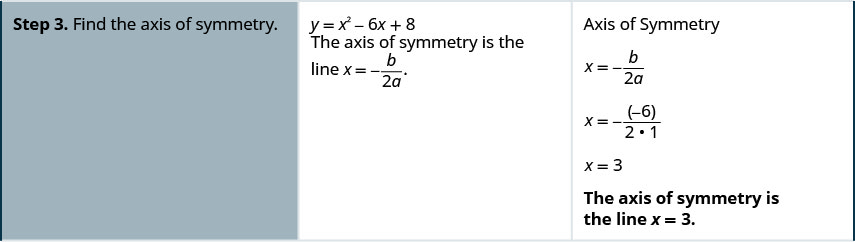
    A imagem mostra as etapas para representar graficamente a equação quadrática y é igual a x ao quadrado menos 6 x mais 8. O passo 1 é escrever a equação quadrática com y em um lado. Essa equação já tem y em um lado. O valor de a é um, o valor de b é -6 e o valor de c é 8.O passo 2 é determinar se a parábola se abre para cima ou para baixo. Como a é positivo, a parábola se abre para cima.O passo 3 é encontrar o eixo de simetria. O eixo de simetria é a linha x igual a menos b dividida pela quantidade 2 a. Inserindo os valores de b e a, a fórmula se torna x igual a menos -6 dividido pela quantidade 2 vezes 1, o que simplifica para x igual a 3. O eixo de simetria é a linha x igual a 3.O passo 4 é encontrar o vértice. O vértice está no eixo de simetria. Substitua x igual a 3 na equação e resolva por y. A equação é y igual a x ao quadrado menos 6 x mais 8. Substituindo x por 3, ele se torna y igual a 3 ao quadrado menos 6 vezes 3 mais 8, o que simplifica para y igual a -1. O vértice é (3, -1).A etapa 5 é encontrar o intercepto y e encontrar o ponto simétrico ao intercepto y no eixo de simetria. Substituímos x igual a 0 na equação. A equação é y igual a x ao quadrado menos 6 x mais 8. Substituindo x por 0, ele se torna y igual a 0 ao quadrado menos 6 vezes 0 mais 8, o que simplifica para y igual a 8. O intercepto y é (0, 8). Usamos o eixo de simetria para encontrar um ponto simétrico ao intercepto y. O intercepto y está 3 unidades à esquerda do eixo de simetria, x é igual a 3. Um ponto 3 unidades à direita do eixo de simetria tem x igual a 6. O ponto simétrico ao intercepto y é (6, 8).O passo 6 é encontrar os interceptos x. Substituímos y igual a 0 na equação. A equação se torna 0 igual a x ao quadrado menos 6 x mais 8. Podemos resolver essa equação quadrática fatorando para obter 0 igual à quantidade x menos 2 vezes a quantidade x menos 4. Resolva cada equação para obter x igual a 2 e x igual a 4. Os interceptos x são (2, 0) e (4, 0).O passo 7 é representar graficamente a parábola. Representamos graficamente o vértice, os interceptos e o ponto simétrico ao intercepto y. Conectamos esses cinco pontos para esboçar a parábola. O gráfico mostra uma parábola de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de -2 a 10. O eixo y do plano vai de -3 a 10. O vértice está no ponto (3, -1). Quatro pontos são traçados na curva em (0, 8), (6, 8), (2, 0) e (4, 0). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x igual a 3.

    Exemplo\(\PageIndex{20}\)

    Representar graficamente a parábola\(y=x^2+2x−8\).

    Resposta

    y: (0, −8); x: (2,0), (−4,0);
    eixo: x=−1; vértice: (−1, −9);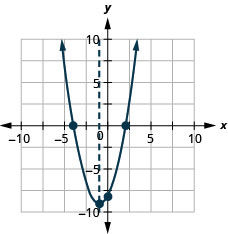

    O gráfico mostra uma parábola de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do avião vai de -10 a 10. O eixo y do plano vai de -10 a 10. O vértice está no ponto (-1, -9). Três pontos são traçados na curva em (0, -8), (2, 0) e (-4, 0). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x é igual a -1.
    Exemplo\(\PageIndex{21}\)

    Faça um gráfico da parábola\(y=x^2−8x+12\).

    Resposta

    y: (0,12); x: (2,0), (6,0);
    eixo: x=4; vértice :( 4, −4);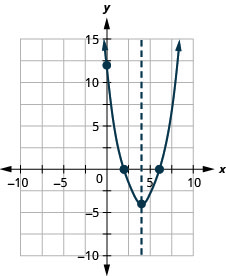

    O gráfico mostra uma parábola de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do avião vai de -10 a 10. O eixo y do plano vai de -10 a 10. O vértice está no ponto (4, -4). Três pontos são traçados na curva em (0, 12), (2, 0) e (6, 0). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x igual a 4.
    Definição: REPRESENTAR GRAFICAMENTE UMA EQUAÇÃO QUADRÁTICA EM DUAS VARIÁVEIS.
    1. Escreva a equação quadrática com yy em um lado.
    2. Determine se a parábola se abre para cima ou para baixo.
    3. Encontre o eixo de simetria.
    4. Encontre o vértice.
    5. Encontre o intercepto y. Encontre o ponto simétrico ao intercepto y no eixo de simetria.
    6. Encontre as interceptações x.
    7. Faça um gráfico da parábola.

    Conseguimos encontrar as interceptações x no último exemplo por meio de fatoração. Encontramos as interceptações x no próximo exemplo também fatorando.

    Exemplo\(\PageIndex{22}\)

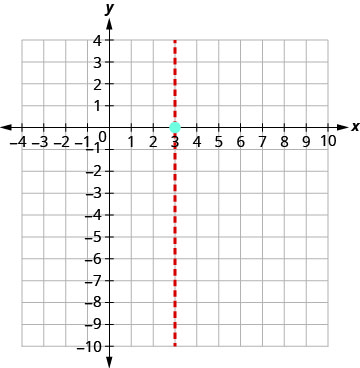
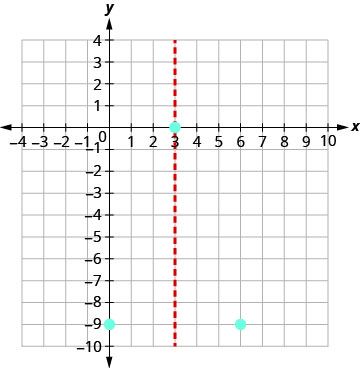
    Gráfico\(y=−x^2+6x−9\).

    Resposta
    A equação y tem de um lado. .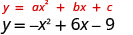
    Como a é −1, a parábola se abre para baixo.

    Para encontrar o eixo de simetria, encontre\(x=−\frac{b}{2a}\).    		 . .
    .
    .

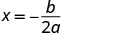
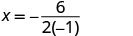
    O eixo de simetria é x=3. O vértice está na linha x=3.

    .

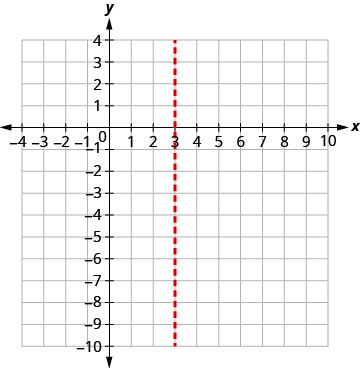
    Encontre y quando x = 3.    		 .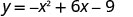
    .
    .
    .
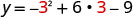
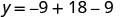
    O vértice é (3,0).

    .
    O intercepto y ocorre quando x=0.
    Substitua x=0.
    Simplifique.

    O ponto (0, −9) é três unidades à esquerda da linha de simetria.
    O ponto três unidades à direita da linha de simetria é (6, −9).
    O ponto simétrico ao intercepto y é (6, −9)    		 .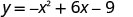
    .
    .
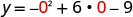
    (0, −9).
    .
    O intercepto x ocorre quando y = 0. .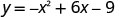
    Substitua y=0. .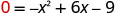
    Considere o GCF. .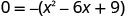
    Considere o trinômio. .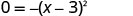
    Resolva para x. .
    Conecte os pontos para representar graficamente a parábola. .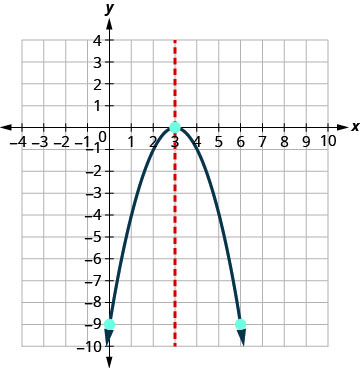
    Exemplo\(\PageIndex{23}\)

    Faça um gráfico da parábola\(y=−3x^2+12x−12\).

    Resposta

    y: (0, −12); x: (2,0);
    eixo: x=2; vértice :( 2,0);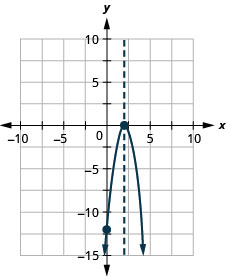

    O gráfico mostra uma parábola de abertura descendente representada graficamente no plano de coordenadas x y. O eixo x do avião vai de -10 a 10. O eixo y do plano vai de -1 a 10. O vértice está no ponto (2, 0). Um outro ponto é traçado na curva em (0, -12). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x igual a 2.

    Exemplo\(\PageIndex{24}\)

    Faça um gráfico da parábola\(y=25x^2+10x+1\).

    Resposta

    y: (0,1); x: (−15,0);
    eixo: x=−15; vértice :( −15,0);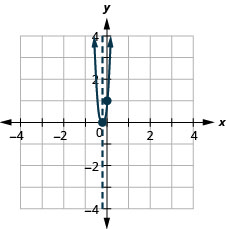

    O gráfico mostra uma parábola de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de -5 a 5. O eixo y do plano vai de -5 a 10. O vértice está no ponto (-1 quinto, 0). Um outro ponto é traçado na curva em (0, 1). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x é igual a -1 quinto.

    Para o gráfico de\(y=−x^2+6x−9\) the vertex and the x -intercepto eram o mesmo ponto. Lembra como o discriminante determina o número de soluções de uma equação quadrática? O discriminante da equação\(0=−x^2+6x−9\) is 0, so there is only one solution. That means there is only one x -intercepta, e é o vértice da parábola.

    Quantas interceptações x você esperaria ver no gráfico de\(y=x^2+4x+5\)?

    Exemplo\(\PageIndex{25}\)

    Gráfico\(y=x^2+4x+5\).

    Resposta
    A equação tem y em um lado. .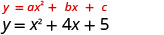
    Como a é 1, a parábola se abre para cima. .
    \(x=−\frac{b}{2a}\). .
    .
    .
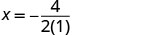
    x=−2.
    .
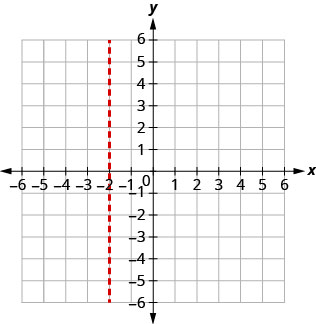
    O vértice está na linha x=−2.  
    Encontre y quando x=−2. .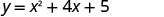
    .
    .
    .
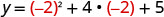
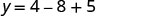
    (−2,1).
    .
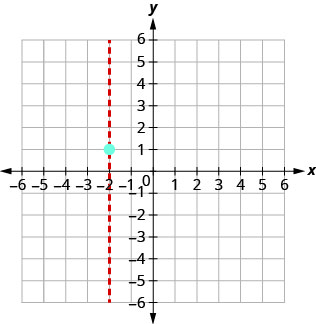
    O intercepto y ocorre quando x=0.
    Substitua x=0.
    Simplifique.
    O ponto (0,5) é duas unidades à direita da linha de simetria.
    O ponto duas unidades à esquerda da linha de simetria é (−4,5).    		 .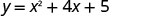
    .
    .
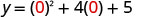
    (0,5).
    .
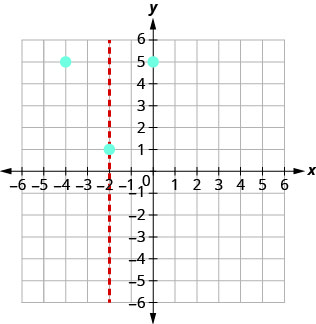
    (−4,5)
    O intercepto x ocorre quando y=0.
    Substitua y=0.
    Teste o discriminante.    		 .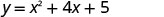
    .
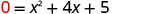
        \(b^2−4ac\)
    \(42−4⋅15\)
    \(16−20\)
    \(−4\)
    Como o valor do discriminante é negativo, não há solução e, portanto, não há interceptação x.
    Conecte os pontos para representar graficamente a parábola. Você pode escolher mais dois pontos para maior precisão.    		 .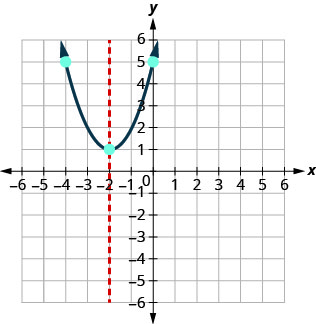
    Exemplo\(\PageIndex{26}\)

    Faça um gráfico da parábola\(y=2x^2−6x+5\).

    Resposta

    y: (0,5); x:nenhum;
    eixo:\(x=\frac{3}{2}\); vértice:\((\frac{3}{2},\frac{1}{2})\);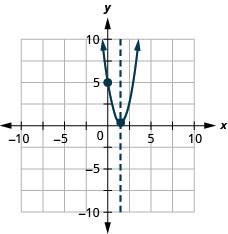

    O gráfico mostra uma parábola de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de -5 a 5. O eixo y do plano vai de -5 a 10. O vértice está no ponto (3 metades, 1 metade). Um outro ponto é traçado na curva em (0, 5). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x é igual a 3 metades.

    Exemplo\(\PageIndex{27}\)

    Faça um gráfico da parábola\(y=−2x^2−1\).

    Resposta

    y: (0, −1); x:nenhum;
    eixo: x=0; vértice :( 0, −1);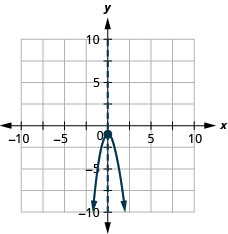

    O gráfico mostra uma parábola de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do avião vai de -10 a 10. O eixo y do plano vai de -10 a 10. O vértice está no ponto (0, -1). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x igual a 0.

    Encontrar o intercepto y substituindo x=0 na equação é fácil, não é? Mas precisávamos usar a Fórmula Quadrática para encontrar os interceptos x em Example. Usaremos a Fórmula Quadrática novamente no próximo exemplo.

    Exemplo\(\PageIndex{28}\)

    Gráfico\(y=2x^2−4x−3\).

    Resposta
      .
    A equação y tem um lado.
    Como a é 2, a parábola se abre para cima.    		 .
    Para encontrar o eixo de simetria, encontre\(x=−\frac{b}{2a}\) .
    .
    .
    O vértice é x=1
    O vértice na linha x=1. .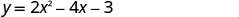
    Encontre y quando x = 1 .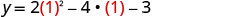
    .
    .
    (1, −5)
    O intercepto y ocorre quando x=0. .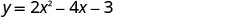
    Substitua x=0. .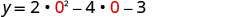
    Simplifique. .
    O intercepto y é (0, −3)

    O ponto (0, −3) é uma unidade à esquerda da linha de simetria.
    O ponto uma unidade à direita da linha de simetria é (2, −3)    		 O ponto simétrico ao intercepto y é (2, −3).
    O intercepto x ocorre quando y = 0 .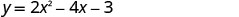
    Substitua y=0 .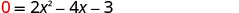
    Use a fórmula quadrática. .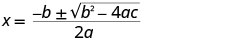
    Substitua os valores de a, b, c. .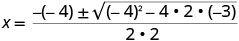
    Simplifique. .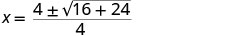
    Simplifique o interior do radical. .
    Simplifique o radical. .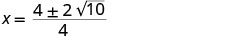
    Considere o GCF. .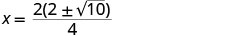
    Remova os fatores comuns. .
    Escreva como duas equações. .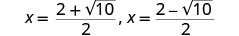
    Aproxime os valores. .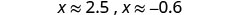
     
    Os valores aproximados dos interceptos x são (2,5,0) e (−0,6,0).
    Faça um gráfico da parábola usando os pontos encontrados. .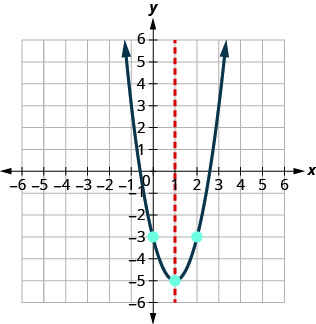
    Exemplo\(\PageIndex{29}\)

    Faça um gráfico da parábola\(y=5x^2+10x+3\).

    Resposta

    y: (0,3); x: (−1,6,0), (−0,4,0);
    eixo: x=−1; vértice :( −1, −2);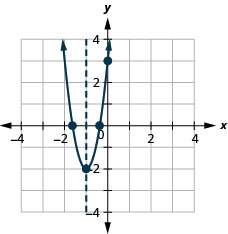

    O gráfico mostra uma parábola de abertura ascendente representada graficamente no plano de coordenadas x y. O eixo x do plano vai de -5 a 5. O eixo y do plano vai de -5 a 5. O vértice está no ponto (-1, -2). Três outros pontos são traçados na curva em (0, 3), (-1,6, 0), (-0,4, 0). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x é igual a -1.

    Exemplo\(\PageIndex{30}\)

    Faça um gráfico da parábola\(y=−3x^2−6x+5\).

    Resposta

    y: (0,5); x: (0,6,0), (−2,6,0);
    eixo: x=−1; vértice :( −1,8);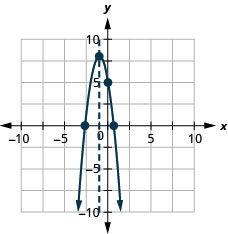

    O gráfico mostra uma parábola de abertura descendente representada graficamente no plano de coordenadas x y. O eixo x do avião vai de -10 a 10. O eixo y do plano vai de -10 a 10. O vértice está no ponto (-1, 8). Três outros pontos são traçados na curva em (0, 5), (0,6, 0) e (-2,6, 0). Também no gráfico há uma linha vertical tracejada representando o eixo de simetria. A linha passa pelo vértice em x é igual a -1.

    Resolva aplicações máximas e mínimas

    Saber que o vértice de uma parábola é o ponto mais baixo ou mais alto da parábola nos dá uma maneira fácil de determinar o valor mínimo ou máximo de uma equação quadrática. A coordenada y do vértice é o valor mínimo y de uma parábola que se abre para cima. É o valor máximo de y de uma parábola que se abre para baixo. Veja a Figura.

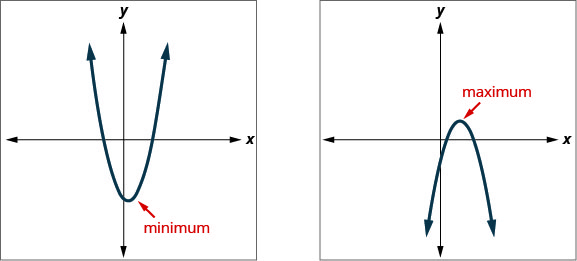
    Esta figura mostra dois gráficos lado a lado. O gráfico à esquerda mostra uma parábola de abertura descendente representada graficamente no plano da coordenada x y. O vértice da parábola está no quadrante superior direito. O vértice é rotulado como “máximo”. O gráfico à direita mostra uma parábola de abertura ascendente representada graficamente no plano da coordenada x y. O vértice da parábola está no quadrante inferior direito. O vértice é rotulado como “mínimo”.
    Definição: VALORES MÍNIMOS OU MÁXIMOS DE UMA EQUAÇÃO QUADRÁTICA

    A coordenada y do vértice do gráfico de uma equação quadrática é

    • valor mínimo da equação quadrática se a parábola se abrir para cima.
    • valor máximo da equação quadrática se a parábola se abrir para baixo.
    Exemplo\(\PageIndex{31}\)

    Encontre o valor mínimo da equação quadrática\(y=x^2+2x−8\).

    Resposta
      .
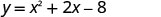
    Como a é positivo, a parábola se abre para cima.  
    A equação quadrática tem um mínimo.  
    Encontre o eixo de simetria. .
    .
    .
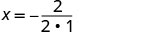
    x=−1
    O vértice está na linha x=−1. .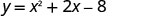
    Encontre y quando x=−1. .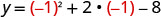
    .
    .
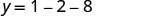
    (−1, −9)
    Como a parábola tem um mínimo, a coordenada y do vértice é o valor mínimo y da equação quadrática.  
    O valor mínimo da quadrática é −9 e ocorre quando x=−1.  
    Mostre o gráfico para verificar o resultado. .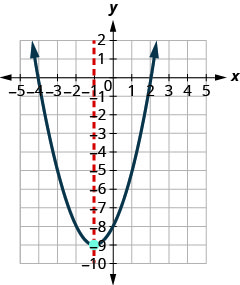
    Exemplo\(\PageIndex{32}\)

    Encontre o valor máximo ou mínimo da equação quadrática\(y=x^2−8x+12\).

    Resposta

    O valor mínimo é −4 quando x=4.

    Exemplo\(\PageIndex{33}\)

    Encontre o valor máximo ou mínimo da equação quadrática\(y=−4x^2+16x−11\).

    Resposta

    O valor máximo é 5 quando x=2.

    Usamos a fórmula

    \[\begin{array} {l} {h=−16t^2+v_{0}t+h_{0}}\\ \nonumber \end{array}\]

    para calcular a altura em pés, h, de um objeto lançado no ar com velocidade inicial,\(v_{0}\), após t segundos.

    Essa fórmula é uma equação quadrática na variável tt, então seu gráfico é uma parábola. Ao resolver as coordenadas do vértice, podemos descobrir quanto tempo o objeto levará para atingir sua altura máxima. Então, podemos calcular a altura máxima.

    Exemplo\(\PageIndex{34}\)

    A equação quadrática\(h=−16t^2+v_{0}t+h_{0}\) modela a altura de uma bola de vôlei atingida diretamente para cima com velocidade de 176 pés por segundo a partir de uma altura de 4 pés.

    1. Quantos segundos o voleibol levará para atingir sua altura máxima?
    2. Encontre a altura máxima do voleibol.
    Resposta

    \(h=−16t^2+176t+4\)

    Como a é negativo, a parábola se abre para baixo.

    A equação quadrática tem um máximo.

    1.
    \[\begin{array} {ll} {}&{t=−\frac{b}{2a}}\\ {\text{Find the axis of symmetry.}}& {t=−\frac{176}{2(−16)}}\\ {}&{t=5.5}\\ {}&{\text{The axis of symmetry is} t = 5.5}\\ {\text{The vertex is on the line} t=5.5}& {\text{The maximum occurs when} t =5.5 \text{seconds.}}\\ \nonumber \end{array}\]

    2.

    Encontre h quando t = 5,5. .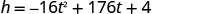
    .
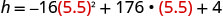
    Use uma calculadora para simplificar. .
      O vértice é (5.5.488)
    Como a parábola tem um máximo, a coordenada h do vértice é o valor máximo y da equação quadrática. O valor máximo da quadrática é 488 pés e ocorre quando t = 5,5 segundos.
    Exemplo\(\PageIndex{35}\)

    A equação quadrática\(h=−16t^2+128t+32\) é usada para encontrar a altura de uma pedra lançada para cima de uma altura de 32 pés a uma taxa de 128 pés/seg. Quanto tempo demorará para a pedra atingir sua altura máxima? Qual é a altura máxima? Arredonde as respostas para o décimo mais próximo.

    Resposta

    Levará 4 segundos para atingir a altura máxima de 288 pés.

    Exemplo\(\PageIndex{36}\)

    Um foguete de brinquedo disparado do solo a uma taxa de 208 pés/seg tem a equação quadrática de\(h=−16t^2+208t\). Quando o foguete atingirá sua altura máxima? Qual será a altura máxima? Arredonde as respostas para o décimo mais próximo.

    Resposta

    Levará 6,5 segundos para atingir a altura máxima de 676 pés.

    Acesse esses recursos on-line para obter instruções adicionais e praticar a representação gráfica de equações quadráticas:

    Conceitos-chave

    • O gráfico de cada equação quadrática é uma parábola.
    • Orientação da parábola Para a equação quadrática\(y=ax^2+bx+c\), se
      • a>0, a parábola se abre para cima.
      • a<0, a parábola se abre para baixo.
    • Eixo de simetria e vértice de uma parábola Para uma parábola com equação\(y=ax^2+bx+c\):
      • O eixo de simetria de uma parábola é a linha\(x=−\frac{b}{2a}\).
      • O vértice está no eixo de simetria, então sua coordenada x está\(−\frac{b}{2a}\).
      • Para encontrar a coordenada y do vértice,\(x=−\frac{b}{2a}\) substituímos a equação quadrática.
    • Encontre as interceptações de uma parábola Para encontrar as interceptações de uma parábola com a equação\(y=ax^2+bx+c\):
      \[\begin{array} {ll} {\textbf{y-intercept}}&{\textbf{x-intercepts}}\\ {\text{Let} x=0 \text{and solve for y}}&{\text{Let} y=0 \text{and solve for x}}\\ \nonumber \end{array}\]
    • Para representar graficamente uma equação quadrática em duas variáveis
      1. Escreva a equação quadrática com yy em um lado.
      2. Determine se a parábola se abre para cima ou para baixo.
      3. Encontre o eixo de simetria.
      4. Encontre o vértice.
      5. Encontre o intercepto y. Encontre o ponto simétrico ao intercepto y no eixo de simetria.
      6. Encontre as interceptações x.
      7. Faça um gráfico da parábola.
    • Valores mínimos ou máximos de uma equação quadrática
      • A coordenada y do vértice do gráfico de uma equação quadrática é
      • valor mínimo da equação quadrática se a parábola se abrir para cima.
      • valor máximo da equação quadrática se a parábola se abrir para baixo.

    Glossário

    eixo de simetria
    O eixo de simetria é a linha vertical que passa pelo meio da parábola\(y=ax^2+bx+c\).
    parábola
    O gráfico de uma equação quadrática em duas variáveis é uma parábola.
    equação quadrática em duas variáveis
    Uma equação quadrática em duas variáveis, onde a, b e c são números reais e\(a \ge 0\) é uma equação da forma\(y=ax^2+bx+c\).
    vértice
    O ponto na parábola que está no eixo de simetria é chamado de vértice da parábola; é o ponto mais baixo ou mais alto da parábola, dependendo se a parábola se abre para cima ou para baixo.
    x -interceptações de uma parábola
    Os interceptos x são os pontos na parábola onde\(y=0\).
    y -interceptação de uma parábola
    O intercepto y é o ponto na parábola onde\(x=0\).