7.6: Equações quadráticas
- Page ID
- 184146
Ao final desta seção, você poderá:
- Resolva equações quadráticas usando a Propriedade do Produto Zero
- Resolva a fatoração de equações quadráticas
- Resolva aplicações modeladas por equações quadráticas
Antes de começar, faça este teste de prontidão.
- Resolver:\(5y−3=0\).
Se você perdeu esse problema, revise o Exercício 2.3.1. - Resolver:\(10a=0\).
Se você perdeu esse problema, revise o Exercício 2.2.1. - Combine termos semelhantes:\(12 x^{2}-6 x+4 x\).
Se você perdeu esse problema, revise o Exercício 1.3.37. - Fator\(n^{3}-9 n^{2}-22 n\) completamente.
Se você perdeu esse problema, revise o Exercício 7.3.10.
Já resolvemos equações lineares, equações da forma\(a x+b y=c\). Em equações lineares, as variáveis não têm expoentes. Equações quadráticas são equações nas quais a variável é quadrada. Listados abaixo estão alguns exemplos de equações quadráticas:
\[x^{2}+5 x+6=0 \quad 3 y^{2}+4 y=10 \quad 64 u^{2}-81=0 \quad n(n+1)=42\]
A última equação não parece ter a variável ao quadrado, mas quando simplificarmos a expressão à esquerda, obteremos\(n^{2}+n\).
A forma geral de uma equação quadrática é\(a x^{2}+b x+c=0\), com\(a \neq 0\).
Uma equação da forma\(a x^{2}+b x+c=0\) é chamada de equação quadrática.
\[a, b, \text { and } c \text { are real numbers and } a \neq 0\]
Para resolver equações quadráticas, precisamos de métodos diferentes dos que usamos na solução de equações lineares. Examinaremos um método aqui e, em seguida, vários outros em um capítulo posterior.
Resolva equações quadráticas usando a propriedade de produto zero
Primeiro, resolveremos algumas equações quadráticas usando a Propriedade do Produto Zero. A Propriedade do Produto Zero diz que se o produto de duas quantidades for zero, deve ser que pelo menos uma das quantidades seja zero. A única maneira de obter um produto igual a zero é multiplicar pelo próprio zero.
\(\text { If } a \cdot b=0, \text { then either } a=0 \text { or } b=0 \text { or both. }\)
Agora usaremos a Propriedade do Produto Zero para resolver uma equação quadrática.
Resolver:\((x+1)(x-4)=0\)
- Resposta
-



Resolver:\((x-3)(x+5)=0\)
- Resposta
-
\(x=3, x=-5\)
Resolver:\((y-6)(y+9)=0\)
- Resposta
-
\(y=6, y=-9\)
Normalmente, trabalharemos um pouco mais do que neste último exemplo para resolver as equações lineares resultantes do uso da Propriedade do Produto Zero.
Resolver:\((5 n-2)(6 n-1)=0\)
- Resposta
-
\((5 n-2)(6 n-1)=0\) Use a Propriedade do Produto Zero para definir
cada fator como 0.\(5 n-2=0 \)
\(6 n-1=0\) Resolva as equações. \(n=\frac{2}{5}\) \(n = \frac{1}{6}\) Verifique suas respostas. 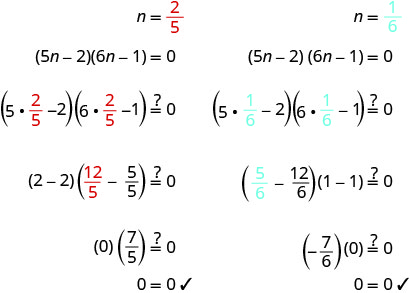
Resolver:\((3 m-2)(2 m+1)=0\)
- Resposta
-
\(m=\frac{2}{3}, m=-\frac{1}{2}\)
Resolver:\((4 p+3)(4 p-3)=0\)
- Resposta
-
\(p=-\frac{3}{4}, p=\frac{3}{4}\)
Observe, quando verificamos as soluções, que cada uma delas produziu apenas um fator igual a zero. Mas o produto foi zero para ambas as soluções.
Resolver:\(3 p(10 p+7)=0\)
- Resposta
-
\(3p(10p+7)=0\) Use a Propriedade do Produto Zero para definir
cada fator como 0.3p=0 10p+7 = 0 Resolva as equações. p=0 10p=−7 \(p=-\frac{7}{10}\) Verifique suas respostas. 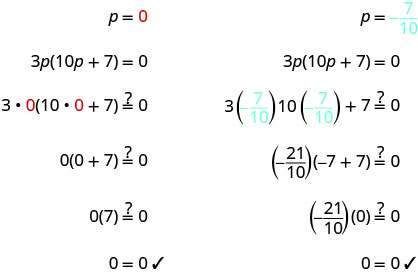
Resolver:\(2 u(5 u-1)=0\)
- Resposta
-
\(u=0, u=\frac{1}{5}\)
Resolver:\(w(2 w+3)=0\)
- Resposta
-
\(w=0, w=-\frac{3}{2}\)
Pode parecer que há apenas um fator no próximo exemplo. Lembre-se, no entanto, que isso\((y-8)^{2}\) significa\((y-8)(y-8)\).
Resolver:\((y-8)^{2}=0\)
- Resposta
-
\((y−8)^{2}=0\) Reescreva o lado esquerdo como um produto. (y−8) (y−8) =0 Use a Propriedade do Produto Zero e
defina cada fator como 0.y−8=0 y−8=0 Resolva as equações. y = 8 y = 8 Quando uma solução se repete, nós a chamamos
de raiz dupla.Verifique sua resposta. 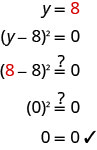
Resolver:\((x+1)^{2}=0\)
- Resposta
-
\(x=1\)
Resolver:\((v-2)^{2}=0\)
- Resposta
-
\(v=2\)
Resolva equações quadráticas por fatoração
Cada uma das equações que resolvemos nesta seção até agora tinha um lado na forma fatorada. Para usar a Propriedade do Produto Zero, a equação quadrática deve ser fatorada, com zero em um lado. Portanto, certifique-se de começar com a equação quadrática na forma padrão,\(a x^{2}+b x+c=0\). Em seguida, fatoramos a expressão à esquerda.
Resolver:\(x^{2}+2 x-8=0\)
- Resposta
-

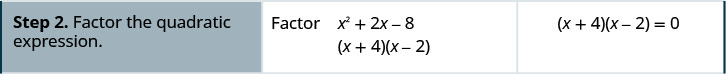



Resolver:\(x^{2}-x-12=0\)
- Resposta
-
\(x=4, x=-3\)
Resolver:\(b^{2}+9 b+14=0\)
- Responda
-
\(b=-2, b=-7\)
- Escreva a equação quadrática na forma padrão,\(a x^{2}+b x+c=0\).
- Fator a expressão quadrática.
- Use a propriedade Zero Product.
- Resolva as equações lineares.
- Verifique.
Antes de fatorar, devemos garantir que a equação quadrática esteja na forma padrão.
Resolver:\(2 y^{2}=13 y+45\)
- Responda
-
\(2 y^{2}=13 y+45\) Escreva a equação quadrática na forma padrão. \(2 y^{2}-13 y-45=0\) Fator a expressão quadrática. \((2 y+5)(y-9)=0\) Use a Propriedade do Produto Zero
para definir cada fator como 0.\(2 y+5=0\) \(y-9=0\) Resolva cada equação. \(y=-\frac{5}{2}\) \(y=9\) Verifique suas respostas. 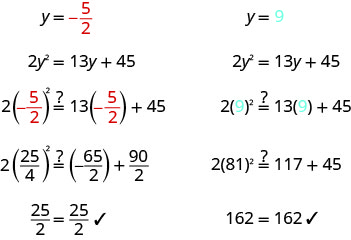
Resolver:\(3 c^{2}=10 c-8\)
- Responda
-
\(c=0, c=\frac{4}{3}\)
Resolver:\(2 d^{2}-5 d=3\)
- Responda
-
\(d=3, d=-\frac{1}{2}\)
Resolver:\(5 x^{2}-13 x=7 x\)
- Responda
-
\(5 x^{2}-13 x=7 x\) Escreva a equação quadrática na forma padrão. \(5 x^{2}-20 x=0\) Fatize o lado esquerdo da equação. \(5 x(x-4)=0\) Use a Propriedade do Produto Zero
para definir cada fator como 0.\(5x=0\) \(x−4=0\) Resolva cada equação. \(x=0\) \(x=4\) Verifique suas respostas. 
Resolver:\(6 a^{2}+9 a=3 a\)
- Responda
-
\(a=0, a=-1\)
Resolver:\(45 b^{2}-2 b=-17 b\)
- Responda
-
\(b=0, b=-\frac{1}{3}\)
Resolver equações quadráticas por fatoração fará uso de todas as técnicas de fatoração que você aprendeu neste capítulo! Você reconhece o padrão especial do produto no próximo exemplo?
Resolver:\(144 q^{2}=25\)
- Responda
-
\(\begin{array}{lrllrl} & 144 q^{2}&=&25 \\ \text { Write the quadratic equation in standard form. }& 144 q^{2}-25&=& 0 \\ \text { Factor. It is a difference of squares. } & (12 q-5)(12 q+5) & = & 0 \\ \text { Use the Zero Product Property to set each factor to } 0 . & 12 q-5&=&0 & 12 q+5&=&0 \\\text { Solve each equation. } & 12 q & = & 5 & 12 q&=&-5 \\ & q&=&\frac{5}{12} & q & =&-\frac{5}{12} \\ \text { Check your answers. }\end{array}\)
Resolver:\(25 p^{2}=49\)
- Responda
-
\(p=\frac{7}{5}, p=-\frac{7}{5}\)
Resolver:\(36 x^{2}=121\)
- Responda
-
\(x=\frac{11}{6}, x=-\frac{11}{6}\)
O lado esquerdo no próximo exemplo é fatorado, mas o lado direito não é zero. Para usar a Propriedade do Produto Zero, um lado da equação deve ser zero. Multiplicaremos os fatores e, em seguida, escreveremos a equação na forma padrão.
Resolver:\((3 x-8)(x-1)=3 x\)
- Responda
-
\(\begin{array}{ll} & (3 x-8)(x-1)=3 x \\ \text { Multiply the binomials. }& 3 x^{2}-11 x+8=3 x \\ \text { Write the quadratic equation in standard form. }& 3 x^{2}-14 x+8=0\\ \text { Factor the trinomial. }& (3 x-2)(x-4)=0\\\text { Use the Zero Product Property to set each factor to } 0 . & 3 x-2=0 \quad x-4=0 \\ \text { Solve each equation. } & 3 x=2 \quad x=4 \\ & x=\frac{2}{3} \\ \text { Check your answers. } & \text {The check is left to you! } \end{array}\)
Resolver:\((2 m+1)(m+3)=12 m\)
- Responda
-
\(m=1, m=\frac{3}{2}\)
Resolver:\((k+1)(k-1)=8\)
- Responda
-
\(k=3, k=-3\)
A Propriedade do Produto Zero também se aplica ao produto de três ou mais fatores. Se o produto for zero, pelo menos um dos fatores deve ser zero. Podemos resolver algumas equações de grau superior a dois usando a Propriedade do Produto Zero, assim como resolvemos equações quadráticas.
Resolver:\(9 m^{3}+100 m=60 m^{2}\)
- Responda
-
\(\begin{array}{lrllrl} & 9 m^{3}+100 m&=&60 m^{2}\\ \text { Bring all the terms to one side so that the other side is zero. } & 9 m^{3}-60 m^{2}+100 m&=&0 \\ \text { Factor the greatest common factor first. } & m\left(9 m^{2}-60 m+100\right)&=&0 \\ \text { Factor the trinomial. } & m(3 m-10)(3 m-10)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & m&=&0 & 3 m-10&=&0 & 3 m-10&=&0 \\ \text { Solve each equation. } & m&=&0 & m&=&\frac{10}{3}& m&=&\frac{10}{3} \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Resolver:\(8 x^{3}=24 x^{2}-18 x\)
- Responda
-
\(x=0, x=\frac{3}{2}\)
Resolver:\(16 y^{2}=32 y^{3}+2 y\)
- Responda
-
\(y=0, y=\frac{1}{4}\)
Quando fatorarmos a equação quadrática no próximo exemplo, obteremos três fatores. No entanto, o primeiro fator é uma constante. Sabemos que esse fator não pode ser igual a 0.
Resolver:\(4 x^{2}=16 x+84\)
- Responda
-
\(\begin{array}{lrllrl} & 4 x^{2}&=&16 x+84\\ \text { Write the quadratic equation in standard form. }& 4 x^{2}-16 x-84&=&0 \\ \text { Factor the greatest common factor first. }& 4\left(x^{2}-4 x-21\right)&=&0 \\ \text { Factor the trinomial. } & 4(x-7)(x+3)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & 4&\neq&0 & x-7&=&0 & x +3&=&0 \\ \text { Solve each equation. } & 4&\neq&0 & x&=&7& x&=&-3 \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Resolver:\(18 a^{2}-30=-33 a\)
- Responda
-
\(a=-\frac{5}{2}, a=\frac{2}{3}\)
Resolver:\(123 b=-6-60 b^{2}\)
- Responda
-
\(b=2, b=\frac{1}{20}\)
Resolva aplicações modeladas por equações quadráticas
A estratégia de resolução de problemas que usamos anteriormente para aplicativos que se traduzem em equações lineares também funcionará bem para aplicativos que se traduzem em equações quadráticas. Vamos copiar a estratégia de resolução de problemas aqui para que possamos usá-la como referência.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Traduza em uma equação. Pode ser útil reafirmar o problema em uma frase com todas as informações importantes. Em seguida, traduza a frase em inglês em uma equação de álgebra.
- Resolva a equação usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
Começaremos com um problema numérico para praticar a tradução de palavras em uma equação quadrática.
O produto de dois números inteiros consecutivos é\(132 .\) Encontre os números inteiros.
- Responda
-
\(\begin{array}{ll} \textbf { Step 1. Read} \text { the problem. } \\ \textbf { Step 2. Identify} \text { what we are looking for. } & \text { We are looking for two consecutive integers. } \\ \textbf { Step 3. Name} \text{ what we are looking for. } & \begin{array}{l}{\text { Let } n=\text { the first integer }} \\ {\space n+1=\text { the next consecutive integer }}\end{array} \\\textbf { Step 4. Translate} \text { into an equation. Restate the } & \text { The product of the two consecutive integers is } 132 . \\ \text { problem in a sentence. } \\ \text { Translate to an equation. } & \begin{array}{c}{\text { The first integer times the next integer is } 132 .} \\ {n(n+1)=132}\end{array} \\ \textbf { Step 5. Solve}\text { the equation. } & n^{2}+n=132 \\ \text { Bring all the terms to one side. } & n^{2}+n-132=0 \\ \text { Factor the trinomial. } & (n-11)(n+12)=0 \\ \text { Use the zero product property. } & n-11=0 \quad n+12=0 \\ \text { Solve the equations. } & n=11 \quad n=-12 \end{array}\)
O produto de dois números inteiros consecutivos é\(240 .\) Encontre os números inteiros.
- Responda
-
\(-15,-16\)e\(15,16\)
O produto de dois números inteiros consecutivos é\(420 .\) Encontre os números inteiros.
- Responda
-
\(-21,-20\)e\(20,21\)
Você ficou surpreso com o par de números inteiros negativos que é uma das soluções para o exemplo anterior? O produto dos dois inteiros positivos e o produto dos dois números inteiros negativos fornecem 132.
Em algumas aplicações, soluções negativas resultarão da álgebra, mas não serão realistas para a situação.
Um jardim retangular tem uma área de 15 pés quadrados. O comprimento do jardim é dois pés a mais do que a largura. Encontre o comprimento e a largura do jardim.
- Responda
-
Etapa 1. Leia o problema. Em problemas envolvendo figuras geométricas, um esboço pode ajudar você a visualizar a situação. 
Etapa 2. Identifique o que você está procurando. Estamos procurando o comprimento e a largura. Etapa 3. Diga o que você está procurando.
O comprimento é dois pés a mais do que a largura.Seja W = a largura do jardim.
W + 2 = o comprimento do jardimEtapa 4. Traduza em uma equação.
Reafirme as informações importantes em uma frase.
A área do jardim retangular é de 15 pés quadrados.Use a fórmula para a área de um retângulo. \(A=L \cdot W\) Substitua as variáveis. \(15=(W+2) W\) Etapa 5. Resolva a equação. Distribua primeiro. \(15=W^{2}+2 W\) Obtenha zero em um lado. \(0=W^{2}+2 W-15\) Considere o trinômio. \(0=(W+5)(W-3)\) Use a propriedade Zero Product. \(0=W+5\) \(0=W−3\) Resolva cada equação. \(−5=W\) \(3=W\) Como W é a largura do jardim, não
faz sentido que seja
negativo. Eliminamos esse valor para W.\(W=−5\) cannot be the width, since it's negative.
\(W=3\)\(3=W\)
A largura é de 3 pés.Encontre o valor do comprimento. \(\text{length}=W+2\) \(\text{length}=3+2\) \(\text{length}=5\) O comprimento é de 5 pés. Etapa 6. Verifique a resposta.
A resposta faz sentido?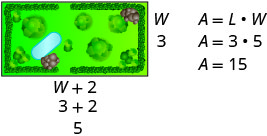
Sim, isso faz sentido. Etapa 7. Responda à pergunta. A largura do jardim é de 3 pés
e o comprimento é de 5 pés.
Uma placa retangular tem uma área de 30 pés quadrados. O comprimento da placa é um pé a mais do que a largura. Encontre o comprimento e a largura da placa.
- Responda
-
55 pés e 66 pés
Um pátio retangular tem uma área de 180 pés quadrados. A largura do pátio é três pés menor que o comprimento. Encontre o comprimento e a largura do pátio.
- Responda
-
12 pés e 15 pés
Em um capítulo anterior, usamos o Teorema de Pitágoras\(\left(a^{2}+b^{2}=c^{2}\right)\). Ele deu a relação entre as pernas e a hipotenusa de um triângulo reto.
Usaremos essa fórmula para no próximo exemplo.
Justine quer colocar um baralho no canto de seu quintal em forma de triângulo reto, conforme mostrado abaixo. A hipotenusa terá 17 pés de comprimento. O comprimento de um lado será 7 pés a menos que o comprimento do outro lado. Encontre os comprimentos das laterais do baralho.
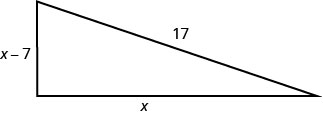
- Responda
-
Etapa 1. Leia o problema. Etapa 2. Identifique o que você está procurando. Estamos procurando os comprimentos das laterais
do convés.Etapa 3. Diga o que você está procurando.
Um lado é 7 a menos que o outro.Seja x = comprimento de um lado do convés
x − 7 = comprimento do outro ladoEtapa 4. Traduza em uma equação.
Como esse é um triângulo reto, podemos usar o Teorema
de Pitágoras.\(a^{2}+b^{2}=c^{2}\) Substitua as variáveis. \(x^{2}+(x-7)^{2}=17^{2}\) Etapa 5. Resolva a equação. \(x^{2}+x^{2}-14 x+49=289\) Simplifique. \(2 x^{2}-14 x+49=289\) É uma equação quadrática, então obtenha zero em um lado. \(2 x^{2}-14 x-240=0\) Considere o maior fator comum. \(2\left(x^{2}-7 x-120\right)=0\) Considere o trinômio. \(2(x-15)(x+8)=0\) Use a propriedade Zero Product. \(2\neq 0\) \(x−15=0\) \(x+8=0\) Resolver. \(2\neq 0\) \(x=15\) \(x=-8\) Como\(x\) é um lado do triângulo, não\(x=−8\)
faz sentido.\(2\neq 0\) \(x=15\) \(\cancel{x=−8}\) Encontre o comprimento do outro lado. Se o comprimento de um lado for \(x=15\) então o comprimento do outro lado é \(x-7\) \(15 - 7 = 8\) 8 é o comprimento do outro lado. Etapa 6. Verifique a resposta.
Esses números fazem sentido?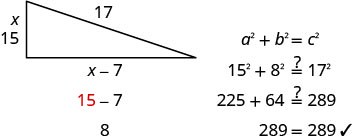
Etapa 7. Responda à pergunta. As laterais do convés são de 8, 15 e 17 pés.
A vela de um barco é um triângulo reto. O comprimento de um lado da vela é 7 pés a mais do que o outro lado. A hipotenusa é 13. Encontre os comprimentos dos dois lados da vela.
- Responda
-
5 pés e 12 pés
Um jardim de meditação tem a forma de um triângulo reto, com uma perna de 7 pés. O comprimento da hipotenusa é um a mais do que o comprimento de uma das outras pernas. Encontre o comprimento da hipotenusa e da outra perna.
- Responda
-
24 pés e 25 pés
Conceitos chave
- Propriedade do produto zero Se\(a \cdot b=0\), então a=0 ou b=0 ou ambos. Veja o exemplo.
- Resolva uma equação quadrática fatorando Para resolver uma equação quadrática fatorando: Veja o exemplo.
- Escreva a equação quadrática na forma padrão,\(a x^{2}+b x+c=0\).
- Fator a expressão quadrática.
- Use a propriedade Zero Product.
- Resolva as equações lineares.
- Verifique.
- Use uma estratégia de resolução de problemas para resolver problemas de palavras. Veja o exemplo.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Traduza em uma equação. Pode ser útil reafirmar o problema em uma frase com todas as informações importantes. Em seguida, traduza a frase em inglês em uma equação de álgebra.
- Resolva a equação usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
Glossário
- equações quadráticas
- são equações nas quais a variável é quadrada.
- Propriedade de produto zero
- A Propriedade do Produto Zero afirma que, se o produto de duas quantidades for zero, pelo menos uma das quantidades será zero.


