7.4: Factor Special Products
- Page ID
- 184156
Ao final desta seção, você poderá:
- Fator trinômios quadrados perfeitos
- Diferenças fatoriais dos quadrados
- Somas fatoriais e diferenças dos cubos
- Escolha o método para fatorar um polinômio completamente
Antes de começar, faça este teste de prontidão.
- Simplifique:\((12 x)^{2}\)
se você perdeu esse problema, revise o Exercício 6.2.22. - Multiplicar:\((m+4)^{2}\)
Se você perdeu esse problema, revise o Exercício 6.4.1. - Multiplicar:\((p-9)^{2}\)
Se você perdeu esse problema, revise o Exercício 6.4.4. - Multiplicar:\((k+3)(k-3)\)
Se você perdeu esse problema, revise o Exercício 6.4.16.
A estratégia de fatoração que desenvolvemos na última seção o guiará ao fatorar a maioria dos binômios, trinômios e polinômios com mais de três termos. Vimos que alguns binômios e trinômios resultam de produtos especiais — quadrando binômios e multiplicando conjugados. Se você aprender a reconhecer esses tipos de polinômios, poderá usar os padrões de produtos especiais para fatorá-los muito mais rapidamente.
Trinômios Quadrados do Fator Perfect
Alguns trinômios são quadrados perfeitos. Eles resultam da multiplicação de um binômio pelo próprio. Você pode quadrar um binômio usando FOIL, mas usar o padrão de Quadrados Binomiais que você viu no capítulo anterior economiza um passo. Vamos revisar o padrão de quadrados binomiais ao quadrado de um binômio usando FOIL.
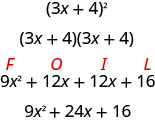
O primeiro termo é o quadrado do primeiro termo do binômio e o último termo é o quadrado do último. O termo médio é o dobro do produto dos dois termos do binômio.
\[\begin{array}{c}{(3 x)^{2}+2(3 x \cdot 4)+4^{2}} \\ {9 x^{2}+24 x+16}\end{array}\]
O trinômio\(9 x^{2}+24+16\) é chamado de trinômio quadrado perfeito. É o quadrado do binômio 3 x +4.
Vamos repetir o padrão de quadrados binomiais aqui para usar como referência na fatoração.
Se a e b forem números reais,
\[(a+b)^{2}=a^{2}+2 a b+b^{2} \qquad(a-b)^{2}=a^{2}-2 a b+b^{2}\]
Quando você coloca um binômio ao quadrado, o produto é um trinômio quadrado perfeito. Neste capítulo, você está aprendendo a fatorar — agora, você começará com um trinômio quadrado perfeito e o incluirá em seus fatores primos.
Você pode fatorar esse trinômio usando os métodos descritos na última seção, pois é da forma\(ax^{2}+bx+c\). Mas se você reconhecer que o primeiro e o último termos são quadrados e o trinômio se encaixa no padrão perfeito de trinômios quadrados, você economizará muito trabalho.
Aqui está o padrão—o inverso do padrão de quadrados binomiais.
Se a e b forem números reais,
\[a^{2}+2 a b+b^{2}=(a+b)^{2} \qquad a^{2}-2 a b+b^{2}=(a-b)^{2}\]
Para fazer uso desse padrão, você precisa reconhecer que um determinado trinômio se encaixa nele. Verifique primeiro se o coeficiente inicial é um quadrado perfeito,\(a^2\). Em seguida, verifique se o último termo é um quadrado perfeito,\(b^2\). Em seguida, verifique o prazo intermediário — é o dobro do produto\(2ab\)? Se tudo estiver certo, você poderá escrever facilmente os fatores.
Fator:\(9 x^{2}+12 x+4\)
- Responda
-



Fator:\(4 x^{2}+12 x+9\)
- Responda
-
\((2 x+3)^{2}\)
Fator:\(9 y^{2}+24 y+16\)
- Responda
-
\((3 y+4)^{2}\)
O sinal do termo intermediário determina qual padrão usaremos. Quando o termo intermediário é negativo, usamos o padrão\(a^{2}-2 a b+b^{2}\), que leva em consideração\((a-b)^{2}\).
As etapas estão resumidas aqui.
\(\begin{array} {lcc} \textbf { Step 1} \text { . Does the trinomial fit the pattern? } & a^{2}+2 a b+b^{2} & a^{2}-2 a b+b^{2} \\ \qquad \bullet \text { Is the first term a perfect square? } & (a)^{2} & (a)^{2} \\ \qquad \quad\text { Write it as a square. } \\ \qquad \bullet \text { Is the last term a perfect square? } & (a)^{2} \qquad\quad (b)^{2} & (a)^{2} \qquad \quad(b)^{2} \\ \qquad \quad \text { Write it as a square. } \\ \qquad \bullet \text { Check the middle term. Is it } 2 a b ? & (a)^{2} \searrow_{2 \cdot a \cdot b }\swarrow(b)^{2} & (a)^{2} \searrow_{2 \cdot a \cdot b} \swarrow(b)^{2} \\ \textbf { Step 2} . \text { Write the square of the binomial. } & (a+b)^{2} & (a-b)^{2} \\ \textbf { Step 3} . \text { Check by multiplying. }\end{array}\)
Vamos trabalhar agora em um em que o termo médio seja negativo.
Fator:\(81 y^{2}-72 y+16\)
- Responda
-
O primeiro e o último termos são quadrados. Veja se o termo intermediário se encaixa no padrão de um trinômio quadrado perfeito. O termo médio é negativo, então o quadrado binomial seria\((a-b)^{2}\).
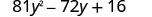
O primeiro e o último termo são quadrados perfeitos? 
Verifique o médio prazo. 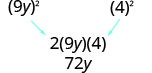
É compatível\((a-b)^{2}\)? Sim. 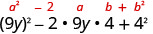
Escreva o quadrado de um binômio. 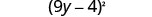
Verifique multiplicando. \((9 y-4)^{2}\) \((9 y)^{2}-2 \cdot 9 y \cdot 4+4^{2}\) \(81 y^{2}-72 y+16 \checkmark\)
Fator:\(64 y^{2}-80 y+25\)
- Responda
-
\((8 y-5)^{2}\)
Fator:\(16 z^{2}-72 z+81\)
- Responda
-
\((4 z-9)^{2}\)
O próximo exemplo será um trinômio quadrado perfeito com duas variáveis.
Fator:\(36 x^{2}+84 x y+49 y^{2}\)
- Responda
-
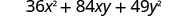
Teste cada termo para verificar o padrão. 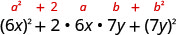
Fator. 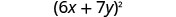
Verifique multiplicando. \((6 x+7 y)^{2}\) \((6 x)^{2}+2 \cdot 6 x \cdot 7 y+(7 y)^{2}\) \(36 x^{2}+84 x y+49 y^{2} \checkmark\)
Fator:\(49 x^{2}+84 x y+36 y^{2}\)
- Responda
-
\((7 x+6 y)^{2}\)
Fator:\(64 m^{2}+112 m n+49 n^{2}\)
- Responda
-
\((8 m+7 n)^{2}\)
Fator:\(9 x^{2}+50 x+25\)
- Responda
-
\(\begin{array}{lc} & 9 x^{2}+50 x+25 \\ \text { Are the first and last terms perfect squares? } & (3 x)^{2} \qquad\quad (5)^2 \\ \text { Check the middle term-is it 2ab? } & (3 x)^{2} \searrow_{2(3 x)(5) }\swarrow (5)^{2}. \\ & \tiny{30x} \\ \text { No! } 30 x \neq 50 x & \text { This does not fit the pattern! } \\ \text { Factor using the "ac" method. } & 9 x^{2}+50 x+25 \\ \begin{array}{c}{\text { ac }} \\ {\text { Notice: } 9 \cdot 25 \text { and } 5 \cdot 45=225} \\ {225}\end{array} \\ {\text { Split the middle term. }} & \begin{array}{c}{9 x^{2}+5 x+45 x+25} \\ {x(9 x+5)+5(9 x+5)} \\ {(9 x+5)(x+5)}\end{array}\\ {\text { Factor by grouping. }} \\ \text { Check. } & \\ \begin{array}{l}{(9 x+5)(x+5)} \\ {9 x^{2}+45 x+5 x+25} \\ {9 x^{2}+50 x+25}\checkmark\end{array}\end{array}\)
Fator:\(16 r^{2}+30 r s+9 s^{2}\)
- Responda
-
\((8 r+3 s)(2 r+3 s)\)
Fator:\(9 u^{2}+87 u+100\)
- Resposta
-
\((3 u+4)(3 u+25)\)
Lembra da primeira etapa em nossa estratégia para fatorar polinômios? Era para perguntar “existe um maior fator comum?” e, se houver, você considera o GCF antes de prosseguir. Trinômios quadrados perfeitos podem ter um GCF em todos os três termos e devem ser considerados primeiro. E, às vezes, uma vez que o GCF tenha sido fatorado, você reconhecerá um trinômio quadrado perfeito.
Fator:\(36 x^{2} y-48 x y+16 y\)
- Resposta
-
\(36 x^{2} y-48 x y+16 y\) Existe um GCF? Sim, 4 anos, então considere. 4\(y\left(9 x^{2}-12 x+4\right)\) Esse é um trinômio quadrado perfeito? Verifique o padrão. 
Fator. 4\(y(3 x-2)^{2}\) Lembre-se: mantenha o fator 4 y no produto final. Confira. \(4y(3 x-2)^{2}\) \(4y[(3 x)^{2}-2 \cdot 3 x \cdot 2+2^{2}]\) \(4 y(9 x)^{2}-12 x+4\) \(36 x^{2} y-48 x y+16 y\checkmark\)
Fator:\(8 x^{2} y-24 x y+18 y\)
- Resposta
-
2\(y(2 x-3)^{2}\)
Fator:\(27 p^{2} q+90 p q+75 q\)
- Resposta
-
3\(q(3 p+5)^{2}\)
Diferenças fatoriais dos quadrados
O outro produto especial que você viu anteriormente foi o padrão Produto dos Conjugados. Você usou isso para multiplicar dois binômios que eram conjugados. Aqui está um exemplo:
\[\begin{array}{c}{(3 x-4)(3 x+4)} \\ {9 x^{2}-16}\end{array}\]
Lembre-se de que, quando você multiplica binômios conjugados, os termos médios do produto são somados a 0. Tudo o que resta é um binômio, a diferença dos quadrados.
Multiplicar conjugados é a única maneira de obter um binômio a partir do produto de dois binômios.
Se a e b forem números reais
\[(a-b)(a+b)=a^{2}-b^{2}\]
O produto é chamado de diferença de quadrados.
Para fatorar, usaremos o padrão do produto “ao contrário” para fatorar a diferença dos quadrados. Uma diferença de fatores quadrados em relação a um produto de conjugados.
Se a e b forem números reais,
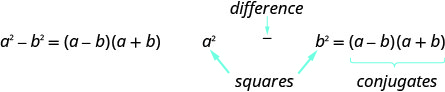
Lembre-se de que “diferença” se refere à subtração. Portanto, para usar esse padrão, você deve se certificar de ter um binômio no qual dois quadrados estão sendo subtraídos.
Fator:\(x^{2}-4\)
- Resposta
-




Fator:\(h^{2}-81\)
- Resposta
-
\((h-9)(h+9)\)
Fator:\(k^{2}-121\)
- Resposta
-
\((k-11)(k+11)\)
\(\begin{array}{lc} \textbf { Step 1} . \text { Does the binomial fit the pattern? } & a^{2}-b^{2} \\ \qquad \bullet \text { Is this a difference? } & \underline{\quad} - \underline{\quad} \\ \qquad \bullet \text { Are the first and last terms perfect squares? } \\ \textbf { Step 2} . \text { Write them as squares. } & (a)^{2}-(b)^{2} \\ \textbf { Step 3.} \text{ Write the product of conjugates. } & (a-b)(a+b) \\ \textbf { Step 4.} \text{ Check by multiplying. } \end{array}\)
É importante lembrar que as somas dos quadrados não são consideradas um produto de binômios. Não há fatores binomiais que se multipliquem para obter a soma dos quadrados. Depois de remover qualquer GCF, a expressão\(a^{2}+b^{2}\) é primordial!
Não se esqueça de que 1 é um quadrado perfeito. Precisaremos usar esse fato no próximo exemplo.
Fator:\(64 y^{2}-1\)
- Resposta
-
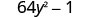
Isso é uma diferença? Sim. 
O primeiro e o último termo são quadrados perfeitos? Sim, escreva-os como quadrados. 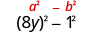
Fator como produto dos conjugados. 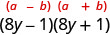
Verifique multiplicando. \((8 y-1)(8 y+1)\) \(64 y^{2}-1 \checkmark\)
Fator:\(m^{2}-1\)
- Resposta
-
\((m-1)(m+1)\)
Fator:\(81 y^{2}-1\)
- Resposta
-
\((9 y-1)(9 y+1)\)
Fator:\(121 x^{2}-49 y^{2}\)
- Resposta
-
\(\begin{array}{lc} & 121 x^{2}-49 y^{2} \\ \text { Is this a difference of squares? Yes. } & (11 x)^{2}-(7 y)^{2} \\ \text { Factor as the product of conjugates. } & (11 x-7 y)(11 x+7 y) \\ \text { Check by multiplying. } & \\ \begin{array}{l}{(11 x-7 y)(11 x+7 y)} \\ {121 x^{2}-49 y^{2}} \checkmark \end{array} \end{array}\)
Fator:\(196 m^{2}-25 n^{2}\)
- Resposta
-
\((16 m-5 n)(16 m+5 n)\)
Fator:\(144 p^{2}-9 q^{2}\)
- Resposta
-
\((12 p-3 q)(12 p+3 q)\)
O binômio no próximo exemplo pode parecer “para trás”, mas ainda é a diferença dos quadrados.
Fator:\(100-h^{2}\)
- Resposta
-
\(\begin{array}{lc} & 100-h^{2} \\ \text { Is this a difference of squares? Yes. } & (10)^{2}-(h)^{2}\\ \text { Factor as the product of conjugates. } & (10-h)(10+h)\\ \text { Check by multiplying. } & \\ \begin{array}{l}{(10-h)(10+h)} \\ {100-h^{2}} \checkmark \end{array} \end{array}\)
Tenha cuidado para não reescrever a expressão original como\(h^{2}-100\).
Considere\(h^{2}-100\) por si mesmo e depois observe como o resultado difere\((10-h)(10+h)\).
Fator:\(144-x^{2}\)
- Resposta
-
\((12-x)(12+x)\)
Fator:\(169-p^{2}\)
- Resposta
-
\((13-p)(13+p)\)
Para fatorar completamente o binômio no próximo exemplo, fatoraremos uma diferença de quadrados duas vezes!
Fator:\(x^{4}-y^{4}\)
- Resposta
-
\(\begin{array}{lc}\text { Is this a difference of squares? Yes. } & {x^{4}-y^{4}} \\\text { Factor it as the product of conjugates. } & {\left(x^{2}\right)^{2}-\left(y^{2}\right)^{2}} \\ \text { Notice the first binomial is also a difference of squares! } & {\left(x^{2}-y^{2}\right)\left(x^{2}+y^{2}\right)} \\ \text { Factor it as the product of conjugates. The last }& {(x-y)(x+y)\left(x^{2}+y^{2}\right)} \\ \text { factor, the sum of squares, cannot be factored. } \\ \\ \text { Check by multiplying. } & \\\begin{array}{l}{(x-y)(x+y)\left(x^{2}+y^{2}\right)} \\ {[(x-y)(x+y)]\left(x^{2}+y^{2}\right)} \\ {\left(x^{2}-y^{2}\right)\left(x^{2}+y^{2}\right)} \\ {x^{4}-y^{4}} \checkmark \end{array} \end{array}\)
Fator:\(a^{4}-b^{4}\)
- Resposta
-
\(\left(a^{2}+b^{2}\right)(a+b)(a-b)\)
Fator:\(x^{4}-16\)
- Resposta
-
\(\left(x^{2}+4\right)(x+2)(x-2)\)
Como sempre, você deve procurar primeiro um fator comum sempre que tiver uma expressão para fatorar. Às vezes, um fator comum pode “disfarçar” a diferença de quadrados e você não reconhecerá os quadrados perfeitos até fatorar o GCF.
Fator:\(8 x^{2} y-98 y\)
- Resposta
-
\(\begin{array}{lc}& 8 x^{2} y-98 y \\ \text { Is there a GCF? Yes, } 2 y-\text { factor it out! } & 2 y\left(4 x^{2}-49\right) \\ \text { Is the binomial a difference of squares? Yes. } & 2 y\left((2 x)^{2}-(7)^{2}\right) \\ \text { Factor as a product of conjugates. } & 2 y(2 x-7)(2 x+7) \\ \text { Check by multiplying. } \\ \\ \begin{array}{l}{2 y(2 x-7)(2 x+7)} \\ {2 y[(2 x-7)(2 x+7)]} \\ {2 y\left(4 x^{2}-49\right)} \\ {8 x^{2} y-98 y} \checkmark \end{array} \end{array}\)
Fator:\(7 x y^{2}-175 x\)
- Resposta
-
7\(x(y-5)(y+5)\)
Fator:\(45 a^{2} b-80 b\)
- Resposta
-
5\(b(3 a-4)(3 a+4)\)
Fator:\(6 x^{2}+96\)
- Resposta
-
\(\begin{array}{lc}&6 x^{2}+96 \\ \text { Is there a GCF? Yes, } 6-\text { factor it out! } & 6\left(x^{2}+16\right) \\ \text { Is the binomial a difference of squares? No, it } & \\ \text { is a sum of squares. Sums of squares do not factor! } & \\ \text { Check by multiplying. } \\ \\ \begin{array}{l}{6\left(x^{2}+16\right)} \\ {6 x^{2}+96 }\checkmark \end{array} \end{array}\)
Fator:\(8 a^{2}+200\)
- Resposta
-
8\(\left(a^{2}+25\right)\)
Fator:\(36 y^{2}+81\)
- Resposta
-
9\(\left(4 y^{2}+9\right)\)
Somas de fatores e diferenças de cubos
Há outro padrão especial para fatoração, um que não usamos quando multiplicamos polinômios. Esse é o padrão para a soma e a diferença dos cubos. Escreveremos essas fórmulas primeiro e depois as verificaremos por multiplicação.
\[\begin{aligned} a^{3}+b^{3} &=(a+b)\left(a^{2}-a b+b^{2}\right) \\ a^{3}-b^{3} &=(a-b)\left(a^{2}+a b+b^{2}\right) \end{aligned}\]
Verificaremos o primeiro padrão e deixaremos o segundo para você.
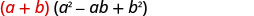 |
|
| Distribuir. |  |
| Multiplique. | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| Combine termos semelhantes. | \(a^{3}+b^{3}\) |
\[\begin{array}{l}{a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)} \\ {a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)}\end{array}\]
Os dois padrões parecem muito parecidos, não é? Mas observe os sinais nos fatores. O sinal do fator binomial corresponde ao sinal do binômio original. E o sinal do termo médio do fator trinomial é o oposto do sinal no binômio original. Se você reconhecer o padrão dos sinais, isso pode ajudá-lo a memorizar os padrões.

O fator trinomial no padrão de soma e diferença de cubos não pode ser fatorado.
Pode ser muito útil aprender a reconhecer os cubos dos números inteiros de 1 a 10, assim como aprendeu a reconhecer os quadrados. Listamos os cubos dos números inteiros de 1 a 10 na Figura\(\PageIndex{1}\).

Fator:\(x^{3}+64\)
- Resposta
-





Fator:\(x^{3}+27\)
- Resposta
-
\((x+3)\left(x^{2}-3 x+9\right)\)
Fator:\(y^{3}+8\)
- Resposta
-
\((y+2)\left(y^{2}-2 y+4\right)\)
Para fatorar a soma ou a diferença dos cubos:
- O binômio se ajusta ao padrão de soma ou diferença de cubos?
- É uma soma ou diferença?
- O primeiro e o último termo são cubos perfeitos?
- Escreva-os como cubos.
- Use o padrão de soma ou diferença de cubos.
- Simplifique dentro dos parênteses
- Verifique multiplicando os fatores.
Fator:\(: x^{3}-1000\)
- Resposta
-

Esse binômio é uma diferença. O primeiro e o último termo são cubos perfeitos. Escreva os termos como cubos. 
Use a diferença do padrão de cubos. 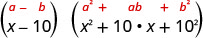
Simplifique. 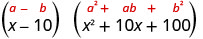
Verifique multiplicando. 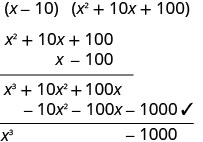
Fator:\(u^{3}-125\)
- Resposta
-
\((u-5)\left(u^{2}+5 u+25\right)\)
Fator:\(v^{3}-343\)
- Resposta
-
\((v-7)\left(v^{2}+7 v+49\right)\)
Tenha o cuidado de usar os sinais corretos nos fatores de soma e diferença dos cubos.
Fator:\(512-125 p^{3}\)
- Resposta
-

Esse binômio é uma diferença. O primeiro e o último termo são cubos perfeitos. Escreva os termos como cubos. 
Use a diferença do padrão de cubos. 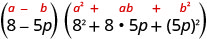
Simplifique. 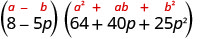
Verifique multiplicando. Vamos deixar o cheque para você.
Fator:\(64-27 x^{3}\)
- Resposta
-
\((4-3 x)\left(16+12 x+9 x^{2}\right)\)
Fator:\(27-8 y^{3}\)
- Resposta
-
\((3-2 y)\left(9+6 y+4 y^{2}\right)\)
Fator:\(27 u^{3}-125 v^{3}\)
- Resposta
-

Esse binômio é uma diferença. O primeiro e o último termo são cubos perfeitos. Escreva os termos como cubos. 
Use a diferença do padrão de cubos. 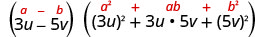
Simplifique. 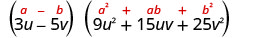
Verifique multiplicando. Vamos deixar o cheque para você.
Fator:\(8 x^{3}-27 y^{3}\)
- Resposta
-
\((2 x-3 y)\left(4 x^{2}+6 x y+9 y^{2}\right)\)
Fator:\(1000 m^{3}-125 n^{3}\)
- Resposta
-
\((10 m-5 n)\left(100 m^{2}+50 m n+25 n^{2}\right)\)
No próximo exemplo, primeiro consideramos o GCF. Então, podemos reconhecer a soma dos cubos.
Fator:\(5 m^{3}+40 n^{3}\)
- Resposta
-
Verifique. Para verificar, talvez seja mais fácil multiplicar primeiro os fatores da soma dos cubos e depois multiplicar esse produto por 5. Vamos deixar a multiplicação para você.
Considere o fator comum. 
Esse binômio é uma soma. O primeiro e o último termo são cubos perfeitos. Escreva os termos como cubos. 
Use o padrão de soma de cubos. 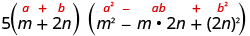
Simplifique. 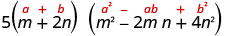
- 5\((m+2 n)\left(m^{2}-2 m n+4 n^{2}\right)\)
Fator:\(500 p^{3}+4 q^{3}\)
- Resposta
-
4\((5 p+q)\left(25 p^{2}-5 p q+q^{2}\right)\)
Fator:\(432 c^{3}+686 d^{3}\)
- Resposta
-
2\((6 c+7 d)\left(36 c^{2}-42 c d+49 d^{2}\right)\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com a fatoração de produtos especiais.
- Soma da diferença dos cubos
- Diferença de fatoração de cubos
Conceitos-chave
- Fator trinômios quadrados perfeitos Veja o exemplo. \(\begin{array} {lcc} \textbf { Step 1} \text { . Does the trinomial fit the pattern? } & a^{2}+2 a b+b^{2} & a^{2}-2 a b+b^{2} \\ \qquad \bullet \text { Is the first term a perfect square? } & (a)^{2} & (a)^{2} \\ \qquad \quad\text { Write it as a square. } \\ \qquad \bullet \text { Is the last term a perfect square? } & (a)^{2} \qquad\quad (b)^{2} & (a)^{2} \qquad \quad(b)^{2} \\ \qquad \quad \text { Write it as a square. } \\ \qquad \bullet \text { Check the middle term. Is it } 2 a b ? & (a)^{2} \searrow_{2 \cdot a \cdot b }\swarrow(b)^{2} & (a)^{2} \searrow_{2 \cdot a \cdot b} \swarrow(b)^{2} \\ \textbf { Step 2} . \text { Write the square of the binomial. } & (a+b)^{2} & (a-b)^{2} \\ \textbf { Step 3} . \text { Check by multiplying. }\end{array}\)
- Diferenças fatoriais dos quadrados Veja o exemplo. \(\begin{array}{lc} \textbf { Step 1} . \text { Does the binomial fit the pattern? } & a^{2}-b^{2} \\ \qquad \bullet \text { Is this a difference? } & \underline{\quad} - \underline{\quad} \\ \qquad \bullet \text { Are the first and last terms perfect squares? } \\ \textbf { Step 2} . \text { Write them as squares. } & (a)^{2}-(b)^{2} \\ \textbf { Step 3.} \text{ Write the product of conjugates. } & (a-b)(a+b) \\ \textbf { Step 4.} \text{ Check by multiplying. } \end{array}\)
- Soma dos fatores e diferença dos cubos Para fatorar a soma ou a diferença dos cubos: Consulte o exemplo.
- O binômio se ajusta ao padrão de soma ou diferença de cubos? É uma soma ou diferença? O primeiro e o último termo são cubos perfeitos?
- Escreva-os como cubos.
- Use o padrão de soma ou diferença de cubos.
- Simplifique dentro dos parênteses
- Verifique multiplicando os fatores.
Glossário
- padrão de trinômios quadrados perfeito
- Se a e b forem números reais,
\[\begin{array}{cc} {a^2+2ab+b^2=(a+b)^2}&{a^2−2ab+b^2=(a−b)^2}\\ \nonumber \end{array}\]
- padrão de diferença de quadrados
- Se a e b forem números reais,

- padrão de soma e diferença de cubos
-
\[\begin{array}{cc} {a^3+b^3=(a+b)(a^2−ab+b^2)}&{a^3−b^3=(a−b)(a^2+ab+b^2)}\\ \nonumber \end{array}\]


