7.3: Trinômios quadráticos fatoriais com coeficiente principal diferente de 1
- Page ID
- 184136
Ao final desta seção, você poderá:
- Reconheça uma estratégia preliminar para fatorar completamente os polinômios
- Trinômios fatoriais da forma\(ax^{2}+bx+c\) com um GCF
- Fatorar trinômios usando tentativa e erro
- Trinômios fatoriais usando o método 'ac'
Antes de começar, faça este teste de prontidão.
- Encontre o GCF de 45\(p^{2}\) e 30\(p^{6}\)
Se você perdeu esse problema, revise o Exercício 7.1.4. - Multiplique\((3 y+4)(2 y+5)\)
Se você perdeu esse problema, revise o Exercício 6.3.37. - Combine termos semelhantes\(12 x^{2}+3 x+5 x+9\)
Se você perdeu esse problema, consulte o Exercício 1.3.37.
Reconheça uma estratégia preliminar para fatorar
Vamos resumir onde estamos até agora com a fatoração de polinômios. Nas duas primeiras seções deste capítulo, usamos três métodos de fatoração: fatorar o GCF, fatorar por agrupamento e fatorar um trinômio “desfazendo” FOIL. Mais métodos seguirão à medida que você continuar neste capítulo, bem como posteriormente em seus estudos de álgebra.
Como você saberá quando usar cada método de fatoração? À medida que você aprende mais métodos de fatoração, como você saberá quando aplicar cada método e não confundi-los? Isso ajudará a organizar os métodos de fatoração em uma estratégia que possa orientá-lo a usar o método correto.
Ao começar a fatorar um polinômio, sempre pergunte primeiro: “Existe o maior fator comum?” Se houver, fatore primeiro.
A próxima coisa a considerar é o tipo de polinômio. Quantos termos ele tem? É um binômio? Um trinômio? Ou tem mais de três termos?
- Se for um trinômio em que o coeficiente principal é um\(x^{2}+b x+c\), use o método “undo FOIL”.
- Se tiver mais de três termos, experimente o método de agrupamento. Esse é o único método a ser usado para polinômios de mais de três termos.
Alguns polinômios não podem ser fatorados. Eles são chamados de “prime”. Abaixo, resumimos os métodos que temos até agora.
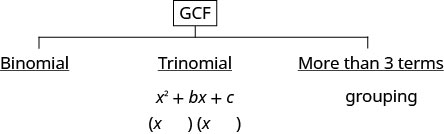
- Existe um fator comum maior?
- Considere isso.
- O polinômio é binomial, trinomial ou há mais de três termos?
- Se for um binômio, no momento não temos nenhum método para fatorá-lo.
- Se for um trinômio da forma\(x^{2}+b x+c\): Undo FOIL\((x\qquad)(x\qquad)\)
- Se tiver mais de três termos: use o método de agrupamento.
- Verifique multiplicando os fatores.
Use a estratégia preliminar para fatorar completamente um polinômio. Um polinômio é fatorado completamente se, exceto monômios, todos os seus fatores forem primos.
Identifique o melhor método a ser usado para fatorar cada polinômio.
- \(6 y^{2}-72\)
- \(r^{2}-10 r-24\)
- \(p^{2}+5 p+p q+5 q\)
- Responda a
-
\[\begin{array}{ll} &6 y^{2}-72\\ \text { Is there a greatest common factor? } & \text {Yes, 6. } \\ \text { Factor out the } 6 &6\left(y^{2}-12\right) \\ \text { Is it a binomial, trinomial, or are there } & \text {Binomial, we have no method to factor } \\ \text { more than } 3 \text { terms? } & \text {binomials yet. } \end{array} \nonumber\]
- Resposta b
-
\[\begin{array}{ll} &r^{2}-10 r-24\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {Trinomial, with leading coefficient } 1, \text { so } \\ \text { more than three terms? }& \text {"undo" FOIL. }\end{array} \nonumber\]
- Resposta c
-
\[\begin{array}{ll} &p^{2}+5 p+p q+5 q\\ \text { Is there a greatest common factor? }& \text {No, there is no common factor. } \\\text { Is it a binomial, trinomial, or are there } &\text {More than three terms, so factor using }\\ \text { more than three terms? }& \text {grouping. }\end{array} \nonumber\]
Identifique o melhor método a ser usado para fatorar cada polinômio:
- \(4 y^{2}+32\)
- \(y^{2}+10 y+21\)
- \(y z+2 y+3 z+6\)
- Responda a
-
nenhum método
- Resposta b
-
desfazer usando FOIL
- Resposta c
-
fatorar com agrupamento
Identifique o melhor método a ser usado para fatorar cada polinômio:
- \(a b+a+4 b+4\)
- \(3 k^{2}+15\)
- \(p^{2}+9 p+8\)
- Responda a
-
fatorar usando agrupamento
- Resposta b
-
nenhum método
- Resposta c
-
desfazer usando FOIL
Fator Trinômios da forma ax 2 + bx + c com um GCF
Agora que organizamos o que abordamos até agora, estamos prontos para fatorar trinômios cujo coeficiente principal não seja 1, trinômios da forma\(a x^{2}+b x+c\). Lembre-se de sempre verificar primeiro se há um GCF! Às vezes, depois de fatorar o GCF, o coeficiente principal do trinômio se torna 1 e você pode fatorá-lo pelos métodos da última seção. Vamos dar alguns exemplos para ver como isso funciona. Fique atento aos sinais nos próximos dois exemplos.
Fator completamente:\(2 n^{2}-8 n-42\).
- Resposta
-
Use a estratégia preliminar.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&2 n^{2}-8 n-42\\ \text { Yes, GCF }=2 . \text { Factor it out. }& 2\left(n^{2}-4 n-21\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 2(n\qquad )(n\qquad) \\ \text { Use } 3 \text { and }-7 \text { as the last terms of the binomials. } & 2(n+3)(n-7) \end{array}\)
Fatores de −21 Soma dos fatores 1 −21 1+ (−21) =−20 3, −7 3+ (−7) =−4* \(\begin{array}{l}{\text {Check. }} \\ {2(n+3)(n-7)} \\ {2\left(n^{2}-7 n+3 n-21\right)} \\ {2\left(n^{2}-4 n-21\right)} \\ {2 n^{2}-8 n-42 }\checkmark \end{array}\)
Fator completamente:\(4 m^{2}-4 m-8\)
- Resposta
-
4\((m+1)(m-2)\)
Fator completamente:\(5 k^{2}-15 k-50\)
- Resposta
-
5\((k+2)(k-5)\)
Fator completamente:\(4 y^{2}-36 y+56\)
- Resposta
-
Use a estratégia preliminar.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&4 y^{2}-36 y+56\\ \text { Yes, GCF }=4 . \text { Factor it out. }&4\left(y^{2}-9 y+14\right) \\\text { Inside the parentheses, is it a binomial, trinomial, or are there }&\\ \text { more than three terms? }& \\ \text { It is a trinomial whose coefficient is } 1, \text { so undo FOIL. } & 4(y\qquad )(y\qquad) \\\text { Use a table like the one below to find two numbers that multiply to }&\\ 14 \text { and add to }-9\\ \text { Both factors of } 14 \text { must be negative. } & 4(y-2)(y-7) \end{array}\)Fatores de 14 Soma dos fatores −1, −14 −1+ (−14) =−15 −2, −7 −2+ (−7) =−9* \(\begin{array}{l}{\text { Check. }} \\ {4(y-2)(y-7)} \\ {4\left(y^{2}-7 y-2 y+14\right)} \\ {4\left(y^{2}-9 y+14\right)} \\ {4 y^{2}-36 y+42 } \checkmark \end{array}\)
Fator completamente:\(3 r^{2}-9 r+6\)
- Resposta
-
3\((r-1)(r-2)\)
Fator completamente:\(2 t^{2}-10 t+12\)
- Resposta
-
2\((t-2)(t-3)\)
No próximo exemplo, o GCF incluirá uma variável.
Fator completamente:\(4 u^{3}+16 u^{2}-20 u\)
- Resposta
-
Use a estratégia preliminar.
\(\begin{array}{ll} \text { Is there a greatest common factor? }&4 u^{3}+16 u^{2}-20 u\\ \text { Yes, GCF }=4 u . \text { Factor it. }&4 u\left(u^{2}+4 u-5\right) \\\text { Binomial, trinomial, or more than three terms? }&\\ \text { more than three terms? }& \\ \text { It is a trinomial. So "undo FOIL." } & 4u(u\qquad )(u\qquad) \\\text { Use a table like the table below to find two numbers that }&4 u(u-1)(u+5)\\ \text { multiply to }-5 \text { and add to } 4\end{array}\)Fatores de −5 Soma dos fatores −1,5 −1+5=4* 1, −5 1+ (−5) =−4 Verifique.
\(\begin{array}{l}{4 u(u-1)(u+5)} \\ {4 u\left(u^{2}+5 u-u-5\right)} \\ {4 u\left(u^{2}+4 u-5\right)} \\ {4 u^{3}+16 u^{2}-20 u }\checkmark \end{array}\)
Fator completamente:\(5 x^{3}+15 x^{2}-20 x\)
- Resposta
-
5\(x(x-1)(x+4)\)
Fator completamente:\(6 y^{3}+18 y^{2}-60 y\)
- Resposta
-
6\(y(y-2)(y+5)\)
Trinômios fatoriais usando tentativa e erro
O que acontece quando o coeficiente principal não é 1 e não há GCF? Existem vários métodos que podem ser usados para fatorar esses trinômios. Primeiro, usaremos o método de tentativa e erro.
Vamos considerar o trinômio\(3 x^{2}+5 x+2\)
Em nosso trabalho anterior, esperamos que isso seja considerado em dois binômios.
\[\begin{array}{c}{3 x^{2}+5 x+2} \\ {( \qquad)( \qquad)}\end{array}\]
Sabemos que os primeiros termos dos fatores binomiais se multiplicarão para nos dar 3\(x^{2}\). Os únicos fatores de 3\(x^{2}\) são\(1 x, 3 x\). Podemos colocá-los nos binômios.
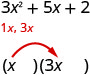
Verifique. Faz\(1 x \cdot 3 x=3 x^{2}\)?
Sabemos que os últimos termos dos binômios se multiplicarão por 2. Como esse trinômio tem todos os termos positivos, precisamos apenas considerar fatores positivos. Os únicos fatores de 2 são 1 e 2. Mas agora temos dois casos a considerar, pois isso fará diferença se escrevermos 1, 2 ou 2, 1.

Quais fatores estão corretos? Para decidir isso, multiplicamos os termos interno e externo.
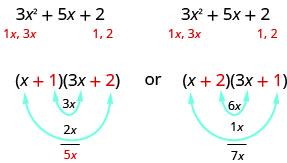
Como o termo médio do trinômio é 5 x, os fatores no primeiro caso funcionarão. Vamos verificar o FOIL.
\[\begin{array}{l}{(x+1)(3 x+2)} \\ {3 x^{2}+2 x+3 x+2} \\ {3 x^{2}+5 x+2}\checkmark \end{array}\]
Nosso resultado da fatoração é:
\[\begin{array}{l}{3 x^{2}+5 x+2} \\ {(x+1)(3 x+2)}\end{array}\]
Fator completamente:\(3 y^{2}+22 y+7\)
- Resposta
-





Fator completamente:\(2 a^{2}+5 a+3\)
- Resposta
-
\((a+1)(2 a+3)\)
Fator completamente:\(4 b^{2}+5 b+1\)
- Resposta
-
\((b+1)(4 b+1)\)
- Escreva o trinômio em ordem decrescente de graus.
- Encontre todos os pares de fatores do primeiro termo.
- Encontre todos os pares de fatores do terceiro termo.
- Teste todas as combinações possíveis dos fatores até que o produto correto seja encontrado.
- Verifique multiplicando.
Quando o termo médio é negativo e o último termo é positivo, os sinais nos binômios devem ser negativos.
Fator completamente:\(6 b^{2}-13 b+5\)
- Resposta
-
Considere todas as combinações de fatores.O trinômio já está em ordem decrescente. 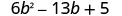
Encontre os fatores do primeiro termo. 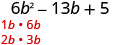
Encontre os fatores do último período. Considere os sinais. Como o último termo, 5 é positivo, seus fatores devem ser positivos ou negativos. O coeficiente do termo médio é negativo, então usamos os fatores negativos. 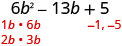
\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 b-1)(3 b-5)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 v}\checkmark \end{array}\end{array}\)\(6 b^{2}-13 b+5\) Fatores possíveis Produto \ (6 b^ {2} -13 b+5\) Fatores possíveis” data-valign="top” class="lt-math-15168"> (b−1) (6b−5) \ (6 b^ {2} -13 b+5\) Produto” data-valign="top” class="lt-math-15168">\(6 b^{2}-11 b+5\) \ (6 b^ {2} -13 b+5\) Fatores possíveis” data-valign="top” class="lt-math-15168"> (b−5) (6b−1) \ (6 b^ {2} -13 b+5\) Produto” data-valign="top” class="lt-math-15168">\(6 b^{2}-31 b+5\) \ (6 b^ {2} -13 b+5\) Fatores possíveis” data-valign="top” class="lt-math-15168"> (2b−1) (3b−5) \ (6 b^ {2} -13 b+5\) Produto” data-valign="top” class="lt-math-15168">\(6 b^{2}-13 b+5\) * \ (6 b^ {2} -13 b+5\) Fatores possíveis” data-valign="top” class="lt-math-15168"> (2b−5) (3b−1) \ (6 b^ {2} -13 b+5\) Produto” data-valign="top” class="lt-math-15168">\(6 b^{2}-17 b+5\)
Fator completamente:\(8 x^{2}-14 x+3\)
- Resposta
-
\((2 x-3)(4 x-1)\)
Fator completamente:\(10 y^{2}-37 y+7\)
- Resposta
-
\((2 y-7)(5 y-1)\)
Quando consideramos uma expressão, sempre procuramos primeiro o maior fator comum. Se a expressão não tiver o maior fator comum, também não pode haver um em seus fatores. Isso pode nos ajudar a eliminar algumas das combinações possíveis de fatores.
Fator completamente:\(14 x^{2}-47 x-7\)
- Resposta
-
Considere todas as combinações de fatores. Usamos cada par de fatores de 14\(x^{2}\) com cada par de fatores de −7.O trinômio já está em ordem decrescente. 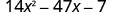
Encontre os fatores do primeiro termo. 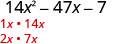
Encontre os fatores do último período. Considere os sinais. Como é negativo, um fator deve ser positivo e outro negativo. 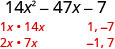
Fatores de\(14x^2\) Emparelhe com Fatores de −7 \ (14x^2\)” data-valign="top” class="lt-math-15168">\(x, 14 x\) 11, −7
−7, 11
(ordem inversa)\ (14x^2\)” data-valign="top” class="lt-math-15168">\(x, 14 x\) −1, 77
77, −1
(ordem inversa)\ (14x^2\)” data-valign="top” class="lt-math-15168">\(2x,7x\) 11, −7
−7, 11
(ordem inversa)\ (14x^2\)” data-valign="top” class="lt-math-15168">\(2x,7x\) −1, 77
77, −1
(ordem inversa)Esses pares levam às seguintes oito combinações.
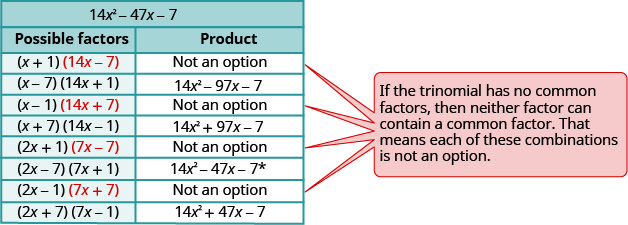
\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 x-7)(7 x+1)\\\\\text {Check by multiplying. } \\\\\begin{array}{l}{(2 b-1)(3 b-5)} \\ {6 b^{2}-10 b-3 b+5} \\ {6 b^{2}-13 b+5 }\checkmark \end{array}\end{array}\)
Fator completamente:\(8 a^{2}-3 a-5\)
- Resposta
-
\((a-1)(8 a+5)\)
Fator completamente:\(6 b^{2}-b-15\)
- Resposta
-
\((2 b+3)(3 b-5)\)
Fator completamente:\(18 n^{2}-37 n+15\)
- Resposta
-
O trinômio já está em ordem decrescente. \(18 n^{2}-37 n+15\) Encontre os fatores do primeiro termo. 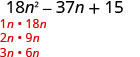
Encontre os fatores do último período. Considere os sinais. Como 15 é positivo e o coeficiente do médio prazo é negativo, usamos os fatores negativos. 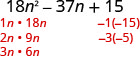
Considere todas as combinações de fatores.

\(\begin{array}{ll}\text{The correct factors are those whose product} & \\ \text{is the original trinomial.} & (2 n-3)(9 n-5)\\\\\text {Check by multiplying. } \\\\ \begin{array}{l}{(2 n-3)(9 n-5)} \\ {18 n^{2}-10 n-27 n+15} \\ {18 n^{2}-37 n+15 } \checkmark\end{array} \end{array}\)
Fator completamente:\(18 x^{2}-3 x-10\)
- Resposta
-
\((3 x+2)(6 x-5)\)
Fator completamente:\(30 y^{2}-53 y-21\)
- Resposta
-
\((3 y+1)(10 y-21)\)
Não se esqueça de procurar primeiro um GCF.
Fator completamente:\(10 y^{4}+55 y^{3}+60 y^{2}\)
- Resposta
-
\(10 y^{4}+55 y^{3}+60 y^{2}\) Observe o maior fator comum e fatore-o primeiro. 5\(y^{2}\left(2 y^{2}+11 y+12\right)\) Considere o trinômio. 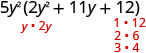
Considere todas as combinações.
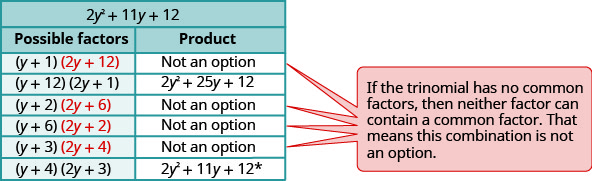
\(\begin{array}{ll}\text{The correct factors are those whose product} &5 y^{2}(y+4)(2 y+3) \\ \text{is the original trinomial. Remember to include} & \\\text {the factor } 5 y^{2}\\\text {Check by multiplying. } \\\\ \begin{array}{l}{5 y^{2}(y+4)(2 y+3)} \\ {5 y^{2}\left(2 y^{2}+8 y+3 y+12\right)} \\ {10 y^{4}+55 y^{3}+60 y^{2}}\checkmark\end{array} \end{array}\)
Fator completamente:\(15 n^{3}-85 n^{2}+100 n\)
- Resposta
-
5\(n(n-4)(3 n-5)\)
Fator completamente:\(56 q^{3}+320 q^{2}-96 q\)
- Resposta
-
8\(q(q+6)(7 q-2)\)
Trinômios fatoriais usando o método “ac”
Outra forma de fatorar os trinômios da forma\(ax^2+bx+c\) é o método “ac”. (O método “ac” às vezes é chamado de método de agrupamento.) O método “ac” é, na verdade, uma extensão dos métodos que você usou na última seção para fatorar trinômios com o coeficiente inicial um. Esse método é muito estruturado (passo a passo) e sempre funciona!
Fator:\(6 x^{2}+7 x+2\)
- Resposta
-


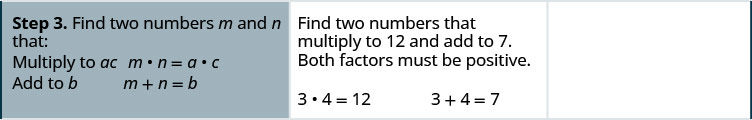



Fator:\(6 x^{2}+13 x+2\)
- Resposta
-
\((x+2)(6 x+1)\)
Fator:\(4 y^{2}+8 y+3\)
- Resposta
-
\((2 y+1)(2 y+3)\)
- Fator qualquer GCF.
- Encontre o produto ac.
- Encontre dois números m e n que:
\(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\) - Divida o termo intermediário usando m e n:
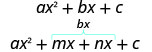
- Fator por agrupamento.
- Verifique multiplicando os fatores.
Quando o terceiro termo do trinômio for negativo, os fatores do terceiro termo terão sinais opostos.
Fator:\(8 u^{2}-17 u-21\)
- Resposta
-
Existe um fator comum maior? Não. 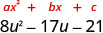
Encontre\(a\cdot c\) \(a\cdot c\) 8 (−21) −168 Encontre dois números que se multiplicam até −168 e somem a −17. O fator maior deve ser negativo.
Fatores de −168 Soma dos fatores 1 −168 1+ (−168) =−167 2, −84 2+ (−84) =−82 3, −56 3+ (−56) =−53 4,2 −42 4+ (−42) =−38 6, −28 6+ (−28) =−22 7, −24 7+ (−24) =−17* 8, −21 8+ (−21) =−13 \(\begin{array}{lc}\text { Split the middle term using } 7 u \text { and }-24 u &8 u^{2}-17 u-21 \\ & \qquad\space \swarrow\searrow \\ & \underbrace{8 u^{2}+7 u} \underbrace{-24 u-21} \\ \text { Factor by grouping. } & u(8 u+7)-3(8 u+7) \\ & (8 u+7)(u-3) \\ \text { Check by multiplying. } & \begin{array}{l}{(8 u+7)(u-3)} \\ {8 u^{2}-24 u+7 u-21} \\ {8 u^{2}-17 u-21} \checkmark \end{array} \end{array}\)
Fator:\(20 h^{2}+13 h-15\)
- Resposta
-
\((4 h-5)(5 h+3)\)
Fator:\(6 g^{2}+19 g-20\)
- Resposta
-
\((q+4)(6 q-5)\)
Fator:\(2 x^{2}+6 x+5\)
- Resposta
-
Existe um fator comum maior? Não. 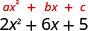
Encontre um ⋅c a⋅c 2 (5) 10 Encontre dois números que se multiplicam por 10 e somem a 6.
Fatores de 10 Soma dos fatores 1,10 1+10 = 11 2, 5 2+5=7 Não há fatores que se multipliquem para 10 e se somam a 6. O polinômio é primo.
Fator:\(10 t^{2}+19 t-15\)
- Resposta
-
\((2 t+5)(5 t-3)\)
Fator:\(3 u^{2}+8 u+5\)
- Resposta
-
\((u+1)(3 u+5)\)
Não se esqueça de procurar um fator comum!
Fator:\(10 y^{2}-55 y+70\)
- Resposta
-
Existe um fator comum maior? Sim. O GCF é 5. 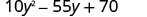
Fator isso. Tenha o cuidado de manter o fator 5 em toda a solução! 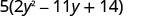
O trinômio dentro dos parênteses tem um coeficiente principal que não é 1. 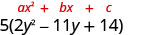
Considere o trinômio. 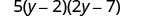
Verifique multiplicando todos os três fatores. 5\(\left(2 y^{2}-2 y-4 y+14\right)\) 5\(\left(2 y^{2}-11 y+14\right)\) \(10 y^{2}-55 y+70\)✓
Fator:\(16 x^{2}-32 x+12\)
- Resposta
-
4\((2 x-3)(2 x-1)\)
Fator:\(18 w^{2}-39 w+18\)
- Resposta
-
3\((3 w-2)(2 w-3)\)
Agora podemos atualizar a Estratégia de Fatoração Preliminar, conforme mostrado na Figura\(\PageIndex{1}\) e detalhada em Escolha uma estratégia para fatorar polinômios completamente (atualizada), para incluir trinômios do formulário\(a x^{2}+b x+c\). Lembre-se de que alguns polinômios são primos e, portanto, não podem ser fatorados.

- Existe um fator comum maior?
- Fator isso.
- O polinômio é binomial, trinomial ou há mais de três termos?
- Se for um binômio, no momento não temos nenhum método para fatorá-lo.
- Se for um trinômio da forma\(x^{2}+b x+c\)
Undo FOIL\\((x\qquad)(x\qquad)\). - Se for um trinômio da forma\(a x^{2}+b x+c\)
Use Tentativa e Erro ou o método “ac”. - Se tiver mais de três termos,
use o método de agrupamento.
- Verifique multiplicando os fatores.
Acesse esses recursos on-line para obter instruções e práticas adicionais com os trinômios de fatoração do formulário\(a x^{2}+b x+c\)
Conceitos-chave
- Trinômios fatoriais do formulário\(a x^{2}+b x+c\) usando tentativa e erro: veja o exemplo.
- Escreva o trinômio em ordem decrescente de graus.
- Encontre todos os pares de fatores do primeiro termo.
- Encontre todos os pares de fatores do terceiro termo.
- Teste todas as combinações possíveis dos fatores até que o produto correto seja encontrado.
- Verifique multiplicando.
- Trinômios fatoriais da forma\(a x^{2}+b x+c\) usando o método “ac”: veja o exemplo.
- Fator qualquer GCF.
- Encontre o produto ac.
- Encontre dois números m e n que:\(\begin{array}{ll}{\text { Multiply to } a c} & {m \cdot n=a \cdot c} \\ {\text { Add to } b} & {m+n=b}\end{array}\)
- Divida o termo intermediário usando m e n:
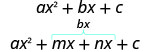
- Fator por agrupamento.
- Verifique multiplicando os fatores.
- Escolha uma estratégia para fatorar completamente os polinômios (atualizada):
- Existe um fator comum maior? Fator isso.
- O polinômio é binomial, trinomial ou há mais de três termos?
Se for um binômio, no momento não temos nenhum método para fatorá-lo.
Se for um trinômio da forma\(x^2+bx+c\)
Undo FOIL\((x\qquad)(x\qquad)\).
Se for um trinômio da forma\(ax^2+bx+c\)
Use Tentativa e Erro ou o método “ac”.
Se tiver mais de três termos,
use o método de agrupamento. - Verifique multiplicando os fatores.
Glossário
- polinômios primos
- Polinômios que não podem ser fatorados são polinômios primos.


