6.2: Use propriedades de multiplicação de expoentes
- Page ID
- 184376
Ao final desta seção, você poderá:
- Simplifique expressões com expoentes
- Simplifique as expressões usando a propriedade Product para expoentes
- Simplifique expressões usando a propriedade de potência para expoentes
- Simplifique expressões usando o produto para uma propriedade de energia
- Simplifique as expressões aplicando várias propriedades
- Multiplique monômios
Antes de começar, faça este teste de prontidão.
- Simplifique:\(\frac{3}{4}\cdot \frac{3}{4}\)
se você perdeu esse problema, revise o Exercício 1.6.13. - Simplifique:\((−2)(−2)(−2)\).
Se você perdeu esse problema, revise o Exercício 1.5.13.
Simplifique expressões com expoentes
Lembre-se de que um expoente indica multiplicação repetida da mesma quantidade. Por exemplo,\(2^4\) significa o produto de\(4\) fatores de\(2\), então\(2^4\) significa\(2·2·2·2\).
Vamos revisar o vocabulário para expressões com expoentes.
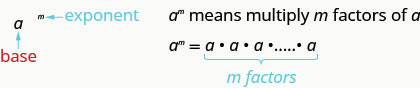
Isso é lido\(a\) ao\(m^{th}\) poder.
Na expressão\(a^{m}\), o expoente nos\(m\) diz quantas vezes usamos a base a como fator.

Antes de começarmos a trabalhar com expressões variáveis contendo expoentes, vamos simplificar algumas expressões que envolvem somente números.
Simplifique:
- \(4^{3}\)
- \(7^{1}\)
- \(\left(\frac{5}{6}\right)^{2}\)
- \((0.63)^{2}\)
- Resposta
-
- \(\begin{array}{ll} & 4^{3}\\ {\text { Multiply three factors of } 4 .} & {4 \cdot 4 \cdot 4} \\ {\text { Simplify. }} & {64}\end{array}\)
- \(\begin{array}{ll} & 7^{1}\\ \text{Multiply one factor of 7.} & 7\end{array}\)
- \(\begin{array}{ll} &\left(\frac{5}{6}\right)^{2}\\ {\text { Multiply two factors. }} & {\left(\frac{5}{6}\right)\left(\frac{5}{6}\right)} \\ {\text { Simplify. }} & {\frac{25}{36}}\end{array}\)
- \(\begin{array}{ll} &(0.63)^{2}\\ {\text { Multiply two factors. }} & {(0.63)(0.63)} \\ {\text { Simplify. }} & {0.3969}\end{array}\)
Simplifique:
- \(6^{3}\)
- \(15^{1}\)
- \(\left(\frac{3}{7}\right)^{2}\)
- \((0.43)^{2}\)
- Resposta
-
- 216
- 15
- \(\frac{9}{49}\)
- 0,1849
Simplifique:
- \(2^{5}\)
- \(21^{1}\)
- \(\left(\frac{2}{5}\right)^{3}\)
- \((0.218)^{2}\)
- Resposta
-
- 32
- 21
- \(\frac{8}{125}\)
- 0,047524
Simplifique:
- \((-5)^{4}\)
- \(-5^{4}\)
- Resposta
-
- \(\begin{array}{ll} &(-5)^{4}\\{\text { Multiply four factors of }-5} & {(-5)(-5)(-5)} \\ {\text { Simplify. }} & {625}\end{array}\)
- \(\begin{array}{ll} &-5^{4}\\{\text { Multiply four factors of } 5 .} & {-(5 \cdot 5 \cdot 5 \cdot 5)} \\ {\text { Simplify. }} & {-625}\end{array}\)
Observe as semelhanças e diferenças na\(\PageIndex{4}\) parte 1 do exemplo e na\(\PageIndex{4}\) parte 2 do exemplo! Por que as respostas são diferentes? À medida que seguimos a ordem das operações na parte 1, os parênteses nos dizem para elevar o\((−5)\) à 4ª potência. Na parte 2, aumentamos apenas a\(5\) para a 4ª potência e depois pegamos o oposto.
Simplifique:
- \((-3)^{4}\)
- \(-3^{4}\)
- Resposta
-
- 81
- −81
Simplifique:
- \((-13)^{4}\)
- \(-13^{4}\)
- Resposta
-
- 169
- −169
Simplifique as expressões usando a propriedade Product para expoentes
Você viu que, ao combinar termos semelhantes somando e subtraindo, você precisa ter a mesma base com o mesmo expoente. Mas quando você multiplica e divide, os expoentes podem ser diferentes e, às vezes, as bases também podem ser diferentes.
Derivaremos as propriedades dos expoentes procurando padrões em vários exemplos.
Primeiro, veremos um exemplo que leva à propriedade do produto.
 |
|
| O que isso significa? Quantos fatores no total? |
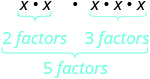 |
| Então, nós temos | 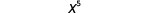 |
| Observe que 5 é a soma dos expoentes, 2 e 3. | 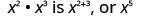 |
Nós escrevemos:\[\begin{array}{c}{x^{2} \cdot x^{3}} \\ {x^{2+3}} \\ {x^{5}}\end{array}\]
A base permaneceu a mesma e adicionamos os expoentes. Isso leva à propriedade do produto para os expoentes.
Se\(a\) for um número real e\(m\) e\(n\) estiverem contando números, então
\[a^{m} \cdot a^{n}=a^{m+n}\]
Para multiplicar com bases semelhantes, adicione os expoentes.
Um exemplo com números ajuda a verificar essa propriedade.
\[\begin{array}{rll} {2^3\cdot2^2} &\stackrel{?}{=} & 2^{2+3}\\ {4\cdot 8} &\stackrel{?}{=} & 2^{5} \\ {32} &=& 32\checkmark\end{array}\]
Simplifique:\(y^{5} \cdot y^{6}\)
- Resposta
-
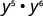
Use a propriedade do produto,\(a^{m} \cdot a^{n}=a^{m+n}\). 
Simplifique. 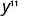
Simplifique:\(b^{9} \cdot b^{8}\)
- Resposta
-
\(b^{17}\)
Simplifique:\(x^{12} \cdot x^{4}\)
- Resposta
-
\(x^{16}\)
Simplifique:
- \(2^{5} \cdot 2^{9}\)
- \(3\cdot 3^{4}\)
- Resposta
-
uma.

Use a propriedade do produto,\(a^{m} \cdot a^{n}=a^{m+n}\). 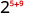
Simplifique. 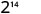
b.
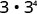
Use a propriedade do produto,\(a^{m} \cdot a^{n}=a^{m+n}\). 
Simplifique. 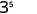
Simplifique:
- \(5\cdot 5^{5}\)
- \(4^{9} \cdot 4^{9}\)
- Resposta
-
- \(5^{6}\)
- \(4^{18}\)
Simplifique:
- \(7^{6} \cdot 7^{8}\)
- \(10 \cdot 10^{10}\)
- Resposta
-
- \(7^{14}\)
- \(10^{11}\)
Simplifique:
- \(a^{7} \cdot a\)
- \(x^{27} \cdot x^{13}\)
- Resposta
-
uma.
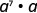
Reescrever,\(a = a^1\) 
Use a propriedade do produto,\(a^m\cdot a^n = a^{m+n}\). 
Simplifique. 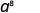
b.

Observe que as bases são as mesmas, então adicione os expoentes. 
Simplifique. 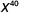
Simplifique:
- \(p^{5} \cdot p\)
- \(y^{14} \cdot y^{29}\)
- Resposta
-
- \(p^{6}\)
- \(y^{43}\)
Simplifique:
- \(z \cdot z^{7}\)
- \(b^{15} \cdot b^{34}\)
- Resposta
-
- \(z^{8}\)
- \(b^{49}\)
Podemos estender a propriedade do produto para expoentes para mais de dois fatores.
Simplifique:\(d^{4} \cdot d^{5} \cdot d^{2}\)
- Resposta
-
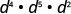
Adicione os expoentes, já que as bases são as mesmas. 
Simplifique. 
Simplifique:\(x^{6} \cdot x^{4} \cdot x^{8}\)
- Resposta
-
\(x^{18}\)
Simplifique:\(b^{5} \cdot b^{9} \cdot b^{5}\)
- Resposta
-
\(b^{19}\)
Simplifique as expressões usando a propriedade de potência para expoentes
Agora vamos ver uma expressão exponencial que contém uma potência elevada a uma potência. Veja se você consegue descobrir uma propriedade geral.
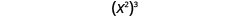 |
|
| O que isso significa? Quantos fatores no total? |
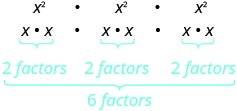 |
| Então nós temos | 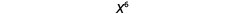 |
| Observe que 6 é o produto dos expoentes, 2 e 3. | 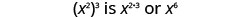 |
Nós escrevemos:
\[\begin{array}{c}{\left(x^{2}\right)^{3}} \\ {x^{2 \cdot 3}} \\ {x^{6}}\end{array}\]
Multiplicamos os expoentes. Isso leva à propriedade de poder dos expoentes.
Se\(a\) for um número real e\(m\) e\(n\) forem números inteiros, então
\[\left(a^{m}\right)^{n}=a^{m \cdot n}\]
Para elevar uma potência a uma potência, multiplique os expoentes.
Um exemplo com números ajuda a verificar essa propriedade.
\[\begin{array} {lll} \left(3^{2}\right)^{3} &\stackrel{?}{=}&3^{2 \cdot 3} \\(9)^{3} &\stackrel{?}{=} & 3^{6} \\ 729 &=&729\checkmark \end{array}\]
Simplifique:
- \(\left(y^{5}\right)^{9}\)
- \(\left(4^{4}\right)^{7}\)
- Resposta
-
uma.
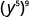
Use a propriedade power,\(\big(a^m\big)^n = a^{m\cdot n}\). 
Simplifique. 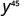
b.
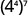
Use a propriedade power. 
Simplifique. 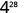
Simplifique:
- \( \left(b^{7}\right)^{5} \)
- \(\left(5^{4}\right)^{3}\)
- Resposta
-
- \( b^{35}\)
- \(5^{12}\)
Simplifique:
- \(\left(z^{6}\right)^{9}\)
- \(\left(3^{7}\right)^{7}\)
- Resposta
-
- \(z^{54}\)
- \(3^{49}\)
Simplifique expressões usando o produto para uma propriedade de energia
Agora veremos uma expressão contendo um produto que é elevado a uma potência. Você consegue encontrar esse padrão?
\(\begin{array}{ll}{\text { What does this mean? }} & {\text { (2x) }^{3}} \\ {\text { We group the like factors together. }} & {2 x \cdot 2 x \cdot 2 x} \\ {\text { How many factors of } 2 \text { and of } x ?} & {2 \cdot 2 \cdot x^{3}} \\ {\text { Notice that each factor was raised to the power and }(2 x)^{3} \text { is } 2^{3} \cdot x^{3}}\end{array}\)
\(\begin{array}{ll}\text{We write:} & {(2 x)^{3}} \\ & {2^{3} \cdot x^{3}}\end{array}\)
O expoente se aplica a cada um dos fatores! Isso leva o produto a uma propriedade de poder para os expoentes.
Se\(a\) e\(b\) forem números reais e\(m\) for um número inteiro, então
\[(a b)^{m}=a^{m} b^{m}\]
Para elevar um produto a uma potência, eleve cada fator a essa potência.
Um exemplo com números ajuda a verificar essa propriedade:
\ [\ begin {array} {lll} (2\ cdot 3) ^ {2} &\ stackrel {?} {=} &2^ {2}\ cdot 3^ {2}\\ 6^ {2} &\ stackrel {?} {=} &4\ cdot 9\\ 36 &=&36
\ marca de verificação\ end {matriz}\]
Simplifique:
- \((-9 d)^{2}\)
- \((3mn)^{3}\).
- Resposta
-
uma.
b.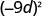
Use o poder de uma propriedade de produto,\((ab)^m=a^m b^m\). 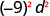
Simplifique. 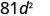
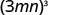
Use o poder de uma propriedade de produto,\((ab)^m=a^m b^m\). 
Simplifique. 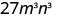
Simplifique:
- \((-12 y)^{2}\)
- \((2 w x)^{5}\)
- Resposta
-
- \(144y^{2}\)
- \(32w^{5} x^{5}\)
Simplifique:
- \((5 w x)^{3}\)
- \((-3 y)^{3}\)
- Resposta
-
- 125\(w^{3} x^{3}\)
- \(-27 y^{3}\)
Simplifique as expressões aplicando várias propriedades
Agora temos três propriedades para multiplicar expressões com expoentes. Vamos resumi-los e, em seguida, faremos alguns exemplos que usam mais de uma das propriedades.
Se\(a\) e\(b\) forem números reais e\(m\) e\(n\) forem números inteiros, então
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]
Todas as propriedades do expoente são verdadeiras para quaisquer números reais\(m\)\(n\) e. No momento, usamos apenas expoentes de números inteiros.
Simplifique:
- \(\left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\)
- \(\left(-6 x^{4} y^{5}\right)^{2}\)
- Resposta
-
- \(\begin{array}{ll}& \left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\\ {\text { Use the Power Property. }}& y^{18} \cdot y^{20} \\ {\text { Add the exponents. }} & y^{38} \end{array}\)
- \(\begin{array}{ll}& \left(-6 x^{4} y^{5}\right)^{2}\\ {\text { Use the Product to a Power Property. }} & {(-6)^{2}\left(x^{4}\right)^{2}\left(y^{5}\right)^{2}} \\ {\text { Use the Power Property. }} & {(-6)^{2}\left(x^{8}\right)\left(y^{10}\right)^{2}} \\ {\text { Simplify. }} & {36 x^{8} y^{10}}\end{array}\)
Simplifique:
- \(\left(a^{4}\right)^{5}\left(a^{7}\right)^{4}\)
- \(\left(-2 c^{4} d^{2}\right)^{3}\)
- Responda
-
- \(a^{48}\)
- \(-8 c^{12} d^{6}\)
Simplifique:
- \(\left(-3 x^{6} y^{7}\right)^{4}\)
- \(\left(q^{4}\right)^{5}\left(q^{3}\right)^{3}\)
- Responda
-
- 81\(x^{24} y^{28}\)
- \(q^{29}\)
Simplifique:
- \((5 m)^{2}\left(3 m^{3}\right)\)
- \(\left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3}\)
- Responda
-
- \(\begin{array}{ll}& (5 m)^{2}\left(3 m^{3}\right)\\{\text { Raise } 5 m \text { to the second power. }} & {5^{2} m^{2} \cdot 3 m^{3}} \\ {\text { Simplify. }} & {25 m^{2} \cdot 3 m^{3}} \\ {\text { Use the Commutative Property. }} & {25 \cdot 3 \cdot m^{2} \cdot m^{3}} \\ {\text { Multiply the constants and add the exponents. }} & {75 m^{5}}\end{array}\)
- \(\begin{array}{ll} & \left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3} \\ \text{Use the Product to a Power Property.} & \left(3^{4} x^{8} y^{4}\right)\left(2^{3} x^{3} y^{6}\right)\\\text{Simplify.} & \left(81 x^{8} y^{4}\right)\left(8 x^{3} y^{6}\right)\\ \text{Use the Commutative Property.} &81\cdot 8 \cdot x^{8} \cdot x^{3} \cdot y^{4} \cdot y^{6} \\\text{Multiply the constants and add the exponents.} & 648x^{11} y^{10}\\ \end{array}\)
Simplifique:
- \((5 n)^{2}\left(3 n^{10}\right)\)
- \(\left(c^{4} d^{2}\right)^{5}\left(3 c d^{5}\right)^{4}\)
- Responda
-
- 75\(n^{12}\)
- 81\(c^{24} d^{30}\)
Simplifique:
- \(\left(a^{3} b^{2}\right)^{6}\left(4 a b^{3}\right)^{4}\)
- \((2 x)^{3}\left(5 x^{7}\right)\)
- Responda
-
- 256\(a^{22} b^{24}\)
- 40\(x^{10}\)
Multiplique monômios
Como um monômio é uma expressão algébrica, podemos usar as propriedades dos expoentes para multiplicar monômios.
Multiplique:\(\left(3 x^{2}\right)\left(-4 x^{3}\right)\)
- Responda
-
\ (\ begin {array} {ll} &\ left (3 x^ {2}\ right)\ left (-4 x^ {3}\ right)\\ text {Use a propriedade comutativa para reorganizar os termos.} & 3\ cdot (-4)\ cdot x^ {2}\ cdot x^ {3}\\
\ text {Multiplicar.} & -12 x^ {5}\ end {matriz}\)
Multiplique:\(\left(5 y^{7}\right)\left(-7 y^{4}\right)\)
- Responda
-
\(-35 y^{11}\)
Multiplique:\(\left(-6 b^{4}\right)\left(-9 b^{5}\right)\)
- Responda
-
54\(b^{9}\)
Multiplique:\(\left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\)
- Responda
-
\(\begin{array}{ll} & \left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\\ \text{Use the Commutative Property to rearrange the terms.} & \frac{5}{6} \cdot 12 \cdot x^{3} \cdot x \cdot y \cdot y^{2}\\ \text{Multiply.} &10x^{4} y^{3}\end{array}\)
Multiplique:\(\left(\frac{2}{5} a^{4} b^{3}\right)\left(15 a b^{3}\right)\)
- Responda
-
6\(a^{5} b^{6}\)
Multiplique:\(\left(\frac{2}{3} r^{5} s\right)\left(12 r^{6} s^{7}\right)\)
- Responda
-
8\(r^{11} s^{8}\)
Acesse esses recursos on-line para obter instruções adicionais e praticar o uso de propriedades de multiplicação de expoentes:
- Propriedades de multiplicação de expoentes
Conceitos-chave
- Notação exponencial
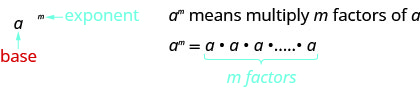
- Propriedades dos expoentes
- Se\(a\) e\(b\) forem números reais e\(m\) e\(n\) forem números inteiros, então
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]


