Skip to main content
Global

5.4: Resolva aplicações com sistemas de equações

  1. Last updated
  2. Save as PDF
  • Page ID
    184081

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Traduza para um sistema de equações
    • Resolva aplicativos de tradução direta
    • Resolva aplicações de geometria
    • Resolva aplicações de movimento uniforme
    Nota

    Antes de começar, faça este teste de prontidão.

    1. A soma de duas vezes um número e nove é 31. Encontre o número.
      Se você perdeu esse problema, revise o Exercício 3.1.10.
    2. Os gêmeos Jon e Ron juntos ganharam $96.000 no ano passado. Ron ganhou $8.000 a mais do que três vezes o que Jon ganhou. Quanto cada um dos gêmeos ganhou?
      Se você perdeu esse problema, revise o Exercício 3.1.31.
    3. Alessio anda de bicicleta\(3\frac{1}{2}\) por horas a uma taxa de 10 milhas por hora. Até onde ele viajou?
      Se você perdeu esse problema, revise o Exercício 2.6.1.

    Anteriormente, neste capítulo, resolvemos várias aplicações com sistemas de equações lineares. Nesta seção, veremos alguns tipos específicos de aplicativos que relacionam duas quantidades. Vamos traduzir as palavras em equações lineares, decidir qual é o método mais conveniente de usar e depois resolvê-las.

    Usaremos nossa estratégia de resolução de problemas para sistemas de equações lineares.

    USE UMA ESTRATÉGIA DE RESOLUÇÃO DE PROBLEMAS PARA SISTEMAS DE EQUAÇÕES LINEARES.

    1. Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
    2. Identifique o que estamos procurando.
    3. Diga o que estamos procurando. Escolha variáveis para representar essas quantidades.
    4. Traduza em um sistema de equações.
    5. Resolva o sistema de equações usando boas técnicas de álgebra.
    6. Verifique a resposta do problema e verifique se faz sentido.
    7. Responda à pergunta com uma frase completa.

    Traduzir para um sistema de equações

    Muitos dos problemas que resolvemos em aplicações anteriores estavam relacionados a duas quantidades. Aqui estão dois exemplos do capítulo sobre Modelos Matemáticos.

    • A soma de dois números é menos quatorze. Um número é quatro a menos que o outro. Encontre os números.
    • Um casal junto ganha $110.000 por ano. A esposa ganha $16.000 a menos do que o dobro do que o marido ganha. O que o marido ganha?

    Nesse capítulo, traduzimos cada situação em uma equação usando apenas uma variável. Às vezes, era um pouco difícil descobrir como nomear as duas quantidades, não era?

    Vamos ver como podemos traduzir esses dois problemas em um sistema de equações com duas variáveis. Vamos nos concentrar nas etapas 1 a 4 de nossa estratégia de solução de problemas.

    Exercício\(\PageIndex{1}\): How to Translate to a System of Equations

    Traduza para um sistema de equações:

    A soma de dois números é menos quatorze. Um número é quatro a menos que o outro. Encontre os números.

    Responda

    Essa figura tem quatro linhas e três colunas. A primeira linha diz: “Etapa 1: Leia o problema. Certifique-se de entender todas as palavras e ideias. Isso é um problema numérico. A soma de dois números é menos quatorze. Um número é quatro a menos que o outro. Encontre os números.”A segunda linha diz: “Etapa 2: Identifique o que você está procurando. 'Encontre os números. ' Estamos procurando 2 números.”A terceira linha diz: “Etapa 3: nomeie o que você está procurando. Escolha variáveis para representar essas quantidades. Usaremos duas variáveis, m e n. Deixe-me = um número n = segundo número.”A quarta linha diz: “Etapa 4: Traduza em um sistema de equações. Escreveremos uma equação para cada frase.” A figura então mostra como “A soma dos números é -14” se torna m + n = -14 e “Um número é quatro a menos que o outro” se torna m = n — 4. A figura então diz: “O sistema é m + n = -14 e m = n — 4”.

    Exercício\(\PageIndex{2}\)

    Traduza para um sistema de equações:

    A soma de dois números é menos vinte e três. Um número é 7 a menos que o outro. Encontre os números.

    Responda

    \(\left\{\begin{array}{l}{m+n=-23} \\ {m=n-7}\end{array}\right.\)

    Exercício\(\PageIndex{3}\)

    Traduza para um sistema de equações:

    A soma de dois números é menos dezoito. Um número é 40 a mais que o outro. Encontre os números.

    Responda

    \(\left\{\begin{array}{l}{m+n=-18} \\ {m=n+40}\end{array}\right.\)

    Faremos outro exemplo em que paramos depois de escrevermos o sistema de equações.

    Exercício\(\PageIndex{4}\)

    Traduza para um sistema de equações:

    Um casal junto ganha $110.000 por ano. A esposa ganha $16.000 a menos do que o dobro do que o marido ganha. O que o marido ganha?

    Responda

    \(\begin{array}{ll}{\text {We are looking for the amount that }} & {\text {Let } h=\text { the amount the husband earns. }} \\ {\text {the husband and wife each earn. }} & { w=\text { the amount the wife earns }} \\ {\text{Translate.}} & {\text{A married couple together earns \$110,000.} }\\ {} & {w+h=110000} \\ & \text{The wife earns \$16,000 less than twice what} \\ & \text{husband earns.} \\ & w=2h−16,000 \\ \text{The system of equations is:} & \left\{\begin{array}{l}{w+h=110,000} \\ {w=2 h-16,000}\end{array}\right.\end{array}\)

    Exercício\(\PageIndex{5}\)

    Traduza para um sistema de equações:

    Um casal tem uma renda familiar total de $84.000. O marido ganha $18.000 a menos do que o dobro do que a esposa ganha. Quanto a esposa ganha?

    Responda

    \(\left\{\begin{array}{l}{w+h=84,000} \\ {h=2 w-18,000}\end{array}\right.\)

    Exercício\(\PageIndex{6}\)

    Traduza para um sistema de equações:

    Um funcionário sênior ganha $5 a menos do que o dobro do que um novo funcionário ganha por hora. Juntos, eles ganham $43 por hora. Quanto ganha cada funcionário por hora?

    Responda

    \(\left\{\begin{array}{l}{s=2 n-5} \\ {s+n=43}\end{array}\right.\)

    Resolva aplicativos de tradução direta

    Configuramos, mas não resolvemos, os sistemas de equações em Exercício\(\PageIndex{1}\) e Exercício.\(\PageIndex{4}\) Agora vamos traduzir uma situação em um sistema de equações e depois resolvê-la.

    Exercício\(\PageIndex{7}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Devon é 26 anos mais velho que seu filho Cooper. A soma de suas idades é 50. Descubra suas idades.

    Responda
    Etapa 1. Leia o problema.  
    Etapa 2. Identifique o que estamos procurando. Estamos procurando as idades de Devon e Cooper.
    Etapa 3. Diga o que estamos procurando. Deixe d= a idade de Devon.
    c= Idade de Cooper
    Etapa 4. Traduza em um sistema de equações. Devon é 26 anos mais velho que Cooper.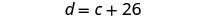
      .
      A soma de suas idades é 50.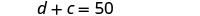
      .
    O sistema é: .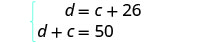
    Etapa 5. Resolva o sistema de equações.

    Resolva por substituição.    		 .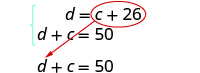
    Substitua c + 26 na segunda equação. .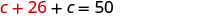
    Resolva para c. .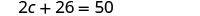
      .
      .
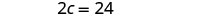
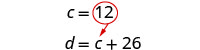
    Substitua c = 12 na primeira equação e resolva por d. .
      .
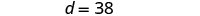
    Etapa 6. Verifique a resposta no problema. A idade de Devon é 26 a mais do que a de Cooper?
    Sim, 38 é 26 a mais do que 12.
    A soma de suas idades é 50?
    Sim, 38 mais 12 é 50.
    Etapa 7. Responda à pergunta. Devon tem 38 anos e Cooper tem 12 anos.
    Exercício\(\PageIndex{8}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Ali é 12 anos mais velho que sua irmã mais nova, Jameela. A soma de suas idades é 40. Descubra suas idades.

    Responda

    Ali tem 26 anos e Jameela tem 14.

    Exercício\(\PageIndex{9}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    O pai de Jake tem 6 anos a mais que 3 vezes a idade de Jake. A soma de suas idades é 42. Descubra suas idades.

    Responda

    Jake tem 9 anos e seu pai tem 33.

    Exercício\(\PageIndex{10}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Quando Jenna passou 10 minutos no aparelho elíptico e depois treinou em circuito por 20 minutos, seu aplicativo de fitness diz que ela queimou 278 calorias. Quando ela passou 20 minutos no aparelho elíptico e 30 minutos treinando em circuito, ela queimou 473 calorias. Quantas calorias ela queima por minuto no aparelho elíptico? Quantas calorias ela queima por cada minuto de treinamento em circuito?

    Responda
    Etapa 1. Leia o problema.  
    Etapa 2. Identifique o que estamos procurando. Estamos procurando o número de
    calorias queimadas a cada minuto no
    aparelho elíptico e a cada minuto de treinamento em
    circuito.
    Etapa 3. Diga o que estamos procurando. Seja e= número de calorias queimadas por minuto no aparelho elíptico.
    c= número de calorias queimadas por minuto durante o treinamento em circuito
    Etapa 4. Traduza em um sistema de equações. 10 minutos no
    treinamento elíptico e em circuito por 20 minutos, queimou
    278 calorias
      .
      20 minutos no elíptico e
    30 minutos de treinamento em circuito queimaram
    473 calorias
      .
    O sistema é: .
    Etapa 5. Resolva o sistema de equações.  
    Multiplique a primeira equação por −2 para obter coeficientes opostos de e. .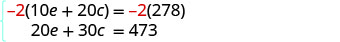
    Simplifique e adicione as equações.

    Resolva para c.    		 .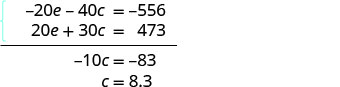
    Substitua c = 8,3 em uma das equações originais para resolver e. .
      .
      .
      .
      .
    Etapa 6. Verifique a resposta no problema. Verifique a matemática por conta própria.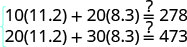
    .  
    Etapa 7. Responda à pergunta. Jenna queima 8,3 calorias por minuto de treinamento em
    circuito e 11,2 calorias por
    minuto enquanto usa o aparelho elíptico.
    Exercício\(\PageIndex{11}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Mark foi para a academia e fez 40 minutos de ioga quente Bikram e 10 minutos de macacos de salto. Ele queimou 510 calorias. Na próxima vez que ele foi à academia, ele fez 30 minutos de ioga quente Bikram e 20 minutos de macacos de salto queimando 470 calorias. Quantas calorias foram queimadas em cada minuto de ioga? Quantas calorias foram queimadas para cada minuto de pular valetes?

    Responda

    Mark queimou 11 calorias para cada minuto de ioga e 7 calorias para cada minuto de pular valetes.

    Exercício\(\PageIndex{12}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Erin passou 30 minutos na máquina de remo e 20 minutos levantando pesos na academia e queimou 430 calorias. Durante sua próxima visita à academia, ela passou 50 minutos na máquina de remo e 10 minutos levantando pesos e queimando 600 calorias. Quantas calorias ela queimou a cada minuto na máquina de remo? Quantas calorias ela queimou em cada minuto de levantamento de peso?

    Responda

    Erin queimou 11 calorias por minuto na máquina de remo e 5 calorias para cada minuto de levantamento de peso.

    Resolva aplicações de geometria

    Quando aprendemos sobre modelos matemáticos, resolvemos aplicações de geometria usando propriedades de triângulos e retângulos. Agora, adicionaremos à nossa lista algumas propriedades dos ângulos.

    As medidas de dois ângulos complementares somam 90 graus. As medidas de dois ângulos suplementares somam 180 graus.

    ÂNGULOS COMPLEMENTAR E SUPLEMENTAR

    Dois ângulos são complementares se a soma das medidas de seus ângulos for de 90 graus.

    Dois ângulos são complementares se a soma das medidas de seus ângulos for 180 graus.

    Se dois ângulos são complementares, dizemos que um ângulo é o complemento do outro.

    Se dois ângulos são complementares, dizemos que um ângulo é o complemento do outro.

    Exercício\(\PageIndex{13}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    A diferença de dois ângulos complementares é de 26 graus. Encontre as medidas dos ângulos.

    Responda

    \(\begin{array}{ll}{\textbf {Step 1. Read}\text{ the problem. }} & {} \\ {\textbf {Step 2. Identify}\text{ what we are looking for.}} & {\text {We are looking for the measure of each angle.}} \\ \\ {\textbf{Step 3. Name}\text{ what we are looking for.}} & {\text{Let x = the measure of the first angle.} }\\ {} & \text{y = the measure of the second angle} \\ \textbf{Step 4. Translate}\text{ into a system of equations.}& \text{The angles are complementary.} \\ & \text{x+y=90} \\ & \text{The difference of the two angles is 26 degrees.} \\ & \text{x−y=26} \\ \\ \text{The system is} & {\left\{\begin{array}{l}{x+y=90} \\ {x-y=26}\end{array}\right.} \\ \textbf{Step 5. Solve}\text{ the system of equations by elimination.} \\& \left\{\begin{array}{l}{x+y=90} \\ \underline{x-y=26}\end{array}\right. \\ & \quad2x\quad=116 \\ \text{Substitute x = 58 into the first equation.}& \begin{array}{lrll} &x&=&58 \\ &x+y&=&90 \\ &58+y&=&90 \\ &y&=&32\end{array} \\ \textbf{Step 6. Check}\text{ the answer in the problem.} & \\ 58+32=90\checkmark\\ 58-32=36\checkmark \\ \\ \textbf{Step 7. Answer}\text{ the question.} & \text{The angle measures are 58 degrees and 32 degrees.}\end{array}\)

    Exercício\(\PageIndex{14}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    A diferença de dois ângulos complementares é de 20 graus. Encontre as medidas dos ângulos.

    Responda

    As medidas do ângulo são 55 graus e 35 graus.

    Exercício\(\PageIndex{15}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    A diferença de dois ângulos complementares é de 80 graus. Encontre as medidas dos ângulos.

    Responda

    As medidas do ângulo são 5 graus e 85 graus.

    Exercício\(\PageIndex{16}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Dois ângulos são complementares. A medida do ângulo maior é doze graus menor que cinco vezes a medida do ângulo menor. Encontre as medidas dos dois ângulos.

    Responda
    Etapa 1. Leia o problema.  
    Etapa 2. Identifique o que estamos procurando. Estamos procurando a medida de cada ângulo.
    Etapa 3. Diga o que estamos procurando. Seja x= a medida do primeiro ângulo.
    y= a medida do segundo ângulo
    Etapa 4. Traduza em um sistema de equações. Os ângulos são complementares.
      .
      O ângulo maior é doze a menos de cinco vezes o ângulo menor.
      .
    O sistema é:


    Etapa 5. Resolva o sistema de substituição de equações.    		 .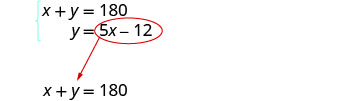
    Substitua 5 x − 12 por y na primeira equação. .
    Resolva para x. .
      .
      .
    Substitua 32 por na segunda equação e resolva por y. .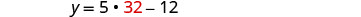
      .
      .
    Etapa 6. Verifique a resposta no problema.

    \(\begin{aligned} 32+158 &=180 \checkmark \\ 5 \cdot 32-12 &=147 \checkmark \end{aligned}\)    		  
    Etapa 7. Responda à pergunta. As medidas do ângulo são 148 e 32.
    Exercício\(\PageIndex{17}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Dois ângulos são complementares. A medida do ângulo maior é 12 graus a mais do que três vezes o ângulo menor. Encontre as medidas dos ângulos.

    Responda

    As medidas do ângulo são 42 graus e 138 graus.

    Exercício\(\PageIndex{18}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Dois ângulos são complementares. A medida do ângulo maior é 18 a menos que o dobro da medida do ângulo menor. Encontre as medidas dos ângulos.

    Responda

    As medidas do ângulo são 66 graus e 114 graus.

    Exercício\(\PageIndex{19}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Randall tem 125 pés de cerca para cercar a parte retangular de seu quintal adjacente à sua casa. Ele só precisará cercar três lados, porque o quarto lado será a parede da casa. Ele quer que o comprimento do pátio cercado (paralelo à parede da casa) seja 5 pés a mais do que quatro vezes maior que a largura. Encontre o comprimento e a largura.

    Responda
    Etapa 1. Leia o problema.  
    Etapa 2. Identifique o que você está procurando. Estamos procurando o comprimento e a largura.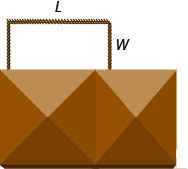
      .
    Etapa 3. Diga o que estamos procurando. Seja L = o comprimento do pátio cercado.
    W= a largura do pátio cercado
    Etapa 4. Traduza em um sistema de equações. Um comprimento e duas larguras equivalem a 125.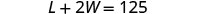
      .
      O comprimento será 5 pés a mais do que quatro vezes a largura.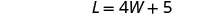
      .
    O sistema é:

    Etapa 5. Resolva o sistema de equações por substituição.    		 .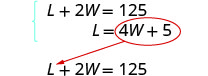
    Substitua L = 4 W + 5 na primeira
    equação e resolva por W.    		 .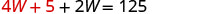
      .
      .
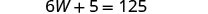
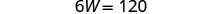
    Substitua 20 por W na segunda
    equação e resolva por L.    		 .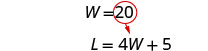
      .
      .
      .
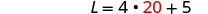
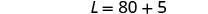
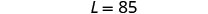
    Etapa 6. Verifique a resposta no problema.

    \(\begin{array}{rll} 20+28+20&=&125\checkmark \\ 85 &=&4\cdot 20 + 5\checkmark\end{array}\)    		  
    Etapa 7. Responda à equação. O comprimento é 85 pés e a largura é 20 pés.
    Exercício\(\PageIndex{20}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Mario quer colocar uma cerca retangular ao redor da piscina em seu quintal. Como um lado é adjacente à casa, ele só precisará cercar três lados. Existem dois lados longos e o menor é paralelo à casa. Ele precisa de 155 pés de cerca para cercar a piscina. O comprimento do lado comprido é 10 pés a menos que o dobro da largura. Encontre o comprimento e a largura da área da piscina a ser fechada.

    Responda

    O comprimento é de 60 pés e a largura é de 35 pés.

    Exercício\(\PageIndex{21}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Alexis quer construir uma corrida retangular para cães em seu quintal, ao lado da cerca do vizinho. Ela usará 136 pés de cerca para cercar completamente a corrida retangular para cães. O comprimento do cão percorrido ao longo da cerca do vizinho será 16 pés a menos que o dobro da largura. Encontre o comprimento e a largura da corrida de cães.

    Responda

    O comprimento é 60 pés e a largura é 38 pés.

    Resolva aplicações de movimento uniforme

    Usamos uma tabela para organizar as informações em problemas de movimento uniforme quando as apresentamos anteriormente. Continuaremos usando a tabela aqui. A equação básica era D = rt, onde D é a distância percorrida, r é a taxa e t é o tempo.

    Nosso primeiro exemplo de aplicação de movimento uniforme será para uma situação semelhante a algumas que já vimos, mas agora podemos usar duas variáveis e duas equações.

    Exercício\(\PageIndex{22}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Joni deixou St. Louis na interestadual, dirigindo para o oeste em direção a Denver a uma velocidade de 65 milhas por hora. Meia hora depois, Kelly deixou St. Louis na mesma rota que Joni, dirigindo 78 milhas por hora. Quanto tempo Kelly levará para alcançar Joni?

    Responda

    Um diagrama é útil para nos ajudar a visualizar a situação.

    Esta figura mostra um diagrama. Denver está à esquerda e St. Louis está à direita. Há um raio que se estende de St. Louis a Denver. É rotulado como “Joni” e “65 m p h.” Há outro raio que se estende de St. Louis a Denver. É rotulado como “Kelly (meia hora depois)” e “78 m p h”.

    Identifique e nomeie o que estamos procurando.
    Um gráfico nos ajudará a organizar os dados.
    Conhecemos as taxas de Joni e Kelly e, por isso, as
    inserimos no gráfico.    		  
    Estamos procurando por quanto tempo Kelly,
    k e Joni, j, cada um dirigirá.
    Como D = R · t, podemos preencher a coluna Distância.    		 .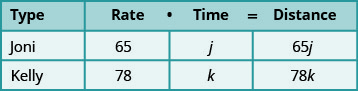
    Traduza em um sistema de equações.
    Para criar o sistema de equações, devemos reconhecer que Kelly e Joni dirigirão na mesma distância. Então, 65j=78k.

    Além disso, como Kelly saiu mais tarde, seu tempo será de 12 a 12 horas a menos que o tempo de Joni.

    Então, k=j−12.
    Agora temos o sistema. .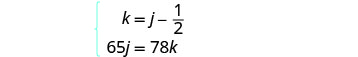
    Resolva o sistema de equações por substituição. .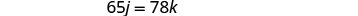
    Substitua k=j−12 na segunda equação e resolva por j. .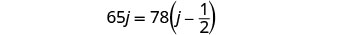
      .
      .
      .
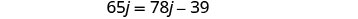
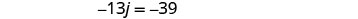
    Para encontrar o tempo de Kelly, substitua j = 3 na primeira equação e resolva por k. .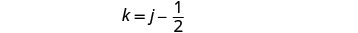
      .
      .
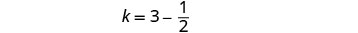
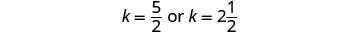
    Verifique a resposta no problema.
    Joni 3 horas (65 mph) = 195 milhas.
    \(2\frac{1}{2}\)Horas de Kelly (78 mph) = 195 milhas.
    Sim, eles terão percorrido a mesma distância
    quando se encontrarem.    		  
    Responda à pergunta. Kelly alcançará Joni em\(2\frac{1}{2}\) horas.
    Até lá, Joni terá viajado 3 horas.
    Exercício\(\PageIndex{23}\)

    Traduza para um sistema de equações e resolva: Mitchell deixou Detroit na interestadual dirigindo para o sul em direção a Orlando a uma velocidade de 60 milhas por hora. Clark deixou Detroit 1 hora depois viajando a uma velocidade de 75 milhas por hora, seguindo a mesma rota de Mitchell. Quanto tempo Clark vai levar para pegar Mitchell?

    Responda

    Clark levará 4 horas para pegar Mitchell.

    Exercício\(\PageIndex{24}\)

    Traduza para um sistema de equações e resolva: Charlie saiu da casa de sua mãe viajando a uma velocidade média de 36 milhas por hora. Sua irmã Sally saiu 15 minutos (1/4 hora) depois viajando pela mesma rota a uma velocidade média de 42 milhas por hora. Quanto tempo falta para Sally alcançar Charlie?

    Responda

    Sally levará\(1\frac{1}{2}\) horas para alcançar Charlie.

    Muitas aplicações reais de movimento uniforme surgem devido aos efeitos das correntes — da água ou do ar — na velocidade real de um veículo. Os voos de avião de cross-country nos Estados Unidos geralmente demoram mais para o oeste do que para o leste devido às correntes de vento predominantes.

    Vamos dar uma olhada em um barco viajando em um rio. Dependendo da direção em que o barco está indo, a corrente da água o está diminuindo ou acelerando.

    A figura\(\PageIndex{1}\) e a figura\(\PageIndex{2}\) mostram como a corrente de um rio afeta a velocidade com que um barco está realmente viajando. Chamaremos a velocidade do barco na água parada b e a velocidade da corrente do rio c.

    Na Figura,\(\PageIndex{1}\) o barco está indo rio abaixo, na mesma direção da corrente do rio. A corrente ajuda a empurrar o barco, então a velocidade real do barco é mais rápida do que sua velocidade em águas paradas. A velocidade real na qual o barco está se movendo é b + c.

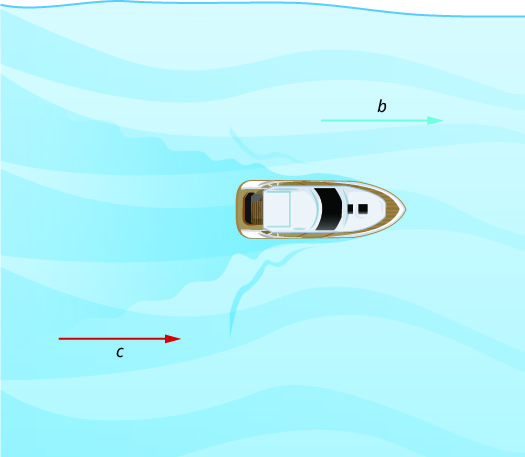
    Esta figura mostra um barco flutuando na água. À direita, há uma seta apontando para o barco. É rotulado como “c”. À esquerda, há uma seta apontando para longe do barco. É rotulado como “b”.
    Figura\(\PageIndex{1}\)

    Na Figura,\(\PageIndex{2}\) o barco está indo rio acima, em frente à corrente do rio. A corrente está indo contra o barco, então a velocidade real do barco é mais lenta do que sua velocidade em água parada. A velocidade real do barco é b−c.

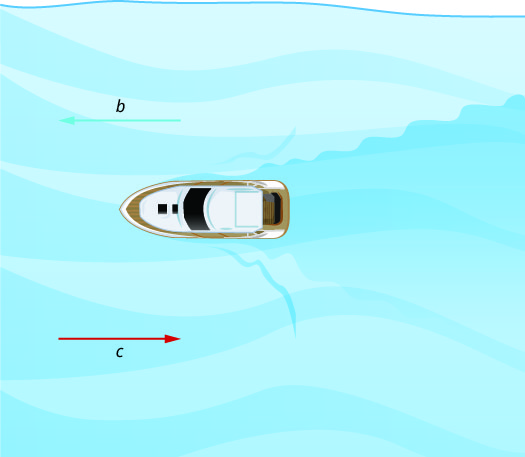
    Esta figura mostra um barco flutuando na água. À esquerda está uma seta apontando para longe do barco chamada “b” e uma seta apontando para o barco com “c”.
    Figura\(\PageIndex{2}\)

    Colocaremos alguns números nessa situação no Exercício\(\PageIndex{25}\).

    Exercício\(\PageIndex{25}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Um navio de cruzeiro fluvial navegou 60 milhas rio abaixo por 4 horas e depois levou 5 horas navegando rio acima para retornar ao cais. Encontre a velocidade do navio na água parada e a velocidade da corrente do rio.

    Responda

    Leia o problema.

    Esse é um problema de movimento uniforme e uma imagem nos ajudará a visualizar a situação.

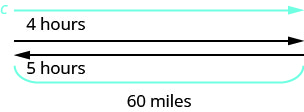
    Esta figura mostra uma seta chamada “c” que continua à direita, representando a onda. Sob a onda, há um raio que aponta para a direita e é rotulado como “quatro horas”. Sob esse raio está outro raio apontando para a esquerda chamado “cinco horas”. Tem a mesma duração do raio rotulado como “quatro horas”. Há um suporte sob o raio chamado “cinco horas”. O colchete é rotulado como “60 milhas”.

    Identifique o que estamos procurando. Estamos procurando a velocidade do navio
    em águas paradas e a velocidade da corrente.
    Diga o que estamos procurando. Seja s=s= a taxa do navio em água parada.
    c=c= a taxa da corrente
    Um gráfico nos ajudará a organizar as informações.
    O navio vai rio abaixo e depois rio acima.
    Indo rio abaixo, a corrente ajuda o
    navio; portanto, a taxa real do navio é s + c.
    Indo rio acima, a corrente desacelera o navio;
    portanto, a taxa real é s − c.    		 .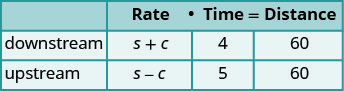
    A jusante, leva 4 horas.
    A montante leva 5 horas.
    Em cada sentido, a distância é de 60 milhas.    		  
    Traduza em um sistema de equações.
    Como a taxa vezes o tempo é a distância, podemos
    escrever o sistema de equações.    		 .
    Resolva o sistema de equações.
    Distribua para colocar as duas equações na
    forma padrão e resolva por eliminação.    		 .
    Multiplique a equação superior por 5 e a equação inferior por 4.
    Adicione as equações e resolva para s.    		 .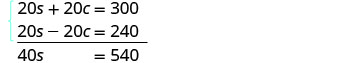
    Substitua s = 13,5 em uma das equações originais. .
      .
      .
      .
     

    5.4-43.jpg
    Verifique a resposta no problema.

    A taxa a jusante seria de
    13,5 + 1,5 = 15 mph.
    Em 4 horas, o navio viajaria
    15 · 4 = 60 milhas.
    A taxa de upstream seria de
    13,5 − 1,5 = 12 mph.
    Em 5 horas, o navio viajaria
    12 · 5 = 60 milhas.    		  
    Responda à pergunta. A taxa do navio é de 13,5 mph e
    a taxa da corrente é de 1,5 mph.
    Exercício\(\PageIndex{26}\)

    Traduza para um sistema de equações e resolva: um cruzeiro de barco pelo rio Mississippi navegou 120 milhas rio acima por 12 horas e depois levou 10 horas para retornar ao cais. Encontre a velocidade do barco fluvial na água parada e a velocidade da corrente do rio.

    Responda

    A taxa do barco é 11 mph e a taxa da corrente é 1 mph.

    Exercício\(\PageIndex{27}\)

    Traduza para um sistema de equações e resolva: Jason remou sua canoa 24 milhas rio acima por 4 horas. Ele levou 3 horas para remar de volta. Encontre a velocidade da canoa na água parada e a velocidade da corrente do rio.

    Responda

    A velocidade da canoa é 7 mph e a velocidade da corrente é 1 mph.

    As correntes de vento afetam a velocidade do avião da mesma forma que as correntes de água afetam a velocidade do barco. Veremos isso no Exercício\(\PageIndex{28}\). Uma corrente de vento na mesma direção em que o avião está voando é chamada de vento de cauda. Uma corrente de vento soprando contra a direção do avião é chamada de vento contrário.

    Exercício\(\PageIndex{28}\)

    Traduza para um sistema de equações e, em seguida, resolva:

    Um jato particular pode voar 1095 milhas em três horas com vento de cauda, mas apenas 987 milhas em três horas em um vento contrário. Encontre a velocidade do jato no ar parado e a velocidade do vento.

    Responda

    Leia o problema.

    Esse é um problema de movimento uniforme e uma imagem nos ajudará a visualizar.

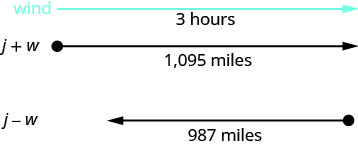
    Esta figura mostra uma seta chamada “3 horas” que continua à direita, representando o vento. Abaixo da onda há um raio que aponta para a direita e é rotulado como “j mais w é igual a 365” e “1.095 milhas”. Sob esse raio está outro raio apontando para a esquerda chamado “j menos w é igual a 329” e “987 milhas”.

    Identifique o que estamos procurando. Estamos procurando a velocidade do jato
    no ar parado e a velocidade do vento.
    Diga o que estamos procurando. Seja j= a velocidade do jato no ar parado.
    w= a velocidade do vento
    Um gráfico nos ajudará a organizar as informações.
    O jato faz duas viagens: uma com vento de cauda
    e outra em vento contrário.
    Em um vento de cauda, o vento ajuda o jato e, portanto,
    a taxa é j + w.
    Em um vento contrário, o vento desacelera o jato e
    , portanto, a taxa é j − w.    		 .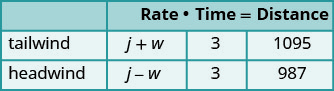
    Cada viagem dura 3 horas.
    Em um vento de cauda, o jato voa 1.095 milhas.
    Em um vento contrário, o jato voa 987 milhas.    		  
    Traduza em um sistema de equações.
    Como taxa vezes tempo é distância, obtemos o
    sistema de equações.    		 .
    Resolva o sistema de equações.
    Distribua e resolva por eliminação.    		 .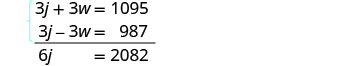
    Adicione e resolva para j.

    Substitua j = 347 em uma das
    equações originais e resolva por w.    		 .
      .
      .
      .
      .
    Verifique a resposta no problema.

    Com o vento de cauda, a taxa real do
    jato seria
    347 + 18 = 365 mph.
    Em 3 horas, o jato viajaria
    365 · 3 = 1095 milhas.
    Indo para o vento contrário, a
    taxa real do jato seria
    347 − 18 = 329 mph.
    Em 3 horas, o jato viajaria
    329 · 3 = 987 milhas.    		  
    Responda à pergunta. A taxa do jato é de 347 mph e a
    taxa do vento é de 18 mph.
    Exercício\(\PageIndex{29}\)

    Traduza para um sistema de equações e resolva: um pequeno jato pode voar 1.325 milhas em 5 horas com vento de cauda, mas apenas 1.025 milhas em 5 horas em um vento contrário. Encontre a velocidade do jato no ar parado e a velocidade do vento.

    Responda

    A velocidade do jato é 235 mph e a velocidade do vento é 30 mph.

    Exercício\(\PageIndex{30}\)

    Traduza para um sistema de equações e resolva: um jato comercial pode voar 1728 milhas em 4 horas com vento de cauda, mas apenas 1536 milhas em 4 horas em um vento contrário. Encontre a velocidade do jato no ar parado e a velocidade do vento.

    Responda

    A velocidade do jato é 408 mph e a velocidade do vento é de 24 mph.

    Glossário

    ângulos complementares
    Dois ângulos são complementares se a soma das medidas de seus ângulos for em\(90\) graus.
    ângulos suplementares
    Dois ângulos são complementares se a soma das medidas de seus ângulos for\(180\) graus.