Capítulo 4 Exercícios de revisão
- Page ID
- 184191
Capítulo 4 Exercícios de revisão
Sistema de coordenadas retangulares
Traçar pontos em um sistema de coordenadas retangulares
Nos exercícios a seguir, plote cada ponto em um sistema de coordenadas retangular.
- (−1, −5)
- (−3,4)
- (2, −3)
- \(\left(1, \frac{5}{2}\right)\)
- (4,3)
- (−4,3)
- (−4, −3)
- (4, −3)
- Resposta
-
- (−2,0)
- (0, −4)
- (0,5)
- (3,0)
- \(\left(2, \frac{3}{2}\right)\)
- \(\left(3, \frac{4}{3}\right)\)
- \(\left(\frac{1}{3},-4\right)\)
- \(\left(\frac{1}{2},-5\right)\)
- Resposta
-
Identificar pontos em um gráfico
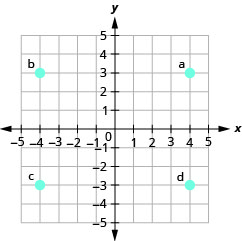
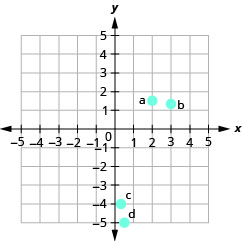
Nos exercícios a seguir, nomeie o par ordenado de cada ponto mostrado no sistema de coordenadas retangulares.
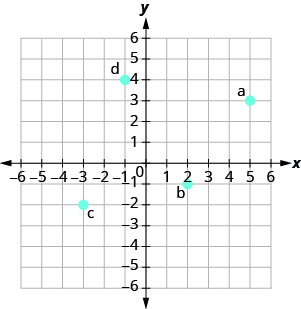
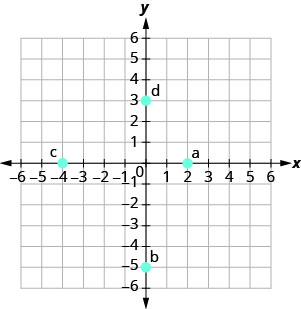
- Resposta
-
uma. (2,0)
b (0, −5)
c (−4,0)
d (0,3)
Verificar soluções para uma equação em duas variáveis
Nos exercícios a seguir, quais pares ordenados são soluções para as equações dadas?
\(5x+y=10\)
- (5,1)
- (2,0)
- (4,−10)
\(y=6x−2\)
- (1,4)
- \(\left(\frac{1}{3}, 0\right)\)
- (6, −2)
- Resposta
-
1, 2
Complete uma tabela de soluções para uma equação linear em duas variáveis
Nos exercícios a seguir, complete a tabela para encontrar soluções para cada equação linear.
\(y=4 x-1\)
| x | y | (x, y) |
| 0 | ||
| 1 | ||
| -2 |
\(y=-\frac{1}{2} x+3\)
| x | y | (x, y) |
| 0 | ||
| 4 | ||
| -2 |
- Resposta
-
x y (x, y) 0 3 (0,3) 4 1 (4, 1) −2 4 (−2,4)
\(x+2 y=5\)
| x | y | (x, y) |
| 0 | ||
| 1 | ||
| -1 |
\(3x+2y=6\)
| x | y | (x, y) |
| 0 | ||
| 0 | ||
| -2 |
- Resposta
-
x y (x, y) 0 −3 (0, −3) 2 0 (2,0) −2 −6 (−2, −6)
Encontre soluções para uma equação linear em duas variáveis
Nos exercícios a seguir, encontre três soluções para cada equação linear.
\(x+y=3\)
\(x+y=-4\)
- Resposta
-
As respostas podem variar.
\(y=3 x+1\)
\(y=-x-1\)
- Resposta
-
As respostas podem variar.
Representação gráfica de equações lineares
Reconhecer a relação entre as soluções de uma equação e seu gráfico
Nos exercícios a seguir, para cada par ordenado, decida:
- O par ordenado é uma solução para a equação?
- O ponto está na linha?
\(y=−x+4\)
(0,4) (−1,3)
(2,2) (−2,6)
\(y=\frac{2}{3} x-1\)
\((0,-1) (3,1)\)
\((-3,-3) (6,4)\)
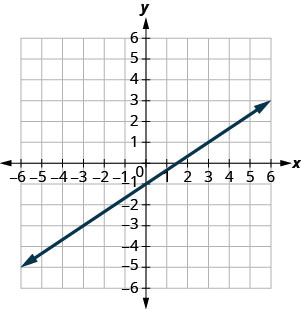
- Resposta
-
- sim; sim
- sim; não
Representar graficamente uma equação linear traçando pontos
Nos exercícios a seguir, desenhe graficamente pontos.
\(y=4x-3\)
\(y=-3x\)
- Resposta
-
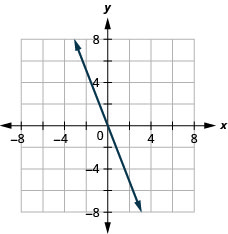
\(y=\frac{1}{2} x+3\)
\(x-y=6\)
- Resposta
-
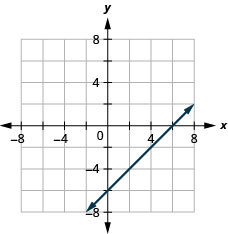
\(2x+y=7\)
\(3x-2y=6\)
- Resposta
-
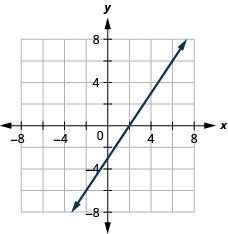
Gráfico de linhas verticais e horizontais
Nos exercícios a seguir, represente graficamente cada equação.
\(y=-2\)
\(x=3\)
- Resposta
-
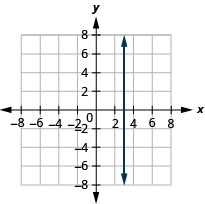
Nos exercícios a seguir, represente graficamente cada par de equações no mesmo sistema de coordenadas retangulares.
\(y=-2 x\)e\(y=-2\)
\(y=\frac{4}{3} x\)e\(y=\frac{4}{3}\)
- Resposta
-
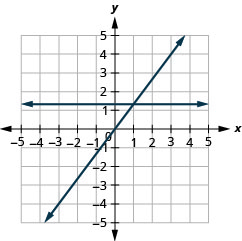
Representação gráfica com interceptações
Identifique as\(y\) interceptações\(x\) - e -em um gráfico
Nos exercícios a seguir, encontre as\(y\) interceptações\(x\) - e -.
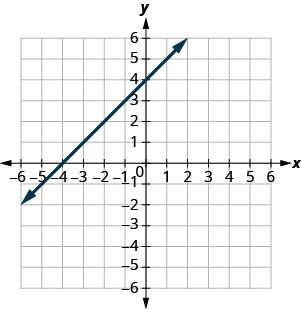
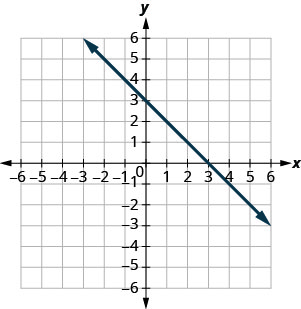
- Resposta
-
\((3,0)\)e\((0,3)\)
Encontre as\(y\) interceptações\(x\) - e -de uma equação de uma reta
Nos exercícios a seguir, encontre os interceptos de cada equação.
\(x+y=5\)
\(x-y=-1\)
- Resposta
-
\((-1,0),(0,1)\)
\(x+2y=6\)
\(2x+3y=12\)
- Resposta
-
\((6,0),(0,4)\)
\(y=\frac{3}{4} x-12\)
\(y=3x\)
- Resposta
-
\((0,0)\)
Representar graficamente uma linha usando as interceptações
Nos exercícios a seguir, faça um gráfico usando os interceptos.
\(-x+3y=3\)
\(x+y=-2\)
- Resposta
-
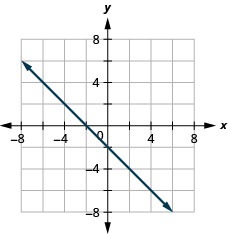
\(x-y=4\)
\(2x-y=5\)
- Responda
-
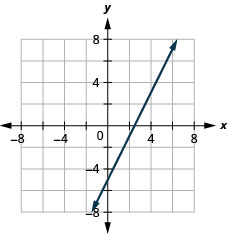
\(2x-4y=8\)
\(y=2x\)
- Responda
-
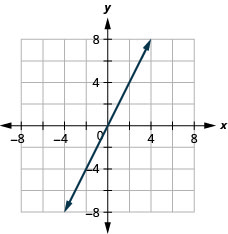
Inclinação de uma linha
Use placas geográficas para modelar a inclinação
Nos exercícios a seguir, encontre a inclinação modelada em cada geoboard.
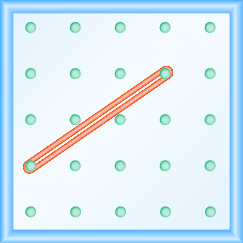
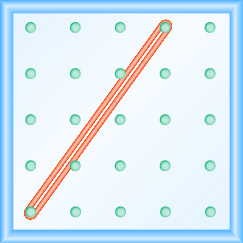
- Responda
-
\(\frac{4}{3}\)
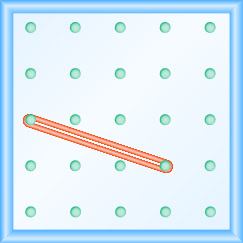
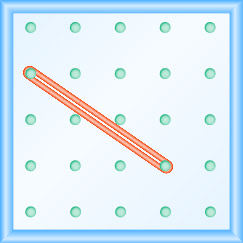
- Responda
-
\(-\frac{2}{3}\)
\(\frac{1}{3}\)
\(\frac{3}{2}\)
- Responda
-
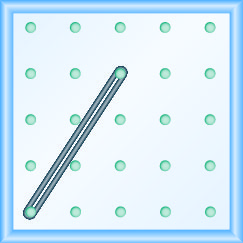
\(-\frac{2}{3}\)
\(-\frac{1}{2}\)
- Responda
-
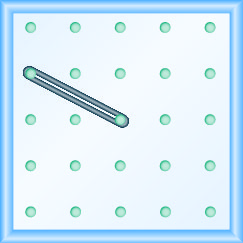
Use\(m=\frac{\text { rise }}{\text { run }}\) para encontrar a inclinação de uma reta a partir de seu gráfico
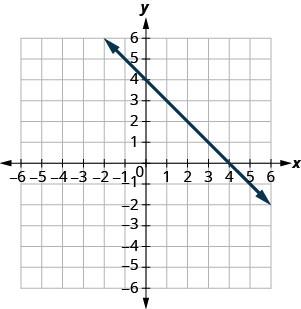
Nos exercícios a seguir, encontre a inclinação de cada linha mostrada.
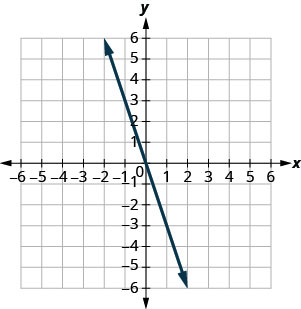
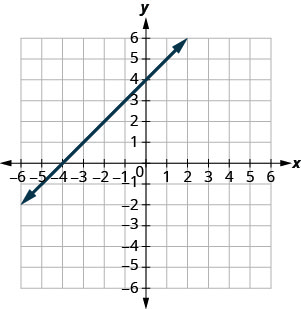
- Responda
-
1
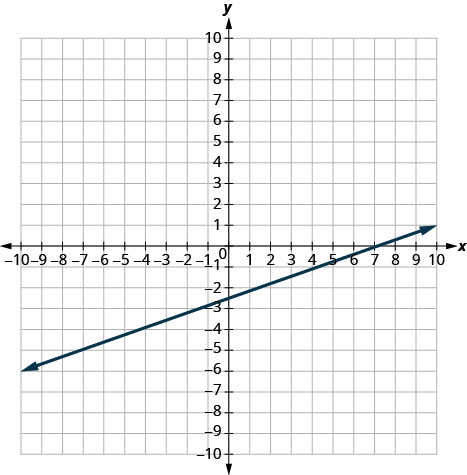
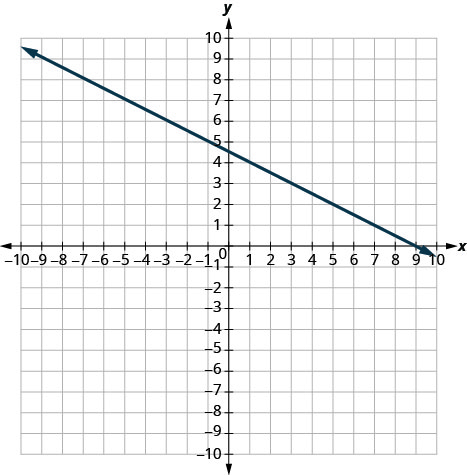
- Responda
-
\(-\frac{1}{2}\)
Encontre a inclinação das linhas horizontais e verticais
Nos exercícios a seguir, encontre a inclinação de cada linha.
\(y=2\)
\(x=5\)
- Responda
-
indefinida
\(x=-3\)
\(y=-1\)
- Responda
-
0
Use a fórmula de inclinação para encontrar a inclinação de uma linha entre dois pontos
Nos exercícios a seguir, use a fórmula da inclinação para encontrar a inclinação da linha entre cada par de pontos.
\((-1,-1),(0,5)\)
\((3,5),(4,-1)\)
- Responda
-
−6
\((-5,-2),(3,2)\)
\((2,1),(4,6)\)
- Responda
-
\(\frac{5}{2}\)
Representar graficamente uma linha com um ponto e a inclinação
Nos exercícios a seguir, represente graficamente cada linha com o ponto e a inclinação fornecidos.
\((2,-2) ; \quad m=\frac{5}{2}\)
\((-3,4) ; \quad m=-\frac{1}{3}\)
- Responda
-
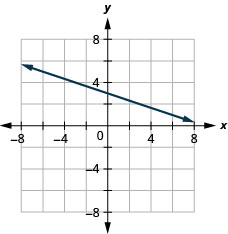
\(x\)-interceptar\(-4 ; \quad m=3\)
\(y\)-interceptar\(1 ; \quad m=-\frac{3}{4}\)
- Responda
-
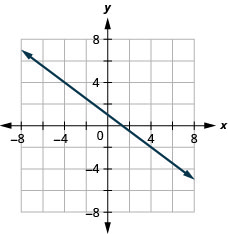
Resolva aplicações de inclinação
Nos exercícios a seguir, resolva essas aplicações de inclinação.
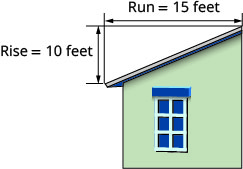
O telhado na foto abaixo tem uma elevação de\(10\) pés e uma corrida de\(15\) pés. Qual é sua inclinação?
Uma estrada de montanha sobe\(50\) pés para uma corrida\(500\) de 3 pés. Qual é sua inclinação?
- Responda
-
\(\frac{1}{10}\)
Forma de interceptação de uma equação de uma reta
Reconhecer a relação entre o gráfico e a forma inclinada-interceptação de uma equação de uma reta
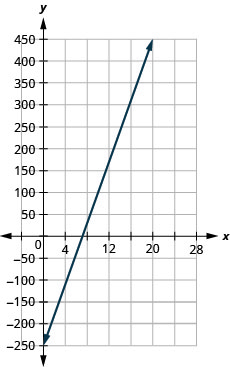
Nos exercícios a seguir, use o gráfico para encontrar a inclinação e a interceptação y de cada linha. Compare os valores com a equação\(y=mx+b\).
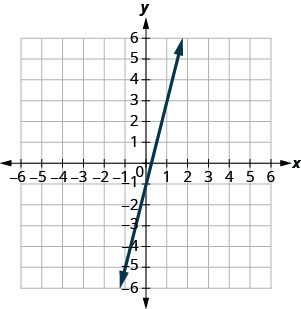
\(y=4x−1\)
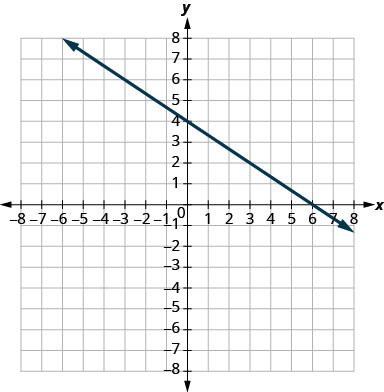
\(y=-\frac{2}{3} x+4\)
- Responda
-
inclinação\(m=-\frac{2}{3}\) e\(y\) interceptação\((0,4)\)
Identifique a inclinação e o intercepto Y a partir de uma equação de uma reta
Nos exercícios a seguir, identifique a inclinação e a\(y\) interceptação de cada linha.
\(y=-4 x+9\)
\(y=\frac{5}{3} x-6\)
- Responda
-
\(\frac{5}{3} ;(0,-6)\)
\(5x+y=10\)
\(4x-5y=8\)
- Responda
-
\(\frac{4}{5} ;\quad \left(0,-\frac{8}{5}\right)\)
Representar graficamente uma linha usando sua inclinação e interceptação
Nos exercícios a seguir, represente graficamente a linha de cada equação usando sua inclinação e\(y\) intercepto.
\(y=2x+3\)
\(y=-x-1\)
- Responda
-
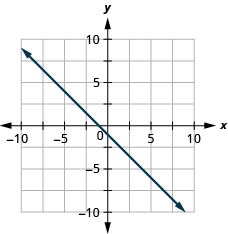
\(y=-\frac{2}{5} x+3\)
\(4x-3y=12\)
- Responda
-
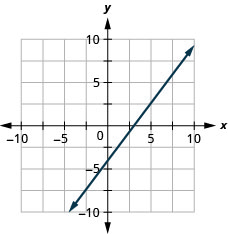
Nos exercícios a seguir, determine o método mais conveniente para representar graficamente cada linha.
\(x=5\)
\(y=-3\)
- Responda
-
linha horizontal
\(2x+y=5\)
\(x-y=2\)
- Responda
-
intercepta
\(y=x+2\)
\(y=\frac{3}{4} x-1\)
- Responda
-
pontos de plotagem
Represente graficamente e interprete aplicações de inclinação-interceptação
Katherine é chef particular. A equação\(C=6.5m+42\) modela a relação entre seu custo semanal\(C\), em dólares e o número de refeições que ela serve.\(m\)
- Encontre o custo de Katherine por uma semana quando ela não serve refeições.
- Encontre o custo de uma semana quando ela serve\(14\) refeições.
- Interprete a inclinação e a\(C\) interceptação da equação.
- Faça um gráfico da equação.
Marjorie ensina piano. A equação\(P=35h−250\) modela a relação entre seu lucro semanal\(P\), em dólares\(s\), e o número de aulas que ela ensina.
- Descubra o lucro de Marjorie por uma semana quando ela não dá aulas para alunos.
- Encontre o lucro de uma semana quando ela dá aulas para\(20\) estudantes.
- Interprete a inclinação e a\(P\) interceptação da equação.
- Faça um gráfico da equação.
- Responda
-
- \(−$250\)
- \($450\)
- A inclinação,\(35\), significa que o lucro semanal de Marjorie\(P\),, aumenta\($35\) em cada aula adicional que ela ensina. O\(P\) -intercept significa que, quando o número de aulas é\(0\), Marjorie perde\($250\).
Use inclinações para identificar linhas paralelas
Nos exercícios a seguir, use inclinações e\(y\) interceptações -para determinar se as linhas são paralelas.
\(4x-3y=-1 ; \quad y=\frac{4}{3} x-3\)
\(2 x-y=8 ; \quad x-2 y=4\)
- Responda
-
não paralelo
Use inclinações para identificar linhas perpendiculares
Nos exercícios a seguir, use inclinações e interceptos y para determinar se as retas são perpendiculares.
\(y=5x-1 ; \quad 10x+2y=0\)
\(3x-2y=5 ; \quad 2x+3y=6\)
- Responda
-
perpendiculares
Encontre a equação de uma reta
Encontre uma equação da reta dada a inclinação e a interceptação y
Nos exercícios a seguir, encontre a equação de uma reta com determinada inclinação e\(y\) intercepto. Escreva a equação na forma inclinação-interceptação.
inclinação\(\frac{1}{3}\) e\(y\) interceptação\((0,-6)\)
inclinação\(-5\) e\(y\) interceptação\((0,-3)\)
- Responda
-
\(y=-5x-3\)
inclinação\(0\) e\(y\) interceptação\((0,4)\)
inclinação\(-2\) e\(y\) interceptação\((0,0)\)
- Responda
-
\(y=-2x\)
Nos exercícios a seguir, encontre a equação da linha mostrada em cada gráfico. Escreva a equação na forma inclinação-interceptação.
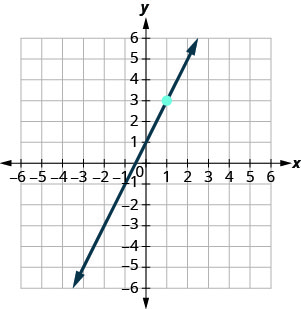
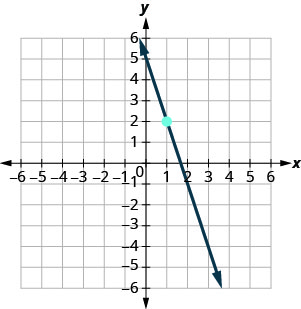
- Responda
-
\(y=-3x+5\)
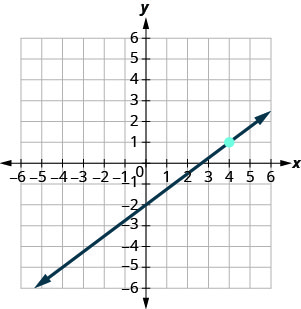
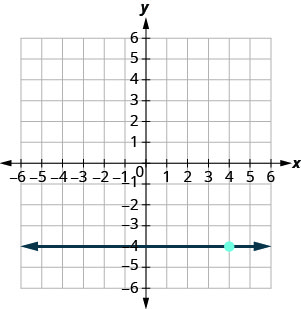
- Responda
-
\(y=-4\)
Encontre uma equação da reta dada a inclinação e um ponto
Nos exercícios a seguir, encontre a equação de uma reta com determinada inclinação e contendo o ponto dado. Escreva a equação na forma inclinação-interceptação.
\(m=-\frac{1}{4},\)ponto\((-8,3)\)
\(m=\frac{3}{5},\)ponto\((10,6)\)
- Responda
-
\(y=\frac{3}{5} x\)
Linha horizontal contendo\((-2,7)\)
\(m=-2,\)ponto\((-1,-3)\)
- Responda
-
\(y=-2x-5\)
Encontre uma equação da reta dados dois pontos
Nos exercícios a seguir, encontre a equação de uma linha contendo os pontos dados. Escreva a equação na forma inclinação-interceptação.
\((2,10)\)e\((-2,-2)\)
\((7,1)\)e\((5,0)\)
- Responda
-
\(y=\frac{1}{2} x-\frac{5}{2}\)
\((3,8)\)e\((3,-4)\)
\((5,2)\)e\((-1,2)\)
- Responda
-
\(y=2\)
Encontre uma equação de uma reta paralela a uma determinada linha
Nos exercícios a seguir, encontre uma equação de uma reta paralela à linha dada e contenha o ponto dado. Escreva a equação na forma inclinação-interceptação.
\(y=-3x+6,\)ponto de linha\((1,-5)\)
\(2x+5y=-10,\)ponto de linha\((10,4)\)
- Responda
-
\(y=-\frac{2}{5} x+8\)
\(x=4,\)ponto de linha\((-2,-1)\)
\(y=-5,\)ponto de linha\((-4,3)\)
- Responda
-
\(y=3\)
Encontre uma equação de uma reta perpendicular a uma determinada linha
Nos exercícios a seguir, encontre uma equação de uma reta perpendicular à linha dada e contenha o ponto dado. Escreva a equação na forma inclinação-interceptação.
\(y=-\frac{4}{5} x+2,\)ponto de linha\((8,9)\)
\(2x-3y=9,\)ponto de linha\((-4,0)\)
- Responda
-
\(y=-\frac{3}{2} x-6\)
\(y=3,\)ponto de linha\((-1,-3)\)
\(x=-5\)ponto de linha\((2,1)\)
- Responda
-
\(y=1\)
Gráfico de desigualdades lineares
Verificar soluções para uma desigualdade em duas variáveis
Nos exercícios a seguir, determine se cada par ordenado é uma solução para a desigualdade dada.
Determine se cada par ordenado é uma solução para a desigualdade\(y<x−3\):
- \((0,1)\)
- \((−2,−4)\)
- \((5,2)\)
- \((3,−1)\)
- \((−1,−5)\)
Determine se cada par ordenado é uma solução para a desigualdade\(x+y>4\):
- \((6,1)\)
- \((−3,6)\)
- \((3,2)\)
- \((−5,10)\)
- \((0,0)\)
- Responda
-
- sim
- não
- sim
- sim
- não
Reconhecer a relação entre as soluções de uma desigualdade e seu gráfico
Nos exercícios a seguir, escreva a desigualdade mostrada pela região sombreada.
Escreva a desigualdade mostrada pelo gráfico com a linha limite\(y=−x+2\).
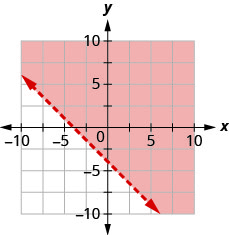
Escreva a desigualdade mostrada pelo gráfico com a linha limite\(y=\frac{2}{3} x-3\)
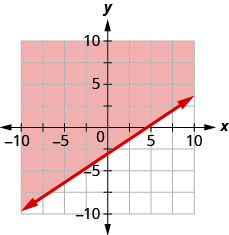
- Responda
-
\(y>\frac{2}{3} x-3\)
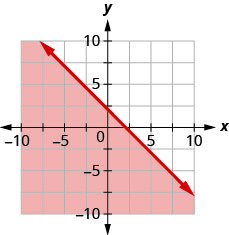
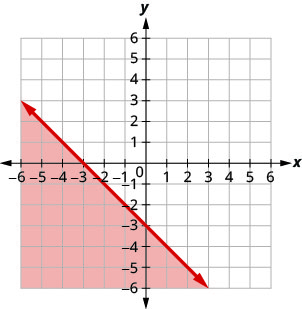
Escreva a desigualdade mostrada pela região sombreada no gráfico com a linha limite\(x+y=−4\).
Escreva a desigualdade mostrada pela região sombreada no gráfico com a linha limite\(x−2y=6\).
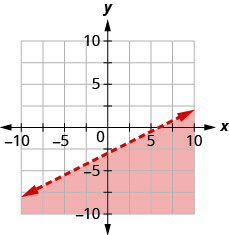
- Responda
-
\(x-2 y \geq 6\)
Gráfico de desigualdades lineares
Nos exercícios a seguir, represente graficamente cada desigualdade linear.
Representar graficamente a desigualdade linear\(y>\frac{2}{5} x-4\)
Representar graficamente a desigualdade linear\(y \leq-\frac{1}{4} x+3\)
- Responda
-
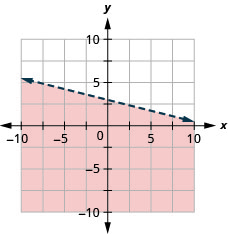
Representar graficamente a desigualdade linear\(x-y \leq 5\)
Representar graficamente a desigualdade linear\(3 x+2 y>10\)
- Responda
-
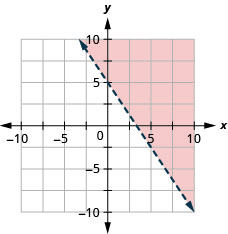
Representar graficamente a desigualdade linear\(y \leq-3 x\)
Representar graficamente a desigualdade linear\(y<6\)
- Responda
-
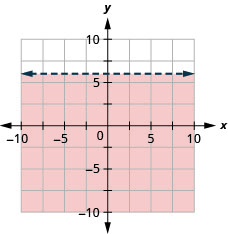
Teste prático
Faça um gráfico de cada ponto em um sistema de coordenadas retangular.
- \((2,5)\)
- \((−1,−3)\)
- \((0,2)\)
- \(\left(-4, \frac{3}{2}\right)\)
- \((5,0)\)
Quais dos pares ordenados fornecidos são soluções para a equação\(3x−y=6\)?
- \((3,3)\)
- \((2,0)\)
- \((4,−6)\)
- Responda
-
- sim
- sim
- não
Encontre três soluções para a equação linear\(y=-2x-4\)
Encontre os\(y\) interceptos\(x\) - e -da equação\(4x-3y=12\)
- Responda
-
\((3,0),(0,-4)\)
Encontre a inclinação de cada linha mostrada.
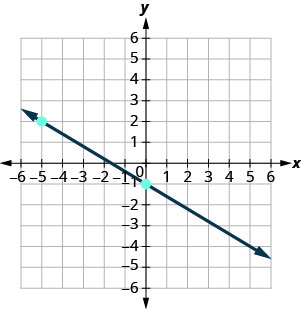
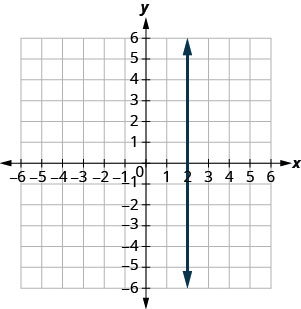
- Responda
-
indefinida
Encontre a inclinação da linha entre os pontos\((5,2)\) e\((-1,-4)\)
- Responda
-
1
Faça um gráfico da linha com inclinação\(\frac{1}{2}\) contendo o ponto\((-3,-4)\)
Faça um gráfico da linha para cada uma das equações a seguir.
\(y=\frac{5}{3} x-1\)
- Responda
-
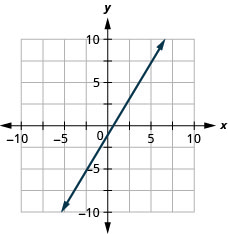
\(y=-x\)
\(x-y=2\)
- Responda
-
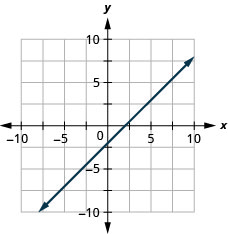
\(4x+2y=-8\)
\(y=2\)
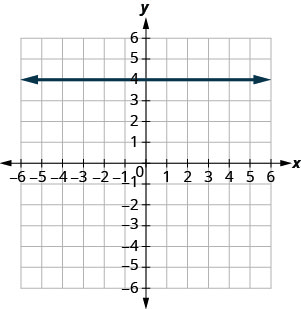
- Responda
-
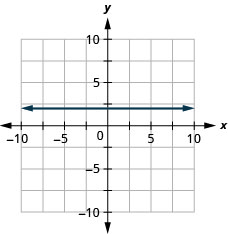
\(x=-3\)
Encontre a equação de cada linha. Escreva a equação na forma inclinação-interceptação.
inclinação\(-\frac{3}{4}\) e\(y\) interceptação\((0,-2)\)
- Responda
-
\(y=-\frac{3}{4} x-2\)
\(m=2,\)ponto\((-3,-1)\)
contendo\((10,1)\) e\((6,-1)\)
- Responda
-
\(y=\frac{1}{2} x-4\)
paralelo à linha\(y=-\frac{2}{3} x-1,\) que contém o ponto\((-3,8)\)
perpendicular à linha\(y=\frac{5}{4} x+2,\) que contém o ponto\((-10,3)\)
- Responda
-
\(y=-\frac{4}{5} x-5\)
Escreva a desigualdade mostrada pelo gráfico com a linha limite\(y=−x−3\).
Representar graficamente cada desigualdade linear.
\(y>\frac{3}{2} x+5\)
- Responda
-
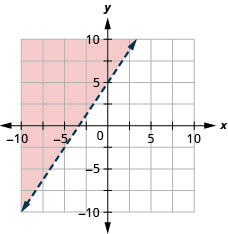
\(x-y \geq-4\)
\(y \leq-5 x\)
- Responda
-
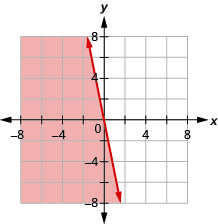
\(y<3\)