Skip to main content
Global

4.3: Gráfico com interceptações

  1. Last updated
  2. Save as PDF
  • Page ID
    184256

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    objetivos de aprendizagem

    Ao final desta seção, você poderá:

    • Identifique as interceptações x e y em um gráfico
    • Encontre as interceptações x e y de uma equação de uma reta
    • Faça um gráfico de uma linha usando as interceptações
    Nota

    Antes de começar, faça este teste de prontidão.

    1. Resolver:\(3\cdot 0+4y=−2\).
      Se você perdeu esse problema, revise o Exercício 2.2.13.

    Identifique as interceptações x e y em um gráfico

    Cada equação linear pode ser representada por uma linha única que mostra todas as soluções da equação. Vimos que, ao representar graficamente uma linha traçando pontos, você pode usar quaisquer três soluções para representar graficamente. Isso significa que duas pessoas representando graficamente a linha podem usar conjuntos diferentes de três pontos.

    À primeira vista, suas duas linhas podem não parecer iguais, pois teriam pontos diferentes rotulados. Mas se todo o trabalho foi feito corretamente, as linhas devem ser exatamente as mesmas. Uma forma de reconhecer que eles são realmente a mesma linha é observar onde a linha cruza o eixo x e o eixo y. Esses pontos são chamados de interceptações da linha.

    INTERCEPTAÇÕES DE UMA LINHA

    Os pontos em que uma linha cruza o eixo x e o eixo y são chamados de interceptações de uma linha.

    Vejamos os gráficos das linhas na Figura\(\PageIndex{1}\).

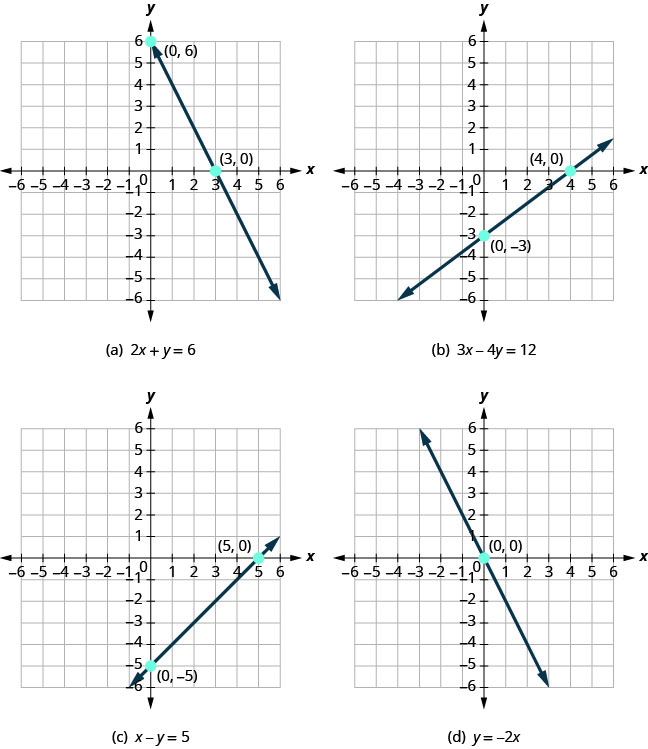
    Quatro figuras, cada uma mostrando uma linha reta diferente no plano de coordenadas x y. O eixo x dos planos vai de menos 7 a 7. O eixo y dos planos vai de menos 7 a 7. A Figura a mostra uma linha reta cruzando o eixo x no ponto (3, 0) e cruzando o eixo y no ponto (0, 6). O gráfico é rotulado com a equação 2x mais y igual a 6. A Figura b mostra uma linha reta cruzando o eixo x no ponto (4, 0) e cruzando o eixo y no ponto (0, menos 3). O gráfico é rotulado com a equação 3x menos 4y é igual a 12. A Figura c mostra uma linha reta cruzando o eixo x no ponto (5, 0) e cruzando o eixo y no ponto (0, menos 5). O gráfico é rotulado com a equação x menos y igual a 5. A Figura d mostra uma linha reta cruzando os eixos x e y no ponto (0, 0). O gráfico é rotulado com a equação y igual a menos 2x.
    Figura\(\PageIndex{1}\): Exemplos de gráficos cruzando o eixo x-negativo.

    Primeiro, observe onde cada uma dessas linhas cruza o eixo x negativo. Veja a Figura\(\PageIndex{1}\).

    Tabela\(\PageIndex{1}\)
    Figura A linha cruza o eixo x em: Par ordenado deste ponto
    Figura (a) 3 (3,0)
    Figura (b) 4 (4,0)
    Figura (c) 5 (5,0)
    Figura (d) 0 (0,0)

    Você vê um padrão?

    Para cada linha, a coordenada y do ponto em que a linha cruza o eixo x é zero. O ponto em que a linha cruza o eixo x tem a forma (a,0) e é chamado de intercepto x de uma linha. O intercepto x ocorre quando y é zero. Agora, vamos ver os pontos em que essas linhas cruzam o eixo y. Veja a tabela\(\PageIndex{2}\).

    Tabela\(\PageIndex{2}\)
    Figura A linha cruza o eixo x em: Par ordenado deste ponto
    Figura (a) 6 (0,6)
    Figura (b) −3 (0, −3)
    Figura (c) −5 (0,5)
    Figura (d) 0 (0,0)

    Qual é o padrão aqui?

    Em cada linha, a coordenada x do ponto em que a linha cruza o eixo y é zero. O ponto em que a linha cruza o eixo y tem a forma (0, b) e é chamado de intercepto y da linha. A intercepção y ocorre quando x é zero.

    INTERCEPTAÇÃO X E INTERCEPTAÇÃO Y DE UMA LINHA

    O intercepto x é o ponto (a,0) em que a linha cruza o eixo x.

    O intercepto y é o ponto (0, b) em que a linha cruza o eixo y.

    Sem texto alternativo
    Figura\(\PageIndex{2}\)
    Exercício\(\PageIndex{1}\)

    Encontre as interceptações x e y em cada gráfico.

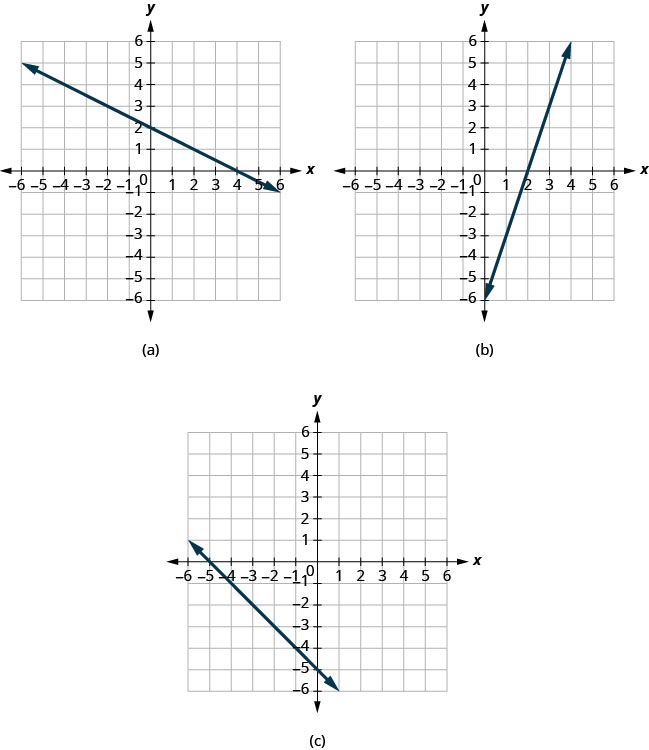
    Três figuras, cada uma mostrando uma linha reta diferente no plano de coordenadas x y. O eixo x dos planos vai de menos 7 a 7. O eixo y dos planos vai de menos 7 a 7. A Figura a mostra uma linha reta passando pelos pontos (menos 6, 5), (menos 4, 4), (menos 2, 3), (0, 2), (2, 1), (4, 0) e (6, menos 1). A Figura b mostra uma linha reta passando pelos pontos (0, menos 6), (1, menos 3), (2, 0), (3, 3) e (4, 6). A Figura c mostra uma linha reta passando pelos pontos (menos 6, 1), (menos 5, 0), (menos 4, menos 1), (menos 3, menos 2), (menos 2, menos 3), (negativo 1, negativo 4), (0, menos 5) e (1, menos 6).
    Figura\(\PageIndex{3}\)
    Responda

    (a) O gráfico cruza o eixo x no ponto (4,0). O intercepto x é (4,0).
    O gráfico cruza o eixo y no ponto (0,2). O intercepto y é (0,2).

    (b) O gráfico cruza o eixo x no ponto (2,0). O intercepto x é (2,0)
    O gráfico cruza o eixo y no ponto (0, −6). O intercepto y é (0, −6).

    (c) O gráfico cruza o eixo x no ponto (−5,0). O intercepto x é (−5,0).
    O gráfico cruza o eixo y no ponto (0, −5). O intercepto y é (0, −5).

    Exercício\(\PageIndex{2}\)

    Encontre as interceptações x e y no gráfico.

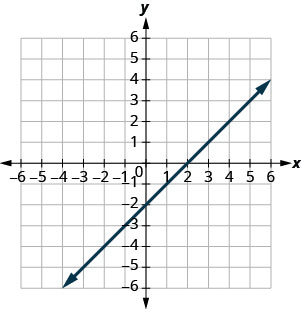
    Uma figura mostrando uma linha reta no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y dos planos vai de menos 10 a 10. A linha reta passa pelos pontos (menos 8, menos 10), (menos 6, menos 8), (menos 4, menos 6), (menos 2, menos 4), (0, menos 2), (2, 0), (4, 2), (6, 4), (8, 6) e (10, 8) e (10, 8).

    Responda

    x - interceptar: (2,0); y - interceptar: (0, −2)

    Exercício\(\PageIndex{3}\)

    Encontre as interceptações x e y no gráfico.

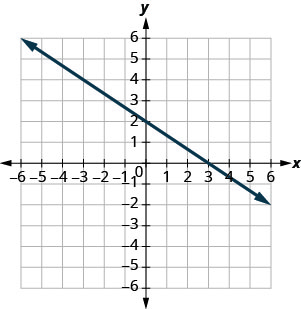
    A figura mostra uma linha reta no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y dos planos vai de menos 10 a 10. A linha reta passa pelos pontos (menos 9, 8), (menos 6, 6), (menos 3, 4), (0, 2), (3, 0), (6, menos 2) e (9, menos 4).

    Responda

    x - interceptar: (3,0), y - interceptar: (0,2)

    Encontre as interceptações x e y de uma equação de uma reta

    Reconhecer que a interceptação x ocorre quando y é zero e que a interceptação y ocorre quando x é zero, nos dá um método para encontrar as interceptações de uma linha a partir de sua equação. Para encontrar o intercepto x, deixe y = 0 e resolva para x. Para encontrar a interceptação y, deixe x=0 e resolva por y.

    X- E Y - INTERCEPTAÇÕES DA EQUAÇÃO DE UMA RETA

    Use a equação da linha. Para encontrar:

    • o x - intercepte a linha, deixe y = 0 e resolva para x.
    • o y - intercepte a linha, deixe x=0 e resolva por y.
    Exercício\(\PageIndex{4}\)

    Encontre as interceptações de 2x+y=6.

    Responda

    Vamos deixar que y=0 encontre a interceptação x e deixaremos que x=0 encontre a interceptação y. Vamos preencher a tabela, o que nos lembra do que precisamos encontrar.

    A figura mostra uma tabela com quatro linhas e duas colunas. A primeira linha é uma linha de título e ela rotula a tabela com a equação 2 x mais y é igual a 6. A segunda linha é uma linha de cabeçalho e rotula cada coluna. O cabeçalho da primeira coluna é “x” e o segundo é “y”. A terceira linha é rotulada como “x- intercept” e tem a primeira coluna em branco e um 0 na segunda coluna. A quarta linha é rotulada como “intercepto y” e tem um 0 na primeira coluna com a segunda coluna em branco.

    Para encontrar o intercepto x, deixe y=0.

    Tabela\(\PageIndex{3}\)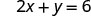
      .
    Seja y = 0. .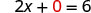
    Simplifique. .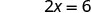
      .
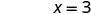
    O intercepto x é (3, 0)
    Para encontrar o intercepto y, deixe x = 0.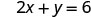  
      .
    Seja x = 0. .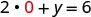
    Simplifique. .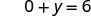
      .
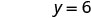
    O intercepto y é (0, 6)
    As interceptações são os pontos (3,0) e (0,6) conforme mostrado na Tabela\(\PageIndex{4}\).
    Tabela\(\PageIndex{4}\)
    2x+y=6
    x y
    3 0
    0 6
    Exercício\(\PageIndex{5}\)

    Encontre as interceptações de 3x+y=12.

    Responda

    x - interceptar: (4,0), y - interceptar: (0,12)

    Exercício\(\PageIndex{6}\)

    Encontre as interceptações de x+4y=8.

    Responda

    x - interceptar: (8,0), y - interceptar: (0,2)

    Exercício\(\PageIndex{7}\)

    Encontre as interceptações de 4x—3y=12.

    Responda
    Para encontrar o intercepto x, deixe y = 0.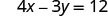  
      .
    Seja y = 0. .
    Simplifique. .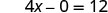
      .
      .
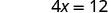
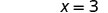
    O intercepto x é (3, 0)
    Para encontrar o intercepto y, deixe x = 0.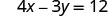  
      .
    Seja x = 0. .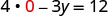
    Simplifique. .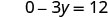
      .
      .
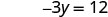
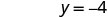
    O intercepto y é (0, −4)
    Tabela\(\PageIndex{5}\)

    Os interceptos são os pontos (3, 0) e (0, −4), conforme mostrado na tabela a seguir.

    Tabela\(\PageIndex{6}\)
    4x−3y=12
    x y
    3 0
    0 −4
    Exercício\(\PageIndex{8}\)

    Encontre as interceptações de 3x—4y=12.

    Responda

    x - interceptar: (4,0), y - interceptar: (0, −3)

    Exercício\(\PageIndex{9}\)

    Encontre as interceptações de 2x—4y=8.

    Responda

    x - interceptar: (4,0), y - interceptar: (0, −2)

    Faça um gráfico de uma linha usando as interceptações

    Para representar graficamente uma equação linear traçando pontos, você precisa encontrar três pontos cujas coordenadas são soluções para a equação. Você pode usar as interceptações x e y como dois dos seus três pontos. Encontre as interceptações e, em seguida, encontre um terceiro ponto para garantir a precisão. Certifique-se de que os pontos estejam alinhados e, em seguida, desenhe a linha. Esse método geralmente é a maneira mais rápida de representar graficamente uma linha.

    Exercício\(\PageIndex{10}\): How to Graph a Line Using Intercepts

    Faça um gráfico de —x+2y=6 usando as interceptações.

    Responda

    A figura mostra uma tabela com o procedimento geral para representar graficamente uma linha usando os interceptos junto com um exemplo específico usando a equação menos x mais 2y é igual a 6. A etapa 1 do procedimento geral é “Encontre as interceptações x e y da linha. Seja y igual a 0 e resolva por x. Seja x igual a 0 e resolva por y”. A etapa 1 do exemplo é uma série de afirmações e equações: “Encontre o intercepto x. Seja y igual a 0”, menos x mais 2y é igual a 6, menos x mais 2 (0) é igual a 6 (onde o 0 é vermelho), menos x é igual a 6, x é igual a menos 6, “O intercepto x é (menos 6, 0)”, “Encontre o intercepto y. Seja x igual a 0”, menos x mais 2y é igual a 6, menos 0 mais 2y é igual a 6 (onde o 0 é vermelho), 2y é igual a 6, y é igual a 3 e “O intercepto y é (0, 3)”.A etapa 2 do procedimento geral é “Encontre outra solução para a equação”. A etapa 2 do exemplo é uma série de afirmações e equações: “Usaremos x igual a 2”, “Seja x igual a 2”, menos x mais 2y é igual a 6, menos 2 mais 2y é igual a 6 (onde o primeiro 2 é vermelho), 2y é igual a 8, y é igual a 4 e “Um terceiro ponto é (2, 4)”. A etapa 3 do procedimento geral é “Traçar os três pontos. 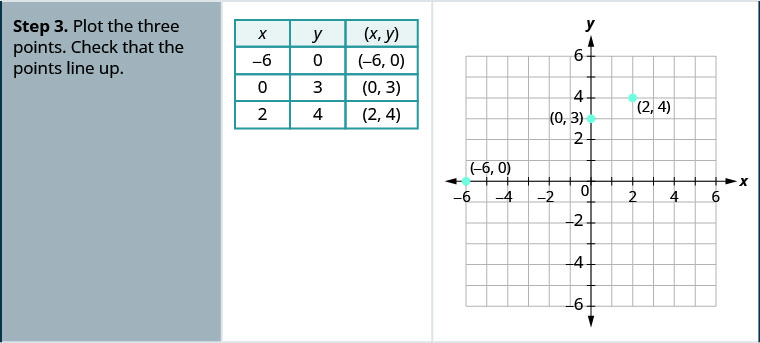Verifique se os pontos estão alinhados.”A etapa 3 do exemplo é uma tabela e um gráfico. A tabela tem quatro linhas e três colunas. A primeira linha é uma linha de cabeçalho e rotula cada coluna. O cabeçalho da primeira coluna é “x”, o segundo é “y” e o terceiro é “(x, y)”. Sob a primeira coluna estão os números negativos 6, 0 e 2. Sob a segunda coluna estão os números 0, 3 e 4. Abaixo da terceira coluna estão os pares ordenados (menos 6, 0), (0, 3) e (2, 4). O gráfico tem três pontos no plano de coordenadas x- y. O eixo x do plano vai de menos 7 a 7. O eixo y dos planos vai de menos 7 a 7. 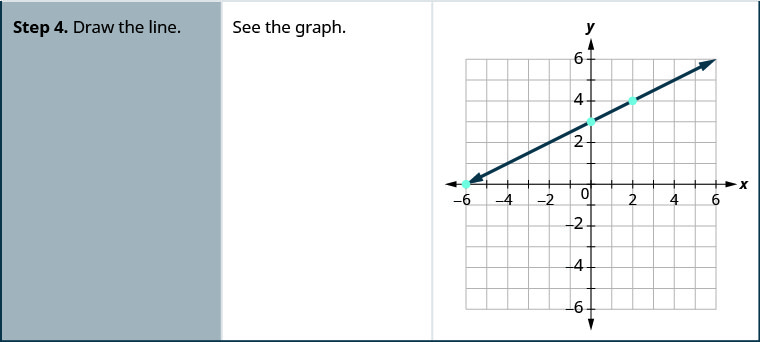Três pontos são marcados em (menos 6, 0), (0, 3) e (2, 4).A etapa 4 do procedimento geral é “Desenhar a linha”. Para o exemplo específico, há a declaração “Veja o gráfico” e um gráfico de uma linha reta passando por três pontos no plano de coordenadas x y. O eixo x do plano vai de menos 7 a 7. O eixo y dos planos vai de menos 7 a 7. Três pontos são marcados em (menos 6, 0), (0, 3) e (2, 4). A linha reta é traçada através dos pontos (menos 6, 0), (menos 4, 1), (menos 2, 2), (0, 3), (2, 4), (4, 5) e (6, 6).

    Exercício\(\PageIndex{11}\)

    Gráfico x—2y=4 usando os interceptos.

    Responda

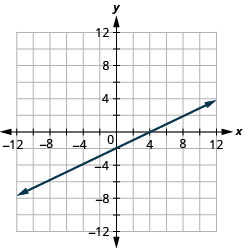
    A figura mostra uma linha reta no plano de coordenadas x y. O eixo x do plano vai de menos 12 a 12. O eixo y dos planos vai de menos 12 a 12. A linha reta passa pelos pontos (menos 10, menos 7), (menos 8, menos 6), (menos 6, menos 5), (menos 4, menos 4), (menos 2, menos 3), (0, menos 2), (2, menos 1), (4, 0), (6, 1), (8, 2) e (10, 3).

    Exercício\(\PageIndex{12}\)

    Faça um gráfico de —x+3y=6 usando as interceptações.

    Responda

    A figura mostra uma linha reta no plano de coordenadas x y. O eixo x do plano vai de menos 12 a 12. O eixo y dos planos vai de menos 12 a 12. A linha reta passa pelos pontos (menos 12, menos 2), (menos 9, menos 1), (menos 6, 0), (menos 3, 1), (0, 2), (3, 3), (6, 4), (9, 5) e (12, 6).

    As etapas para representar graficamente uma equação linear usando os interceptos estão resumidas abaixo.

    FAÇA UM GRÁFICO DE UMA EQUAÇÃO LINEAR USANDO AS INTERCEPTAÇÕES
    1. Encontre as interceptações x e y da linha.
      • Seja y = 0 e resolva para x
      • Seja x = 0 e resolva por y.
    2. Encontre uma terceira solução para a equação.
    3. Faça um gráfico dos três pontos e verifique se eles estão alinhados.
    4. Desenhe a linha.
    Exercício\(\PageIndex{13}\)

    Gráfico 4x—3y=12 usando os interceptos.

    Responda

    Encontre as interceptações e um terceiro ponto.

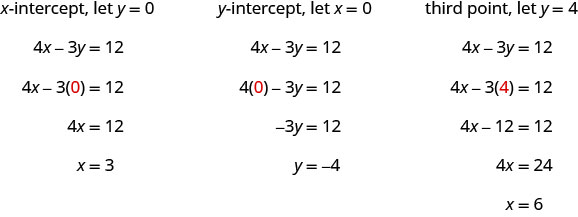
    A figura mostra uma série de afirmações e equações: “Encontre o intercepto x. Seja y igual a 0”, 4x menos 3y é igual a 12, 4x menos 3 (0) é igual a 12 (onde o 0 é vermelho), 4x é igual a 12, x é igual a 3, “Encontre o intercepto y. Seja x igual a 0”, 4x menos 3y é igual a 12, 4 (0) menos 3y é igual a 12 (onde o 0 é vermelho), menos 3y é igual a 12, y é igual a menos 4, “terceiro ponto, seja y igual a 4”, 4x menos 3y é igual a 12, 4x menos 3 (4) é igual a 12 (onde o segundo 4 é vermelho), 4x menos 12 é igual a 12, 4x é igual a 24 e x é igual a 6.

    Listamos os pontos na Tabela\(\PageIndex{7}\) e mostramos o gráfico abaixo.

    4x−3y=12
    x y (x, y)
    3 0 (3,0)
    0 −4 (0, −4)
    6 4 (6,4)
    Tabela\(\PageIndex{7}\)

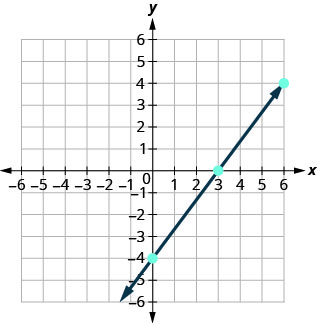
    A figura mostra o gráfico de uma linha reta passando por três pontos no plano de coordenadas x y. O eixo x do plano vai de menos 7 a 7. O eixo y dos planos vai de menos 7 a 7. Três pontos são marcados em (0, menos 4), (3, 0) e (6, 4). A linha reta é traçada através dos pontos (0, menos 4), (3, 0) e (6, 4).

    Exercício\(\PageIndex{14}\)

    Gráfico 5x—2y=10 usando os interceptos.

    Responda

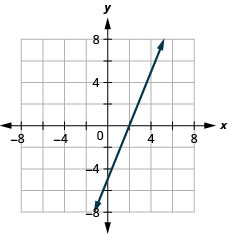
    A figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x do plano vai de menos 7 a 7. O eixo y dos planos vai de menos 7 a 7. A linha reta passa pelos pontos (0, menos 5), (2, 0) e (4, 5).

    Exercício\(\PageIndex{15}\)

    Gráfico 3x—4y=12 usando os interceptos.

    Responda

    A figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x do plano vai de menos 7 a 7. O eixo y dos planos vai de menos 7 a 7. A linha reta passa pelos pontos (menos 4, menos 6), (0, menos 3) e (4, 0).

    Exercício\(\PageIndex{16}\)

    Grafe y=5x usando os interceptos.

    Responda

    A figura mostra dois conjuntos de declarações e equações para encontrar os interceptos de uma equação. O primeiro conjunto de declarações e equações é “x- interceptar”, “deixe y ser igual a 0”, y é igual a 5x, 0 é igual a 5x (onde o 0 é vermelho), 0 é igual a x, (0, 0). O segundo conjunto de declarações e equações é “interceptar y”, “deixe x igual a 0”, y é igual a 5x, y é igual a 5 (0) (onde o 0 é vermelho), y é igual a 0, (0, 0).

    Essa linha tem apenas uma interceptação. É o ponto (0,0).

    Para garantir a precisão, precisamos traçar três pontos. Como as interceptações x e y são o mesmo ponto, precisamos de mais dois pontos para representar graficamente a linha.

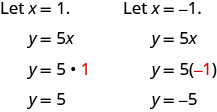
    A figura mostra dois conjuntos de declarações e equações para encontrar dois pontos de uma equação. O primeiro conjunto de declarações e equações é “Seja x igual a 1”, y é igual a 5x, y é igual a 5 (1) (onde o 1 é vermelho), y é igual a 5. O segundo conjunto de declarações e equações é “Seja x igual a menos 1”, y é igual a 5x, y é igual a 5 (menos 1) (onde o negativo 1 é vermelho), y é igual a menos 5.

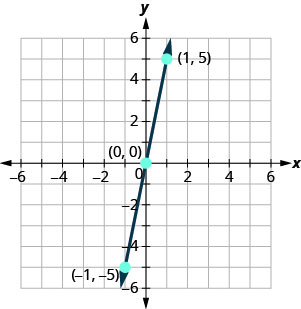
    Veja a tabela\(\PageIndex{8}\).

    y = 5x
    x y (x, y)
        (0,0)
        (1,5)
    −1 −5 (−1, −5)
    Tabela\(\PageIndex{8}\)

    Faça um gráfico dos três pontos, verifique se eles estão alinhados e desenhe a linha.

    A figura mostra o gráfico de uma linha reta passando por três pontos no plano de coordenadas x y. O eixo x do plano vai de menos 10 a 10. O eixo y dos planos vai de menos 10 a 10. Três pontos são marcados e rotulados com suas coordenadas em (menos 1, menos 5), (0, 0) e (1, 5). A linha reta é traçada através dos pontos (menos 1, menos 5), (0, 0) e (1, 5).

    Exercício\(\PageIndex{17}\)

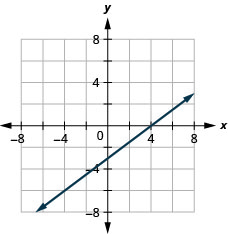
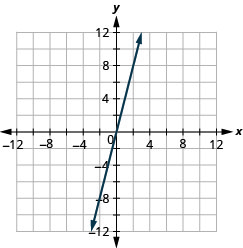
    Faça um gráfico de y=4x usando os interceptos.

    Responda

    A figura mostra uma linha reta no plano de coordenadas x y. O eixo x do plano vai de menos 12 a 12. O eixo y dos planos vai de menos 12 a 12. A linha reta passa pelos pontos (menos 4, menos 12), (menos 3, menos 9), (menos 2, menos 6), (menos 1, menos 3), (0, 0), (1, 3), (2, 6), (3, 9) e (4, 12).

    Exercício\(\PageIndex{18}\)

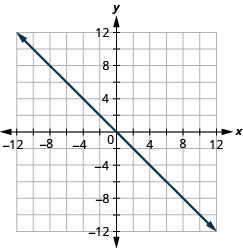
    Representa graficamente y=−x as interceptações.

    Responda

    A figura mostra uma linha reta no plano de coordenadas x y. O eixo x do plano vai de menos 12 a 12. O eixo y dos planos vai de menos 12 a 12. A linha reta passa pelos pontos (menos 10, 10), (menos 9, 9), (menos 8, 8), (menos 7, 7), (menos 6, 6), (menos 5, 5), (menos 4, 4), (menos 3, 3), (menos 2, 2), (menos 1, 1), (0, 0), (1, negativo 1), (2, menos 2), (3, menos 3), (4, menos 4), (5, menos 5), (6, menos 6), (7, menos 7), (8, menos 8), (9, menos 9) e (10, menos 10).

    Conceitos chave

    • Encontre as interceptações x e y da equação de uma reta
      • Use a equação da linha para encontrar o x - intercepto da linha, deixe y = 0 e resolva x.
      • Use a equação da linha para encontrar o intercepto y da linha, deixe x=0 e resolva por y.
    • Representar graficamente uma equação linear usando os interceptos
      1. Encontre as interceptações x e y da linha.
        Deixe y = 0 e resolva para x.
        Seja x = 0 e resolva por y.
      2. Encontre uma terceira solução para a equação.
      3. Faça um gráfico dos três pontos e verifique se eles estão alinhados.
      4. Desenhe a linha.
    • Estratégia para escolher o método mais conveniente para representar graficamente uma linha:
      • Considere a forma da equação.
      • Se tiver apenas uma variável, é uma linha vertical ou horizontal.
        x=a é uma linha vertical passando pelo eixo x em a
        y=b é uma linha horizontal passando pelo eixo y em b.
      • Se y estiver isolado em um lado da equação, represente graficamente pontos.
      • Escolha quaisquer três valores para x e, em seguida, resolva para os valores y correspondentes.
      • Se a equação for da forma ax+by=c, encontre os interceptos. Encontre as interceptações x e y e depois um terceiro ponto.

    Glossário

    interceptações de uma linha
    Os pontos em que uma linha cruza o eixo x e o eixo y são chamados de interceptações da linha.
    x - interceptar
    O ponto (a,0) em que a linha cruza o eixo x; o intercepto x ocorre quando y é zero.
    y -intercept
    O ponto (0, b) em que a linha cruza o eixo y; a interceptação y ocorre quando x é zero.