2.6: Resolver uma fórmula para uma variável específica
- Page ID
- 184173
Ao final desta seção, você poderá:
- Use a fórmula de Distância, Taxa e Tempo
- Resolver uma fórmula para uma variável específica
Antes de começar, faça este teste de prontidão.
- Resolver:\(15t=120\).
Se você perdeu esse problema, revise o Exercício 2.2.1. - Resolver:\(6x+24=96\).
Se você perdeu esse problema, revise o Exercício 2.3.1.
Use a fórmula de distância, taxa e tempo
Uma fórmula que você usará frequentemente em álgebra e na vida cotidiana é a fórmula para a distância percorrida por um objeto que se move a uma taxa constante. Taxa é uma palavra equivalente para “velocidade”. A ideia básica de tarifa pode já ser familiar para você. Você sabe qual distância percorre se dirigir a uma taxa constante de 60 milhas por hora por 2 horas? (Isso pode acontecer se você usar o controle de cruzeiro do seu carro enquanto dirige na rodovia.) Se você disse 120 milhas, você já sabe como usar essa fórmula!
Para um objeto que se move a uma taxa uniforme (constante), a distância percorrida, o tempo decorrido e a taxa são relacionados pela fórmula:
\[\begin{array} {lllll}{ d = r t} &{\text { where }} &{ d} &{=} &{\text{distance}} \\ {} &{} &{ r} &{=} &{\text{rate}} \\{} &{} &{ t} &{=} &{\text{time}} \end{array}\]
Usaremos a estratégia para resolver aplicativos que usamos anteriormente neste capítulo. Quando nosso problema exige uma fórmula, mudamos a Etapa 4. Em vez de escrever uma frase, escrevemos a fórmula apropriada. Escrevemos as etapas revisadas aqui para referência.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Traduza em uma equação. Escreva a fórmula apropriada para a situação. Substitua as informações fornecidas.
- Resolva a equação usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
Talvez você queira criar um mini-gráfico para resumir as informações do problema. Veja o gráfico neste primeiro exemplo.
Jamal anda de bicicleta a uma taxa uniforme de 12 milhas por hora durante\(3\frac{1}{2}\) horas. Que distância ele percorreu?
- Resposta
-
Etapa 1. Leia o problema. Etapa 2. Identifique o que você está procurando. distância percorrida Etapa 3. Nome. Escolha uma variável para representá-la. Seja d = distância. Etapa 4. Traduzir: escreva a fórmula apropriada. \(d=rt\) 
Substitua as informações fornecidas. \(d = 12\cdot 3\frac{1}{2}\) Etapa 5. Resolva a equação. \(d=42\text{ miles}\) Etapa 6. Verifique 42 milhas fazem sentido? Jamal monta: 
Etapa 7. Responda à pergunta com uma frase completa. Jamal andou 42 milhas.
Lindsay dirigiu por\(5\frac{1}{2}\) horas a 60 milhas por hora. Quanta distância ela percorreu?
- Resposta
-
330 milhas
Trinh caminhou por\(2\frac{1}{3}\) horas a 3 milhas por hora. Até onde ela andou?
- Resposta
-
7 milhas
Rey planeja ir de carro de sua casa em San Diego para visitar sua avó em Sacramento, a uma distância de 520 milhas. Se ele puder dirigir a uma taxa constante de 65 milhas por hora, quantas horas a viagem levará?
- Resposta
-
Etapa 1. Leia o problema. Etapa 2. Identifique o que você está procurando. Quantas horas (hora) Etapa 3. Nome.
Escolha uma variável para representá-la.Deixe t = tempo. 
Etapa 4. Traduzir.
Escreva a fórmula apropriada.\(d=rt\) Substitua as informações fornecidas. \(520 = 65t\) Etapa 5. Resolva a equação. \(t = 8\) Etapa 6. Verifique. Substitua os números
na fórmula e certifique-se de que o resultado seja uma afirmação
verdadeira.\(\begin{array}{lll} {d} &{=} &{rt} \\ {520} &{\stackrel{?}{=}} &{65\cdot 8}\\ {520} &{=} &{520\checkmark} \end{array}\) Etapa 7. Responda à pergunta com uma frase completa. A viagem de Rey levará 8 horas.
Lee quer dirigir de Phoenix até o apartamento de seu irmão em San Francisco, a uma distância de 770 milhas. Se ele dirigir a uma taxa constante de 70 milhas por hora, quantas horas a viagem levará?
- Resposta
-
11 horas
Yesenia fica a 270 km de Chicago. Se ela precisar estar em Chicago em 3 horas, a que ritmo ela precisa dirigir?
- Resposta
-
56 mph
Resolver uma fórmula para uma variável específica
Você provavelmente está familiarizado com algumas fórmulas de geometria. Uma fórmula é uma descrição matemática da relação entre as variáveis. As fórmulas também são usadas nas ciências, como química, física e biologia. Na medicina, eles são usados para cálculos para dispensar medicamentos ou determinar o índice de massa corporal. Os programas de planilhas dependem de fórmulas para fazer cálculos. É importante estar familiarizado com as fórmulas e ser capaz de manipulá-las facilmente.
Em Exercício\(\PageIndex{1}\) e Exercício\(\PageIndex{4}\), usamos a fórmula\(d=rt\). Essa fórmula fornece o valor de d, distância, quando você substitui os valores de r e t, a taxa e o tempo. Mas no Exercício\(\PageIndex{4}\), tivemos que encontrar o valor de t. Substituímos os valores de d e r e depois usamos a álgebra para resolver tt. Se você tivesse que fazer isso com frequência, talvez se perguntasse por que não existe uma fórmula que forneça o valor de t quando você substitui os valores de d e r. Podemos criar uma fórmula como essa resolvendo a fórmula\(d=rt\) para t.
Resolver uma fórmula para uma variável específica significa isolar essa variável em um lado do sinal de igual com um coeficiente de 1. Todas as outras variáveis e constantes estão do outro lado do sinal de igual. Para ver como resolver uma fórmula para uma variável específica, começaremos com a fórmula de distância, taxa e tempo.
Resolva a fórmula d=rt para t:
- quando d=520 e r=65
- em geral
- Resposta
-
Escreveremos as soluções lado a lado para demonstrar que a resolução de uma fórmula em geral usa as mesmas etapas de quando temos números para substituir.
1. quando d=520 e r=65 2. em geral Escreva a fórmula. \(d=rt\) Escreva a fórmula. \(d=rt\) Substituto. \(520=65t\) Divida, para isolar t. \(\frac{520}{65} = \frac{65t}{65}\) Divida, para isolar tt. \(\frac{d}{r} = \frac{rt}{t}\) Simplifique. \(8 = t\) Simplifique. \(\frac{d}{r}=t\) Dizemos que a fórmula\(t = \frac{d}{r}\) está resolvida para t.
Resolva a fórmula\(d=rt\) para r:
- quando d=180 e t=4
- em geral
- Resposta
-
- \(r = 45\)
- \(r = \frac{d}{t}\)
Resolva a fórmula\(d=rt\) para r:
- quando d=780 e t=12
- em geral
- Resposta
-
- \(r = 65\)
- \(r = \frac{d}{rt\)
Resolva a fórmula\(A = \frac{1}{2}bh\) para h:
- quando\(A = 90\) e\(b = 15\)
- em geral
- Resposta
-
Agora podemos encontrar a altura de um triângulo, se soubermos a área e a base, usando a fórmula\(h = \frac{2A}{b}\)1. quando\(A = 90\) e\(b = 15\) 2. em geral Escreva a fórmula. 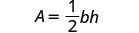
Escreva a fórmula. 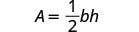
Substituto. 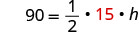
Limpe as frações. 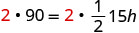
Limpe as frações. 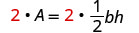
Simplifique. 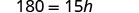
Simplifique. 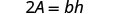
Resolva para h. 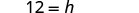
Resolva para hh. 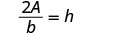
Resolva a fórmula\(A = \frac{1}{2}bh\) para h:
- quando\(A = 170\) e\(b = 17\)
- em geral
- Resposta
-
- \(h = 20\)
- \(h = \frac{2A}{b}\)
Resolva a fórmula\(A = \frac{1}{2}bh\) para h:
- quando\(A = 62\) e\(h = 31\)
- em geral
- Resposta
-
- \(b = 4\)
- \(b = \frac{2A}{h}\)
A fórmula\(I=Prt\) é usada para calcular juros simples, I, para um principal, P, investido à taxa, r, por t anos.
Resolva a fórmula I = Prt para encontrar o principal, P:
- quando I = $5.600, r = 4%, t = 7 anos
- em geral
- Resposta
-
1. I = $5.600, r = 4%, t = 7 anos 2. em geral Escreva a fórmula. 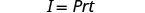
Escreva a fórmula. 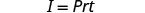
Substituto. 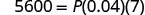
Simplifique. 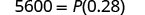
Simplifique. 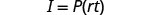
Divida, para isolar P. 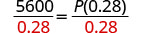
Divida, para isolar P. 
Simplifique. 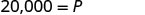
Simplifique. 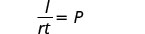
O diretor é 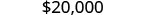
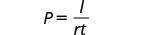
Resolva a fórmula I = Prt para encontrar o principal, P:
- quando I = $2160, r = 6%, t = 3 anos
- em geral
- Resposta
-
- $12.000
- \(P = \frac{1}{rt}\)
Resolva a fórmula I = Prt para encontrar o principal, P:
- quando I = $5400, r = 12%, t = 5 anos
- em geral
- Resposta
-
- $9000
- \(P = \frac{1}{rt}\)
Resolva a fórmula 3x+2y=18 para y:
- quando x=4
- em geral
- Resposta
-
1. quando x = 4 2. em geral 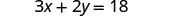
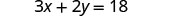
Substituto. 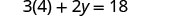
Subtraia para isolar o
termo y.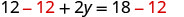
Subtraia para isolar o
termo y.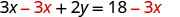
Divida. 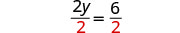
Divida. 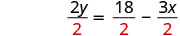
Simplifique. 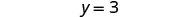
Simplifique. 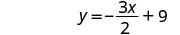
Resolva a fórmula 3x+4y=10 para y:
- quando\(x = \frac{14}{3}\)
- em geral
- Resposta
-
- \(y = -1\)
- \(y = \frac{10 - 3x}{4}\)
Resolva a fórmula 5x+2y=18 para y:
- quando\(x = 4\)
- em geral
- Resposta
-
- \(y = -1\)
- \(y = \frac{18 - 5x}{2}\)
Resolva a fórmula p=A+b+c para a.
- Resposta
-
Isolaremos aa em um lado da equação. 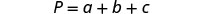
Tanto b quanto c são somados a a, então os subtraímos de ambos os lados da equação. 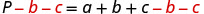
Simplifique. 
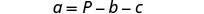
Resolva a fórmula p=A+b+c para b.
- Resposta
-
b=p−A−c
Resolva a fórmula p=A+b+c para c.
- Resposta
-
C=p−A−b
Resolva a fórmula 6x+5y=13 para y.
- Resposta
-
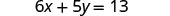
Subtraia 6x de ambos os lados para isolar o termo com y. 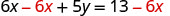
Simplifique. 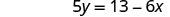
Divida por 5 para obter o coeficiente 1. 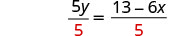
Simplifique. 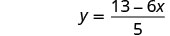
A fração é simplificada. Não podemos dividir 13−6x por 5.
Resolva a fórmula 4x+7y=9 para y.
- Resposta
-
\(y = \frac{9 - 4x}{7}\)
Resolva a fórmula 5x+8y=1 para y.
- Resposta
-
\(y = \frac{1 - 5x}{8}\)
Conceitos chave
- Para resolver um aplicativo (com uma fórmula)
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que estamos procurando.
- Diga o que estamos procurando. Escolha uma variável para representar essa quantidade.
- Traduza em uma equação. Escreva a fórmula apropriada para a situação. Substitua as informações fornecidas.
- Resolva a equação usando boas técnicas de álgebra.
- Verifique a resposta do problema e verifique se faz sentido.
- Responda à pergunta com uma frase completa.
- Distância, taxa e tempo
Para um objeto que se move a uma taxa uniforme (constante), a distância percorrida, o tempo decorrido e a taxa são relacionados pela fórmula: d=rt, onde d = distância, r = taxa, t = tempo. - Resolver uma fórmula para uma variável específica significa obter essa variável sozinha com um coeficiente de 1 em um lado da equação e todas as outras variáveis e constantes no outro lado.


