Skip to main content
Global

2.4: Use uma estratégia geral para resolver equações lineares

  1. Last updated
  2. Save as PDF
  • Page ID
    184190

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Resolva equações usando uma estratégia geral
    • Classifique equações
    Nota

    Antes de começar, faça este teste de prontidão.

    1. Simplifique:\(−(a−4)\).
      Se você perdeu esse problema, revise o Exercício 1.10.46
    2. Multiplicar:\(\frac{3}{2}(12x+20)\)
      Se você perdeu esse problema, revise o Exercício 1.10.34.
    3. Simplifique:\(5−2(n+1)\)
      se você perdeu esse problema, revise o Exercício 1.10.49.
    4. Multiplicar:\(3(7y+9)\)
      Se você perdeu esse problema, revise o Exercício 1.10.34.
    5. Multiplicar:\((2.5)(6.4)\)
      Se você perdeu esse problema, revise o Exercício 1.8.19.

    Resolva equações usando a estratégia geral

    Até agora, lidamos com a resolução de uma forma específica de uma equação linear. Agora é hora de traçar uma estratégia geral que possa ser usada para resolver qualquer equação linear. Algumas equações que resolvemos não precisarão de todas essas etapas para serem resolvidas, mas muitas o farão.

    Começar simplificando cada lado da equação facilita as etapas restantes.

    Exercício\(\PageIndex{1}\): How to Solve Linear Equations Using the General Strategy

    Resolver:\(-6(x + 3) = 24\).

    Resposta

    Essa figura é uma tabela que tem três colunas e cinco linhas. A primeira coluna é uma coluna de cabeçalho e contém os nomes e números de cada etapa. A segunda coluna contém mais instruções escritas. A terceira coluna contém matemática. Na linha superior da tabela, a primeira célula à esquerda diz: “Etapa 1. Simplifique cada lado da equação o máximo possível.” O texto na segunda célula diz: “Use a propriedade distributiva. Observe que cada lado da equação é simplificado o máximo possível.” A terceira célula contém a equação menos 6 vezes x mais 3, onde x mais 3 está entre parênteses, é igual a 24. Abaixo está a mesma equação com o menos 6 distribuído entre parênteses: menos 6x menos 18 é igual a 24.Etapa 2. Colete todos os termos variáveis em um lado da equação. Aqui não há mais nada a fazer, pois há apenas um x no lado esquerdo.Na terceira linha da tabela, a primeira célula diz: “Etapa 3. Colete termos constantes no outro lado da equação. Na segunda célula, as instruções dizem: “Para obter constantes apenas à direita, adicione 18 a cada lado. Simplifique.” A terceira célula contém a mesma equação com 18 adicionado aos dois lados: menos 6x menos 18 mais 18 é igual a 24 mais 18. Abaixo disso está a equação menos 6x igual a 42.Etapa 4. Faça o coeficiente de x um. Aqui dividimos os dois lados por -6 e simplificamos!Na quinta linha da tabela, a primeira célula diz: “Etapa 5. Verifique a solução.” Na segunda célula, as instruções dizem: “Seja x igual a menos 7. Simplifique. Multiplique.” Na terceira célula, há a instrução: “Verificar”, e à direita dela está a equação original novamente: menos 6 vezes x mais 3, com x mais 3 entre parênteses, igual a 24. Abaixo está a mesma equação com menos 7 substituído por x: menos 6 vezes menos 7 mais 3, com menos 7 mais 3 entre parênteses, pode ser igual a 24. Abaixo disso está a equação menos 6 vezes menos 4 pode ser igual a 24. Abaixo está a equação 24 é igual a 24, com uma marca de verificação ao lado.

    Exercício\(\PageIndex{2}\)

    Resolver:\(5(x + 3)=35\)

    Resposta

    \(x = 4\)

    Exercício\(\PageIndex{3}\)

    Resolver:\(6(y - 4) = -18\)

    Resposta

    \(y = 1\)

    ESTRATÉGIA GERAL PARA RESOLVER EQUAÇÕES LINEARES.
    1. Simplifique cada lado da equação o máximo possível.
      Use a propriedade distributiva para remover qualquer parêntese.
      Combine termos semelhantes.
    2. Colete todos os termos variáveis em um lado da equação.
      Use a propriedade de adição ou subtração da igualdade.
    3. Colete todos os termos constantes do outro lado da equação.
      Use a propriedade de adição ou subtração da igualdade.
    4. Faça com que o coeficiente do termo variável seja igual a 1.
      Use a propriedade de multiplicação ou divisão da igualdade.
      Declare a solução para a equação.
    5. Verifique a solução. Substitua a solução na equação original para garantir que o resultado seja uma afirmação verdadeira.
    Exercício\(\PageIndex{4}\)

    Resolver:\(-(y + 9) = 8\)

    Resposta
      .
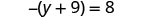
    Simplifique cada lado da equação o máximo possível distribuindo. .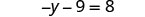
    O único termo y está no lado esquerdo, então todos os termos variáveis estão no lado esquerdo da equação.  
    Adicione 9 aos dois lados para obter todos os termos constantes no lado direito da equação. .
    Simplifique. .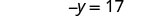
    Reescreva −y como −1y. .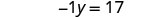
    Faça com que o coeficiente do termo variável seja igual a 1 dividindo os dois lados por −1. .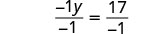
    Simplifique. .
    Confira: .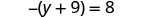  
    Seja y=−17. .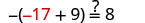  
      .  
      .  
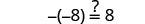
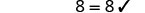
    Exercício\(\PageIndex{5}\)

    Resolver:\(-(y + 8) = -2\)

    Resposta

    \(y = -6\)

    Exercício\(\PageIndex{6}\)

    Resolver:\(-(z + 4) = -12\)

    Resposta

    \(z = 8\)

    Exercício\(\PageIndex{7}\)

    Resolver:\(5(a - 3) + 5 = -10\)

    Resposta
      .
    Simplifique cada lado da equação o máximo possível.  
    Distribuir. .
    Combine termos semelhantes. .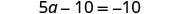
    O único termo está no lado esquerdo, então todos os termos variáveis estão em um lado da equação.  
    Adicione 10 aos dois lados para obter todos os termos constantes do outro lado da equação. .
    Simplifique. .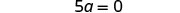
    Faça com que o coeficiente do termo variável seja igual a 11 dividindo os dois lados por 55. .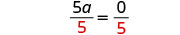
    Simplifique. .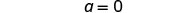
    Confira: .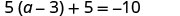  
    Seja a=0. .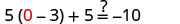  
      .  
      .  
      .  
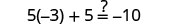
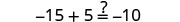
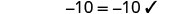
    Exercício\(\PageIndex{8}\)

    Resolver:\(2(m - 4) + 3 = -1\)

    Resposta

    \(m = 2\)

    Exercício\(\PageIndex{9}\)

    Resolver:\(7(n - 3) - 8 = -15\)

    Resposta

    \(n = 2\)

    Exercício\(\PageIndex{10}\)

    Resolver:\(\frac{2}{3}(6m - 3) = 8 - m\)

    Resposta
      .
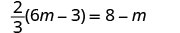
    Distribuir. .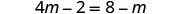
    Adicione m para obter as variáveis somente à esquerda. .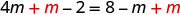
    Simplifique. .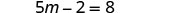
    Adicione 2 para obter constantes somente à direita. .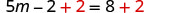
    Simplifique. .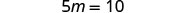
    Divida por 5. .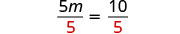
    Simplifique. .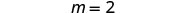
    Confira: .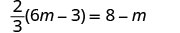  
    Deixe m=2. .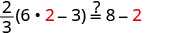  
      .  
      .  
      .  
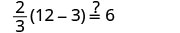
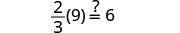
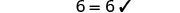
    Exercício\(\PageIndex{11}\)

    Resolver:\(\frac{1}{3}(6u + 3) = 7 - u\)

    Resposta

    \(u = 2\)

    Exercício\(\PageIndex{12}\)

    Resolver:\(\frac{2}{3}(9x - 12) = 8 + 2x\)

    Resposta

    \(x = 4\)

    Exercício\(\PageIndex{13}\)

    Resolver:\(8 - 2(3y + 5) = 0\)

    Resposta
      .
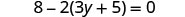
    Simplifique — use a propriedade distributiva. .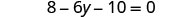
    Combine termos semelhantes. .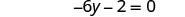
    Adicione 2 em ambos os lados para coletar constantes à direita. .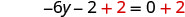
    Simplifique. .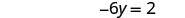
    Divida os dois lados por −6−6. .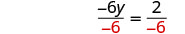
    Simplifique. .

    Verificação: Seja y=−13.

    .

    		  
    Exercício\(\PageIndex{14}\)

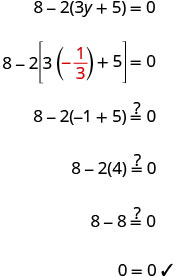
    Resolver:\(12 - 3(4j + 3) = -17\)

    Resposta

    \(j = \frac{5}{3}\)

    Exercício\(\PageIndex{15}\)

    Resolver:\(-6 - 8(k - 2) = -10\)

    Resposta

    \(k = \frac{5}{2}\)

    Exercício\(\PageIndex{16}\)

    Resolver:\(4(x - 1)-2=5(2x+3)+6\)

    Resposta
      .
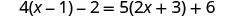
    Distribuir. .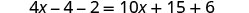
    Combine termos semelhantes. .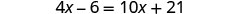
    Subtraia 4x para obter as variáveis apenas no lado direito desde então\(10>4\). .
    Simplifique. .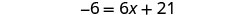
    Subtraia 21 para obter as constantes à esquerda. .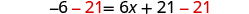
    Simplifique. .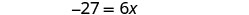
    Divida por 6. .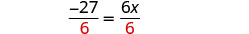
    Simplifique. .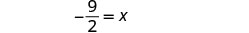
    Confira: .  
    Deixe\(x=-\frac{9}{2}\). .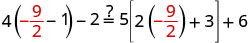  
      .  
      .  
      .  
      .  
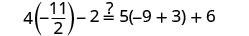
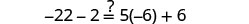
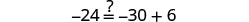
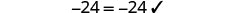
    Exercício\(\PageIndex{17}\)

    Resolver:\(6(p-3)-7=5(4p+3)-12\)

    Resposta

    \(p = -2\)

    Exercício\(\PageIndex{18}\)

    Resolver:\(8(q +1)-5=3(2q-4)-1\)

    Resposta

    \(q = -8\)

    Exercício\(\PageIndex{19}\)

    Resolver:\(10[3 - 8(2s-5)] = 15(40 - 5s)\)

    Resposta
      .
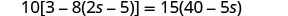
    Simplifique primeiro a partir dos parênteses mais internos. .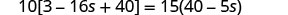
    Combine termos semelhantes entre colchetes. .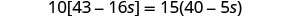
    Distribuir. .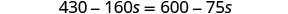
    Adicione 160s para obter os s para a direita. .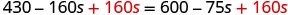
    Simplifique. .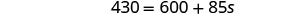
    Subtraia 600 para obter as constantes para a esquerda. .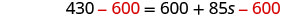
    Simplifique. .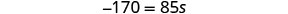
    Divida. .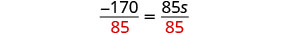
    Simplifique. .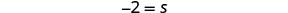
    Confira: .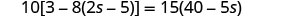  
    Substitua s=−2. .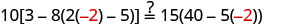  
      .  
      .  
      .  
      .  
      .  
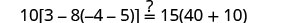
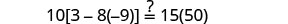
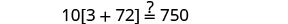
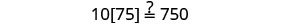
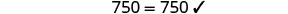
    Exercício\(\PageIndex{20}\)

    Resolver:\(6[4−2(7y−1)]=8(13−8y)\).

    Resposta

    \(y = -\frac{17}{5}\)

    Exercício\(\PageIndex{21}\)

    Resolver:\(12[1−5(4z−1)]=3(24+11z)\).

    Resposta

    \(z = 0\)

    Exercício\(\PageIndex{22}\)

    Resolver:\(0.36(100n+5)=0.6(30n+15)\).

    Resposta
      .
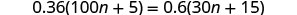
    Distribuir. .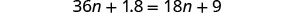
    Subtraia 18n para obter as variáveis à esquerda. .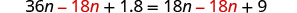
    Simplifique. .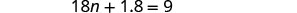
    Subtraia 1,8 para obter as constantes para a direita. .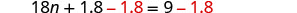
    Simplifique. .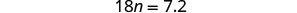
    Divida. .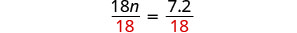
    Simplifique. .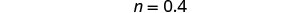
    Confira: .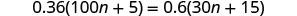  
    Seja n = 0,4. .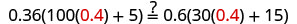  
      .  
      .  
      .  
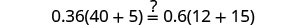
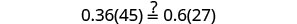
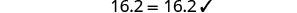
    Exercício\(\PageIndex{23}\)

    Resolver:\(0.55(100n+8)=0.6(85n+14)\).

    Resposta

    \(n = 1\)

    Exercício\(\PageIndex{24}\)

    Resolver:\(0.15(40m−120)=0.5(60m+12)\).

    Resposta

    \(m = -1\)

    Classificar equações

    Considere a equação que resolvemos no início da última seção, 7x+8=−13. A solução que encontramos foi x=−3. Isso significa que a equação 7x+8=−13 é verdadeira quando substituímos a variável, x, pelo valor −3. Mostramos isso quando verificamos a solução x=−3 e avaliamos 7x+8=−13 para x=−3.

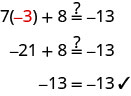
    Esta figura mostra por que podemos dizer que a equação 7x mais 8 é igual a menos 13 é verdadeira quando a variável x é substituída pelo valor negativo 3. A primeira linha mostra a equação com menos 3 substituído por x: 7 vezes menos 3 mais 8 pode ser igual a menos 13. Abaixo disso está a equação menos 21 mais 8 pode ser igual a menos 13. Abaixo está a equação menos 13 é igual a menos 13, com uma marca de verificação ao lado.

    Se calcularmos 7x+8 para um valor diferente de x, o lado esquerdo não será −13.

    A equação 7x+8=−13 é verdadeira quando substituímos a variável, x, pelo valor −3, mas não é verdadeira quando substituímos x por qualquer outro valor. Se a equação 7x+8=−13 é verdadeira ou não depende do valor da variável. Equações como essa são chamadas de equações condicionais.

    Todas as equações que resolvemos até agora são equações condicionais.

    EQUAÇÃO CONDICIONAL

    Uma equação verdadeira para um ou mais valores da variável e falsa para todos os outros valores da variável é uma equação condicional.

    Agora vamos considerar a equação 2y+6=2 (y+3). Você reconhece que o lado esquerdo e o lado direito são equivalentes? Vamos ver o que acontece quando resolvemos por y.

      .
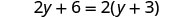    Distribuir. .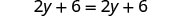
    Subtraia 2y para colocar os y's em um lado. .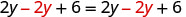
    Simplifique: os y's sumiram! .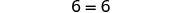

    Mas 6 = 6 é verdade.

    Isso significa que a equação 2y+6=2 (y+3) é verdadeira para qualquer valor de y. Dizemos que a solução para a equação são todos os números reais. Uma equação verdadeira para qualquer valor da variável como essa é chamada de identidade.

    IDENTIDADE

    Uma equação verdadeira para qualquer valor da variável é chamada de identidade.

    A solução de uma identidade são todos números reais.

    O que acontece quando resolvemos a equação 5z=5z−1?

      .
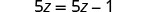    Subtraia 5z para obter a constante sozinha à direita. .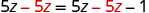
    Simplifique: os z's sumiram! .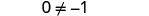

    Mas\(0\neq −1\).

    Resolver a equação 5z=5z−1 levou à falsa afirmação 0=−1. A equação 5z=5z−1 não será verdadeira para nenhum valor de z. Ela não tem solução. Uma equação que não tem solução, ou que é falsa para todos os valores da variável, é chamada de contradição.

    CONTRADIÇÃO

    Uma equação que é falsa para todos os valores da variável é chamada de contradição.

    Uma contradição não tem solução.

    Exercício\(\PageIndex{25}\)

    Classifique a equação como uma equação condicional, uma identidade ou uma contradição. Em seguida, indique a solução.

    \(6(2n−1)+3=2n−8+5(2n+1)\)


    Resposta
    .
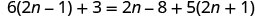
    Distribuir. .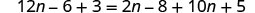
    Combine termos semelhantes. .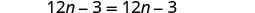
    Subtraia 12n para colocar os nn's em um lado. .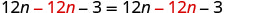
    Simplifique. .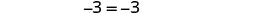
    Essa é uma afirmação verdadeira. A equação é uma identidade.
    A solução são todos números reais.
    Exercício\(\PageIndex{26}\)

    Classifique a equação como uma equação condicional, uma identidade ou uma contradição e, em seguida, declare a solução:

    \(4+9(3x−7)=−42x−13+23(3x−2)\)


    Resposta

    identidade; todos os números reais

    Exercício\(\PageIndex{27}\)

    Classifique a equação como uma equação condicional, uma identidade ou uma contradição e, em seguida, declare a solução:

    \(8(1−3x)+15(2x+7)=2(x+50)+4(x+3)+1\)


    Resposta

    identidade; todos os números reais

    Exercício\(\PageIndex{28}\)

    Classifique como uma equação condicional, uma identidade ou uma contradição. Em seguida, indique a solução.

    \(10+4(p−5)=0\)


    Resposta
      .
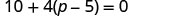
    Distribuir. .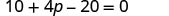
    Combine termos semelhantes. .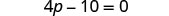
    Adicione 10 aos dois lados. .
    Simplifique. .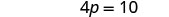
    Divida. .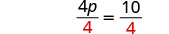
    Simplifique. .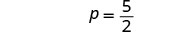
    A equação é verdadeira quando\(p = frac{5}{2}\). Essa é uma equação condicional.
    A solução é\(p = frac{5}{2}\).
    Exercício\(\PageIndex{29}\)

    Classifique a equação como uma equação condicional, uma identidade ou uma contradição e, em seguida, declare a solução:\(11(q+3)−5=19\)

    Resposta

    equação condicional;\ (q =\ frac {9} {11}\

    Exercício\(\PageIndex{30}\)

    Classifique a equação como uma equação condicional, uma identidade ou uma contradição e, em seguida, declare a solução:\(6+14(k−8)=95\)

    Resposta

    equação condicional;\(k = \frac{193}{14}\)

    Exercício\(\PageIndex{31}\)

    Classifique a equação como uma equação condicional, uma identidade ou uma contradição. Em seguida, indique a solução.

    \(5m+3(9+3m)=2(7m−11)\)


    Resposta
      .
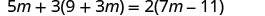
    Distribuir. .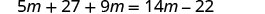
    Combine termos semelhantes. .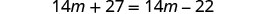
    Subtraia 14m de ambos os lados. .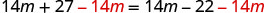
    Simplifique. .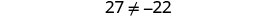
    Mas\(27\neq −22\). A equação é uma contradição.
    Não tem solução.
    Exercício\(\PageIndex{32}\)

    Classifique a equação como uma equação condicional, uma identidade ou uma contradição e, em seguida, declare a solução:

    \(12c+5(5+3c)=3(9c−4)\)


    Resposta

    contradição; sem solução

    Exercício\(\PageIndex{33}\)

    Classifique a equação como uma equação condicional, uma identidade ou uma contradição e, em seguida, declare a solução:

    \(4(7d+18)=13(3d−2)−11d\)


    Resposta

    contradição; sem solução

    Tipo de equação O que acontece quando você resolve isso? Solução
    Equação condicional Verdadeiro para um ou mais valores das variáveis e falso para todos os outros valores Um ou mais valores
    Identidade Verdadeiro para qualquer valor da variável Todos os números reais
    Contradição Falso para todos os valores da variável Sem solução

    Conceitos chave

    • Estratégia geral para resolver equações lineares
      1. Simplifique cada lado da equação o máximo possível.
        Use a propriedade distributiva para remover qualquer parêntese.
        Combine termos semelhantes.
      2. Colete todos os termos variáveis em um lado da equação.
        Use a propriedade de adição ou subtração da igualdade.
      3. Colete todos os termos constantes do outro lado da equação.
        Use a propriedade de adição ou subtração da igualdade.
      4. Faça com que o coeficiente do termo variável seja igual a 1.
        Use a propriedade de multiplicação ou divisão da igualdade.
        Declare a solução para a equação.
      5. Verifique a solução.
        Substitua a solução na equação original.