1.3: Use a linguagem da álgebra
- Page ID
- 184438
Ao final desta seção, você poderá:
- Use variáveis e símbolos algébricos
- Simplifique as expressões usando a ordem das operações
- Avalie uma expressão
- Identifique e combine termos semelhantes
- Traduzir uma frase em inglês para uma expressão algébrica
Use variáveis e símbolos algébricos
Suponha que este ano Greg tenha\(20\) anos e Alex tenha\(23\). Você sabe que Alex é\(3\) anos mais velho que Greg. Quando Greg estava\(12\), Alex estava\(15\). Quando Greg estiver\(35\), Alex será\(38\). Não importa a idade de Greg, a idade de Alex sempre será de 3 anos a mais, certo? Na linguagem da álgebra, dizemos que a idade de Greg e a idade de Alex são variáveis e a\(3\) é uma constante. As idades mudam (“variam”), mas os\(3\) anos entre elas sempre permanecem os mesmos (“constantes”). Como a idade de Greg e a idade de Alex sempre serão diferentes em\(3\) anos,\(3\) é a constante. Em álgebra, usamos letras do alfabeto para representar variáveis. Então, se chamarmos a idade de Greg\(g\), poderíamos usar\(g + 3g + 3\) para representar a idade de Alex. Veja a tabela\(\PageIndex{1}\).
| Idade de Greg | Idade de Alex |
|---|---|
| \(12\) | \(15\) |
| \(20\) | \(23\) |
| \(35\) | \(38\) |
| \(g\) | \(g+3\) |
As letras usadas para representar essas mudanças de idade são chamadas de variáveis. As letras mais usadas para variáveis são\(x, y, a, b,\)\(c\) e.
Uma variável é uma letra que representa um número cujo valor pode mudar.
Uma constante é um número cujo valor sempre permanece o mesmo.
Para escrever algebricamente, precisamos de alguns símbolos de operação, bem como números e variáveis. Existem vários tipos de símbolos que usaremos.
Há quatro operações aritméticas básicas: adição, subtração, multiplicação e divisão. Listaremos os símbolos usados para indicar essas operações abaixo (Tabela\(\PageIndex{2}\)). Você provavelmente reconhecerá alguns deles. \(\require{enclose}\)
| Operação | Notação | Diga: | O resultado é... |
|---|---|---|---|
| Adição | \(a+b\) | \(a\)mais\(b\) | a soma de\(a\) e\(b\) |
| Subtração | \(a−b\) | \(a\)menos\(b\) | a diferença de\(a\) e\(b\) |
| Multiplicação | \(a·b,ab,(a)(b),(a)b,a(b)\) | \(a\)vezes\(b\) | o produto de\(a\) e\(b\) |
| Divisão | \(a\div{b}, a/b,\dfrac{a}{b}, b \enclose{longdiv}{a}\) | \(a\)dividido por\(b\) | o quociente de\(a\) e\(b\),\(a\) é chamado de dividendo e\(b\) é chamado de divisor |
Realizamos essas operações em dois números. Ao traduzir da forma simbólica para o inglês, ou do inglês para a forma simbólica, preste atenção às palavras “de” e “e”.
- A diferença de\(9\) e\(2\) significa subtrair\(9\) e\(2\), em outras palavras,\(9\) menos\(2\), como escrevemos simbolicamente\(9−2\).
- O produto de\(4\) e\(8\) significa multiplicar\(4\) e\(8\), em outras palavras\(8\),\(4\) vezes, como escrevemos simbolicamente\(4\cdot 8\).
Em álgebra, o símbolo da cruz\(\times\),, não é usado para mostrar multiplicação porque esse símbolo pode causar confusão. \(3xy\)Significa\(3\times y\) ('três\(y\) vezes') ou\(3\cdot x \cdot y\) (três\(x\) vezes\(y\))? Para deixar claro, use\(\cdot\) ou parênteses para multiplicação.
Quando duas quantidades têm o mesmo valor, dizemos que são iguais e as conectamos com um sinal de igual.
\(a = b\)é lido “\(a\)é igual a\(b\)”
O símbolo\(“=”\) é chamado de sinal de igual.
Na reta numérica, os números aumentam à medida que vão da esquerda para a direita. A linha numérica pode ser usada para explicar os símbolos\(“<”\)\(“>"\) e.
\(a<b\)é lido “\(a\)é menor que\(b\)”
\(a\)está à\(b\) esquerda da linha numérica
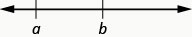
\(a>b\)é lido "\(a\)é maior que\(b\)”
\(a\)está à\(b\) direita da reta numérica
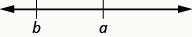
As expressões\(a < b\) ou\(a > b\) podem ser lidas da esquerda para a direita ou da direita para a esquerda, embora em inglês geralmente lemos da tabela da esquerda para a direita\(\PageIndex{3}\). Em geral,\(a < b\) é equivalente\(b > a\) a. Por exemplo,\(7 < 11\) é equivalente\(11 > 7\) a. E\(a > b\) é equivalente\(b < a\) a. Por exemplo,\(17 > 4\) é equivalente\(4 < 17\) a.
| Símbolos de desigualdade | Palavras |
|---|---|
| \(a \neq b\) | \(a\)não é igual a\(b\) |
| \(a < b\) | \(a\)é menor que\(b\) |
| \(a \leq b\) | \(a\)é menor ou igual a\(b\) |
| \(a > b\) | \(a\)é maior que\(b\) |
| \(a \geq b\) | \(a\)é maior ou não igual a\(b\) |
Traduzir da álgebra para o inglês:
- \(17 \leq 26\)
- \(8 \neq 17 - 3\)
- \(12 > 27 \div 3\)
- \(y + 7 < 19\)
- Responda
-
- \(17 \leq 26\),\(17\) é menor ou igual a\(26\)
- \(8 \neq 17 - 3\), não\(8\) é igual a\(17\) menos\(3\)
- \(12 > 27 \div 3\),\(12\) é maior do que\(27\) dividido por\(3\)
- \(y + 7 < 19\),\(y\) mais\(7\) é menor que\(19\)
Traduzir da álgebra para o inglês:
- \(14 \leq 27\)
- \(19 - 2 \neq 8\)
- \(12 > 4 \div 2\)
- \(x - 7 < 1\)
- Responda
-
- \(14\)é menor ou igual a\(27\)
- \(19\)menos não\(2\) é igual a\(8\)
- \(12\)é maior do que\(4\) dividido por\(2\)
- \(x\)menos\(7\) é menor que\(1\)
Traduzir da álgebra para o inglês:
- \(19 \leq 15\)
- \(7 = 12 - 5\)
- \(15 \div 3 < 8\)
- \(y + 3 < 6\)
- Responda
-
- \(19\)é maior ou igual a\(15\)
- \(7\)é igual a\(12\) menos\(5\)
- \(15\)dividido por\(3\) é menor que\(8\)
- \(y\)plus\(3\) é maior que\(6\)
Os símbolos de agrupamento em álgebra são muito parecidos com vírgulas, dois pontos e outros sinais de pontuação em inglês. Eles ajudam a esclarecer quais expressões devem ser mantidas juntas e separadas de outras expressões. Vamos apresentar três tipos agora.
\[\begin{align*} & \text{Parentheses} & & ( ) \\ & \text{Brackets} & & [ ] \\ & \text{Braces} & & \{ \} \end{align*}\]
Aqui estão alguns exemplos de expressões que incluem símbolos de agrupamento. Simplificaremos expressões como essas posteriormente nesta seção.
\[8(14−8) \qquad 21−3[2 + 4(9−8)] \qquad 24\div \{ 13−2[1(6−5)+4] \nonumber\}\]
Qual é a diferença em inglês entre uma frase e uma frase? Uma frase expressa um único pensamento que é incompleto por si só, mas uma frase faz uma declaração completa. “Correr muito rápido” é uma frase, mas “O jogador de futebol estava correndo muito rápido” é uma frase. Uma frase tem um sujeito e um verbo. Em álgebra, temos expressões e equações.
Uma expressão é um número, uma variável ou uma combinação de números e variáveis usando símbolos de operação.
Uma expressão é como uma frase em inglês. Aqui estão alguns exemplos de expressões:
| Expressão | Palavras | Frase em inglês |
|---|---|---|
| \(3 + 5\) | \(3\)mais\(5\) | a soma de três e cinco |
| \(n − 1\) | \(n\)menos um | a diferença de\(n\) e um |
| \(6\cdot 7\) | \(6\)vezes\(7\) | o produto de seis e sete |
| \(\dfrac{x}{y}\) | \(x\)dividido por\(y\) | o quociente de\(x\) e\(y\) |
Observe que as frases em inglês não formam uma frase completa porque a frase não tem um verbo. Uma equação são duas expressões vinculadas a um sinal de igual. Quando você lê as palavras que os símbolos representam em uma equação, você tem uma frase completa em inglês. O sinal de igual dá o verbo.
Uma equação são duas expressões conectadas por um sinal de igual.
Aqui estão alguns exemplos de equações.
| Equação | Frase em inglês |
|---|---|
| \(3+5=8\) | a soma de três e cinco é igual a oito |
| \(n−1=14\) | \(n\)menos um é igual a quatorze |
| \(6 \cdot 7=42\) | O produto de seis e sete é igual a quarenta e dois |
| \(x=53\) | \(x\)é igual a cinquenta e três |
| \(y+9=2y−3\) | \(y\)mais nove é igual a dois\(y\) menos três |
Determine se cada uma é uma expressão ou uma equação:
- \(2(x + 3) = 10\)
- \(4(y - 1) + 1\)
- \(x \div 25\)
- \(y + 8 = 40\)
- Responda
-
- \(2(x + 3) = 10\). Essa é uma equação — duas expressões estão conectadas com um sinal de igual.
- \(4(y - 1) + 1\). Isso é uma expressão — nenhum sinal igual.
- \(x \div 25\). Isso é uma expressão — nenhum sinal igual.
- \(y + 8 = 40\). Essa é uma equação — duas expressões estão conectadas com um sinal de igual.
Determine se cada uma é uma expressão ou uma equação:
- \(3(x - 7) = 27\)
- \(5(4y - 2) - 7\)
- Responda
-
- equação
- expressão
Determine se cada uma é uma expressão ou uma equação:
- \(y^{3} \div 14\)
- \(4x - 6 = 22\)
- Responda
-
- expressão
- equação
Suponha que precisemos multiplicar nove fatores de\(2\). Poderíamos escrever isso como\(2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\). Isso é entediante e pode ser difícil acompanhar todos esses 2s, então usamos expoentes. Nós escrevemos\(2\cdot 2 \cdot 2\) como\(2^{3}\) e\(2\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\) como\(2^{9}\). Em expressões como\(2^{3}\), o\(2\) é chamado de base e o\(3\) é chamado de expoente. O expoente nos diz quantas vezes precisamos multiplicar a base.

Lemos\(2^{3}\) como “dois elevado à terceira potência” ou “dois ao cubo”.
Dizemos que\(2^{3}\) está em notação exponencial e\(2\cdot 2 \cdot 2\) está em notação expandida.
\(a^{n}\)significa o produto de\(n\) fatores de\(a\).
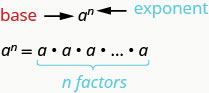
A expressão\(a^{n}\) é lida\(a\) ao\(n^{th}\) poder.
Embora leamos\(a^{n}\) como “\(a\)ao\(n^{th}\) poder”, geralmente lemos:
- \(a^{2}\)“um quadrado”
- \(a^{3}\)“um cubo”
Veremos mais tarde o porquê\(a^{2}\) e\(a^{3}\) teremos nomes especiais.
A tabela\(\PageIndex{6}\) mostra como lemos algumas expressões com expoentes.
| Expressão | Em palavras |
|---|---|
| \(7^{2}\) | \(7\)para a segunda potência ou\(7\) quadrado |
| \(5^{3}\) | \(5\)para a terceira potência ou ao\(5\) cubo |
| \(9^{4}\) | \(9\)para a quarta potência |
| \(12^{5}\) | \(12\)até a quinta potência |
Simplifique:\(3^{4}\)
- Responda
-
\[\quad 3^{4}\nonumber\]
\ [\ begin {align*} & Expanda a expressão & & & 3\ cdot 3\ cdot 3\\ [5pt]
&\ text {Multiplique da esquerda para a direita} & & & 9\ cdot 3\ cdot 3\\ [5pt]
&\ text {Multiply} & & & & & 27\ cdot 3\\ [5pt]
&\ text texto {Multiplicar} & & 81\ end {align*}\]
Simplifique:
- \(5^{3}\)
- \(1^{7}\)
- Responda
-
- \(125\)
- \(1\)
- \(7^{2}\)
- \(0^{5}\)
- Responda
-
- \(49\)
- \(0\)
Simplifique as expressões usando a ordem das operações
Simplificar uma expressão significa fazer todas as contas possíveis. Por exemplo, para simplificar, primeiro\(4\cdot 2 + 1\) multiplicamos\(4\cdot 2\) para obter\(8\) e depois adicionamos o\(1\) para obter\(9\). Um bom hábito a ser desenvolvido é trabalhar ao longo da página, escrevendo cada etapa do processo abaixo da etapa anterior. O exemplo que acabamos de descrever ficaria assim:
\[4\cdot 2 + 1\nonumber\]
\[8 + 1\nonumber\]
\[9\nonumber\]
Ao não usar um sinal de igual ao simplificar uma expressão, você pode evitar confundir expressões com equações.
Para simplificar uma expressão, faça todas as operações na expressão.
Introduzimos a maioria dos símbolos e notações usados na álgebra, mas agora precisamos esclarecer a ordem das operações. Caso contrário, as expressões podem ter significados diferentes e podem resultar em valores diferentes. Por exemplo, considere a expressão:
\[4 + 3\cdot 7\nonumber\]
Se você simplificar essa expressão, o que você obtém?
Alguns estudantes dizem:\(49\)
\[4 + 3\cdot 7\nonumber\]
Desde que\(4+3\) dá\(7\).
\[7 \cdot 7\nonumber\]
E\(7\cdot 7\) é\(49\)\[49\nonumber\]
Outros dizem:\(25\)
\[4 + 3\cdot 7\nonumber\]
Desde que\(3\cdot 7\) é\(21\).
\[4 + 21\nonumber\]
E\(21 + 4\) faz\(25\).
\[25\nonumber\]
Imagine a confusão em nosso sistema bancário se cada problema tivesse várias respostas corretas diferentes!
A mesma expressão deve dar o mesmo resultado. Então, os matemáticos estabeleceram desde o início algumas diretrizes que são chamadas de Ordem das Operações.
- Parênteses e outros símbolos de agrupamento
- Simplifique todas as expressões dentro dos parênteses ou outros símbolos de agrupamento, trabalhando primeiro nos parênteses mais internos.
- Expoentes
- Simplifique todas as expressões com expoentes.
- Multiplicação e divisão
- Execute todas as multiplicações e divisões em ordem da esquerda para a direita. Essas operações têm a mesma prioridade.
- Adição e subtração
- Execute todas as adições e subtrações na ordem da esquerda para a direita. Essas operações têm a mesma prioridade.
Fazer a atividade de Matemática Manipulativa “Jogo de 24” lhe dará prática usando a ordem das operações.
Os alunos costumam perguntar: “Como vou me lembrar do pedido?” Aqui está uma maneira de ajudá-lo a se lembrar: pegue a primeira letra de cada palavra-chave e substitua a frase boba: “Por favor, desculpe minha querida tia Sally”.
\ [\ begin {align*} &\ textbf {P}\ text {arentheses} & &\ textbf {P}\ text {lease}\\ [5pt]
&\ textbf {E}\ text {xponents} & &\ textbf {E}\ text {xcuse}\\ [5pt]
&\ textbf {M}\ texto {multiplicação}\ space\ textbf {D}\ texto {ivision} & &\ textbf {M}\ texto {y}\ espaço\ textbf {D}\ texto {ear}\\ [5pt]
&\ textbf {A}\ text {edição}\ space\ textbf {S}\ texto {subtração} & &\ textbf {A}\ texto {unt}\ space\ textbf {S}\ texto {aliado}\ end {align*}\]
É bom que “\(\textbf{M}\text{y}\space\textbf{D}\text{ear}\)” combine, pois isso nos lembra que minha multiplicação e minha divisão têm a mesma prioridade. Nem sempre fazemos multiplicação antes da divisão ou sempre fazemos divisão antes da multiplicação. Nós os fazemos em ordem da esquerda para a direita.
Da mesma forma, “\(\textbf{A}\text{unt}\space\textbf{S}\text{ally}\)” combina e nos lembra que uma adição e uma subtração também têm a mesma prioridade e as fazemos na ordem da esquerda para a direita.
Vamos tentar um exemplo.
Simplifique:
- \(4 + 3\cdot 7\)
- \((4 + 3)\cdot 7\)
- Responda
- 1.
\(4 + 3 \cdot 7\) Existem arênteses p? Não. Existem alguns expoentes? Não. Existe alguma multiplicação minha ou divisão de anúncios? Sim. Multiplique primeiro. \(4 + {\color{red}{3 \cdot 7}}\) Adicionar. \(4+21\) \(25\) 2.
\((4 + 3)\cdot 7\) Existem arênteses p? Sim. \({\color{red}{(4 + 3)}}\cdot 7\) Simplifique dentro dos parênteses. \(({\color{red}{7}})7\) Existem alguns expoentes? Não. Existe alguma multiplicação minha ou divisão de anúncios? Sim. Multiplique. \(49\)
Simplifique:
- \(12 - 5\cdot 2\)
- \((12 - 5)\cdot 2\)
- Responda
-
- \(2\)
- \(14\)
Simplifique:
- \(8 + 3\cdot 9\)
- \((8 + 3)\cdot 9\)
- Responda
-
- \(35\)
- \(99\)
Simplifique:\(18\div 6 + 4(5 - 2)\)
- Responda
-
Parênteses? Sim, subtraia primeiro. \(18\div 6 + 4(5 - 2)\)
\(18\div 6 + 4(3)\)Expoentes? Não. Multiplicação ou divisão? Sim. \({\color{red}{18\div 6}} + {\color{red}{4(3)}}\) Divida primeiro porque multiplicamos e dividimos da esquerda para a direita. \(3+{\color{red}{4(3)}}\) Alguma outra multiplicação ou divisão? Sim. Multiplique. \(3 + 12\) Alguma outra multiplicação ou divisão? Não. Alguma adição ou subtração? Sim. \(15\)
Simplifique:\(30\div 5 + 10(3 - 2)\)
- Responda
-
\(16\)
Simplifique:\(70\div 10 + 4(6 - 2)\)
- Responda
-
\(23\)
Quando há vários símbolos de agrupamento, simplificamos primeiro os parênteses mais internos e trabalhamos para fora.
Simplifique:\(5 + 2^{3} + 3[6 - 3(4 - 2)]\).
- Responda
-
\(5 + 2^{3} + 3[6 - 3(4 - 2)]\) Há algum parêntese (ou outro símbolo de agrupamento)? Sim. Concentre-se nos parênteses que estão dentro dos colchetes. \(5 + 2^{3} + 3[6 - 3{\color{red}{(4 - 2)}}]\) Subtrair. \(5 + 2^{3} + 3[6 - {\color{red}{3(2)}}]\) Continue dentro dos colchetes e multiplique. \(5 + 2^{3} + 3[{\color{red}{6 - 6}}]\) Continue dentro dos colchetes e subtraia. \(5 + 2^{3} + 3[{\color{red}{0}}]\) A expressão dentro dos colchetes não requer nenhuma simplificação adicional. Há algum expoente? Sim. \(5 + {\color{red}{2^{3}}}+ 3[0]\) Simplifique os expoentes \(5 + 8 + {\color{red}{3[0]}}\) Existe alguma multiplicação ou divisão? Sim. Multiplique. \({\color{red}{5 + 8}}+0\) Existe alguma adição ou subtração? Sim. Adicionar. \({\color{red}{13 + 0}}\) Adicionar. \(13\)
Simplifique:\(9 + 5^{3} - [4(9 + 3)]\).
- Responda
-
\(86\)
Simplifique:\(7^{2} - 2[4(5 + 1)]\).
- Responda
-
\(1\)
Avalie uma expressão
Nos últimos exemplos, simplificamos as expressões usando a ordem das operações. Agora vamos avaliar algumas expressões — novamente seguindo a ordem das operações. Avaliar uma expressão significa encontrar o valor da expressão quando a variável é substituída por um determinado número.
Avaliar uma expressão significa encontrar o valor da expressão quando a variável é substituída por um determinado número.
Para avaliar uma expressão, substitua esse número pela variável na expressão e, em seguida, simplifique a expressão.
Avalie\(7x - 4\), quando
- \(x = 5\)
- \(x = 1\)
- Responda
-
1.
quando\(x = {\color{red}{5}}\) \(7x - 4\) \(7({\color{red}{5}}) - 4\) Multiplique. \(35 - 4\) Subtrair. \(31\) 2.
quando\(x = {\color{red}{1}}\) \(7x - 4\) \(7({\color{red}{1}}) - 4\) Multiplique. \(7 - 4\) Subtrair. \(3\)
Avalie\(8x - 3\), quando
- \(x = 2\)
- \(x = 1\)
- Responda
-
- \(13\)
- \(5\)
Avalie\(4y - 4\), quando
- \(y = 3\)
- \(y = 5\)
- Responda
-
- \(8\)
- \(16\)
Avalie\(x = 4\), quando
- \(x^{2}\)
- \(3^{x}\)
- Responda
-
1.
\(x^{2}\) \(x\)Substitua por\({\color{red}{4}}\). \(({\color{red}{4}})^{2}\) Use a definição de expoente. \(4\cdot 4\) Simplifique. \(16\) 2.
\(3^{x}\) \(x\)Substitua por\({\color{red}{4}}\). \(3^ (click for details)\)Callstack: at (Idioma_Portugues/Livro:_Elementary_Algebra_(OpenStax)/01:_Fundações/1.03:_Use_a_linguagem_da_álgebra), /content/body/div[4]/div[5]/div/dl/dd/table[2]/tbody/tr[2]/td[2]/span/span, line 1, column 1Use a definição de expoente. \(3\cdot3\cdot3\cdot3\) Simplifique. \(81\)
Avalie\(x = 3\), quando
- \(x^{2}\)
- \(4^{x}\)
- Responda
-
- \(9\)
- \(64\)
Avalie\(x = 6\), quando
- \(x^{3}\)
- \(2^{x}\)
- Responda
-
- \(216\)
- \(64\)
Avalie\(2x^{2} + 3x + 8\) quando\(x = 4\).
- Responda
-
\(2x^{2} + 3x + 8\) Substituto\(x = {\color{red}{4}}\). \(\small{2x^{2} + 3x + 8}\)
\(2({\color{red}{4}})^{2} + 3({\color{red}{4}}) + 8\)Siga a ordem das operações. \(2(16)+3(4)+8\) \(32+12+8\) \(52\)
Avalie\(3x^{2} + 4x + 1\) quando\(x = 3\).
- Responda
-
\(40\)
Avalie\(6x^{2} - 4x - 7\) quando\(x = 2\).
- Responda
-
\(9\)
Identifique e combine termos semelhantes
As expressões algébricas são compostas por termos. Um termo é uma constante ou o produto de uma constante e uma ou mais variáveis.
Um termo é uma constante ou o produto de uma constante e uma ou mais variáveis.
Exemplos de termos são\(7, y, 5x^{2}, 9a\),\(b^{5}\) e.
A constante que multiplica a variável é chamada de coeficiente.
O coeficiente de um termo é a constante que multiplica a variável em um termo.
Pense no coeficiente como o número na frente da variável. O coeficiente do termo\(3x\) é\(3\). Quando escrevemos\(x\), o coeficiente é\(1\), desde\(x=1\cdot x\).
Identifique o coeficiente de cada termo:
- \(14y\)
- \(15x^{2}\)
- \(a\)
- Responda
-
- O coeficiente de\(14y\) é\(14\)
- O coeficiente de\(15x^{2}\) é\(15\)
- O coeficiente de\(a\) é\(1\) desde\(a=1a\).
Identifique o coeficiente de cada termo:
- \(17x\)
- \(41b^{2}\)
- \(z\)
- Responda
-
- \(14\)
- \(41\)
- \(1\)
Identifique o coeficiente de cada termo:
- \(9p\)
- \(13a^{2}\)
- \(y^{3}\)
- Responda
-
- \(9\)
- \(13\)
- \(1\)
Alguns termos compartilham traços comuns. Veja os 6 termos a seguir. Quais parecem ter características em comum?
\[5x \qquad 7 \qquad n^{2} \qquad 4 \qquad 3x \qquad 9n^{2}\nonumber\]
O\(7\) e o\(4\) são ambos termos constantes.
O\(5x\) e o\(3x\) são ambos termos com\(x\).
O\(n^{2}\) e o\(9n^{2}\) são ambos termos com\(n^{2}\).
Quando dois termos são constantes ou têm a mesma variável e expoente, dizemos que são como termos.
- \(7\)e\(4\) são como termos.
- \(5x\)e\(3x\) são como termos.
- \(x^{2}\)e\(9x^{2}\) são como termos.
Termos que são constantes ou têm as mesmas variáveis elevadas às mesmas potências são chamados de termos semelhantes.
Identifique termos semelhantes:\(y^{3},7x^{2}, 14, 23, 4y^{3}, 9x, 5x^{2}\).
- Responda
-
\(y^{3}\)e\(4y^{3}\) são como termos porque ambos têm\(y^{3}\); a variável e o expoente coincidem.
\(7x^{2}\)e\(5x^{2}\) são como termos porque ambos têm\(x^{2}\); a variável e o expoente coincidem.
\(14\)e\(23\) são como termos porque ambos são constantes.
Não há outro termo como\(9x\).
Identifique termos semelhantes:\(9, 2x^{3},y^{2}, 8x^{3}, 15, 9y, 11y^{2}\).
- Responda
-
\(9\)e\(15\),\(y^{2}\) e\(11y^{2}\),\(2x^{3}\) e\(8x^{3}\)
Identifique termos semelhantes:\(4x^{3},8x^{2}, 19, 3x^{3}, 24, 6x^{3}\).
- Responda
-
\(19\)e\(24\),\(8x^{2}\) e\(3x^{2}\),\(4x^{3}\) e\(6x^{3}\)
Identifique os termos em cada expressão.
- \(9x^{2}+7x+12\)
- \(8x+3y\)
- Responda
-
- Os termos de\(9x^{2}+7x+12\) são\(9x^{2}, 7x\),\(12\) e.
- Os termos de\(8x+3y\) são\(8x\)\(3y\) e.
Identifique os termos na expressão\(4x^{2}+5x+17\).
- Responda
-
\(4x^{2}, 5x, 17\)
Identifique os termos na expressão\(5x+2y\).
- Responda
-
\(5x, 2y\)
Se houver termos semelhantes em uma expressão, você pode simplificar a expressão combinando os termos semelhantes. O que você acha que\(4x+7x+x\) simplificaria? Se você pensasse\(12x\), você estaria certo!
\[\begin{array} { c } { 4 x + 7 x + x } \\ { x + x + x + x \quad + x + x + x + x + x + x + x \quad+ x } \\ { 12 x } \end{array}\]
Adicione os coeficientes e mantenha a mesma variável. Não importa o que seja x — se você tiver 4 de alguma coisa e adicionar mais 7 da mesma coisa e depois adicionar mais 1, o resultado será 12 delas. Por exemplo, 4 laranjas mais 7 laranjas mais 1 laranja são 12 laranjas. Discutiremos as propriedades matemáticas por trás disso mais tarde.
Simplifique:\(4x+7x+x\)
Adicione os coeficientes. \(12x\)
Simplifique:\(2x^{2} + 3x + 7 + x^{2} + 4x + 5\)
- Responda
-


Simplifique:\(3x^{2} + 7x + 9 + 7x^{2} + 9x + 8\).
- Responda
-
\(10x^{2}+16x+17\)
Simplifique:\(4y^{2} + 5y + 2 + 8y^{2} + 4y + 5\).
- Responda
-
\(12y^{2}+9y+7\)
- Identifique termos semelhantes.
- Reorganize a expressão de forma que os termos estejam juntos.
- Adicione ou subtraia os coeficientes e mantenha a mesma variável para cada grupo de termos semelhantes.
Traduzir uma frase em inglês para uma expressão algébrica
Na última seção, listamos muitos símbolos de operação usados em álgebra e, em seguida, traduzimos expressões e equações em frases e sentenças em inglês. Agora vamos reverter o processo. Vamos traduzir frases em inglês em expressões algébricas. Os símbolos e variáveis sobre os quais falamos nos ajudarão a fazer isso. A tabela os\(\PageIndex{7}\) resume.
| Operação | Frase | Expressão |
|---|---|---|
| Adição | \(a\)mais\(b\) a soma\(a\) e o\(b\) \(a\) aumento em\(b\) \(b\) mais do que\(a\) o total de\(a\) e\(b\) \(b\)adicionado a\(a\) |
\[a+b\] |
| Subtração | \(a\)menos\(b\) a diferença de\(a\) e\(b\) \(a\) diminuiu em\(b\) \(b\) menos do que\(a\) \(b\) subtraído de\(a\) |
\[a−b\] |
| Multiplicação | \(a\)vezes\(b\) o produto de\(a\) e\(b\) duas vezes\(a\) |
\[a\cdot b, ab, a(b), (a)(b)\] \[2a\] |
| Divisão | \(a\)dividido\(b\) pelo quociente de\(a\) e\(b\) pela razão de\(a\) e\(b\) \(b\) dividido em\(a\) |
\[a\div b, a/b, \frac{a}{b}, b \enclose{longdiv}{a}\] |
Examine atentamente essas frases usando as quatro operações:

Cada frase nos diz que devemos operar em dois números. Procure as palavras de e e para encontrar os números.
Traduza cada frase em inglês em uma expressão algébrica:
- a diferença de\(17x\) e\(5\)
- o quociente de\(10x^{2}\)\(7\) e.
- Responda
-
- A palavra-chave é diferença, o que nos diz que a operação é subtração. Procure as palavras de e e t para encontrar os números a serem subtraídos.
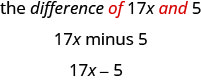
- A palavra-chave é “quociente”, o que nos diz que a operação é divisão.
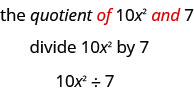
Isso também pode ser escrito\(10x^{2}/7\) ou\(\dfrac{10x^{2}}{7}\).
- A palavra-chave é diferença, o que nos diz que a operação é subtração. Procure as palavras de e e t para encontrar os números a serem subtraídos.
Traduza cada frase em inglês em uma expressão algébrica:
- a diferença de\(14x^{2}\) e\(13\)
- o quociente de\(12x\)\(2\) e.
- Responda
-
- \(14x^{2} - 13\)
- \(12x \div 2\)
Traduza cada frase em inglês em uma expressão algébrica:
- a soma de\(17y^{2}\) e\(19\)
- o produto de\(7\)\(y\) e.
- Responda
-
- \(17y^{2} + 19\)
- \(7y\)
Quantos anos você terá em oito anos? Que idade é oito anos a mais do que a sua agora? Você adicionou 8 à sua idade atual? Oito “mais que” significa 8 adicionados à sua idade atual. Quantos anos você tinha sete anos atrás? Isso é 7 anos a menos do que sua idade agora. Você subtrai 7 da sua idade atual. Sete “menos que” significa 7 subtraído da sua idade atual.
Traduza a frase em inglês em uma expressão algébrica:
- Dezessete a mais de\(y\)
- Nove a menos que\(9x^{2}\).
- Responda
-
- As palavras-chave são mais do que. Eles nos dizem que a operação é um acréscimo. Mais do que significa “adicionado a”.
\(\begin{array} { c } { \text { Seventeen more than } y } \\ { \text { Seventeen added to } y } \\ { y + 17 } \end{array}\)
- As palavras-chave são menores que. Eles nos dizem para subtrair. Menor que significa “subtraído de”.
\(\begin{array} { c } { \text { Nine less than } 9 x ^ { 2 } } \\ { \text { Nine subtracted from } 9 x ^ { 2 } } \\ { 9 x ^ { 2 } - 9 } \end{array}\)
- As palavras-chave são mais do que. Eles nos dizem que a operação é um acréscimo. Mais do que significa “adicionado a”.
Traduza a frase em inglês em uma expressão algébrica:
- Onze a mais de x
- Quatorze a menos que\(11a\).
- Responda
-
- \(x+11\)
- \(11a−14\)
Traduza a frase em inglês em uma expressão algébrica:
- \(13\)mais do que\(z\)
- \(18\)menos que\(8x\).
- Responda
-
1. \(z+13\)
2. \(8x−18\)
Traduza a frase em inglês em uma expressão algébrica:
- cinco vezes a soma de\(m\) e\(n\)
- a soma de cinco vezes\(m\)\(n\) e.
- Responda
-
Existem duas palavras de operação: o tempo nos diz para multiplicar e a soma nos diz para somar.
1. Como estamos multiplicando\(5\) vezes a soma, precisamos de parênteses ao redor da soma de\(m\) e\(n\),\((m+n)\). Isso nos força a determinar primeiro a soma. (Lembre-se da ordem das operações.)\[\begin{array} { c } { \text { five times the sum of } m \text { and } n } \\ { 5 ( m + n ) } \end{array}\]
2. Para fazer uma soma, procuramos as palavras “de” e “e” para ver o que está sendo adicionado. Aqui estamos tomando a soma de cinco vezes\(m\) e\ (n\.)\[\begin{array} { c } { \text { the sum of five times } m \text { and } n } \\ { 5 m + n } \end{array}\]
Traduza a frase em inglês em uma expressão algébrica:
- quatro vezes a soma de\(p\) e\(q\)
- a soma de quatro vezes\(p\)\(q\) e.
- Responda
-
- \(4(p+q)\)
- \(4p+q\)
Traduza a frase em inglês em uma expressão algébrica:
- a diferença de duas vezes x e\(8\),
- duas vezes a diferença de x\(8\) e.
- Responda
-
- \(2x−8\)
- \(2(x−8)\)
Posteriormente neste curso, aplicaremos nossas habilidades em álgebra para resolver aplicativos. O primeiro passo será traduzir uma frase em inglês para uma expressão algébrica. Veremos como fazer isso nos próximos dois exemplos.
O comprimento de um retângulo é\(6\) menor que a largura. Vamos\(w\) representar a largura do retângulo. Escreva uma expressão para o comprimento do retângulo.
- Responda
-
\[\begin{array} { l l } { \text { Write a phrase about the length of the rectangle. } } &{ 6 \text { less than the width } } \\ { \text { Substitute } w \text { for "the width." } } &{\text{6 less then w}} \\ { \text { Rewrite "less than" as "subtracted from." } } &{\text{6 subtracted from w}} \\ { \text { Translate the phrase into algebra. } } &{w - 6} \end{array}\]
O comprimento de um retângulo é\(7\) menor que a largura. Vamos\(w\) representar a largura do retângulo. Escreva uma expressão para o comprimento do retângulo.
- Responda
-
\(w - 7\)
A largura de um retângulo é\(6\) menor que o comprimento. Vamos\(l\) representar o comprimento do retângulo. Escreva uma expressão para a largura do retângulo.
- Responda
-
\(l - 6\)
June tem moedas de dez centavos e moedas na bolsa. O número de moedas de dez centavos é três vezes menor que o número de trimestres. Vamos\(q\) representar o número de trimestres. Escreva uma expressão para o número de moedas de dez centavos.
- Responda
-
\[\begin{array} { ll } { \text { Write the phrase about the number of dimes. } } &{\text{three less than four times the number of quarters}} \\ { \text { Substitute } q \text { for the number of quarters. } } &{\text{3 less than 4 times q}} \\ { \text { Translate "4 times } q \text { ." } } &{\text{3 less than 4q}} \\ { \text { Translate the phrase into algebra. } } &{\text{4q - 3}} \end{array}\]
Geoffrey tem moedas de dez centavos e moedas no bolso. O número de moedas de dez centavos é oito a menos que quatro vezes o número de trimestres. Vamos\(q\) representar o número de trimestres. Escreva uma expressão para o número de moedas de dez centavos.
- Responda
-
\(4q - 8\)
Lauren tem moedas de dez centavos e moedas na bolsa. O número de moedas de dez centavos é três a mais do que sete vezes o número de níqueis. Vamos\(n\) representar o número de níqueis. Escreva uma expressão para o número de moedas de dez centavos.
- Responda
-
\(7n + 3\)
Conceitos-chave
- Notação O resultado é...
\(\begin{array} { l l } {\bullet \space a + b } &{ \text { the sum of } a \text { and } b } \\ { \bullet \space a - b } &{ \text { the difference of } a \text { and } b } \\ {\bullet\space a \cdot b , a b , ( a ) ( b ) ( a ) b , a ( b ) } &{ \text { the product of } a \text { and } b } \\ {\bullet\space a \div b , a / b , \frac { a } { b } , b ) \overline{a} } &{ \text { the quotient of } a \text { and } b } \end{array}\) - Desigualdade
\(\begin{array} { l l } { \bullet \space a < b \text { is read "a is less than } b ^ { \prime \prime } } &{a \text { is to the left of } b \text { on the number line } } \\ { \bullet \space a > b \text { is read "a is greater than } b ^ { \prime \prime } } & { a \text { is to the right of } b \text { on the number line } } \end{array}\) - Palavras de símbolos de desigualdade
\(\begin{array} {ll} { \bullet a \neq b } &{ a \text { is not equal to } b } \\ { \bullet a < b } &{ a \text { is less than } b } \\ { \bullet a \leq b } &{ a \text { is less than or equal to } b } \\ { \bullet a > b } & { a \text { is greater than } b } \\ { \bullet a \geq b } & { a \text { is greater than or equal to } b } \end{array}\) - Símbolos de agrupamento
- Parênteses ()
- Colchetes []
- Chaves {}
- Notação exponencial
- \(a^{n}\)significa o produto de\(n\) fatores de\(a\). A expressão\(a^{n}\) é lida\(a\) ao\(n^{th}\) poder.
- Ordem das operações: Ao simplificar as expressões matemáticas, execute as operações na seguinte ordem:
- Parênteses e outros símbolos de agrupamento: simplifique todas as expressões dentro dos parênteses ou outros símbolos de agrupamento, trabalhando primeiro nos parênteses mais internos.
- Expoentes: simplifique todas as expressões com expoentes.
- Multiplicação e divisão: Execute todas as multiplicações e divisões em ordem da esquerda para a direita. Essas operações têm a mesma prioridade.
- Adição e subtração: Execute todas as adições e subtrações na ordem da esquerda para a direita. Essas operações têm a mesma prioridade.
- Combine termos semelhantes
- Identifique termos semelhantes.
- Reorganize a expressão de forma que os termos estejam juntos.
- Adicione ou subtraia os coeficientes e mantenha a mesma variável para cada grupo de termos semelhantes.
Glossário
- coeficiente
- O coeficiente de um termo é a constante que multiplica a variável em um termo.
- constante
- Uma constante é um número cujo valor sempre permanece o mesmo.
- símbolo de igualdade
- O símbolo “\(=\)” é chamado de sinal de igual. Lemos\(a=b\) como “\(a\)é igual a”\(b\).
- equação
- Uma equação são duas expressões conectadas por um sinal de igual.
- avaliar uma expressão
- Avaliar uma expressão significa encontrar o valor da expressão quando a variável é substituída por um determinado número.
- expressão
- Uma expressão é um número, uma variável ou uma combinação de números e variáveis usando símbolos de operação.
- termos semelhantes
- Termos que são constantes ou têm as mesmas variáveis elevadas às mesmas potências são chamados de termos semelhantes.
- simplificar uma expressão
- Para simplificar uma expressão, faça todas as operações na expressão.
- prazo
- Um termo é uma constante ou o produto de uma constante e de uma ou mais variáveis.
- variável
- Uma variável é uma letra que representa um número cujo valor pode mudar.


