17.4: Soluções em série de equações diferenciais
- Page ID
- 188135
- Use séries de potências para resolver equações diferenciais de primeira e segunda ordem.
Anteriormente, estudamos como as funções podem ser representadas como séries de potências,\(\displaystyle y(x)=\sum_{n=0}^{\infty} a_nx^n\). Também vimos que podemos encontrar representações em série das derivadas de tais funções diferenciando a série de potências termo por termo. Isso dá
\[y′(x)=\sum_{n=1}^{\infty}na_nx^{n−1} \nonumber \]
e
\[y″(x)=\sum_{n=2}^{\infty}n(n−1)a_nx^{n−2}. \nonumber \]
Em alguns casos, essas representações de séries de potência podem ser usadas para encontrar soluções para equações diferenciais.
Os exemplos e exercícios desta seção foram escolhidos para quais soluções de energia existem. No entanto, nem sempre existem soluções de energia. Aqueles que estão interessados em um tratamento mais rigoroso desse tópico devem revisar a seção de equações diferenciais do LibreTexts.
- Suponha que a equação diferencial tenha uma solução da forma\[y(x)=\sum_{n=0}^{\infty}a_nx^n. \nonumber \]
- Diferencie a série de potência termo por termo para obter\[y′(x)=\sum_{n=1}^{\infty}na_nx^{n−1} \nonumber \] e\[y″(x)=\sum_{n=2}^{\infty}n(n−1)a_nx^{n−2}. \nonumber \]
- Substitua as expressões da série de potências na equação diferencial.
- Reindexe as somas conforme necessário para combinar termos e simplificar a expressão.
- Equacione coeficientes de potências semelhantes de\(x\) para determinar valores para os coeficientes\(a_n\) na série de potências.
- Substitua os coeficientes novamente na série de potência e escreva a solução.
Encontre uma solução de série de potência para as seguintes equações diferenciais.
- \(y''−y=0\)
- \((x^2−1)y″+6xy′+4y=−4\)
Solução
Parte a
Suponha
\[y(x)=\sum_{n=0}^{∞}a_nx^n \tag{step 1} \]
Então,
\[y′(x)=\sum_{n=1}^{∞}na_nx^{n−1} \tag{step 2A} \]
e
\[y″(x)=\sum_{n=2}^{∞}n(n−1)a_nx^{n−2} \tag{step 2B} \]
Queremos encontrar valores para os coeficientes de\(a_n\) forma que
\[\begin{align*} &y″−y =0 \\[4pt] &\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}−\sum_{n=0}^{∞}a_nx^n =0 \tag{step 3}. \end{align*} \]
Queremos que os índices de nossas somas coincidam para que possamos expressá-los usando uma única soma. Ou seja, queremos reescrever a primeira soma para que ela comece com\(n=0\).
Para reindexar o primeiro termo,\(n\) substitua\(n+2\) por dentro da soma e altere o limite inferior de soma para\(n=0.\) Obtemos
\[\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}=\sum_{n=0}^∞ (n+2)(n+1)a_{n+2}x^n. \nonumber \]
Isso dá
\[\begin{align*}\sum_{n=0}^{∞}(n+2)(n+1)a_{n+2}x^n−\sum_{n=0}^{∞}a_nx_n &=0 \\[4pt] \sum_{n=0}^{∞}[(n+2)(n+1)a_{n+2}−a_n]x^n &=0 \tag{step 4}.\end{align*} \]
Como as expansões de funções em séries de potência são únicas, essa equação só pode ser verdadeira se os coeficientes de cada potência de\(x\) forem zero. Então nós temos
\[(n+2)(n+1)a_{n+2}−a_n=0 \text{ for }n=0,1,2,…. \nonumber \]
Essa relação de recorrência nos permite expressar cada coeficiente\(a_n\) em termos do coeficiente dois termos anteriores. Isso gera uma expressão para valores pares de\(n\) e outra expressão para valores ímpares de\(n\). Olhando primeiro para as equações que envolvem valores pares de\(n\), vemos que
\[\begin{align*}a_2 &= \dfrac{a_0}{2} \\[5pt] a_4 &= \dfrac{a_2}{4⋅3} = \dfrac{a_0}{4!}\\[5pt] a_6 &= \dfrac{a_4}{6⋅5} =\dfrac{a_0}{6!} \\ &\qquad ⋮ \end{align*}\]
Assim, em geral, quando\(n\) é par,
\[a_n=\dfrac{a_0}{n!}. \tag{step 5} \]
Para as equações que envolvem valores ímpares de,\(n,\) vemos que
\[\begin{align*}a_3 &=\dfrac{a_1}{3⋅2}=\dfrac{a_1}{3!} \\[5pt] a_5 &= \dfrac{a_3}{5⋅4}=\dfrac{a_1}{5!} \\[5pt] a_7 &= \dfrac{a_5}{7⋅6}=\dfrac{a_1}{7!} \\ &\qquad ⋮ \end{align*}\]
Portanto, em geral, quando\(n\) é estranho,
\[a_n=\dfrac{a_1}{n!}. \tag{step 5} \]
Juntando isso, temos
\[\begin{align*}y(x) &= \sum_{n=0}^{∞}a_nx^n \\[4pt] &=a_0+a_1x+\dfrac{a_0}{2}x^2+\dfrac{a_1}{3!}x^3+\dfrac{a_0}{4!}x^4+\dfrac{a_1}{5!}x^5+⋯. \end{align*}\]
Reindexando as somas para contabilizar os valores pares e ímpares de\(n\) separadamente, obtemos
\[y(x)=a_0 \sum_{k=0}^{∞} \dfrac{1}{(2k)!}x^{2k}+a_1 \sum_{k=0}^{∞}\dfrac{1}{(2k+1)!}x^{2k+1}. \tag{step 6} \]
Análise da parte a.
Como esperado para uma equação diferencial de segunda ordem, essa solução depende de duas constantes arbitrárias. No entanto, observe que nossa equação diferencial é uma equação diferencial de coeficiente constante, mas a solução da série de potências não parece ter a forma familiar (contendo funções exponenciais) que estamos acostumados a ver. Além disso, como\(y(x)=c_1e^x+c_2e^{−x}\) é a solução geral para essa equação, devemos ser capazes de escrever qualquer solução dessa forma, e não está claro se a solução da série de potência que acabamos de encontrar pode, de fato, ser escrita dessa forma.
Felizmente, depois de escrever as representações da série de potências de\(e^x\)\(e^{−x},\) e e fazer alguma álgebra, descobrimos que, se escolhermos
\[c_0=\dfrac{(a_0+a_1)}{2}, c_1=\dfrac{(a_0−a_1)}{2}, \nonumber \]
então temos\(a_0=c_0+c_1\) e\(a_1=c_0−c_1,\) e
\[\begin{align*}y(x) &= a_0+a_1x+\dfrac{a_0}{2}x^2+\dfrac{a_1}{3!}x^3+\dfrac{a_0}{4!}x^4+\dfrac{a_1}{5!}x^5+⋯ \\[4pt] &=(c_0+c_1)+(c_0−c_1)x+\dfrac{(c_0+c_1)}{2}x^2+\dfrac{(c_0−c_1)}{3!}x^3+\dfrac{(c_0+c_1)}{4!}x^4+\dfrac{(c_0−c_1)}{5!}x^5+⋯\\[4pt] &=c_0 \sum_{n=0}^{∞} \dfrac{x^n}{n!}+c_1 \sum_{n=0}^{∞}\dfrac{(−x)^n}{n!} \\[4pt] &=c_0e^x+c_1e^{−x}.\end{align*}\]
Então, de fato, encontramos a mesma solução geral. Observe que essa escolha de\(c_1\) e não\(c_2\) é óbvia. Esse é um caso em que sabemos qual deve ser a resposta e basicamente “fizemos engenharia reversa” em nossa escolha de coeficientes.
Parte b
Suponha
\[y(x)=\sum_{n=0}^{∞}a_nx^n \tag{step 1} \]
Então,
\[y′(x)=\sum_{n=1}^{∞}na_nx^{n−1} \tag{step 2} \]
e
\[y″(x)=\sum_{n=2}^{∞}n(n−1)a_nx^{n−2} \tag{step 2} \]
Queremos encontrar valores para os coeficientes de\(a_n\) forma que
\[\begin{align*}(x^2−1)y″+6xy′+4y &=−4 \\ (x^2−1) \sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+6x \sum_{n=1}^{∞}na_nx^{n−1}+4 \sum_{n=0}^{∞}a_nx^n &=−4 \\[4pt] x^2 \sum_{n=2}^{∞} n(n−1)a_nx^{n−2}−\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+6x \sum_{n=1}^{∞}na_nx^{n−1}+4 \sum_{n=0}^{∞}a_nx^n &=−4. \end{align*}\]
Tomando os fatores externos dentro das somações, obtemos
\[\sum_{n=2}^{∞}n(n−1)a_nx^n−\sum_{n=2}^{∞}n(n−1)a_nx^{n−2}+\sum_{n=1}^∞ 6na_nx^n+ \sum_{n=0}^∞ 4a_nx^n=−4 \tag{step 3}. \]
Agora, na primeira soma, vemos que quando\(n=0\) ou\(n=1\), o termo é avaliado como zero, então podemos adicionar esses termos de volta à nossa soma para obter
\[\sum_{n=2}^{∞}n(n−1)a_nx^n=\sum_{n=0}^∞ n(n−1)a_nx^n. \nonumber \]
Da mesma forma, no terceiro termo, vemos que quando\(n=0\), a expressão é avaliada como zero, então também podemos adicionar esse termo novamente. Nós temos
\[\sum_{n=1}^∞ 6na_nx^n=\sum_{n=0}^∞6na_nx^n. \nonumber \]
Então, precisamos apenas mudar os índices em nosso segundo mandato. Nós recebemos
\[\sum_{n=2}^∞n(n−1)a_nx^{n−2}=\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n. \nonumber \]
Assim, temos
\[\begin{align*} \sum_{n=0}^∞n(n−1)a_nx^n−\sum_{n=0}^∞(n+2)(n+1)a_{n+2}x^n+\sum_{n=0}^∞6na_nx^n+\sum_{n=0}^∞4a_nx^n &=−4 \tag{step 4} \\[4pt] \sum_{n=0}^∞[n(n−1)a_n−(n+2)(n+1)a_{n+2}+6na_n+4a_n]x^n &=−4 \\[4pt] \sum_{n=0}^∞[(n^2−n)a_n+6na_n+4a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞[n^2a_n+5na_n+4a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞ [(n^2+5n+4)a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \\[4pt] \sum_{n=0}^∞[(n+4)(n+1)a_n−(n+2)(n+1)a_{n+2}]x^n &=−4 \end{align*} \]
Observando os coeficientes de cada potência de\(x\), vemos que o termo constante deve ser igual a\(−4\), e os coeficientes de todas as outras potências de\(x\) devem ser zero. Então, olhando primeiro para o termo constante,
\[\begin{aligned}4a_0−2a_2 &=−4 \\ a_2 &=2a_0+2 \end{aligned} \tag{step 3} \]
\(n≥1\)Pois, nós temos
\[\begin{align*}(n+4)(n+1)a_n−(n+2)(n+1)a_{n+2} &= 0 \\[4pt] (n+1)[(n+4)a_n−(n+2)a_{n+2}] &=0. \end{align*}\]
Uma vez que\(n≥1, \; n+1≠0,\) vemos isso
\[(n+4)a_n−(n+2)a_{n+2}=0 \nonumber \]
e, portanto,
\[a_{n+2}=\dfrac{n+4}{n+2}a_n. \nonumber \]
Para valores pares de\(n\), temos
\[\begin{align*} a_4 &=\dfrac{6}{4}(2a_0+2)=3a_0+3 \\ a_6 &= \dfrac{8}{6}(3a_0+3)=4a_0+4 \\[4pt] &\qquad ⋮ \end{align*}\]
Em geral,
\[a_{2k}=(k+1)(a_0+1). \tag{step 5} \]
Para valores ímpares de\(n,\) nós temos
\[\begin{align*}a_3 &=\dfrac{5}{3}a_1 \\[4pt] a_5 &= \dfrac{7}{5}a_3=\dfrac{7}{3}a_1 \\[4pt] a_7 &=\dfrac{9}{7}a_5=\dfrac{9}{3} a_1=3a_1 \\[4pt] &\qquad ⋮ \end{align*}\]
Em geral,
\[a_{2k+1}=\dfrac{2k+3}{3}a_1. \tag{step 5 continued} \]
Juntando isso, temos
\[y(x)=\sum_{k=0}^∞ (k+1)(a_0+1)x^{2k}+\sum_{k=0}^∞ (\dfrac{2k+3}{3})a_1x^{2k+1}. \tag{step 6} \]
Encontre uma solução de série de potência para as seguintes equações diferenciais.
- \(y′+2xy=0\)
- \((x+1)y′=3y\)
- Dica
-
Siga a estratégia de resolução de problemas.
- Responda a
-
\(\displaystyle y(x)=a_0 \sum_{n=0}^∞ \dfrac{(−1)^n}{n!}x^{2n}=a_0e^{−x^2}\)
- Resposta b
-
\(y(x)=a_0(x+1)^3\)
Funções de Bessel
Encerramos esta seção com uma breve introdução às funções de Bessel. O tratamento completo das funções de Bessel está muito além do escopo deste curso, mas temos uma pequena amostra do tópico aqui para que possamos ver como soluções em série para equações diferenciais são usadas em aplicações do mundo real. A equação de ordem de Bessel\(n\) é dada por
\[x^2y″+xy′+(x^2−n^2)y=0. \nonumber \]
Essa equação surge em muitas aplicações físicas, particularmente aquelas que envolvem coordenadas cilíndricas, como a vibração de uma cabeça de tambor circular e o aquecimento ou resfriamento transitório de um cilindro. No próximo exemplo, encontramos uma solução de série de potência para a equação de Bessel de ordem 0.
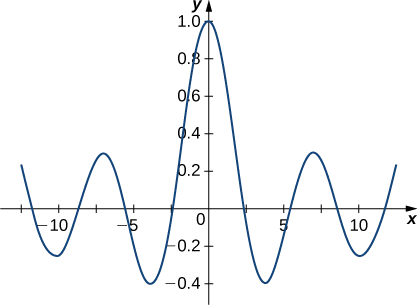
Encontre uma solução de série de potência para a equação de Bessel de ordem 0 e represente graficamente a solução.
Solução
A equação de Bessel de ordem 0 é dada por
\[x^2y″+xy′+x^2y=0. \nonumber \]
Nós assumimos uma solução do formulário\(\displaystyle y=\sum_{n=0}^∞ a_nx^n\). Então,\(\displaystyle y′(x)=\sum_{n=1}^∞ na_nx^{n−1}\) e\(\displaystyle y''(x)=\sum_{n=2}^∞n(n−1)a_nx^{n−2}.\) substituindo isso na equação diferencial, obtemos
\[\begin{align*} x^2 \sum_{n=2}^∞ n(n−1)a_nx^{n−2}+x \sum_{n=1}^∞ na_nx^{n−1}+x^2 \sum_{n=0}^∞ a_nx^n&=0 & & \text{Substitution.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+\sum_{n=1}^∞ na_nx^n+ \sum_{n=0}^∞ a_nx^{n+2}&=0 & & \text{Bring external factors within sums.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+\sum_{n=1}^∞ na_nx^n+\sum_{n=2}^∞ a_{n−2}x^n &=0 & & \text{Re-index third sum.} \\[5pt] \sum_{n=2}^∞ n(n−1)a_nx^n+a_1x+\sum_{n=2}^∞ na_nx^n+\sum_{n=2}^∞ a_{n−2}x^n &=0 & & \text{Separate }n=1 \text{ term from second sum.} \\[5pt] a_1x+\sum_{n=2}^∞ [n(n−1)a_n+na_n+a_{n−2}]x^n&=0 & & \text{Collect summation terms.} \\[5pt] a_1x+\sum_{n=2}^∞ [(n^2−n)a_n+na_n+a_{n−2}]x^n &=0 & & \text{Multiply through in first term.} \\[5pt] a_1x+\sum_{n=2}^∞ [n^2a_n+a_{n−2}]x^n &=0. & & \text{Simplify.} \end{align*}\]
Então\(a_1=0\), e para\(n≥2,\)
\[\begin{align*} n^2a_n+a_{n−2} &= 0 \\[4pt] a_n&=−\dfrac{1}{n^2}a_{n−2}. \end{align*} \nonumber \]
Porque\(a_1=0\), todos os termos ímpares são zero. Então, para valores iguais de\(n,\) nós temos
\[\begin{align*}a_2 &=−\dfrac{1}{2^2}a_0 \\[4pt] a_4 &= −\dfrac{1}{4^2}a_2=\dfrac{1}{4^2⋅2^2} a_0. \\[4pt] a_6 &=−\dfrac{1}{6^2}a_4 =−\dfrac{1}{6^2⋅4^2⋅2^2}a_0 \end{align*}\]
Em geral,
\[a_{2k}=\dfrac{(−1)^k}{(2)^{2k}(k!)^2}a_0. \nonumber \]
Assim, temos
\[y(x)=a_0 \sum_{k=0}^∞ \dfrac{(−1)^k}{(2)^{2k}(k!)^2}x^{2k}. \nonumber \]
O gráfico aparece abaixo.
Verifique se a expressão encontrada no Exemplo\(\PageIndex{2}\) é uma solução para a equação de Bessel de ordem 0.
- Dica
-
Diferencie a série de potências termo por termo e substitua-a pela equação diferencial.
Conceitos chave
- Às vezes, representações de funções em séries de potência podem ser usadas para encontrar soluções para equações diferenciais.
- Diferencie a série de potências termo por termo e substitua-a na equação diferencial para encontrar relações entre os coeficientes da série de potências.


