Skip to main content
Global

16.8E: Exercícios para a Seção 16.8

  1. Last updated
  2. Save as PDF
  • Page ID
    188483

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Para os exercícios 1 a 9, use um sistema algébrico computadorizado (CAS) e o teorema da divergência para avaliar a integral da superfície\(\displaystyle \int_S \vecs F \cdot \vecs n \, ds\) para a escolha dada\(\vecs F\) e a superfície limite.\(S.\) Para cada superfície fechada, suponha que\(\vecs N\) seja o vetor normal da unidade externa.

    1. [T]\(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\);\(S\) é a superfície do cubo\(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 < z \leq 1\).

    2. [T]\(\vecs F(x,y,z) = (\cos yz) \,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + 3z^2 \,\mathbf{\hat k}\);\(S\) é a superfície do hemisfério\(z = \sqrt{4 - x^2 - y^2}\) junto com o disco\(x^2 + y^2 \leq 4\) no\(xy\) plano.

    Resposta
    \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 75.3982\)

    3. [T]\(\vecs F(x,y,z) = (x^2 + y^2 - x^2)\,\mathbf{\hat i} + x^2 y\,\mathbf{\hat j} + 3z\,\mathbf{\hat k}; \)\(S\) é a superfície das cinco faces do cubo unitário\(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 < z \leq 1.\)

    4. [T]\(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}; \)\(S\) é a superfície do parabolóide\(z = x^2 + y^2\) para\(0 \leq z \leq 9\).

    Resposta
    \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 127.2345\)

    5. [T]\(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\);\(S\) é a superfície da esfera\(x^2 + y^2 + z^2 = 4\).

    6. [T]\(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + (z^2 - 1)\,\mathbf{\hat k}\);\(S\) é a superfície do sólido delimitada por cilindros\( x^2 + y^2 = 4\)\(z = 0\) e planos\(z = 1\) e.

    Resposta
    \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 37.699\)

    7. [T]\(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\);\(S\) é a superfície delimitada acima pela esfera\(\rho = 2\) e abaixo pelo cone\(\varphi = \dfrac{\pi}{4}\) em coordenadas esféricas. (Pense\(S\) como a superfície de uma “casquinha de sorvete”.)

    8. [T]\(\vecs F(x,y,z) = x^3\,\mathbf{\hat i} + y^3 \,\mathbf{\hat j} + 3a^2z \,\mathbf{\hat k} \, (constant \, a > 0)\);\(S\) é a superfície delimitada por cilindros\(x^2 + y^2 = a^2\)\(z = 0\) e planos\(z = 1\) e.

    Resposta
    \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = \dfrac{9\pi a^4}{2}\)

    9. [T] Integral de superfície\(\displaystyle \iint_S \vecs F \cdot dS\), onde\(S\) é o sólido delimitado pelo parabolóide\(z = x^2 + y^2\) e pelo plano\(z = 4\), e\(\vecs F(x,y,z) = (x + y^2z^2)\,\mathbf{\hat i} + (y + z^2x^2)\,\mathbf{\hat j} + (z + x^2y^2) \,\mathbf{\hat k}\)

    10. Use o teorema da divergência para calcular a integral da superfície\(\displaystyle \iint_S \vecs F \cdot dS\), onde\(\vecs F(x,y,z) = (e^{y^2} \,\mathbf{\hat i} + (y + \sin (z^2))\,\mathbf{\hat j} + (z - 1)\,\mathbf{\hat k}\) e\(S\) é o hemisfério superior\(x^2 + y^2 + z^2 = 1, \, z \geq 0\), orientado para cima.

    Resposta
    \(\displaystyle \iint_S \vecs F \cdot dS = \dfrac{\pi}{3}\)

    11. Use o teorema da divergência para calcular a integral da superfície\(\displaystyle \iint_S \vecs F \cdot dS\), onde\(\vecs F(x,y,z) = x^4\,\mathbf{\hat i} - x^3z^2\,\mathbf{\hat j} + 4xy^2z\,\mathbf{\hat k}\) e\(S\) é a superfície limitada por cilindros\(x^2 + y^2 = 1\)\(z = x + 2\) e planos\(z = 0\) e.

    12. Use o teorema da divergência para calcular a integral da superfície\(\displaystyle \iint_S \vecs F \cdot dS\), quando\(\vecs F(x,y,z) = x^2z^3 \,\mathbf{\hat i} + 2xyz^3\,\mathbf{\hat j} + xz^4 \,\mathbf{\hat k}\) e\(S\) é a superfície da caixa com vértices\((\pm 1, \, \pm 2, \, \pm 3)\).

    Resposta
    \(\displaystyle \iint_S \vecs F \cdot dS = 0\)

    13. Use o teorema da divergência para calcular a integral da superfície\(\displaystyle \iint_S \vecs F \cdot dS\), quando\(\vecs F(x,y,z) = z \, \tan^{-1} (y^2)\,\mathbf{\hat i} + z^3 \ln(x^2 + 1) \,\mathbf{\hat j} + z\,\mathbf{\hat k}\) e\(S\) faz parte do parabolóide\(x^2 + y^2 + z = 2\) que fica acima do plano\(z = 1\) e é orientado para cima.

    14. [T] Use um CAS e o teorema da divergência para calcular o fluxo\(\displaystyle \iint_S \vecs F \cdot dS\), onde\(\vecs F(x,y,z) = (x^3 + y^3)\,\mathbf{\hat i} + (y^3 + z^3)\,\mathbf{\hat j} + (z^3 + x^3)\,\mathbf{\hat k} \) e\(S\) é uma esfera com centro\((0, 0)\) e raio\(2.\)

    Resposta
    \(\displaystyle \iint_S \vecs F \cdot dS = 241.2743\)

    15. Use o teorema da divergência para calcular o valor da integral do fluxo\(\displaystyle \iint_S \vecs F \cdot dS\), onde\(\vecs F(x,y,z) = (y^3 + 3x)\,\mathbf{\hat i} + (xz + y)\,\mathbf{\hat j} + \left(z + x^4 \cos (x^2y)\right)\,\mathbf{\hat k}\) e\(S\) é a área da região delimitada por\(x^2 + y^2 = 1, \, x \geq 0, \, y \geq 0\),\(0 \leq z \leq 1\) e.

    0, y>0, and z>0. A quarter of a cylinder is drawn with center on the z axis. The arrows have positive x, y, and z components; they point away from the origin." data-type="media">Um campo vetorial em três dimensões, com foco na área com x 0, y>0 e z>0. Um quarto de um cilindro é desenhado com o centro no eixo z. As setas têm componentes positivos x, y e z; elas apontam para longe da origem." src="https://math.libretexts.org/@api/dek...16_08_202.jpeg">

    16. Use o teorema da divergência para calcular a integral do fluxo\(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = y\,\mathbf{\hat j} - z\,\mathbf{\hat k}\) and \(S\) consists of the union of paraboloid \(y = x^2 + z^2, \, 0 \leq y \leq 1\), and disk \(x^2 + z^2 \leq 1, \, y = 1\), oriented outward. What is the flux through just the paraboloid?

    Answer
    \(\displaystyle \iint_S \vecs F \cdot dS = -\pi\)

    17. Use the divergence theorem to compute flux integral \(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z^4 \,\mathbf{\hat k}\) and \(S\) is a part of cone \(z = \sqrt{x^2 + y^2}\) beneath top plane \(z = 1\) oriented downward.

    18. Use the divergence theorem to calculate surface integral \(\displaystyle \iint_S \vecs F \cdot dS\) for \(\vecs F(x,y,z) = x^4\,\mathbf{\hat i} - x^3z^2\,\mathbf{\hat j} + 4xy^2 z\,\mathbf{\hat k}\), where \(S\) is the surface bounded by cylinder \(x^2 + y^2 = 1\) and planes \(z = x + 2\) and \(z = 0\).

    Answer
    \(\displaystyle \iint_S \vecs F \cdot dS = \dfrac{2\pi}{3}\)

    19. Consider \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + xy\,\mathbf{\hat j} + (z + 1)\,\mathbf{\hat k}\). Let \(E\) be the solid enclosed by paraboloid \(z = 4 - x^2 - y^2\) and plane \(z = 0\) with normal vectors pointing outside \(E.\) Compute flux \(\vecs F\) across the boundary of \(E\) using the divergence theorem.

    In exercises 20 - 23, use a CAS along with the divergence theorem to compute the net outward flux for the fields across the given surfaces \(S.\)

    20. [T] \(\vecs F = \langle x,\, -2y, \, 3z \rangle; \) \(S\) is sphere \(\{(x,y,z) : x^2 + y^2 + z^2 = 6 \}\).

    Answer
    \(15\sqrt{6}\pi\)

    21. [T] \(\vecs F = \langle x, \, 2y, \, z \rangle\); \(S\) is the boundary of the tetrahedron in the first octant formed by plane \(x + y + z = 1\).

    22. [T] \(\vecs F = \langle y - 2x, \, x^3 - y, \, y^2 - z \rangle\); \(S\) is sphere \(\{(x,y,z) \,:\, x^2 + y^2 + z^2 = 4\}.\)

    Answer
    \(-\dfrac{128}{3} \pi\)

    23. [T] \(\vecs F = \langle x,y,z \rangle\); \(S\) is the surface of paraboloid \(z = 4 - x^2 - y^2\), for \(z \geq 0\), plus its base in the \(xy\)-plane.

    For exercises 24 - 26, use a CAS and the divergence theorem to compute the net outward flux for the vector fields across the boundary of the given regions \(D.\)

    24. [T] \(\vecs F = \langle z - x, \, x - y, \, 2y - z \rangle\); \(D\) is the region between spheres of radius 2 and 4 centered at the origin.

    Answer
    \(-703.7168\)

    25. [T] \(\vecs F = \dfrac{\vecs r}{\|\vecs r\|} = \dfrac{\langle x,y,z\rangle}{\sqrt{x^2+y^2+z^2}}\); \(D\) is the region between spheres of radius 1 and 2 centered at the origin.

    26. [T] \(\vecs F = \langle x^2, \, -y^2, \, z^2 \rangle\); \(D\) is the region in the first octant between planes \(z = 4 - x - y\) and \(z = 2 - x - y\).

    Answer
    \(20\)

    27. Let \(\vecs F(x,y,z) = 2x\,\mathbf{\hat i} - 3xy\,\mathbf{\hat j} + xz^2\,\mathbf{\hat k}\). Use the divergence theorem to calculate \(\displaystyle \iint_S \vecs F \cdot dS\), where \(S\) is the surface of the cube with corners at \((0,0,0), \, (1,0,0), \, (0,1,0), \, (1,1,0), \, (0,0,1), \, (1,0,1), \, (0,1,1)\), and \((1,1,1)\), oriented outward.

    28. Use the divergence theorem to find the outward flux of field \(\vecs F(x,y,z) = (x^3 - 3y)\,\mathbf{\hat i} + (2yz + 1)\,\mathbf{\hat j} + xyz\,\mathbf{\hat k}\) through the cube bounded by planes \(x = \pm 1, \, y = \pm 1, \) and \(z = \pm 1\).

    Answer
    \(\displaystyle \iint_S \vecs F \cdot dS = 8\)

    29. Let \(\vecs F(x,y,z) = 2x\,\mathbf{\hat i} - 3y\,\mathbf{\hat j} + 5z\,\mathbf{\hat k}\) and let \(S\) be hemisphere \(z = \sqrt{9 - x^2 - y^2}\) together with disk \(x^2 + y^2 \leq 9\) in the \(xy\)-plane. Use the divergence theorem.

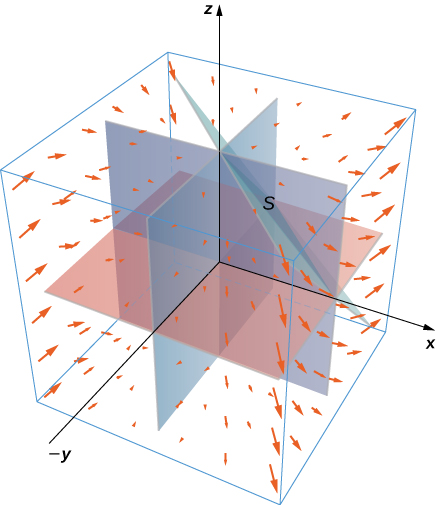
    30. Evaluate \(\displaystyle \iint_S \vecs F \cdot \vecs n \, dS\), where \(\vecs F(x,y,z) = x^2 \,\mathbf{\hat i} + xy\,\mathbf{\hat j} + x^3y^3\,\mathbf{\hat k}\) and \(S\) is the surface consisting of all faces except the tetrahedron bounded by plane \(x + y + z = 1\) and the coordinate planes, with outward unit normal vector \(\vecs N.\)

    A vector field in three dimensions, with arrows becoming larger the further away from the origin they are, especially in their x components. S is the surface consisting of all faces except the tetrahedron bounded by the plane x + y + z = 1. As such, a portion of the given plane, the (x, y) plane, the (x, z) plane, and the (y, z) plane are shown. The arrows point towards the origin for negative x components, away from the origin for positive x components, down for positive x and negative y components, as well as positive y and negative x components, and for positive x and y components, as well as negative x and negative y components.

    Resposta
    \(\displaystyle \iint_S \vecs F \cdot \vecs n \, dS = \dfrac{1}{8}\)

    31. Encontre o fluxo de campo externo líquido\(\vecs F = \langle bz - cy, \, cx - az, \, ay - bx \rangle\) em qualquer superfície lisa e fechada em\(R^3\) onde\(a, \, b,\) e\(c\) seja constante.

    32. Use o teorema da divergência para avaliar\(\displaystyle \iint_S ||\vecs R||\vecs R \cdot \vecs n \, ds,\) onde\(\vecs R(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\) e\(S\) é esfera\(x^2 + y^2 + z^2 = a^2\), com constante\(a > 0\).

    Resposta
    \(\displaystyle \iint_S ||\vecs R||\vecs R \cdot \vecs n \, ds = 4\pi a^4\)

    33. Use o teorema da divergência para avaliar\(\displaystyle \iint_S \vecs F \cdot dS,\) onde\(\vecs F(x,y,z) = y^2 z\,\mathbf{\hat i} + y^3\,\mathbf{\hat j} + xz\,\mathbf{\hat k}\) e\(S\) é o limite do cubo definido por\(-1 \leq x \leq 1, \, -1 \leq y \leq 1\),\(0 \leq z \leq 2\) e.

    34. \(R\)Seja a região definida por\(x^2 + y^2 + z^2 \leq 1\). Use o teorema da divergência para encontrar\(\displaystyle \iiint_R z^2 \, dV.\)

    Resposta
    \(\displaystyle \iiint_R z^2 dV = \dfrac{4\pi}{15}\)

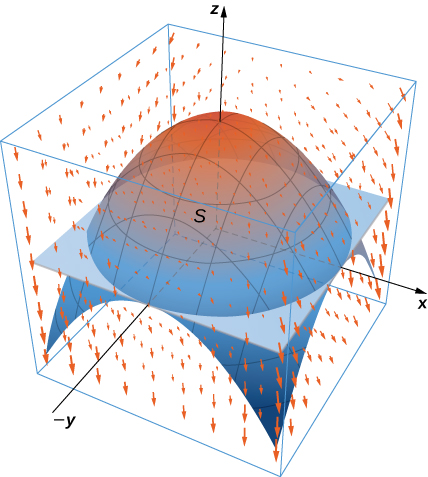
    35. \(E\)Seja o sólido delimitado pelo\(xy\) plano -e pelo parabolóide\(z = 4 - x^2 - y^2\), de forma que\(S\) seja a superfície da peça parabolóide junto com o disco no\(xy\) plano -que forma sua parte inferior. Se\(\vecs F(x,y,z) = (xz \, \sin(yz) + x^3) \,\mathbf{\hat i} + \cos (yz) \,\mathbf{\hat j} + (3zy^2 - e^{x^2+y^2})\,\mathbf{\hat k}\), encontre\(\displaystyle \iint_S \vecs F \cdot dS\) usando o teorema da divergência.

    Um campo vetorial em três dimensões com todas as setas apontando para baixo. Eles parecem seguir o caminho do parabolóide traçado, abrindo-se para baixo com o vértice na origem. S é a superfície desse parabolóide e o disco no plano (x, y) que forma sua parte inferior.

    36. Deixe

    Template:ContribOpenStaxCalc