15.7E: Exercícios para a Seção 15.7

Last updated
Save as PDF

Page ID: 188114

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 6, a função$T : S \rightarrow R, \space T (u,v) = (x,y)$ na região$S = \big\{(u,v) \,|\, 0 \leq u \leq 1, \space 0 \leq v \leq 1\big\}$ delimitada pela unidade quadrada é dada, onde$R \in R^2$ está a imagem de$S$ abaixo$T$.

a. Justifique que a função$T$ é uma$C^1$ transformação.

b. Encontre as imagens dos vértices da unidade quadrada$S$ por meio da função$T$.

c. Determine a imagem$R$ da unidade quadrada$S$ e represente-a graficamente.

1. $x = 2u, \space y = 3v$

2. $x = \frac{u}{2}, \space y = \frac{v}{3}$

Resposta

a.$T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = \frac{u}{2}$$y = h(u,v) = \frac{v}{3}$ e. As funções$g$$h$ são contínuas e diferenciáveis, e as derivadas parciais$g_u (u,v) = \frac{1}{2}, \space g_v (u,v) = 0, \space h_u (u,v) = 0$ e$h_v (u,v) = \frac{1}{3}$ são contínuas$S$;

b.$T(0,0) = (0,0), \space T(1,0) = \left(\frac{1}{2},0\right), \space T(0,1) = \left(0,\frac{1}{3}\right)$, e$T(1,1) = \left(\frac{1}{2}, \frac{1}{3} \right)$;

c.$R$ é o retângulo de vértices$(0,0), \space \left(0,\frac{1}{3}\right), \space \left(\frac{1}{2}, \frac{1}{3} \right)$ e$\left(0,\frac{1}{3}\right)$ no$xy$ plano -; a figura a seguir.

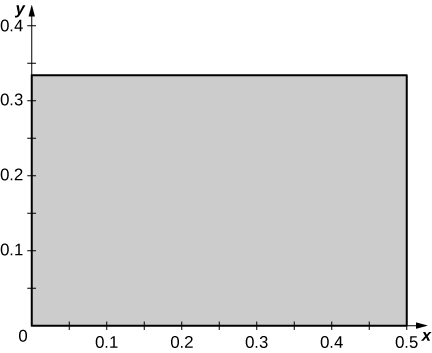
$Um retângulo com um canto na origem, comprimento horizontal 0,5 e altura vertical 0,34.$

3. $x = u - v, \space y = u + v$

4. $x = 2u - v, \space y = u + 2v$

Answer

a. $T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = 2u - v$ and $y = h(u,v) = u + 2v$. The functions $g$ and $h$ are continuous and differentiable, and the partial derivatives $g_u (u,v) = 2, \space g_v (u,v) = -1, \space h_u (u,v) = 1$ and $h_v (u,v) = 2$ are continuous on $S$;

b. $T(0,0) = (0,0), \space T(1,0) = (2,1), \space T(0,1) = (-1,2)$, and $T(1,1) = (1,3)$;

c. $R$ is the parallelogram of vertices $(0,0), \space (2,1) \space (1,3)$, and $(-1,2)$ in the $xy$-plane; the following figure.

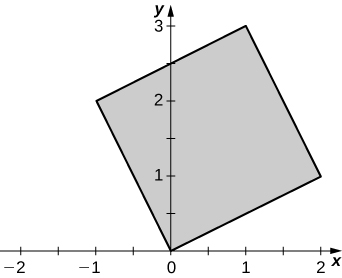
$A square of side length square root of 5 with one corner at the origin and another at (2, 1).$

5. $x = u^2, \space y = v^2$

6. $x = u^3, \space y = v^3$

Resposta

a.$T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = u^3$$y = h(u,v) = v^3$ e. As funções$g$$h$ são contínuas e diferenciáveis, e as derivadas parciais$g_u (u,v) = 3u^2, \space g_v (u,v) = 0, \space h_u (u,v) = 0$ e$h_v (u,v) = 3v^2$ são contínuas$S$;

b.$T(0,0) = (0,0), \space T(1,0) = (1,0), \space T(0,1) = (0,1)$, e$T(1,1) = (1,1)$;

c.$R$ é a unidade quadrada no$xy$ plano -veja a figura na resposta ao exercício anterior.

Nos exercícios 7 a 12, determine se as transformações$T : S \rightarrow R$ são individuais ou não.

7. $x = u^2, \space y = v^2$, onde$S$ está o retângulo de vértices$(-1,0), \space (1,0), \space (1,1)$,$(-1,1)$ e.

8. $x = u^4, \space y = u^2 + v$, onde$S$ está o triângulo de vértices$(-2,0), \space (2,0)$,$(0,2)$ e.

Resposta: $T$não é um para um: dois pontos$S$ têm a mesma imagem. De fato,$T(-2,0) = T(2,0) = (16,4)$.

9. $x = 2u, \space y = 3v$, onde$S$ é o quadrado dos vértices$(-1,1), \space (-1,-1), \space (1,-1)$,$(1,1)$ e.

10. $T(u, v) = (2u - v, u),$onde$S$ está o triângulo com vértices$(-1,1), \, (-1,-1)$,$(1,-1)$ e.

Resposta: $T$é individual: argumentamos por contradição. $T(u_1,v_1) = T(u_2,v_2)$implica$2u_1 - v_1 = 2u_2 - v_2$$u_1 = u_2$ e. Assim,$u_1 = u+2$$v_1 = v_2$ e.

11. $x = u + v + w, \space y = u + v, \space z = w$, onde$S = R = R^3$.

12. $x = u^2 + v + w, \space y = u^2 + v, \space z = w$, onde$S = R = R^3$.

Resposta: $T$não é um para um:$T(1,v,w) = (-1,v,w)$

Nos exercícios 13 a 18, as transformações$T : R \rightarrow S$ são individuais. Encontre suas transformações inversas relacionadas$T^{-1} : R \rightarrow S$.

13. $x = 4u, \space y = 5v$, onde$S = R = R^2$.

14. $x = u + 2v, \space y = -u + v$, onde$S = R = R^2$.

Resposta: $u = \frac{x-2y}{3}, \space v= \frac{x+y}{3}$

15. $x = e^{2u+v}, \space y = e^{u-v}$, onde$S = R^2$ e$R = \big\{(x,y) \,|\, x > 0, \space y > 0\big\}$

16. $x = \ln u, \space y = \ln(uv)$, onde$S = \big\{(u,v) \,|\, u > 0, \space v > 0\big\}$$R = R^2$ e.

Resposta: $u = e^x, \space v = e^{-x+y}$

17. $x = u + v + w, \space y = 3v, \space z = 2w$, onde$S = R = R^3$.

18. $x = u + v, \space y = v + w, \space z = u + w$, onde$S = R = R^3$.

Resposta: $u = \frac{x-y+z}{2}, \space v = \frac{x+y-z}{2}, \space w = \frac{-x+y+z}{2}$

Nos exercícios 19 a 22, a transformação$T : S \rightarrow R, \space T (u,v) = (x,y)$ e a região$R \subset R^2$ são dadas. Encontre a região$S \subset R^2$.

19. $x = au, \space y = bv, \space R = \big\{(x,y) \,|\, x^2 + y^2 \leq a^2 b^2\big\}$onde$a,b > 0$

20. $x = au, \space y = bc, \space R = \big\{(x,y) \,|\, \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1\big\}$, onde$a,b > 0$

Resposta: $S = \big\{(u,v) \,|\, u^2 + v^2 \leq 1\big\}$

21. $x = \frac{u}{a}, \space y = \frac{v}{b}, \space z = \frac{w}{c}, \space R = \big\{(x,y)\,|\,x^2 + y^2 + z^2 \leq 1\big\}$, onde$a,b,c > 0$

22. $x = au, \space y = bv, \space z = cw, \space R = \big\{(x,y)\,|\,\frac{x^2}{a^2} - \frac{y^2}{b^2} - \frac{z^2}{c^2} \leq 1, \space z > 0\big\}$, onde$a,b,c > 0$

Resposta: $R = \big\{(u,v,w)\,|\,u^2 - v^2 - w^2 \leq 1, \space w > 0\big\}$

Nos exercícios 23 a 32, encontre o Jacobiano$J$ da transformação.

23. $x = u + 2v, \space y = -u + v$

24. $x = \frac{u^3}{2}, \space y = \frac{v}{u^2}$

Resposta: $\frac{3}{2}$

25. $x = e^{2u-v}, \space y = e^{u+v}$

26. $x = ue^v, \space y = e^{-v}$

Resposta: $-1$

27. $x = u \space \cos (e^v), \space y = u \space \sin(e^v)$

28. $x = v \space \sin (u^2), \space y = v \space \cos(u^2)$

Resposta: $2uv$

29. $x = u \space \cosh v, \space y = u \space \sinh v, \space z = w$

30. $x = v \space \cosh \left(\frac{1}{u}\right), \space y = v \space \sinh \left(\frac{1}{u}\right), \space z = u + w^2$

Resposta: $\frac{v}{u^2}$

31. $x = u + v, \space y = v + w, \space z = u$

32. $x = u - v, \space y = u + v, \space z = u + v + w$

Resposta: $2$

33. A região triangular$R$ com os vértices$(0,0), \space (1,1)$, e$(1,2)$ é mostrada na figura a seguir.

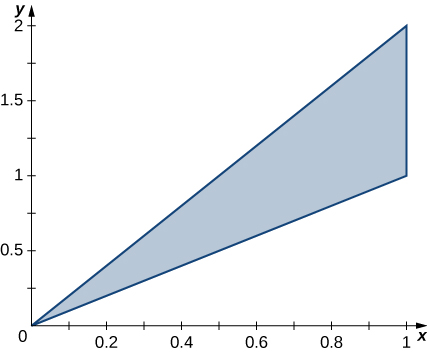
$Um triângulo com cantos na origem, (1, 1) e (1, 2).$

a. Encontre uma transformação$T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv)$, where $a,b,c$, and $d$ are real numbers with $ad - bc \neq 0$ such that $T^{-1} (0,0) = (0,0), \space T^{-1} (1,1) = (1,0)$, and $T^{-1}(1,2) = (0,1)$.

b. Use the transformation $T$ to find the area $A(R)$ of the region $R$.

34. The triangular region $R$ with the vertices $(0,0), \space (2,0)$, and $(1,3)$ is shown in the following figure.

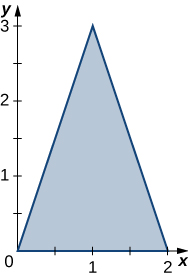
$A triangle with corners at the origin, (2, 0), and (1, 3).$

a. Encontre uma transformação$T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv)$$a,b,c$, onde e$d$ são números reais com$ad - bc \neq 0$ tal que$T^{-1} (0,0) = (0,0), \space T^{-1} (2,0) = (1,0)$,$T^{-1}(1,3) = (0,1)$ e.

b. Use a transformação$T$ para encontrar a área$A(R)$ da região$R$.

Resposta: a.$T (u,v) = (2u + v, \space 3v)$
b. A área de$R$ é$\displaystyle A(R) = \int_0^3 \int_{y/3}^{(6-y)/3} \, dx \, dy = \int_0^1 \int_0^{1-u} \left|\frac{\partial (x,y)}{\partial (u,v)}\right| \, dv \space du = \int_0^1 \int_0^{1-u} 6 \, dv \, du = 3.$

Nos exercícios 35 a 36, use a transformação$u = y - x, \space v = y$, para avaliar as integrais no paralelogramo$R$ dos vértices$(0,0), \space (1,0), \space (2,1)$, e$(1,1)$ mostrada na figura a seguir.

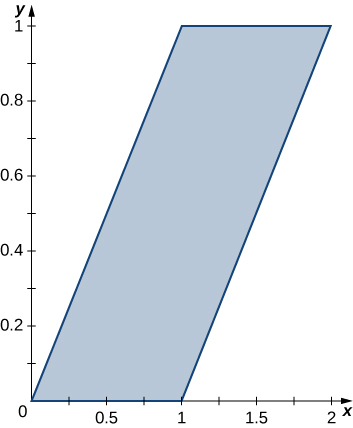
$Um losango com cantos na origem, (1, 0), (1, 1) e (2, 1).$

35. $\displaystyle \iint_R (y - x) \, dA$

36. $\displaystyle \iint_R (y^2 - xy) \, dA$

Answer: $-\frac{1}{4}$

In exercises 37 - 38, use the transformation $y = x = u, \space x + y = v$ to evaluate the integrals on the square $R$ determined by the lines $y = x, \space y = -x + 2, \space y = x + 2$, and $y = -x$ shown in the following figure.

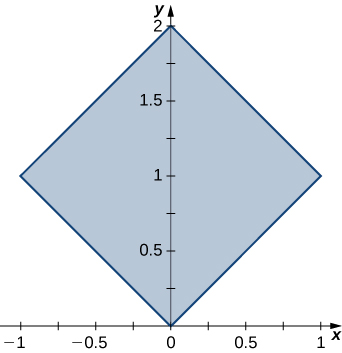
$A square with side lengths square root of 2 rotated 45 degrees with one corner at the origin and another at (1, 1).$

37. $\displaystyle \iint_R e^{x+y} \, dA$

38. $\displaystyle \iint_R \sin (x - y) \, dA$

Resposta: $-1 + \cos 2$

Nos exercícios 39 a 40, use a transformação$x = u, \space 5y = v$ para avaliar as integrais na região$R$ delimitada pela elipse$x^2 + 25y^2 = 1$ mostrada na figura a seguir.

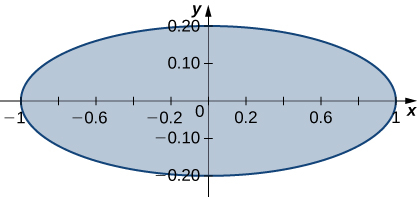
$Uma elipse com centro na origem, eixo maior 2 e menor 0,4.$

39. $\displaystyle \iint_R \sqrt{x^2 + 25y^2} \, dA$

40. $\displaystyle \iint_R (x^2 + 25y^2)^2 \, dA$

Answer: $\frac{\pi}{15}$

In exercises 41 - 42, use the transformation $u = x + y, \space v = x - y$ to evaluate the integrals on the trapezoidal region $R$ determined by the points $(1,0), \space (2,0), \space (0,2)$, and $(0,1)$ shown in the following figure.

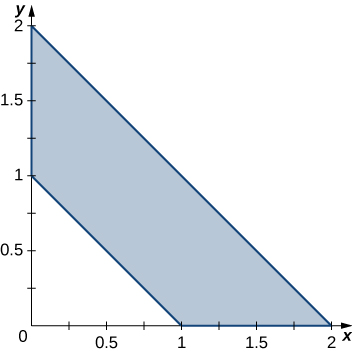
$A trapezoid with corners at (1, 0), (0, 1), (0, 2), and (2, 0).$

41. $\displaystyle \iint_R (x^2 - 2xy + y^2) \space e^{x+y} \, dA$

42. $\displaystyle \iint_R (x^3 + 3x^2y + 3xy^2 + y^3) \, dA$

Resposta: $\frac{31}{5}$

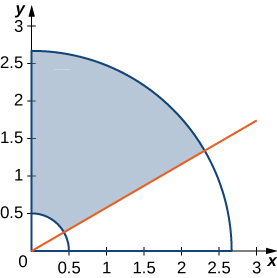
43. O setor circular do anel$R$ delimitado pelos círculos$4x^2 + 4y^2 = 1$ e$9x^2 + 9y^2 = 64$, a linha$x = y \sqrt{3}$ e o$y$ eixo -é mostrado na figura a seguir. Encontre uma transformação$T$ de uma região retangular$S$ no$r\theta$ plano -para a região$R$ no$xy$ plano -. Gráfico$S$.

$No primeiro quadrante, uma seção de um anel descrita por um raio interno de 0,5, raio externo um pouco maior que 2,5 e centro da origem. Há uma linha dividindo esse anel que vem de aproximadamente um ângulo de 30 graus. A porção correspondente a 60 graus está sombreada.$

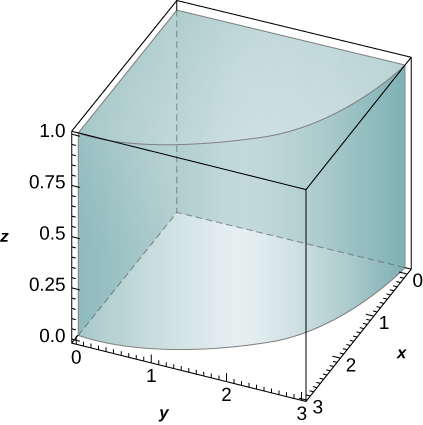
44. O sólido$R$ bounded by the circular cylinder $x^2 + y^2 = 9$ and the planes $z = 0, \space z = 1, \space x = 0$, and $y = 0$ is shown in the following figure. Find a transformation $T$ from a cylindrical box $S$ in $r\theta z$-space to the solid $R$ in $xyz$-space.

$A quarter of a cylinder with height 1 and radius 3. The center axis is the z axis.$

Resposta: $T (r,\theta,z) = (r \space \cos \theta, \space r \space \sin \theta, \space z); \space S = [0,3] \times [0,\frac{\pi}{2}] \times [0,1]$no$r\theta z$ espaço -

45. Mostre que\[\iint_R f \left(\sqrt{\frac{x^2}{3} + \frac{y^2}{3}}\right) dA = 2 \pi \sqrt{15} \int_0^1 f (\rho) \rho \space d\rho, \nonumber \] onde$f$ está uma função contínua ativada$[0,1]$ e$R$ é a região delimitada pela elipse$5x^2 + 3y^2 = 15$.

46. Mostre que\[\iiint_R f \left(\sqrt{16x^2 + 4y^2 + z^2}\right) dV = \frac{\pi}{2} \int_0^1 f (\rho) \rho^2 d\rho, \nonumber \] onde$f$ está uma função contínua ativada$[0,1]$ e$R$ é a região delimitada pelo elipsóide$16x^2 + 4y^2 + z^2 = 1$.

47. [T] Encontre a área da região delimitada pelas curvas$xy = 1, \space xy = 3, \space y = 2x$ e$y = 3x$ usando a transformação$u = xy$$v = \frac{y}{x}$ e. Use um sistema computacional de álgebra (CAS) para representar graficamente as curvas de limite da região$R$.

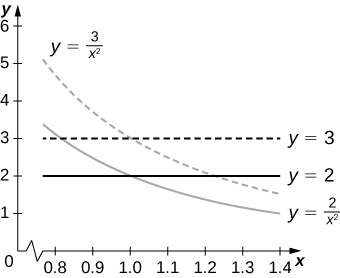
48. [T] Encontre a área da região delimitada pelas curvas$x^2y = 2, \space x^2y = 3, \space y = x$ e$y = 2x$ usando a transformação$u = x^2y$$v = \frac{y}{x}$ e. Use um CAS para representar graficamente as curvas de limite da região$R$.

Resposta

A área de$R$ é$10 - 4\sqrt{6}$; as curvas de limite de$R$ são representadas graficamente na figura a seguir.

$Quatro linhas são desenhadas, a saber, y = 3, y = 2, y = 3/ (x ao quadrado) e y = 2/ (x ao quadrado). As linhas y = 3 e y = 2 são paralelas entre si. As linhas y = 3/ (x ao quadrado) e y = 2/ (x ao quadrado) são curvas que correm um pouco paralelas umas às outras.$

49. Avalie a integral tripla\[\int_0^1 \int_1^2 \int_z^{z+1} (y + 1) \space dx \space dy \space dz \nonumber \] by using the transformation $u = x - z, \space v = 3y$, and $w = \frac{z}{2}$.

50. Evaluate the triple integral \[\int_0^2 \int_4^6 \int_{3z}^{3z+2} (5 - 4y) \space dx \space dy \space dz \nonumber \] by using the transformation $u = x - 3z, \space v = 4y$, and $w = z$.

Answer: $8$

51. A transformation $T : R^2 \rightarrow R^2, \space T (u,v) = (x,y)$ of the form $x = au + bv, \space y = cu + dv$, where $a,b,c$, and $d$ are real numbers, is called linear. Show that a linear transformation for which $ad - bc \neq 0$ maps parallelograms to parallelograms.

52. A transformation $T_{\theta} : R^2 \rightarrow R^2, \space T_{\theta} (u,v) = (x,y)$ of the form $x = u \space \cos \theta - v \space \sin \theta, \space y = u \space \sin \theta + v \space \cos \theta$, is called a rotation angle $\theta$. Show that the inverse transformation of $T_{\theta}$ satisfies $T_{\theta}^{-1} = T_{-\theta}$ where $T_{-\theta}$ is the rotation of angle $-\theta$.

53. [T] Find the region $S$ in the $uv$-plane whose image through a rotation of angle $\frac{\pi}{4}$ is the region $R$ enclosed by the ellipse $x^2 + 4y^2 = 1$. Use a CAS to answer the following questions.

a. Graph the region $S$.

b. Evaluate the integral $\displaystyle \iint_S e^{-2uv} \, du \, dv.$ Round your answer to two decimal places.

54. [T] The transformations $T_i : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space i = 1, . . . , 4,$ defined by $T_1(u,v) = (u,-v), \space T_2 (u,v) = (-u,v), \space T_3 (u,v) = (-u, -v)$, and $T_4 (u,v) = (v,u)$ are called reflections about the $x$-axis, $y$-axis origin, and the line $y = x$, respectively.

a. Find the image of the region $S = \big\{(u,v)\,|\,u^2 + v^2 - 2u - 4v + 1 \leq 0\big\}$ in the $xy$-plane through the transformation $T_1 \circ T_2 \circ T_3 \circ T_4$.

b. Use a CAS to graph $R$.

c. Evaluate the integral $\displaystyle \iint_S \sin (u^2) \, du \, dv$ by using a CAS. Round your answer to two decimal places.

Answer

a. $R = \big\{(x,y)\,|\,y^2 + x^2 - 2y - 4x + 1 \leq 0\big\}$;
b. $R$ is graphed in the following figure;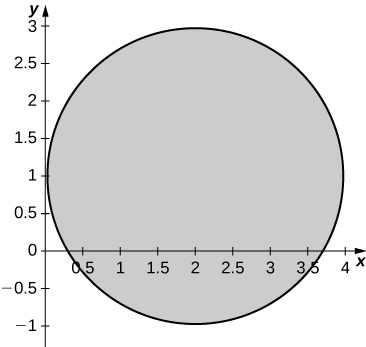

$A circle with radius 2 and center (2, 1).$

c.$3.16$

55. [T] As transformações$T_{k,1,1} : \mathbb{R}^3 \rightarrow \mathbb{R}^3, \space T_{k,1,1}(u,v,w) = (x,y,z)$ da forma$x = ku, \space y = v, \space z = w$, onde$k \neq 1$ há um número real positivo, são chamadas de alongamento se$k > 1$ e compressão se$0 < k < 1$ na$x$ direção -. Use um CAS para avaliar a integral$\displaystyle \iiint_S e^{-(4x^2+9y^2+25z^2)} \, dx \, dy \, dz$ no sólido$S = \big\{(x,y,z) \,|\, 4x^2 + 9y^2 + 25z^2 \leq 1\big\}$ considerando a compressão$T_{2,3,5}(u,v,w) = (x,y,z)$ definida por$x = \frac{u}{2}, \space y = \frac{v}{3}$$z = \frac{w}{5}$ e. Arredonde sua resposta para quatro casas decimais.

56. [T] A transformação$T_{a,0} : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space T_{a,0} (u,v) = (u + av, v)$, onde$a \neq 0$ está um número real, é chamada de distorção na$x$ direção. A transformação$T_{b,0} : R^2 \rightarrow R^2, \space T_{o,b}(u,v) = (u,bu + v)$, onde$b \neq 0$ está um número real, é chamada de distorção na$y$ direção.

a. Encontre transformações$T_{0,2} \circ T_{3,0}$.

b. Encontre a imagem$R$ da região trapezoidal$S$ delimitada por$u = 0, \space v = 0, \space v = 1$ e$v = 2 - u$ através da transformação$T_{0,2} \circ T_{3,0}$.

c. Use um CAS para representar graficamente a imagem$R$ no$xy$ plano.

d. Encontre a área da região$R$ usando a área da região$S$.

Resposta

uma$T_{0,2} \circ T_{3,0}(u,v) = (u + 3v, 2u + 7v)$;.

b. A imagem$S$ é o quadrilátero dos vértices$(0,0), \space (3,7), \space (2,4)$ e$(4,9)$;

c.$S$ é representado graficamente na figura a seguir;

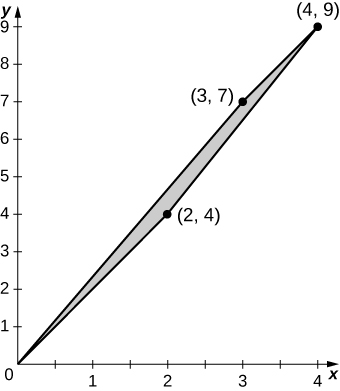
$Uma figura de quatro lados com pontos de origem, (2, 4), (4, 9) e (3, 7).$

Template:ContribOpenStaxCalc