12.4: O produto cruzado

Last updated
Save as PDF

Page ID: 187784

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Calcule o produto cruzado de dois vetores fornecidos.
Use determinantes para calcular um produto cruzado.
Encontre um vetor ortogonal para dois vetores fornecidos.
Determine áreas e volumes usando o produto cruzado.
Calcule o torque de um determinado vetor de força e posição.

Imagine um mecânico girando uma chave para apertar um parafuso. O mecânico aplica uma força na extremidade da chave. Isso cria rotação, ou torque, que aperta o parafuso. Podemos usar vetores para representar a força aplicada pelo mecânico e a distância (raio) do parafuso até a extremidade da chave. Então, podemos representar o torque por um vetor orientado ao longo do eixo de rotação. Observe que o vetor de torque é ortogonal ao vetor de força e ao vetor de raio.

Nesta seção, desenvolvemos uma operação chamada produto cruzado, que nos permite encontrar um vetor ortogonal a dois vetores determinados. O cálculo do torque é uma aplicação importante de produtos cruzados, e examinaremos o torque com mais detalhes posteriormente na seção.

O produto cruzado e suas propriedades

O produto escalar é uma multiplicação de dois vetores que resulta em um escalar. Nesta seção, apresentamos um produto de dois vetores que gera um terceiro vetor ortogonal aos dois primeiros. Considere como podemos encontrar esse vetor. Seja\(\vecs u=⟨u_1,u_2,u_3⟩\) e\(\vecs v=⟨v_1,v_2,v_3⟩\) seja vetores diferentes de zero. Queremos encontrar um vetor\(\vecs w=⟨w_1,w_2,w_3⟩\) ortogonal para ambos\(\vecs u\) e, ou\(\vecs v\) seja, queremos encontrar\(\vecs w\) um vetor ortogonal para\(\vecs u ⋅ \vecs w=0\)\( \vecs v⋅ \vecs w=0\) e. Portanto\(w_1\),\(w_2,\) e\(w_3\) deve satisfazer

\[u_1w_1+u_2w_2+u_3w_3=0 \label{eq1} \]

\[v_1w_1+v_2w_2+v_3w_3=0. \label{eq2} \]

Se multiplicarmos a equação superior por\(v_3\) e a equação inferior por\(u_3\) e subtrairmos, podemos eliminar a variável\(w_3\), que dá

\[(u_1v_3−v_1u_3)w_1+(u_2v_3−v_2u_3)w_2=0. \nonumber \]

Se selecionarmos

\[\begin{align*} w_1 &=u_2v_3−u_3v_2 \\[4pt] w_2 &=−(u_1v_3−u_3v_1), \end{align*}\]

obtemos um possível vetor de solução. Substituindo esses valores de volta nas equações originais (Equações\ ref {eq1} e\ ref {eq2}) dá

\[w_3=u_1v_2−u_2v_1. \nonumber \]

Ou seja, vetor

\[\vecs w=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩ \nonumber \]

é ortogonal a ambos\(\vecs u\) e\(\vecs v\), o que nos leva a definir a seguinte operação, chamada de produto cruzado.

Definição: Produto cruzado

Let\(\vecs u=⟨u_1,u_2,u_3⟩\) and\(\vecs v=⟨v_1,v_2,v_3⟩.\) Then, o produto\(\vecs u×\vecs v\) cruzado é vetor

\[\begin{align} \vecs u×\vecs v &= (u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1) \mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k} \nonumber \\[4pt] &=⟨u_2v_3−u_3v_2,−(u_1v_3−u_3v_1),u_1v_2−u_2v_1⟩. \label{cross}\end{align} \]

Pela forma como nos desenvolvemos\(\vecs u×\vecs v\), deve ficar claro que o produto cruzado é ortogonal a ambos\(\vecs u\)\(\vecs v\) e. No entanto, nunca é demais verificar. Para mostrar que\(\vecs u×\vecs v\) é ortogonal a\(\vecs u\), calculamos o produto escalar de\(\vecs u\)\(\vecs u×\vecs v\) e.

\ [\ begin {align*}\ vecs uω (\ vecs u×\ vecs v) &=⟨u_1, u_2, u_3⋅⟨u_2v_3−u_3v_2, −u_1v_3+u_3v_1, u_1v_2−u_2v_1⟩\\ [4pt] &=u_1 (u_2v_3−u_3v_2) +u_2 (−u_1v_3+u_3v_1) +u_3 (u_1v_2−u_2v_1)\ [4pt]
&=u_1u_2v_3−u_3v_2−u_1u_2v_3+u_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_2v_u_3v_1+u_1u_3v_2−u_2u_3v_1\\ [4pt]
& =( u_1u_2v_3−u_1u_2 v_3) + (−u_1u_3v_2+u_1u_3v_2) + (u_2u_3v_1−u_2u_3v_1)\\ [4pt]
&= 0\ end {alinhamento*}\]

De forma semelhante, podemos mostrar que o produto cruzado também é ortogonal\(\vecs v\) a.

O produto cruzado\(\vecs{a}×\vecs{b}\) (vertical, em rosa) muda à medida que o ângulo entre os vetores\(\vecs{a}\) (azul) e\(\vecs{b}\) (vermelho) muda. O produto cruzado (roxo) é sempre perpendicular a ambos os vetores e tem magnitude zero quando os vetores são paralelos e magnitude máxima\(‖\vecs{a}‖‖\vecs{b}‖\) quando são perpendiculares. (Domínio público; LucasVB).

Exemplo\(\PageIndex{1}\): Finding a Cross Product

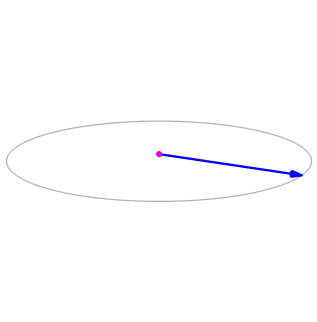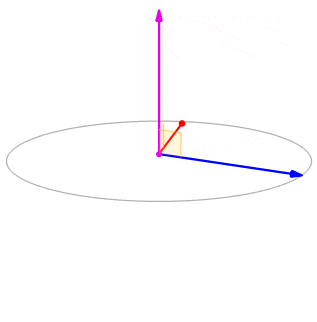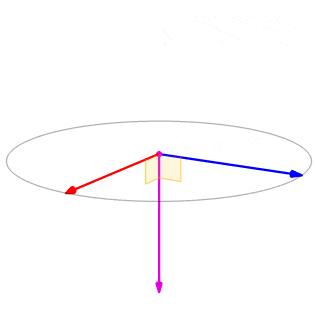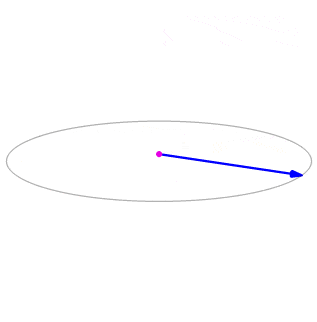
Deixe\(\vecs p=⟨−1,2,5⟩\) e\(\vecs q=⟨4,0,−3⟩\) (Figura\(\PageIndex{1}\)). Encontre\(\vecs p×\vecs q\).

Esta figura é o sistema de coordenadas tridimensional. Ele tem dois vetores na posição padrão. O primeiro vetor é rotulado como “p = <-1, 2, 5 — Figura\(\PageIndex{1}\): Encontrando um produto cruzado para dois vetores fornecidos.

Solução

Substitua os componentes dos vetores na Equação\ ref {cross}:

\[\begin{align*} \vecs p×\vecs q &=⟨−1,2,5⟩×⟨4,0,−3⟩ \\[4pt] &= ⟨p_2q_3−p_3q_2,-(p_1q_3−p_3q_1),p_1q_2−p_2q_1⟩ \\[4pt] &= ⟨2(−3)−5(0),−(−1)(−3)+5(4),(−1)(0)−2(4)⟩ \\[4pt] &= ⟨−6,17,−8⟩.\end{align*}\]

Exercício\(\PageIndex{1}\)

Encontre\(\vecs p×\vecs q\)\(\vecs p=⟨5,1,2⟩\) e\(\vecs q=⟨−2,0,1⟩.\) expresse a resposta usando vetores unitários padrão.

Dica: Use a fórmula\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k}.\)
Resposta: \(\vecs p×\vecs q = \mathbf{\hat i}−9\mathbf{\hat j}+2\mathbf{\hat k}\)

Embora possa não ser óbvio na Equação\ ref {cross}, a direção de\(\vecs u×\vecs v\) é dada pela regra da mão direita. Se segurarmos a mão direita com os dedos apontando na direção de e, em seguida\(\vecs u\), enrolar os dedos em direção ao vetor\(\vecs v\), o polegar aponta na direção do produto cruzado, conforme mostrado na Figura\(\PageIndex{2}\).

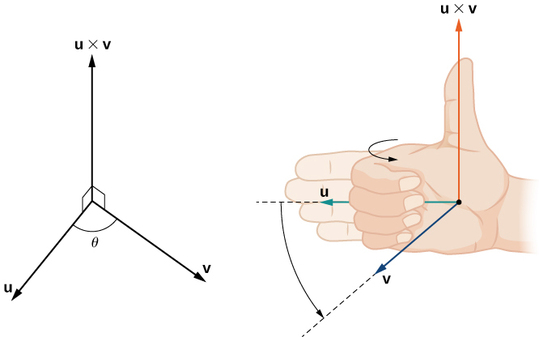
Esta figura tem duas imagens. A primeira imagem tem três vetores com o mesmo ponto inicial. Dois dos vetores são rotulados como “u” e “v.” O ângulo entre u e v é teta. O terceiro vetor é perpendicular a u e v. É rotulado como “u cruz v.” A segunda imagem tem três vetores. Os vetores são rotulados como “u, v e u cross v.” “u cross v” é perpendicular a u e v. Além disso, na imagem desses três vetores está uma mão direita. Os dedos estão na direção de u. Quando a mão está se fechando, a direção dos dedos de fechamento é a direção de v. O polegar está para cima e na direção de “u cruz v.” — Figura\(\PageIndex{2}\): A direção de\( \vecs u× \vecs v\) é determinada pela regra da mão direita.

Observe o que isso significa para a direção de\(\vecs v×\vecs u\). Se aplicarmos a regra da mão direita em\(\vecs v×\vecs u\), começaremos com nossos dedos apontados na direção de e\(\vecs v\), em seguida, enrolamos nossos dedos em direção ao vetor\(\vecs u\). Nesse caso, o polegar aponta na direção oposta de\(\vecs u×\vecs v\). (Experimente!)

Exemplo\(\PageIndex{2}\): Anticommutativity of the Cross Product

Deixe\(\vecs u=⟨0,2,1⟩\)\(\vecs v=⟨3,−1,0⟩\) e. \(\vecs u×\vecs v\)Calcule\(\vecs v×\vecs u\) e faça um gráfico deles.

Esta figura é o sistema de coordenadas tridimensional. Ele tem dois vetores na posição padrão. O primeiro vetor é rotulado como “u = <0, 2, 1 — Figura\(\PageIndex{3}\): Os produtos\(\vecs u×\vecs v\) cruzados estão\(\vecs v×\vecs u\) na mesma direção?

Solução

Nós temos

\(\vecs u×\vecs v=⟨(0+1),−(0−3),(0−6)⟩=⟨1,3,−6⟩\)

\(\vecs v×\vecs u=⟨(−1−0),−(3−0),(6−0)⟩=⟨−1,−3,6⟩.\)

Vemos isso, nesse caso,\(\vecs u×\vecs v=−(\vecs v×\vecs u)\) (Figura\(\PageIndex{4}\)). Provamos isso em geral posteriormente nesta seção.

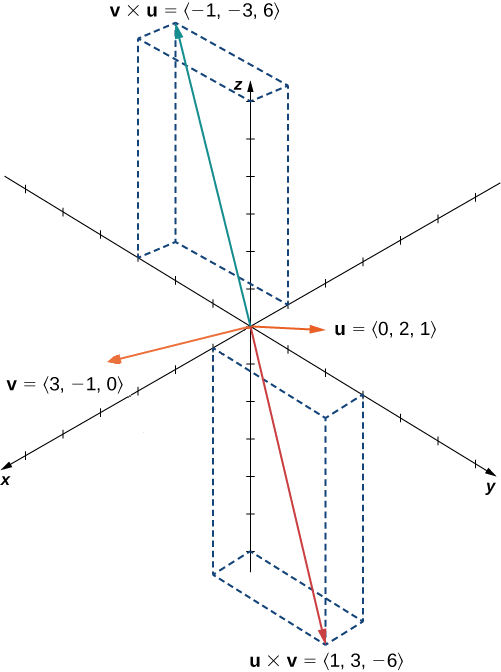
Sistema de coordenadas tridimensional e 4 vetores. Dois dos vetores são rotulados como V e U; os outros dois vetores são os produtos cruzados V cruz U e U cruz V. Ambos são perpendiculares a U e V, mas apontam em direções opostas um do outro. — Figura\(\PageIndex{4}\): Os produtos\(\vecs{u}×\vecs{v}\)\(\vecs{v}×\vecs{u}\) cruzados são ambos ortogonais a\(\vecs{u}\) e\(\vecs{v}\), mas em direções opostas.

Exercício\(\PageIndex{2}\)

Suponha vetores\(\vecs u\) e\(\vecs v\) fique no\(xy\) plano -( o\(z\) componente -de cada vetor é zero). Agora, suponha que os\(y\) componentes\(x\) -\(\vecs u\) e\(y\) -de e o componente -de\(\vecs v\) sejam todos positivos, enquanto o\(x\) componente -de\(\vecs v\) seja negativo. Supondo que os eixos coordenados estejam orientados nas posições usuais, em que direção\(\vecs u×\vecs v\) apontam?

Dica: Lembre-se da regra da mão direita (Figura\(\PageIndex{2}\)).
Resposta: Para cima (a\(z\) direção positiva)

Os produtos cruzados dos vetores unitários padrão\(\mathbf{\hat i}\)\(\mathbf{\hat j}\),, e\(\mathbf{\hat k}\) podem ser úteis para simplificar alguns cálculos, então vamos considerar esses produtos cruzados. Uma aplicação direta da definição mostra que

\[\mathbf{\hat i}×\mathbf{\hat i}=\mathbf{\hat j}×\mathbf{\hat j}=\mathbf{\hat k}×\mathbf{\hat k}=\vecs 0. \nonumber \]

(O produto cruzado de dois vetores é um vetor, então cada um desses produtos resulta no vetor zero, não no escalar\(0\).) Cabe a você verificar os cálculos por conta própria.

Além disso, como o produto cruzado de dois vetores é ortogonal a cada um desses vetores, sabemos que o produto cruzado de\(\mathbf{\hat i}\) e\(\mathbf{\hat j}\) é paralelo\(\mathbf{\hat k}\) a. Da mesma forma, o produto vetorial de\(\mathbf{\hat i}\) e\(\mathbf{\hat k}\) é paralelo a\(\mathbf{\hat j}\), e o produto vetorial de\(\mathbf{\hat j}\) e\(\mathbf{\hat k}\) é paralelo\(\mathbf{\hat i}\) a.

Podemos usar a regra da mão direita para determinar a direção de cada produto. Então nós temos

\ [\ begin {align*}\ mathbf {\ hat i} ×\ mathbf {\ hat j} &=\ mathbf {\ hat k}\\ [4pt]
\ mathbf {\ hat j} ×\ mathbf {\ hat i} &=−\ mathbf {\ hat k}\\ [10pt]
\ mathbf {\ hat j} ×\ mathbf {\ hat k} &=\ mathbf {\ hat i}\\ [4pt]
\ mathbf {\ hat k} ×\ mathbf {\ hat j} &=−\ mathbf {\ hat i}\\ [10 pt]
\ mathbf {\ hat k} ×\ mathbf {\ hat i} &=\ mathbf {\ hat j}\\ [4pt]
\ mathbf {\ hat i} ×\ mathbf {\ hat k} &=−\ mathbf {\ hat j}. \ end {align*}\]

Essas fórmulas serão úteis mais tarde.

Exemplo\(\PageIndex{3}\): Cross Product of Standard Unit Vectors

Encontre\(\mathbf{\hat i} ×(\mathbf{\hat j}×\mathbf{\hat k})\).

Solução

Nós sabemos disso\(\mathbf{\hat j}×\mathbf{\hat k}=\mathbf{\hat i}\). Portanto,\(\mathbf{\hat i}×(\mathbf{\hat j}×\mathbf{\hat k})=\mathbf{\hat i}×\mathbf{\hat i}=\vecs 0.\)

Exercício\(\PageIndex{3}\)

Encontre\((\mathbf{\hat i}×\mathbf{\hat j})×(\mathbf{\hat k}×\mathbf{\hat i}).\)

Dica: Lembre-se da regra da mão direita (Figura\(\PageIndex{2}\)).
Resposta: \(−\mathbf{\hat i}\)

Como vimos, o produto escalar costuma ser chamado de produto escalar porque resulta em um escalar. O produto cruzado resulta em um vetor, por isso às vezes é chamado de produto vetorial. Essas operações são ambas versões da multiplicação vetorial, mas têm propriedades e aplicações muito diferentes. Vamos explorar algumas propriedades do produto cruzado. Nós provamos apenas alguns deles. As provas das outras propriedades são deixadas como exercícios.

Propriedades do produto cruzado

\(\vecs w\)Seja\(\vecs u,\vecs v,\) e seja vetores no espaço e\(c\) seja um escalar.

Propriedade anticomutativa:\[\vecs u×\vecs v=−(\vecs v×\vecs u) \nonumber \]
Propriedade distributiva:\[\vecs u×(\vecs v+\vecs w)=\vecs u×\vecs v+\vecs u×\vecs w \nonumber \]
Multiplicação por uma constante:\[c(\vecs u×\vecs v)=(c\vecs u)×\vecs v=\vecs u×(c\vecs v) \nonumber \]
Produto cruzado do vetor zero:\[\vecs u×\vecs 0=\vecs 0×\vecs u=\vecs 0 \nonumber \]
Produto cruzado de um vetor com ele mesmo:\[\vecs v×\vecs v=\vecs 0 \nonumber \]
Produto triplo escalar:\[\vecs u⋅(\vecs v×\vecs w)=(\vecs u×\vecs v)⋅\vecs w \nonumber \]

Prova

Para a propriedade\(i\), queremos mostrar\(\vecs u×\vecs v=−(\vecs v×\vecs u).\) que temos

\[\begin{align*} \vecs u×\vecs v &=⟨u_1,u_2,u_3⟩×⟨v_1,v_2,v_3⟩ \\[4pt] &=⟨u_2v_3−u_3v_2,−u_1v_3+u_3v_1,u_1v_2−u_2v_1⟩ \\[4pt] &=−⟨u_3v_2−u_2v_3,−u_3v_1+u_1v_3,u_2v_1−u_1v_2⟩ \\[4pt] &=−⟨v_1,v_2,v_3⟩×⟨u_1,u_2,u_3⟩\\[4pt] &=−(\vecs v×\vecs u).\end{align*}\]

Diferente da maioria das operações que vimos, o produto cruzado não é comutativo. Isso faz sentido se pensarmos na regra da mão direita.

Para propriedade\(iv\)., isso decorre diretamente da definição do produto cruzado. Nós temos

\[\vecs u × \vecs 0=⟨u_2(0)−u_3(0),−(u_1(0)−u_3(0)),u_1(0)−u_2(0)⟩=⟨0,0,0⟩=\vecs 0. \nonumber \]

Então, por propriedade i.,\(\vecs 0×\vecs u=\vecs 0\) também. Lembre-se de que o produto escalar de um vetor e o vetor zero são o escalar\(0\), enquanto o produto cruzado de um vetor com o vetor zero é o vetor\(\vecs 0\).

Propriedade\(vi\). se parece com a propriedade associativa, mas observe a mudança nas operações:

\ [\ begin {align*}\ vecs uyang (\ vecs v×\ vecs w) &=u⋅⟨v_2w_3−v_3w_2, −v_1w_3+v_3w_1, v_1w_2−v_2w_1⟩\\ [4pt]
&= u_1 (v_2w_3−v_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w_3w__2) +u_2 (−v_1w_3+v_3w_1) +u_3 (v_1w_2−v_2w_1)\\ [4pt]
&=u_1v_2w_3−u_1v_3w_2−u_2v_1w_3+u_2v_3w_1+u_3v_3v_1+u_3v_3v_1+u_3v_3v_1_v_3v_1w_2−u_3v_2w_1\\ [4pt]
& =( u_2v_3−u_3v _2) w_1+ (u_3v_1−u_1v_3) w_2+ (u_1v_2−u_2v_1) w_3\\ [4pt]
&=⟨u_2v_3−u_3v_2, u_3v_1−u_1v_3, u_1v_2−u_2v_1⇒ ⟨w_1, w_2, w_3⟩ =(\ vecs u×\ vecs v) ≠\ vecs w.\ end {align*}\]

\(\square\)

Exemplo\(\PageIndex{4}\): Using the Properties of the Cross Product

Use as propriedades cruzadas do produto para calcular\((2\mathbf{\hat i}×3\mathbf{\hat j})×\mathbf{\hat j}.\)

Solução

\ [\ begin {align*} (2\ mathbf {\ hat i} ×3\ mathbf {\ hat j}) ×\ mathbf {\ hat j} &=2 (\ mathbf {\ hat i} ×3\ mathbf {\ hat j}) ×\ mathbf {\ hat j}\\ [4pt]
&=2 (3) (\ mathbf {\ hat i} ×\ mathbf {\ hat j}) ×\ mathbf {\ hat j}\\ [4pt]
& =( 6\ mathbf {\ hat k}) ×\ mathbf {\ hat j}\\ [4pt]
&=6 (\ mathbf { \ hat k} ×\ mathbf {\ hat j})\\ [4pt]
&=6 (−\ mathbf {\ hat i}) =−6\ mathbf {\ hat i}. \ end {align*}\]

Exercício\(\PageIndex{4}\)

Use as propriedades do produto cruzado para calcular\((\mathbf{\hat i}×\mathbf{\hat k})×(\mathbf{\hat k}×\mathbf{\hat j}).\)

Dica: \(\vecs u×\vecs v=−(\vecs v×\vecs u)\)
Resposta: \(−\mathbf{\hat k}\)

Até agora, nesta seção, estamos preocupados com a direção do vetor\(\vecs u×\vecs v\), mas não discutimos sua magnitude. Acontece que existe uma expressão simples para a magnitude de\(\vecs u×\vecs v\) envolver as magnitudes de\(\vecs u\) e\(\vecs v\) e e o seno do ângulo entre elas.

Magnitude do produto cruzado

\(\vecs u\)Sejam vetores e\(θ\) sejam o ângulo entre eles.\(\vecs v\) Então,\(‖\vecs u×\vecs v‖=‖\vecs u‖⋅‖\vecs v‖⋅\sin θ.\)

Prova

\(\vecs u=⟨u_1,u_2,u_3⟩\)Sejam vetores e\(θ\) denotem o ângulo entre eles.\(\vecs v=⟨v_1,v_2,v_3⟩\) Então

\ [\ begin {align*} ‖\ vecs u×\ vecs v^2 &= (u_2v_3−u_3v_2) ^2+ (u_3v_1−u_1v_3) ^2+ (u_1v_2−u_2v_1) ^2\\ [4pt]

&=u^2_2v^2_3−3−−2u_2u_3v_2v_3+u^2_3v^2_2+u^2_3v^2_1u_1u_3v_1v_3+u^2_1v^2_3+u^2_1v^2_2u_1u_2v_1v_2v_2+u^2_2v^2_2_2_2u_2u_2u_2u_2u_2v_1v_2_v_2_2_2_2u_1v_2_v_2_2_2u_21\\ [4pt] &=u^2_1v^2_1+u^2_1v^2_2+u^2_1v^2_3+u^2_2v^2_1+u^2_2v ^2_2+u^2_2v^2_3+u^2_3v^2_1+u^2_3v^2_2+u^2_3v^2_3− (u^2_1v^2_1+u^2_2_2+u^2_3v^2_3+2u_1u_2v_1v_1v_1v_1v_1v_1v_1v_1v_1v_1v_1v_1v_1v_1v_1v_1v_1v_v_1v_1v2+2u_1u_3v_1v_3+2u_2u_3v_2v_3)\\ [4pt]
& =( u^2_1+u^2_2+u^2_3) (v^2_1+v^2_2+v^2_3) − (u_1v_1+u_2v_2+u_3_3+u_3_3) v_3) ^2\\ [4pt]
&=‖\ vecs u^2‖\ vecs v^2− (\ vecs u∞\ vecs v) ^2\\ [4pt]
&=‖\ vecs u^2‖\ vecs v^2−‖\ vecs u^2‖\ vecs v^2\ cos^2θ\\ [4pt]
&=‖\ vecs u^2‖\ vecs v^2 (1−\ cos^2θ)\\ [4pt]
&=‖\ vecs u^2‖\ vecs v^2 (\ sin^2θ). \ end {align*}\ nonumber\]

Tomando raízes quadradas e observando que,\(\sqrt{\sin^2θ}=\sinθ\) para\(0≤θ≤180°,\) nós, temos o resultado desejado:

\[‖\vecs u×\vecs v‖=‖\vecs u‖‖\vecs v‖ \sin θ. \nonumber \]

□

Essa definição do produto cruzado nos permite visualizar ou interpretar o produto geometricamente. É claro, por exemplo, que o produto cruzado é definido apenas para vetores em três dimensões, não para vetores em duas dimensões. Em duas dimensões, é impossível gerar um vetor simultaneamente ortogonal a dois vetores não paralelos.

Exemplo\(\PageIndex{5}\): Calculating the Cross Product

Use “Magnitude do Produto Cruzado” para encontrar a magnitude do produto cruzado de\(\vecs u=⟨0,4,0⟩\)\(\vecs v=⟨0,0,−3⟩\) e.

Solução

Nós temos

\ [\ begin {align*} ‖\ vecs u×\ vecs v‖ &= ‖\ vecs u⋅‖\ vecs vwitz\ sinθ\\ [4pt]
&=\ sqrt {0^2+4^2+0^2} ≠\ sqrt {0^2+0^2+ (−3) ^2} □\ sin {\ dfrac {π} {2}}}\\ [4pt]
&=4 (3) (1) =12\ end {align*}\]

Exercício\(\PageIndex{5}\)

Use “Magnitude do Produto Cruzado” para encontrar a magnitude de\(\vecs u×\vecs v\), onde\(\vecs u=⟨−8,0,0⟩\)\(\vecs v=⟨0,2,0⟩\) e.

Dica: Vetores\(\vecs u\) e\(\vecs v\) são ortogonais.
Resposta: 16

Determinantes e o produto cruzado

Usar a Equação\ ref {cross} para encontrar o produto cruzado de dois vetores é simples e apresenta o produto cruzado na forma de componente útil. A fórmula, no entanto, é complicada e difícil de lembrar. Felizmente, temos uma alternativa. Podemos calcular o produto cruzado de dois vetores usando a notação determinante.

Um\(2×2\) determinante é definido por

\[\begin{vmatrix}a_1 & b_1\\a_2 & b_2\end{vmatrix} =a_1b_2−b_1a_2. \nonumber \]

Por exemplo,

\[\begin{vmatrix}3 & −2\\5 & 1\end{vmatrix} =3(1)−5(−2)=3+10=13. \nonumber \]

Um\(3×3\) determinante é definido em termos de\(2×2\) determinantes da seguinte forma:

\[\begin{vmatrix}a_1 & a_2 & a_3\\b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix}=a_1\begin{vmatrix}b_2 & b_3\\c_2 & c_3\end{vmatrix}−a_2\begin{vmatrix}b_1 & b_3\\c_1 & c_3\end{vmatrix}+a_3\begin{vmatrix}b_1 & b_2\\c_1 & c_2\end{vmatrix}.\label{expandEqn} \]

A equação\ ref {expandeQn} é chamada de expansão do determinante ao longo da primeira linha. Observe que os multiplicadores de cada um dos\(2×2\) determinantes no lado direito dessa expressão são as entradas na primeira linha do\(3×3\) determinante. Além disso, cada um dos\(2×2\) determinantes contém as entradas do\(3×3\) determinante que permaneceriam se você riscasse a linha e a coluna que contêm o multiplicador. Assim, para o primeiro termo à direita,\(a_1\) é o multiplicador, e o\(2×2\) determinante contém as entradas que restam se você riscar a primeira linha e a primeira coluna do\(3×3\) determinante. Da mesma forma, para o segundo termo, o multiplicador é\(a_2\), e o\(2×2\) determinante contém as entradas que permanecem se você riscar a primeira linha e a segunda coluna do\(3×3\) determinante. Observe, no entanto, que o coeficiente do segundo termo é negativo. O terceiro termo pode ser calculado de forma semelhante.

Exemplo\(\PageIndex{6}\): Using Expansion Along the First Row to Compute a \(3×3\) Determinant

Avalie o determinante\(\begin{vmatrix}2 & 5 &−1\\−1 & 1 & 3\\−2 & 3 & 4\end{vmatrix}\).

Solução

Nós temos

\ [\ begin {align*}\ begin {vmatrix} 2 e 5 & −1\\ −1 & 1 & 3\\ −2 e 3 e 4\ end {vmatrix} &=2\ begin {vmatrix} 1 e 3\\ 3 e 4\ end {vmatrix} −5\ begin {vmatrix} −1 e 3\\ −2 e 4\ end {vmatrix} −1\ begin {vmatrix} −1\ begin {vmatrix} −1\ begin {vmatrix} −1 matriz} −1 e 1\\ −2 e 3\ end {vmatrix}\\ [4pt]
&=2 (4−9) −5 (−4+6) −1 (−3+2 )\\ [4pt]
&= 2 (−5) −5 (2) −1 (−1) =−10−10+1\\ [4pt]
&=−19\ end {align*}\]

Exercício\(\PageIndex{6}\)

Avalie o determinante\(\begin{vmatrix}1 & −2 & −1\\3 & 2 & −3\\1 & 5 & 4\end{vmatrix}\).

Dica: Expanda ao longo da primeira linha. Não se esqueça que o segundo termo é negativo!
Resposta: 40

Tecnicamente, os determinantes são definidos apenas em termos de matrizes de números reais. No entanto, a notação determinante fornece um dispositivo mnemônico útil para a fórmula do produto cruzado.

Regra: Produto cruzado calculado por um determinante

Deixem\(\vecs u=⟨u_1,u_2,u_3⟩\) e\(\vecs v=⟨v_1,v_2,v_3⟩\) sejam vetores. Em seguida, o produto cruzado\(\vecs u×\vecs v\) é dado por

\[\vecs u×\vecs v=\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3\end{vmatrix}=\begin{vmatrix}u_2 & u_3\\v_2 & v_3\end{vmatrix}\mathbf{\hat i}−\begin{vmatrix}u_1 & u_3\\v_1 & v_3\end{vmatrix}\mathbf{\hat j}+\begin{vmatrix}u_1 & u_2\\v_1 & v_2\end{vmatrix}\mathbf{\hat k}. \nonumber \]

Exemplo\(\PageIndex{7}\): Using Determinant Notation to find \(\vecs p×\vecs q\)

Deixe\(\vecs p=⟨−1,2,5⟩\)\(\vecs q=⟨4,0,−3⟩\) e. Encontre\(\vecs p×\vecs q\).

Solução

Configuramos nosso determinante colocando os vetores unitários padrão na primeira linha, os componentes da\(\vecs u\) na segunda linha e os componentes da\(\vecs v\) na terceira linha. Então, nós temos

\ [\ begin {align*}\ vecs p×\ vecs q &=\ begin {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\\ −1 e 2 e 5\\ 4 e 0 & −3\ end {vmatrix} =\ begin {vmatrix} 2 e 5\\ 0 & −3\ end {vmatrix}\ mathbf {\ hat i} −\ begin {vmatrix} −1 e 5\\ 4 & −3\ end {vmatrix}\ mathbf {\ hat j} +\ begin {vmatrix} − 1 e 2\\ 4 e 0\ end {vmatrix}\ mathbf {\ hat k}\\ [4pt]
&= (−6−0)\ mathbf {\ hat i} − (3−20)\ mathbf {\ hat j} + (0−8)\ mathbf {\ hat k}\\ [4pt]
&=−6\ mathbf {\ hat is} +17\ mathbf {\ hat j} −8\ mathbf {\ hat k}. \ end {align*}\]

Observe que essa resposta confirma o cálculo do produto cruzado no Exemplo\(\PageIndex{1}\).

Exercício\(\PageIndex{7}\)

Use a notação determinante para encontrar\(\vecs a×\vecs b\), onde\(\vecs a=⟨8,2,3⟩\) e\(\vecs b=⟨−1,0,4⟩.\)

Dica: Calcule o determinante\(\begin{vmatrix}\mathbf{\hat i} \mathbf{\hat j} \mathbf{\hat k}\\8 & 2 & 3\\−1 & 0 & 4\end{vmatrix}\).
Resposta: \(\vecs a×\vecs b = 8\mathbf{\hat i}−35\mathbf{\hat j}+2\mathbf{\hat k}\)

Usando o produto cruzado

O produto cruzado é muito útil para vários tipos de cálculos, incluindo encontrar um vetor ortogonal a dois vetores determinados, computar áreas de triângulos e paralelogramos e até mesmo determinar o volume da forma geométrica tridimensional feita de paralelogramos conhecida como paralelepípedo. Os exemplos a seguir ilustram esses cálculos.

Exemplo\(\PageIndex{8}\): Finding a Unit Vector Orthogonal to Two Given Vectors

Deixe\(\vecs a=⟨5,2,−1⟩\)\(\vecs b=⟨0,−1,4⟩\) e. Encontre um vetor unitário ortogonal para ambos\(\vecs a\)\(\vecs b\) e.

Solução

O produto cruzado\(\vecs a×\vecs b\) é ortogonal tanto para os vetores\(\vecs a\) quanto para\(\vecs b\). Podemos calculá-lo com um determinante:

\ [\ begin {align*}\ vecs a×\ vecs b &=\ begin {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\\ 5 e 2 & −1\\ 0 & −1 e 4\ end {vmatrix} =\ begin {vmatrix} 2 & −1\\ −1 & −1\\ −1 & −1\\ −1 & −1\\ −1 & 4\ end {vmatrix}\ mathbf {\ hat i} −\ begin {vmatrix} 5 & −1\\ 0 e 4\ end {vmatrix}\ mathbf {\ hat j} +\ begin {vmatrix} 5 & 2\\ 0 & −1\ end {vmatrix}\ mathbf {\ hat k}\\ [4pt]
& =( 8−1)\ mathbf {\ hat i} − (20−0)\ mathbf {\ hat j} + (−5−0)\ mathbf {\ hat k}\\ [4pt]
&=7\ mathbf {\ hat i} −20\ mathbf {\ hat j} −5\ mathbf {\ hat k}. \ end {align*}\ nonumber\]

Normalize esse vetor para encontrar um vetor unitário na mesma direção:

\(\|\vecs a×\vecs b\|=\sqrt{(7)^2+(−20)^2+(−5)^2}=\sqrt{474}\).

Assim,\(\left\langle\dfrac{7}{\sqrt{474}},\dfrac{−20}{\sqrt{474}},\dfrac{−5}{\sqrt{474}}\right\rangle\) é um vetor unitário ortogonal a\(\vecs a\)\(\vecs b\) e.

Simplificado, esse vetor se torna\(\left\langle\dfrac{7\sqrt{474}}{474},\dfrac{−10\sqrt{474}}{237},\dfrac{−5\sqrt{474}}{474}\right\rangle\).

Exercício\(\PageIndex{8}\)

Encontre um vetor unitário ortogonal para ambos\(\vecs a\) e\(\vecs b\), onde\(\vecs a=⟨4,0,3⟩\) e\(\vecs b=⟨1,1,4⟩.\)

Dica: Normalize o produto cruzado.
Resposta: \(\left\langle\dfrac{−3}{\sqrt{194}},\dfrac{−13}{\sqrt{194}},\dfrac{4}{\sqrt{194}}\right\rangle\)ou, simplificado como\(\left\langle\dfrac{−3\sqrt{194}}{194},\dfrac{−13\sqrt{194}}{194},\dfrac{2\sqrt{194}}{97}\right\rangle\)

Para usar o produto cruzado para calcular áreas, declaramos e provamos o seguinte teorema.

Área de um paralelogramo

Se localizarmos vetores\(\vecs u\) e\(\vecs v\) formarmos lados adjacentes de um paralelogramo, a área do paralelogramo será dada por\(‖\vecs u×\vecs v‖\) (Figura\(\PageIndex{5}\)).

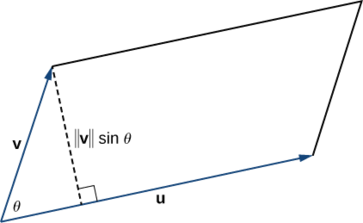
Essa figura é um paralelogramo. Um lado é representado por um vetor rotulado “v.” O segundo lado, a base, tem o mesmo ponto inicial do vetor v e é rotulado como “u”. O ângulo entre u e v é teta. Além disso, um segmento de linha perpendicular é desenhado do ponto terminal de v até o vetor u. É rotulado como “|v|sin (teta)”. — Figura\(\PageIndex{5}\): O paralelogramo com lados adjacentes\(\vecs u\) e\(\vecs v\) tem base\(‖\vecs u‖\) e altura\(‖\vecs v‖\sin θ\).

Prova

Mostramos que a magnitude do produto cruzado é igual à base vezes a altura do paralelogramo.

\[\begin{align*} \text{Area of a parallelogram} &= \text{base} × \text{height} \\[4pt] &=‖\vecs u‖(‖\vecs v‖\sin θ) \\[4pt] &=‖\vecs u×\vecs v‖ \end{align*}\]

□

Exemplo\(\PageIndex{9}\): Finding the Area of a Triangle

Seja\(P=(1,0,0),Q=(0,1,0),\) e\(R=(0,0,1)\) seja os vértices de um triângulo (Figura\(\PageIndex{6}\)). Encontre sua área.

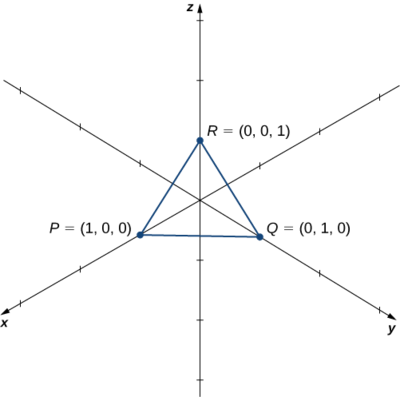
Esta figura é o sistema de coordenadas tridimensional. Tem um triângulo desenhado no primeiro octante. Os vértices do triângulo são os pontos P (1, 0, 0); Q (0, 1, 0); e R (0, 0, 1). — Figura\(\PageIndex{6}\): Encontrando a área de um triângulo usando o produto cruzado.

Solução

Nós temos\(\vecd{PQ}=⟨0−1,1−0,0−0⟩=⟨−1,1,0⟩\)\(\vecd{PR}=⟨0−1,0−0,1−0⟩=⟨−1,0,1⟩\) e. A área do paralelogramo com lados adjacentes\(\vecd{PQ}\) e\(\vecd{PR}\) é dada por\(∥\vecd{PQ}×\vecd{PR}∥\):

\ [\ begin {align*}\ vecd {PQ}\ times\ vecd {PR} &=\ begin {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\\ −1 e 1 & 0\\ −1 e 0 & 1\ end {vmatrix}\\ [4pt]
&= (1−0)\ mathbf {\ hat i} − (−1−0)\ mathbf {\ hat j} + (0− (−1))\ mathbf {\ hat k}\\ [4pt]
&=\ mathbf {\ O que é} +\ mathbf {\ hat j} +\ mathbf {\ hat k}\\ [10pt]
\ vecd {PQ} ×\ vecd {PR} &=⟨1,1,1\\ [4pt]
&=\ sqrt {1^2+1^2+1^2}\\ [4pt]
&=\ sqrt {3}. \ end {align*}\ nonumber\]

A área de\(ΔPQR\) é metade da área do paralelogramo ou\(\sqrt{3}/2 \, \text{units}^2\).

Exercício\(\PageIndex{9}\)

Encontre a área do paralelogramo\( PQRS\) com os vértices\( P(1,1,0)\)\(Q(7,1,0)\)\(R(9,4,2)\),,\( S(3,4,2)\) e.

Dica: Desenhe o paralelogramo e identifique dois vetores que formam lados adjacentes do paralelogramo.
Resposta: \(6\sqrt{13}\, \text{units}^2\)

O produto triplo escalar

Como o produto cruzado de dois vetores é um vetor, é possível combinar o produto escalar e o produto cruzado. O produto escalar de um vetor com o produto cruzado de dois outros vetores é chamado de produto escalar triplo porque o resultado é um escalar.

Definição: Produto escalar triplo

O produto escalar triplo dos vetores\( \vecs u\),\( \vecs v,\) e\(\vecs w\) é

\[ \vecs u⋅( \vecs v× \vecs w). \nonumber \]

Calculando um produto escalar triplo

O produto escalar triplo dos vetores

\[ \vecs u=u_1 \mathbf{\hat i}+u_2 \mathbf{\hat j}+u_3\mathbf{\hat k} \nonumber \]

\[ \vecs v=v_1\mathbf{\hat i}+v_2\mathbf{\hat j}+v_3\mathbf{\hat k} \nonumber \]

\[ \vecs w=w_1 \mathbf{\hat i}+w_2\mathbf{\hat j}+w_3\mathbf{\hat k} \nonumber \]

é o determinante da\(3×3\) matriz formada pelos componentes dos vetores:

\[ \vecs u⋅( \vecs v× \vecs w)=\begin{vmatrix}u_1 & u_2 & u_3\\v_1 & v_2 & v_3\\w_1 & w_2 & w_3\end{vmatrix}. \label{triple2} \]

Prova

O cálculo é simples.

\ [\ begin {align*}\ vecs uyang (\ vecs v×\ vecs w) &=⟨u_1, u_2, u_3⋅⟨v_2w_3−v_3w_2, −v_1w_3+v_3w_1, v_1w_2−v_2w_1⟩\\ [4pt] &=u_1 (v_2w_3−v_3w_2) +u_2 (−v_1w_3+v_3w_1) +u_3 (v_1w_2−v_2w_1)\\ [4pt]
&=u_1 (v_2w_3−v_3w_2) −u_2 (v_1w_3−v_3w_3−v_3 w_1) +u_3 (v_1w_2−v_2w_1)\\ [4pt]
&=\ begin {matriz} u_ 1 & u_2 e u_3\\ v_1 e v_2 e v_3\\ w_1 e w_2 e w_3\ end {vmatrix}. \ end {align*}\ nonumber\]

□

Exemplo\(\PageIndex{10}\): Calculating the Triple Scalar Product

Deixe\(\vecs u=⟨1,3,5⟩,\,\vecs v=⟨2,−1,0⟩\)\(\vecs w=⟨−3,0,−1⟩\) e. Calcule o produto escalar triplo\(\vecs u⋅(\vecs v×\vecs w).\)

Solução

Aplique a Equação\ ref {triple2} diretamente:

\ [\ begin {align*}\ vecs uρ (\ vecs v×\ vecs w) &=\ begin {vmatrix} 1 e 3 & 5\\ 2 & −1 & 0\\ −3 e 0 & −1\ end {vmatrix}\\ [4pt]
&=1\ begin {vmatrix} −1 & 0\\ 0 & −1\ end {vmatrix} −3\ begin {vmatrix} 2 e 0\\ −3 & −1\ end {vmatrix} +5\ begin {vmatrix} 2 & −1\\ −3 e 0\ end { matriz}\\ [4pt]
& =( 1−0) −3 (−2−0) +5 (0−3)\\ [4pt]
&=1+6−15=−8. \ end {align*}\ nonumber\]

Exercício\(\PageIndex{10}\)

Calcule o produto escalar triplo\(\vecs a⋅(\vecs b×\vecs c),\) onde\(\vecs a=⟨2,−4,1⟩, \vecs b=⟨0,3,−1⟩\), e\(\vecs c=⟨5,−3,3⟩.\)

Dica: Coloque os vetores como as linhas de uma\(3×3\) matriz e calcule o determinante.
Resposta: \(17\)

Quando criamos uma matriz a partir de três vetores, devemos ter cuidado com a ordem na qual listamos os vetores. Se os listarmos em uma matriz em uma ordem e depois reorganizarmos as linhas, o valor absoluto do determinante permanecerá inalterado. No entanto, cada vez que duas linhas trocam de lugar, o sinal de mudança determinante:

\(\begin{vmatrix}a_1 & a_2 & a_3\\b_1 & b_2 & b_3\\c_1 & c_2 & c_3\end{vmatrix}=d \quad\quad \begin{vmatrix}b_1 & b_2 & b_3\\a_1 & a_2 & a_3\\c_1 & c_2 & c_3\end{vmatrix}=−d \quad\quad \begin{vmatrix}b_1 & b_2 & b_3\\c_1 & c_2 & c_3\\a_1 & a_2 & a_3\end{vmatrix}=d \quad\quad \begin{vmatrix}c_1 & c_2 & c_3\\b_1 & b_2 & b_3\\a_1 & a_2 & a_3\end{vmatrix}=−d\)

Verificar esse fato é simples, mas bastante confuso. Vamos dar uma olhada nisso com um exemplo:

\ [\ begin {align*}\ begin {vmatrix} 1 e 2 e 1\\ −2 e 0 & 3\\ 4 e 1 & −1\ end {vmatrix} &=\ begin {vmatrix} 0 e 3\\ 1 & −1\ end {vmatrix} −2\ begin {vmatrix} −2 e 3\\ 4 & −1\ end {vmatrix} +\ begin {vmatrix} −2 e 3\\ 4 & −1\ end {vmatrix} +\ begin {vmatrix} −2 e 0\\ 4 e 1\ end {vmatrix}\\ [4pt]
& =( 0−3) −2 (2−12) + (−2−0)\\ [4pt]
&=−3+20−2=15. \ end {align*}\ nonumber\]

Trocando as duas linhas superiores, temos

\ [\ begin {align*}\ begin {vmatrix} −2 e 0 & 3\\ 1 & 2 & 1\\ 4 & 1 & −1\ end {vmatrix} &=-2\ begin {vmatrix} 2 e 1\\ 1 & −1\ end {vmatrix} +3\ begin {vmatrix} 1 e 2\\ 4 e 1\ end {vmatrix}\\ [4pt]
−2 (−2−1) +3 (1−8)\\ [4pt]
&=6−21=−15. \ end {align*}\ nonumber\]

Reorganizar vetores nos produtos triplos é equivalente a reordenar as linhas na matriz do determinante. Let\(\vecs u=u_1\mathbf{\hat i}+u_2\mathbf{\hat j}+u_3\mathbf{\hat k}, \vecs v=v_1\mathbf{\hat i}+v_2\mathbf{\hat j}+v_3\mathbf{\hat k},\) and\(\vecs w=w_1\mathbf{\hat i}+w_2\mathbf{\hat j}+w_3\mathbf{\hat k}.\) Applicing Note, temos

\[\vecs u⋅(\vecs v×\vecs w)=\begin{vmatrix}u_1 & u_2 & u_3\\v_1 & v_2 & v_3\\w_1 & w_2 & w_3\end{vmatrix} \nonumber \]

\[\vecs u⋅(\vecs w×\vecs v)=\begin{vmatrix}u_1 & u_2 & u_3\\w_1 & w_2 & w_3\\v_1 & v_2 & v_3\end{vmatrix}. \nonumber \]

Podemos obter o determinante para calcular\(\vecs u⋅(\vecs w×\vecs v)\) trocando as duas linhas inferiores de\(\vecs u⋅(\vecs v×\vecs w).\) Portanto,\(\vecs u⋅(\vecs v×\vecs w)=−\vecs u⋅(\vecs w×\vecs v).\)

Seguir esse raciocínio e explorar as diferentes maneiras pelas quais podemos trocar variáveis no produto escalar triplo resultam nas seguintes identidades:

\ [\ begin {align}\ vecs uⅡ (\ vecs v×\ vecs w) &=−\ vecs u(\ vecs w×\ vecs v)\\ [10pt]
\ vecs u94 (\ vecs v×\ vecs w) &=\ vecs v𝑦 (\ vecs w×\ vecs u) =\ vecs w8.4 (\ vecs u×\ vecs (v). \ end {align}\ nonumber\]

Seja\(\vecs u\) e\(\vecs v\) seja dois vetores na posição padrão. Se\(\vecs u\) e não\(\vecs v\) forem múltiplos escalares um do outro, esses vetores formam lados adjacentes de um paralelogramo. Vimos em Note que a área desse paralelogramo é\(‖\vecs u×\vecs v‖\). Agora, suponha\(\vecs w\) que adicionemos um terceiro vetor que não esteja no mesmo plano de\(\vecs u\) e\(\vecs v\), mas ainda compartilhe o mesmo ponto inicial. Então, esses vetores formam três bordas de um paralelepípedo, um prisma tridimensional com seis faces, cada uma delas sendo paralelogramos, conforme mostrado na Figura\(\PageIndex{7}\). O volume desse prisma é o produto da altura da figura e da área de sua base. O produto escalar triplo de\(\vecs u,\vecs v,\) e\(\vecs w\) fornece um método simples para calcular o volume do paralelepípedo definido por esses vetores.

Volume de um paralelepípedo

O volume de um paralelepípedo com bordas adjacentes dado pelos vetores\(\vecs u,\vecs v\), e\(\vecs w\) é o valor absoluto do produto escalar triplo (Figura\(\PageIndex{7}\)):

\[V=||\vecs u⋅(\vecs v×\vecs w)||. \nonumber \]

Observe que, como o nome indica, o produto escalar triplo produz um escalar. A fórmula de volume que acabamos de apresentar usa o valor absoluto de uma quantidade escalar.

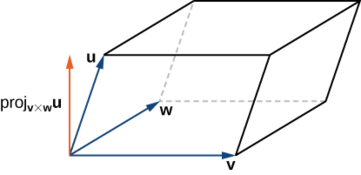
Esta figura é um paralelepídeo, um paralelogramo tridimensional. Três dos lados são representados com vetores. A base tem vetores v e w. O lado vertical tem vetor u. Todos os três vetores têm o mesmo ponto inicial. Um vetor perpendicular é desenhado a partir desse ponto comum. É rotulado como “proj sub (v x w) u.” — Figura\(\PageIndex{7}\): A altura do paralelepípedo é dada por\(\|\text{proj}_{\vecs v×\vecs w}\vecs u\|.\)

Prova

A área da base do paralelepípedo é dada por\(‖\vecs v×\vecs w‖.\) A altura da figura é dada por\(\|\text{proj}_{\vecs v×\vecs w}\vecs u\|.\) O volume do paralelepípedo é o produto da altura e da área da base, então temos

\ [\ begin {align*} V &=\ text {proj} _ {\ vecs v×\ vecs w}\ vecs u‖\ vecs v×\ vecs w‖\\ [4pt]
&=\ dfrac {\ vecs u(\ vecs v×\ vecs w)} {‖\ vecs v×\ vecs w‖}\ ‖ vecs v×\ vecs w‖\\ [4pt]
&=\ |\ vecs uⅡ (\ vecs v×\ vecs w)\ |. \ end {align*}\]

□

Exemplo\(\PageIndex{11}\): Calculating the Volume of a Parallelepiped

Deixe\(\vecs u=⟨−1,−2,1⟩,\vecs v=⟨4,3,2⟩,\)\(\vecs w=⟨0,−5,−2⟩\) e. Encontre o volume do paralelepípedo com bordas\(\vecs u,\vecs v\) adjacentes e\(\vecs w\) (Figura\(\PageIndex{8}\)).

Esta figura é o sistema de coordenadas tridimensional. Ele tem três vetores na posição padrão. Os vetores são u = <-1, -2, 1 — Figura\(\PageIndex{8}\)

Solução

Nós temos

\ [\ begin {align*}\ vecs uρ (\ vecs v×\ vecs w) &=\ begin {vmatrix} −1 & −2 e 1\\ 4 e 3 & 2\\ 0 & −5 & −2\ end {vmatrix}\\ [4pt]
&= (−1)\ begin {vmatrix} 3 e 2\\ −5 e −2\ end {vmatrix} +2\ begin {vmatrix} 4 e 2\\ 0 & −2\ end {vmatrix} +\ begin {vmatrix} 4 e 3\\ 0 & −5\ end { matriz}\\ [4pt]
& =( −1) (−6+10) +2 (−8−0) + (−20−0)\\ [4pt]
&=−4−16−20\\ [4pt]
&=−40. \ end {align*}\]

Assim, o volume do paralelepípedo é de\(|−40|=40\) unidades ³

Exercício\(\PageIndex{11}\)

Encontre o volume do paralelepípedo formado pelos vetores\(\vecs a=3\mathbf{\hat i}+4\mathbf{\hat j}−\mathbf{\hat k}, \vecs b=2\mathbf{\hat i}−\mathbf{\hat j}−\mathbf{\hat k},\) e\(\vecs c=3\mathbf{\hat j}+\mathbf{\hat k}.\)

Dica: Calcule o produto escalar triplo encontrando um determinante.
Resposta: \(8\)unidades ³

Aplicações do produto cruzado

O produto cruzado aparece em muitas aplicações práticas em matemática, física e engenharia. Vamos examinar algumas dessas aplicações aqui, incluindo a ideia de torque, com a qual começamos esta seção. Outras aplicações aparecem em capítulos posteriores, particularmente em nosso estudo de campos vetoriais, como campos gravitacionais e eletromagnéticos (Introdução ao cálculo vetorial).

Exemplo\(\PageIndex{12}\): Using the Triple Scalar Product

Use o produto escalar triplo para mostrar que os vetores e\(\vecs w=⟨1,−1,3⟩\) são coplanares\(\vecs u=⟨2,0,5⟩,\vecs v=⟨2,2,4⟩\), ou seja, mostram que esses vetores estão no mesmo plano.

Solução

Comece calculando o produto escalar triplo para encontrar o volume do paralelepípedo definido por\(\vecs u,\vecs v,\) e\(\vecs w\):

\ [\ begin {align*}\ vecs uρ (\ vecs v×\ vecs w) &=\ begin {vmatrix} 2 & 0 & 5\\ 2 e 2 & 4\\ 1 & −1 e 3\ end {vmatrix}\\ [4pt]
&= [2 (2) (3) + (0) (4) (1) +5 (2) (−1)] [5 (2) (1) + (2) (4) (−1) + (0) (2) (3)]\\ [4pt]
&=2−2 =0. \ end {align*}\]

O volume do paralelepípedo é de\(0\) unidades ³, então uma das dimensões deve ser zero. Portanto, os três vetores estão todos no mesmo plano.

Exercício\(\PageIndex{12}\)

Os vetores\(\vecs a=\mathbf{\hat i}+\mathbf{\hat j}−\mathbf{\hat k}, \vecs b=\mathbf{\hat i}−\mathbf{\hat j}+\mathbf{\hat k},\) são\(\vecs c=\mathbf{\hat i}+\mathbf{\hat j}+\mathbf{\hat k}\) coplanares?

Dica: Calcule o produto escalar triplo.
Resposta: Não, o produto escalar triplo é\(−4≠0,\) que os três vetores formam as bordas adjacentes de um paralelepípedo. Eles não são coplanares.

Exemplo\(\PageIndex{13}\): Finding an Orthogonal Vector

Somente um único plano pode passar por qualquer conjunto de três pontos não colineares. Encontre um vetor ortogonal ao plano contendo pontos\(P=(9,−3,−2),Q=(1,3,0),\) e\(R=(−2,5,0).\)

Solução

O plano deve conter vetores\(\vecd{PQ}\) e\(\vecd{QR}\):

\(\vecd{PQ}=⟨1−9,3−(−3),0−(−2)⟩=⟨−8,6,2⟩\)

\(\vecd{QR}=⟨−2−1,5−3,0−0⟩=⟨−3,2,0⟩.\)

O produto cruzado\(\vecd{PQ}×\vecd{QR}\) produz um vetor ortogonal para ambos\(\vecd{PQ}\)\(\vecd{QR}\) e. Portanto, o produto cruzado é ortogonal ao plano que contém esses dois vetores:

\ [\ begin {align*}\ vecd {PQ} ×\ vecd {QR} &=\ begin {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\\ −8 e 6 e 2\\ −3 e 2\\ −3 e 2 e 0\ end {vmatrix}\\ [4pt]
&=0\ mathbf thbf {\ hat i} −6\ mathbf {\ hat j} −16\ mathbf {\ hat k} − (−18\ mathbf {\ hat k} +4\ mathbf {\ hat i} +0\ mathbf {\ hat j})\\ [4pt]
&=−4\ mathbf {\ hat i} −6\ mathbf {\ hat j} +2\ mathbf {\ hat k}. \ end {align*}\]

Vimos como usar o produto escalar triplo e como encontrar um vetor ortogonal a um plano. Agora, aplicamos o produto cruzado a situações do mundo real.

Às vezes, uma força faz com que um objeto gire. Por exemplo, girar uma chave de fenda ou uma chave inglesa cria esse tipo de efeito rotacional, chamado torque.

Definição: Torque

O torque\(\vecs \tau\) (a letra grega tau) mede a tendência de uma força produzir rotação em torno de um eixo de rotação. \(\vecs r\)Seja um vetor com um ponto inicial localizado no eixo de rotação e com um ponto terminal localizado no ponto onde a força é aplicada, e deixe o vetor\(\vecs F\) representar a força. Então o torque é igual ao produto cruzado de\(r\) e\(F\):

\[\vecs \tau=\vecs r×\vecs F. \nonumber \]

Veja a Figura\(\PageIndex{9}\).

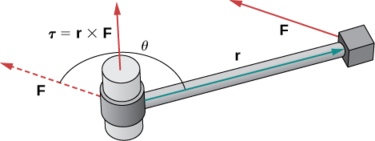
Esta figura tem um vetor r de um “eixo de rotação”. No ponto terminal de r há um vetor chamado “F”. O ângulo entre r e F é teta. — Figura\(\PageIndex{9}\): O torque mede como uma força faz com que um objeto gire.

Pense em usar uma chave inglesa para apertar um parafuso. O torque ω aplicado ao parafuso depende da força com que pressionamos a chave (força) e da distância da alça que aplicamos a força (distância). O torque aumenta com uma força maior na chave a uma distância maior do parafuso. As unidades comuns de torque são o newton-metro ou pé-libra. Embora o torque seja dimensionalmente equivalente ao trabalho (ele tem as mesmas unidades), os dois conceitos são distintos. O torque é usado especificamente no contexto de rotação, enquanto o trabalho normalmente envolve movimento ao longo de uma linha.

Exemplo\(\PageIndex{14}\): Evaluating Torque

Um parafuso é apertado aplicando uma força de\(6\) N a uma chave de 0,15 m (Figura\(\PageIndex{10}\)). O ângulo entre a chave e o vetor de força é\(40°\). Encontre a magnitude do torque em torno do centro do parafuso. Arredonde a resposta para duas casas decimais.

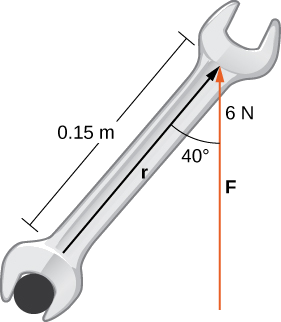
Esta figura é a imagem de uma chave aberta. O comprimento da chave é rotulado como “0,15 m”. O ângulo que a chave faz com um vetor vertical é de 40 graus. O vetor é rotulado com “6 N.” — Figura\(\PageIndex{10}\): O torque descreve a ação de torção da chave.

Solução:

Substitua as informações fornecidas na equação que define o torque:

\ [\ begin {align*} ‖\ vecs mt‖ &=\ |\ vecs r×\ vecs F\ |\\ [4pt]
&=‖\ vecs r\ vecs F\ sinθ\\ [4pt]
& =( 0,15\,\ texto {m}) (6\,\ texto {N})\ sin 40°\\ [4pt]
&≈ 0,58\,\ texto {N⋅m.} \ end {align*}\]

Exercício\(\PageIndex{14}\)

Calcule a força necessária para produzir torque de\(15\) N⋅m em um ângulo\(30º\) de uma haste de\(150\) -cm.

Dica: \(‖\vecs τ‖=15\)N⋅m e\(‖\vecs r‖=1.5\) m
Resposta: \(20\)N

Conceitos-chave

O produto cruzado\(\vecs u×\vecs v\) de dois vetores\(\vecs u=⟨u_1,u_2,u_3⟩\) e\(\vecs v=⟨v_1,v_2,v_3⟩\) é um vetor ortogonal a ambos\(\vecs u\)\(\vecs v\) e. Seu comprimento é dado por\(‖\vecs u×\vecs v‖=‖\vecs u‖⋅‖\vecs v‖⋅\sin θ,\) onde\(θ\) está o ângulo entre\(\vecs u\)\(\vecs v\) e. Sua direção é dada pela regra da mão direita.
A fórmula algébrica para calcular o produto cruzado de dois vetores,

\(\vecs u=⟨u_1,u_2,u_3⟩\)e\(\vecs v=⟨v_1,v_2,v_3⟩\), é

\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k}.\)

O produto cruzado satisfaz as seguintes propriedades para vetores\(\vecs u,\vecs v,\) e\(\vecs w\) e escalares\(c\):

\(\vecs u×\vecs v=−(\vecs v×\vecs u)\)

\(\vecs u×(\vecs v+\vecs w)=\vecs u×\vecs v+\vecs u×\vecs w\)

\(c(\vecs u×\vecs v)=(c\vecs u)×\vecs v=\vecs u×(c\vecs v)\)

\(\vecs u×\vecs 0=\vecs 0×\vecs u=\vecs 0\)

\(\vecs v×\vecs v=\vecs 0\)

\(\vecs u⋅(\vecs v×\vecs w)=(\vecs u×\vecs v)⋅\vecs w\)

O produto cruzado dos vetores\(\vecs u=⟨u_1,u_2,u_3⟩\) e\(\vecs v=⟨v_1,v_2,v_3⟩\) é o determinante\(\begin{vmatrix}\mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k}\\u_1 & u_2 & u_3\\v_1 & v_2 & v_3\end{vmatrix}\)
Se os\(\vecs u\) vetores\(\vecs v\) formarem lados adjacentes de um paralelogramo, a área do paralelogramo é dada por\(\|\vecs u×\vecs v\|.\)
O produto escalar triplo dos vetores\(\vecs u, \vecs v,\) e\(\vecs w\) é\(\vecs u⋅(\vecs v×\vecs w).\)
O volume de um paralelepípedo com bordas adjacentes dadas por vetores\(\vecs u,\vecs v\), e\(\vecs w\) é\(V=|\vecs u⋅(\vecs v×\vecs w)|.\)
Se o produto escalar triplo dos vetores\(\vecs u,\vecs v,\) e\(\vecs w\) for zero, então os vetores são coplanares. O inverso também é verdadeiro: se os vetores são coplanares, seu produto escalar triplo é zero.
O produto cruzado pode ser usado para identificar um vetor ortogonal a dois vetores determinados ou a um plano.
O torque\(\vecs τ\) mede a tendência de uma força produzir rotação em torno de um eixo de rotação. Se a força\(\vecs F\) estiver atuando a uma distância (deslocamento)\(\vecs r\) do eixo, então o torque é igual ao produto cruzado de\(\vecs r\) e\(\vecs F: \vecs τ=\vecs r×\vecs F.\)

Equações-chave

O produto cruzado de dois vetores em termos de vetores unitários

\[\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k} \nonumber \]

Glossário

produto cruzado

\(\vecs u×\vecs v=(u_2v_3−u_3v_2)\mathbf{\hat i}−(u_1v_3−u_3v_1)\mathbf{\hat j}+(u_1v_2−u_2v_1)\mathbf{\hat k},\)onde\(\vecs u=⟨u_1,u_2,u_3⟩\) e\(\vecs v=⟨v_1,v_2,v_3⟩\)

determinante

um número real associado a uma matriz quadrada

paralelepípedo

um prisma tridimensional com seis faces que são paralelogramos

torque

o efeito de uma força que faz com que um objeto gire

produto escalar triplo

o produto escalar de um vetor com o produto cruzado de dois outros vetores:\(\vecs u⋅(\vecs v×\vecs w)\)

produto vetorial

o produto cruzado de dois vetores