Skip to main content
Global

11.1: Equações paramétricas

  1. Last updated
  2. Save as PDF
  • Page ID
    187898

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de
    • Faça um gráfico de uma curva descrita por equações paramétricas.
    • Converta as equações paramétricas de uma curva na forma\(y=f(x)\).
    • Reconheça as equações paramétricas das curvas básicas, como uma linha e um círculo.
    • Reconheça as equações paramétricas de um ciclóide.

    Nesta seção, examinamos equações paramétricas e seus gráficos. No sistema de coordenadas bidimensional, as equações paramétricas são úteis para descrever curvas que não são necessariamente funções. O parâmetro é uma variável independente da qual\(y\) depende\(x\) e, à medida que o parâmetro aumenta, dos valores\(x\) e\(y\) traça um caminho ao longo de uma curva plana. Por exemplo, se o parâmetro for\(t\) (uma escolha comum), então\(t\) pode representar tempo. Em seguida,\(x\) e\(y\) são definidos como funções do tempo e\((x(t),y(t))\) podem descrever a posição no plano de um determinado objeto à medida que ele se move ao longo de um caminho curvo.

    Equações paramétricas e seus gráficos

    Considere a órbita da Terra ao redor do Sol. Nosso ano dura aproximadamente 365,25 dias, mas para essa discussão usaremos 365 dias. Em 1º de janeiro de cada ano, a localização física da Terra em relação ao Sol é quase a mesma, exceto nos anos bissextos, quando o atraso introduzido pelo\(\frac{1}{4}\) dia extra de tempo em órbita é incorporado ao calendário. Chamamos 1º de janeiro de “dia 1” do ano. Então, por exemplo, o dia 31 é 31 de janeiro, o dia 59 é 28 de fevereiro e assim por diante.

    O número do dia em um ano pode ser considerado uma variável que determina a posição da Terra em sua órbita. À medida que a Terra gira em torno do Sol, sua localização física muda em relação ao Sol. Depois de um ano inteiro, estamos de volta ao ponto de partida e um novo ano começa. De acordo com as leis do movimento planetário de Kepler, a forma da órbita é elíptica, com o Sol em um dos focos da elipse. Estudamos essa ideia com mais detalhes em Seções Cônicas.

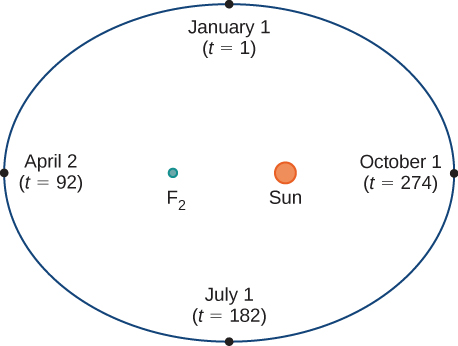
    Uma elipse com 1º de janeiro (t = 1) na parte superior, 2 de abril (t = 92) à esquerda, 1º de julho (t = 182) na parte inferior e 1º de outubro (t = 274) à direita. Os pontos focais da elipse têm F2 à esquerda e o Sol à direita.
    Figura\(\PageIndex{1}\): A órbita da Terra ao redor do Sol em um ano.

    A figura\( \PageIndex{1}\) mostra a órbita da Terra ao redor do Sol durante um ano. O ponto identificado\(F_2\) é um dos focos da elipse; o outro foco é ocupado pelo Sol. Se sobrepormos eixos de coordenadas sobre esse gráfico, poderemos atribuir pares ordenados a cada ponto na elipse (Figura\( \PageIndex{2}\)). Então, cada\(x\) valor no gráfico é um valor da posição em função do tempo, e cada\(y\) valor também é um valor da posição em função do tempo. Portanto, cada ponto no gráfico corresponde a um valor da posição da Terra em função do tempo.

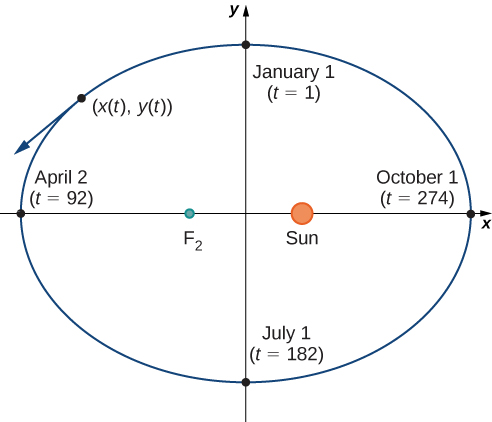
    Uma elipse com 1º de janeiro (t = 1) na parte superior, 2 de abril (t = 92) à esquerda, 1º de julho (t = 182) na parte inferior e 1º de outubro (t = 274) à direita. Os pontos focais da elipse têm F2 à esquerda e o Sol à direita. Há uma linha que vai de t = 1 a t = 182. Há também uma linha que vai de t = 92 a t = 274 que passa por F2 e o Sol. No lado superior esquerdo, há um ponto marcado (x (t), y (t)) com uma linha tangente apontando para baixo e para a esquerda.
    Figura\(\PageIndex{2}\): Eixos coordenados sobrepostos na órbita da Terra.

    Podemos determinar as funções\(x(t)\) e\(y(t)\), assim, parametrizar a órbita da Terra ao redor do Sol. A variável\(t\) é chamada de parâmetro independente e, nesse contexto, representa o tempo em relação ao início de cada ano.

    Uma curva no\((x,y)\) plano pode ser representada parametralmente. As equações usadas para definir a curva são chamadas de equações paramétricas.

    Definição: Equações paramétricas

    Se\(x\) e\(y\) são funções contínuas de\(t\) em um intervalo\(I\), então as equações

    \[x=x(t) \nonumber \]

    e

    \[y=y(t) \nonumber \]

    são chamadas de equações paramétricas e\(t\) são chamadas de parâmetro. O conjunto de pontos\((x,y)\) obtidos conforme\(t\) varia ao longo do intervalo\(I\) é chamado de gráfico das equações paramétricas. O gráfico das equações paramétricas é chamado de curva paramétrica ou curva plana e é indicado por\(C\).

    Observe nesta definição que\(x\) e\(y\) são usados de duas maneiras. A primeira é como funções da variável independente\(t\). Conforme\(t\) varia ao longo do intervalo\(I\), as funções\(x(t)\) e\(y(t)\) geram um conjunto de pares ordenados\((x,y)\). Esse conjunto de pares ordenados gera o gráfico das equações paramétricas. Neste segundo uso, para designar os pares ordenados,\(x\) e\(y\) são variáveis. É importante distinguir as variáveis\(x\) e\(y\) das funções\(x(t)\)\(y(t)\) e.

    Exemplo\(\PageIndex{1}\): Graphing a Parametrically Defined Curve

    Esboce as curvas descritas pelas seguintes equações paramétricas:

    1. \(x(t)=t−1, \quad y(t)=2t+4,\quad \text{for }−3≤t≤2\)
    2. \(x(t)=t^2−3, \quad y(t)=2t+1,\quad \text{for }−2≤t≤3\)
    3. \(x(t)=4 \cos t, \quad y(t)=4 \sin t,\quad \text{for }0≤t≤2π\)

    Solução

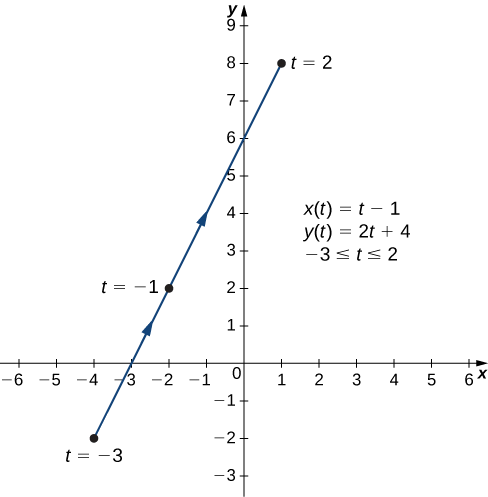
    a. Para criar um gráfico dessa curva, primeiro configure uma tabela de valores. Como a variável independente em ambos\(x(t)\) e\(y(t)\) é\(t\), vamos\(t\) aparecer na primeira coluna. Em seguida,\(x(t)\) e\(y(t)\) aparecerá na segunda e terceira colunas da tabela.

    \(t\) \(x(t)\) \(y(t)\)
    \ (t\)” style="alinhamento vertical: médio; ">−3 \ (x (t)\)” style="alinhamento vertical:médio; ">−4 \ (y (t)\)” style="alinhamento vertical: médio; ">−2
    \ (t\)” style="alinhamento vertical: médio; ">−2 \ (x (t)\)” style="alinhamento vertical: meio; ">−3 \ (y (t)\)” style="alinhamento vertical: médio; ">0
    \ (t\)” style="alinhamento vertical: médio; ">−1 \ (x (t)\)” style="alinhamento vertical:médio; ">−2 \ (y (t)\)” style="alinhamento vertical: médio; ">2
    \ (t\)” style="alinhamento vertical: médio; ">0 \ (x (t)\)” style="alinhamento vertical:médio; ">−1 \ (y (t)\)” style="alinhamento vertical: médio; ">4
    \ (t\)” style="alinhamento vertical: médio; ">1 \ (x (t)\)” style="alinhamento vertical: médio; ">0 \ (y (t)\)” style="alinhamento vertical: médio; ">6
    \ (t\)” style="alinhamento vertical: médio; ">2 \ (x (t)\)” style="alinhamento vertical: médio; ">1 \ (y (t)\)” style="alinhamento vertical: médio; ">8

    A segunda e a terceira colunas desta tabela fornecem um conjunto de pontos a serem plotados. O gráfico desses pontos aparece na Figura\( \PageIndex{3}\). As setas no gráfico indicam a orientação do gráfico, ou seja, a direção em que um ponto se move no gráfico quando t varia de −3 a 2.

    Uma linha reta indo de (−4, −2) até (−3, 0), (−2, 2) e (0, 6) até (1, 8) com a seta apontada para cima e para a direita. O ponto (−4, −2) é marcado com t = −3, o ponto (−2, 2) é marcado com t = −1 e o ponto (1, 8) está marcado com t = 2. No gráfico também estão escritas três equações: x (t) = t −1, y (t) = 2t + 4 e −3 ≤ t ≤ 2.
    Figura\(\PageIndex{3}\): Gráfico da curva plana descrita pelas equações paramétricas na parte a.

    b. Para criar um gráfico dessa curva, configure novamente uma tabela de valores.

    \(t\) \(x(t)\) \(y(t)\)
    \ (t\)” style="alinhamento vertical: médio; ">−2 \ (x (t)\)” style="alinhamento vertical: médio; ">1 \ (y (t)\)” style="alinhamento vertical: médio; ">−3
    \ (t\)” style="alinhamento vertical: médio; ">−1 \ (x (t)\)” style="alinhamento vertical:médio; ">−2 \ (y (t)\)” style="alinhamento vertical: médio; ">−1
    \ (t\)” style="alinhamento vertical: médio; ">0 \ (x (t)\)” style="alinhamento vertical: meio; ">−3 \ (y (t)\)” style="alinhamento vertical: médio; ">1
    \ (t\)” style="alinhamento vertical: médio; ">1 \ (x (t)\)” style="alinhamento vertical:médio; ">−2 \ (y (t)\)” style="alinhamento vertical: médio; ">3
    \ (t\)” style="alinhamento vertical: médio; ">2 \ (x (t)\)” style="alinhamento vertical: médio; ">1 \ (y (t)\)” style="alinhamento vertical: médio; ">5
    \ (t\)” style="alinhamento vertical: médio; ">3 \ (x (t)\)” style="alinhamento vertical: médio; ">6 \ (y (t)\)” style="alinhamento vertical: médio; ">7

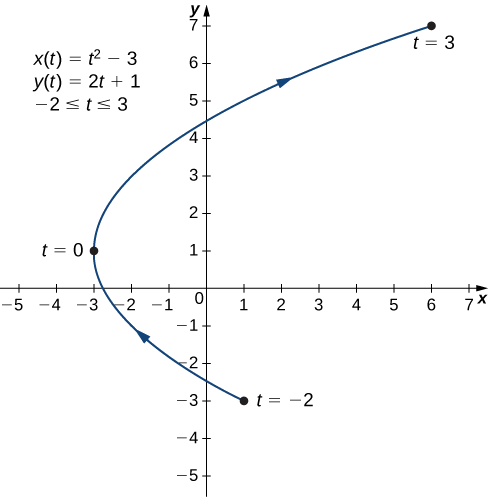
    A segunda e a terceira colunas desta tabela fornecem um conjunto de pontos a serem plotados (Figura\( \PageIndex{4}\)). O primeiro ponto no gráfico (correspondente a\(t=−2\)) tem coordenadas\((1,−3)\) e o último ponto (correspondente a\(t=3\)) tem coordenadas\((6,7)\). À medida que\(t\) avança de\(−2\) para\(3\), o ponto na curva viaja ao longo de uma parábola. A direção em que o ponto se move é novamente chamada de orientação e é indicada no gráfico.

    Uma linha curva que vai de (1, −3) até (−3, 1) até (6, 7) com a seta apontando nessa ordem. O ponto (1, −3) está marcado com t = −2, o ponto (−3, 1) está marcado com t = 0 e o ponto (6, 7) está marcado com t = 3. No gráfico também estão escritas três equações: x (t) = t2 − 3, y (t) = 2t + 1 e −2 ≤ t ≤ 3.
    Figura\(\PageIndex{4}\): Gráfico da curva plana descrita pelas equações paramétricas na parte b.

    c. Nesse caso, use múltiplos de\(π/6\) for\(t\) e crie outra tabela de valores:

    \(t\) \(x(t)\) \(y(t)\) \(t\) \(x(t)\) \(y(t)\)
    \ (t\)” style="alinhamento vertical: médio; ">0 \ (x (t)\)” style="alinhamento vertical: médio; ">4 \ (y (t)\)” style="alinhamento vertical: médio; ">0 \ (t\)” style="alinhamento vertical: médio; ">\(\frac{7π}{6}\) \ (x (t)\)” style="alinhamento vertical: meio; ">\(-2\sqrt{3}≈−3.5\) \ (y (t)\)” style="alinhamento vertical: médio; ">-2
    \ (t\)” style="alinhamento vertical: médio; ">\(\frac{π}{6}\) \ (x (t)\)” style="alinhamento vertical: meio; ">\(2\sqrt{3}≈3.5\) \ (y (t)\)” style="alinhamento vertical: médio; ">2 \ (t\)” style="alinhamento vertical: médio; ">\(\frac{4π}{3}\) \ (x (t)\)” style="alinhamento vertical:médio; ">−2 \ (y (t)\)” style="alinhamento vertical: meio; ">\(−2\sqrt{3}≈−3.5\)
    \ (t\)” style="alinhamento vertical: médio; ">\(\frac{π}{3}\) \ (x (t)\)” style="alinhamento vertical: médio; ">2 \ (y (t)\)” style="alinhamento vertical: meio; ">\(2\sqrt{3}≈3.5\) \ (t\)” style="alinhamento vertical: médio; ">\(\frac{3π}{2}\) \ (x (t)\)” style="alinhamento vertical: médio; ">0 \ (y (t)\)” style="alinhamento vertical: médio; ">−4
    \ (t\)” style="alinhamento vertical: médio; ">\(\frac{π}{2}\) \ (x (t)\)” style="alinhamento vertical: médio; ">0 \ (y (t)\)” style="alinhamento vertical: médio; ">4 \ (t\)” style="alinhamento vertical: médio; ">\(\frac{5π}{3}\) \ (x (t)\)” style="alinhamento vertical: médio; ">2 \ (y (t)\)” style="alinhamento vertical: meio; ">\(−2\sqrt{3}≈−3.5\)
    \ (t\)” style="alinhamento vertical: médio; ">\(\frac{2π}{3}\) \ (x (t)\)” style="alinhamento vertical:médio; ">−2 \ (y (t)\)” style="alinhamento vertical: meio; ">\(2\sqrt{3}≈3.5\) \ (t\)” style="alinhamento vertical: médio; ">\(\frac{11π}{6}\) \ (x (t)\)” style="alinhamento vertical: meio; ">\(2\sqrt{3}≈3.5\) \ (y (t)\)” style="alinhamento vertical: médio; ">-2
    \ (t\)” style="alinhamento vertical: médio; ">\(\frac{5π}{6}\) \ (x (t)\)” style="alinhamento vertical: meio; ">\(−2\sqrt{3}≈−3.5\) \ (y (t)\)” style="alinhamento vertical: médio; ">2 \ (t\)” style="alinhamento vertical: médio; ">\(2π\) \ (x (t)\)” style="alinhamento vertical: médio; ">4 \ (y (t)\)” style="alinhamento vertical: médio; ">0
    \ (t\)” style="alinhamento vertical: médio; ">\(π\) \ (x (t)\)” style="alinhamento vertical:médio; ">−4 \ (y (t)\)” style="alinhamento vertical: médio; ">0 \ (t\)” style="alinhamento vertical: médio; "> \ (x (t)\)” style="alinhamento vertical: meio; "> \ (y (t)\)” style="alinhamento vertical: meio; ">

    O gráfico dessa curva plana aparece no gráfico a seguir.

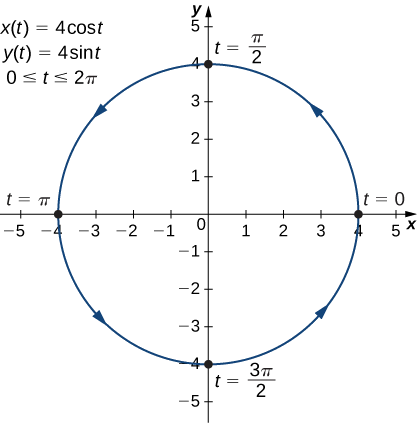
    Um círculo com raio 4 centrado na origem é representado graficamente com uma seta no sentido anti-horário. O ponto (4, 0) está marcado com t = 0, o ponto (0, 4) está marcado com t = π /2, o ponto (−4, 0) está marcado com t = π e o ponto (0, −4) está marcado com t = 3π /2. No gráfico também estão escritas três equações: x (t) = 4 cos (t), y (t) = 4 sin (t) e 0 ≤ t ≤ 2π.
    Figura\(\PageIndex{5}\): Gráfico da curva plana descrita pelas equações paramétricas na parte c.

    Este é o gráfico de um círculo com raio\(4\) centrado na origem, com orientação anti-horária. O ponto inicial e o ponto final da curva têm coordenadas\((4,0)\).

    Exercício\(\PageIndex{1}\)

    Esboce a curva descrita pelas equações paramétricas

    \[ x(t)=3t+2,\quad y(t)=t^2−1,\quad \text{for }−3≤t≤2. \nonumber \]

    Dica

    Faça uma tabela de valores para\(x(t)\) e\(y(t)\) usando\(t\) valores de\(−3\) até\(2\).

    Resposta

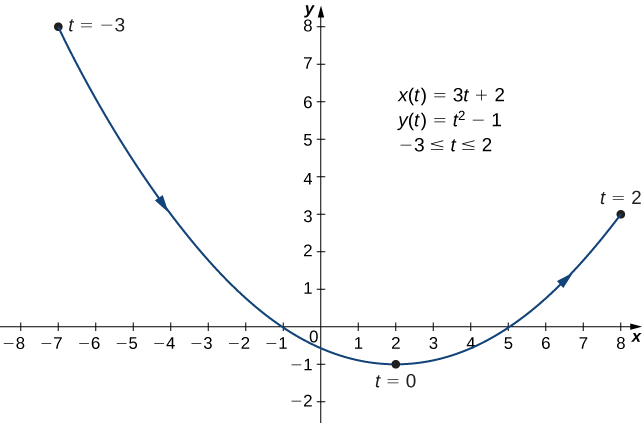
    Uma linha curva indo de (−7, 8) até (−1, 0) e (2, −1) até (8, 3) com a seta indo nessa ordem. O ponto (−7, 8) está marcado com t = −3, o ponto (2, −1) está marcado com t = 0 e o ponto (8, 3) está marcado com t = 2. No gráfico também estão escritas três equações: x (t) = 3t + 2, y (t) = t2 − 1 e −3 ≤ t ≤ 2.

    Eliminando o parâmetro

    Para entender melhor o gráfico de uma curva representada parametralmente, é útil reescrever as duas equações como uma única equação relacionando as variáveis\(x\)\(y\) e. Em seguida, podemos aplicar qualquer conhecimento prévio de equações de curvas no plano para identificar a curva. Por exemplo, as equações que descrevem a curva plana em Exemplo\(\PageIndex{1b}\) são

    \[\begin{align} x(t) &=t^2−3 \label{x1} \\[4pt] y(t) &=2t+1 \label{y1} \end{align} \]

    sobre a região\(-2 \le t \le 3.\)

    Resolvendo a equação\ ref {y1} para\(t\) dados

    \[t=\dfrac{y−1}{2}. \nonumber \]

    Isso pode ser substituído na Equação\ ref {x1}:

    \[\begin{align} x &=\left(\dfrac{y−1}{2}\right)^2−3 \\[4pt] &=\dfrac{y^2−2y+1}{4}−3 \\[4pt] &=\dfrac{y^2−2y−11}{4}. \label{y2}\end{align} \]

    A equação\ ref {y2} é\(x\) descrita como uma função de\(y\). Essas etapas fornecem um exemplo de eliminação do parâmetro. O gráfico dessa função é uma parábola que se abre à direita (Figura\(\PageIndex{4}\)). Lembre-se de que a curva plana começou em\((1,−3)\) e terminou em\((6,7)\). Essas terminações ocorreram devido à restrição do parâmetro\(t\).

    Exemplo\(\PageIndex{2}\): Eliminating the Parameter

    Elimine o parâmetro para cada uma das curvas planas descritas pelas seguintes equações paramétricas e descreva o gráfico resultante.

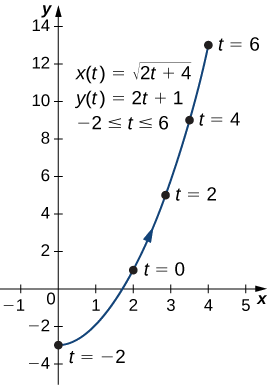
    1. \(x(t)=\sqrt{2t+4}, \quad y(t)=2t+1,\quad \text{for }−2≤t≤6\)
    2. \(x(t)=4\cos t, \quad y(t)=3\sin t,\quad \text{for }0≤t≤2π\)

    Solução

    a. Para eliminar o parâmetro, podemos resolver qualquer uma das equações para\(t\). Por exemplo, resolvendo a primeira equação para\(t\) dá

    \[\begin{align*} x &=\sqrt{2t+4} \\[4pt] x^2 &=2t+4 \\[4pt] x^2−4 &=2t \\[4pt] t &=\dfrac{x^2−4}{2}. \end{align*}\]

    Observe que quando quadramos os dois lados, é importante observar isso\(x≥0\). Substituindo\(t=\dfrac{x^2−4}{2}\) em\(y(t)\) rendimentos

    \[ y(t)=2t+1 \nonumber \]

    \[ y=2\left(\dfrac{x^2−4}{2}\right)+1 \nonumber \]

    \[ y=x^2−4+1 \nonumber \]

    \[ y=x^2−3. \nonumber \]

    Essa é a equação de uma parábola se abrindo para cima. No entanto, há uma restrição de domínio devido aos limites do parâmetro\(t\). Quando\(t=−2\)\(x=\sqrt{2(−2)+4}=0\), e quando\(t=6\),\(x=\sqrt{2(6)+4}=4\). O gráfico dessa curva plana segue.

    Uma linha curva indo de (−3, 0) até (2, 1) até (4, 13) com a seta indo nessa ordem. O ponto (−3, 0) está marcado com t = −2, o ponto (2, 1) está marcado com t = 0, o ponto (2 vezes a raiz quadrada de 2, 5) está marcado com t = 2, o ponto (3 vezes a raiz quadrada de 2, 9) está marcado com t = 4 e o ponto (4, 13) está marcado com t = 6. No gráfico também estão escritas três equações: x (t) = raiz quadrada da quantidade (2t + 4), y (t) = 2t + 1 e −2 ≤ t ≤ 6.
    Figura\(\PageIndex{6}\): Gráfico da curva plana descrita pelas equações paramétricas na parte a.

    b. Às vezes, é necessário ser um pouco criativo ao eliminar o parâmetro. As equações paramétricas para este exemplo são

    \[ x(t)=4 \cos t\nonumber \]

    e

    \[ y(t)=3 \sin t\nonumber \]

    Resolver qualquer uma das equações\(t\) diretamente não é aconselhável porque seno e cosseno não são funções individuais. No entanto, dividir a primeira equação por\(4\) e a segunda equação por\(3\) (e suprimir a\(t\)) nos dá

    \[ \cos t=\dfrac{x}{4}\nonumber \]

    e

    \[ \sin t=\dfrac{y}{3}.\nonumber \]

    Agora use a identidade pitagórica\(\cos^2t+\sin^2t=1\) e substitua as expressões para\(\sin t\) e\(\cos t\) pelas expressões equivalentes em termos de\(x\)\(y\) e. Isso dá

    \[ \left(\dfrac{x}{4}\right)^2+\left(\dfrac{y}{3}\right)^2=1 \nonumber \]

    \[ \dfrac{x^2}{16}+\dfrac{y^2}{9}=1. \nonumber \]

    Esta é a equação de uma elipse horizontal centrada na origem, com semi-eixo maior\(4\) e semi-eixo menor,\(3\) conforme mostrado no gráfico a seguir.

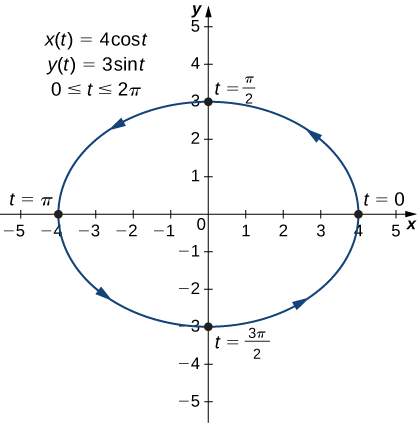
    Uma elipse com eixo maior horizontal e de comprimento 8 e com raio menor vertical e comprimento 6 que está centrada na origem com a seta indo no sentido anti-horário. O ponto (4, 0) está marcado com t = 0, o ponto (0, 3) está marcado com t = π /2, o ponto (−4, 0) está marcado com t = π e o ponto (0, −3) está marcado com t = 3π /2. No gráfico também estão escritas três equações: x (t) = 4 cos (t), y (t) = 3 sin (t) e 0 ≤ t ≤ 2π.
    Figura\(\PageIndex{7}\): Gráfico da curva plana descrita pelas equações paramétricas na parte b.

    Conforme t avança de\(0\) para\(2π\), um ponto na curva atravessa a elipse uma vez, no sentido anti-horário. Lembre-se, na abertura da seção, de que a órbita da Terra ao redor do Sol também é elíptica. Esse é um exemplo perfeito do uso de curvas parametrizadas para modelar um fenômeno do mundo real.

    Exercício\(\PageIndex{2}\)

    Elimine o parâmetro da curva plana definida pelas seguintes equações paramétricas e descreva o gráfico resultante.

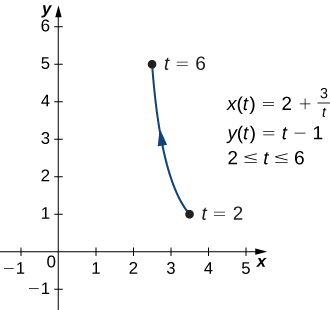
    \[ x(t)=2+\dfrac{3}{t}, \quad y(t)=t−1, \quad\text{for }2≤t≤6 \nonumber \]

    Dica

    Resolva uma das equações\(t\) e substitua-a pela outra equação.

    Resposta

    \(x=2+\frac{3}{y+1},\)ou\(y=−1+\frac{3}{x−2}\). Esta equação descreve uma parte de uma hipérbole retangular centrada em\((2,−1)\).

    Uma linha curva indo de (3,5, 1) a (2,5, 5) com a seta indo nessa ordem. O ponto (3,5, 1) está marcado com t = 2 e o ponto (2,5, 5) está marcado com t = 6. No gráfico também estão escritas três equações: x (t) = 2 + 3/t, y (t) = t − 1 e 2 ≤ t ≤ 6.

    Até agora, vimos o método de eliminar o parâmetro, assumindo que conhecemos um conjunto de equações paramétricas que descrevem uma curva plana. E se quisermos começar com a equação de uma curva e determinar um par de equações paramétricas para essa curva? Isso certamente é possível e, de fato, é possível fazer isso de muitas maneiras diferentes para uma determinada curva. O processo é conhecido como parametrização de uma curva.

    Exemplo\(\PageIndex{3}\): Parameterizing a Curve

    Encontre dois pares diferentes de equações paramétricas para representar o gráfico de\(y=2x^2−3\).

    Solução

    Primeiro, sempre é possível parametrizar uma curva definindo e\(x(t)=t\), em seguida,\(x\) substituindo por\(t\) na equação para\(y(t)\). Isso fornece a parametrização

    \[ x(t)=t, \quad y(t)=2t^2−3. \nonumber \]

    Como não há restrição ao domínio no gráfico original, não há restrição nos valores de\(t\).

    Temos total liberdade na escolha da segunda parametrização. Por exemplo, podemos escolher\(x(t)=3t−2\). A única coisa que precisamos verificar é se não há restrições impostas\(x\); ou seja, o intervalo de\(x(t)\) são todos números reais. Esse é o caso de\(x(t)=3t−2\). Agora\(y=2x^2−3\), desde então, podemos substituir\(x(t)=3t−2\) por\(x\). Isso dá

    \[ y(t)=2(3t−2)^2−2=2(9t^2−12t+4)−2=18t^2−24t+8−2=18t^2−24t+6. \nonumber \]

    Portanto, uma segunda parametrização da curva pode ser escrita como

    \( x(t)=3t−2\)e\( y(t)=18t^2−24t+6.\)

    Exercício\(\PageIndex{3}\)

    Encontre dois conjuntos diferentes de equações paramétricas para representar o gráfico de\(y=x^2+2x\).

    Dica

    Siga as etapas em Exemplo\(\PageIndex{3}\). Lembre-se de que temos liberdade para escolher a parametrização para\(x(t)\).

    Resposta

    Uma possibilidade é\(x(t)=t, \quad y(t)=t^2+2t.\) Outra possibilidade é\(x(t)=2t−3, \quad y(t)=(2t−3)^2+2(2t−3)=4t^2−8t+3.\) Existem, de fato, um número infinito de possibilidades.

    Cicloides e outras curvas paramétricas

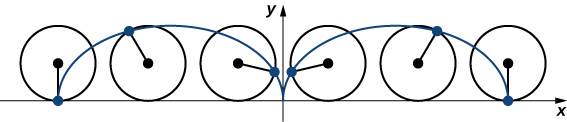
    Imagine fazer um passeio de bicicleta pelo país. Os pneus permanecem em contato com a estrada e giram em um padrão previsível. Agora, suponha que uma formiga muito determinada esteja cansada depois de um longo dia e queira voltar para casa. Então ele fica pendurado na lateral do pneu e ganha uma carona grátis. O caminho que essa formiga percorre por uma estrada reta é chamado de ciclóide (Figura\( \PageIndex{8}\)). Um ciclóide gerado por um círculo (ou roda de bicicleta) de raio a é dado pelas equações paramétricas

    \[x(t)=a(t−\sin t), \quad y(t)=a(1−\cos t).\nonumber \]

    Para ver por que isso é verdade, considere o caminho que o centro da roda percorre. O centro se move ao longo do\(x\) eixo -a uma altura constante igual ao raio da roda. Se o raio for\(a\), então as coordenadas do centro podem ser dadas pelas equações

    \[x(t)=at,\quad y(t)=a\nonumber \]

    para qualquer valor de\(t\). Em seguida, considere a formiga, que gira em torno do centro ao longo de um caminho circular. Se a bicicleta estiver se movendo da esquerda para a direita, as rodas girarão no sentido horário. Uma possível parametrização do movimento circular da formiga (em relação ao centro da roda) é dada por

    \[\begin{align*} x(t) &=−a \sin t \\[4pt] y(t) &=−a\cos t.\end{align*}\]

    (O sinal negativo é necessário para inverter a orientação da curva. Se o sinal negativo não estivesse lá, teríamos que imaginar a roda girando no sentido anti-horário.) A soma dessas equações fornece as equações para o ciclóide.

    \[\begin{align*} x(t) &=a(t−\sin t) \\[4pt] y(t) &=a(1−\cos t ) \end{align*}\]

    Uma série de círculos com o centro marcado e um ponto no círculo desenhando uma curva como se o círculo estivesse rolando ao longo de um plano. A forma feita parece ser meia elipse com altura do diâmetro do círculo original e com eixo maior a circunferência do círculo.
    Figura\(\PageIndex{8}\): Uma roda viajando por uma estrada sem escorregar; a ponta na borda da roda traça um ciclóide.

    Agora, suponha que a roda da bicicleta não viaje por uma estrada reta, mas se mova pela parte interna de uma roda maior, como na Figura\( \PageIndex{9}\). Neste gráfico, o círculo verde está viajando ao redor do círculo azul no sentido anti-horário. Um ponto na borda do círculo verde traça o gráfico vermelho, que é chamado de hipociclóide.

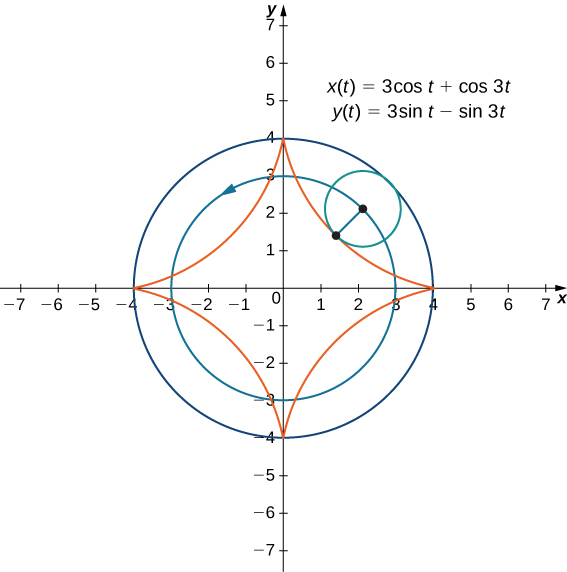
    Dois círculos são desenhados com o centro na origem e com os raios 3 e 4, respectivamente; o círculo com raio 3 tem uma seta apontando no sentido anti-horário. Há um terceiro círculo desenhado com centro no círculo com raio 3 e tocando o círculo com raio 4 em um ponto. Ou seja, esse terceiro círculo tem raio 1. Um ponto é desenhado nesse terceiro círculo e, se rolasse ao longo dos outros dois círculos, desenharia uma estrela de quatro pontas com pontos em (4, 0), (0, 4), (−4, 0) e (0, −4). No gráfico também estão escritas duas equações: x (t) = 3 cos (t) + cos (3t) e y (t) = 3 sin (t) — sin (3t).
    Figura\(\PageIndex{9}\): Gráfico do hipociclóide descrito pelas equações paramétricas mostradas.

    As equações paramétricas gerais para um hipociclóide são

    \[x(t)=(a−b) \cos t+b \cos (\dfrac{a−b}{b})t \nonumber \]

    \[y(t)=(a−b) \sin t−b \sin (\dfrac{a−b}{b})t. \nonumber \]

    Essas equações são um pouco mais complicadas, mas a derivação é um pouco semelhante às equações do ciclóide. Nesse caso, assumimos que o raio do círculo maior é\(a\) e o raio do círculo menor é\(b\). Em seguida, o centro da roda viaja ao longo de um círculo de raio.\(a−b.\) Esse fato explica o primeiro termo em cada equação acima. O período da segunda função trigonométrica em ambas\(x(t)\) e\(y(t)\) é igual\(\dfrac{2πb}{a−b}\) a.

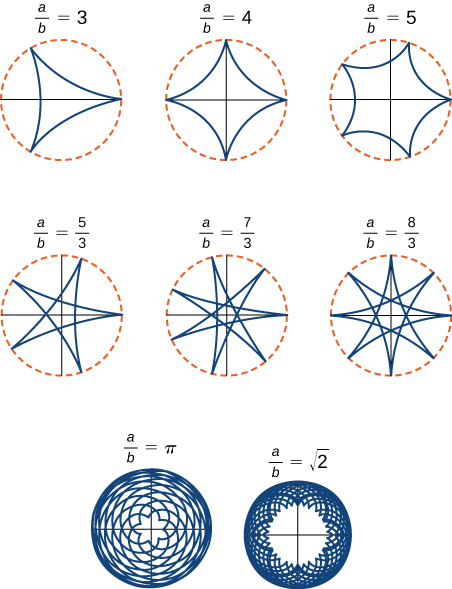
    A proporção\(\dfrac{a}{b}\) está relacionada ao número de cúspides no gráfico (as cúspides são os cantos ou extremidades pontiagudas do gráfico), conforme ilustrado na Figura\( \PageIndex{10}\). Essa proporção pode levar a alguns gráficos muito interessantes, dependendo se a proporção é racional ou não. A figura\(\PageIndex{9}\) corresponde a\(a=4\)\(b=1\) e. O resultado é um hipociclóide com quatro cúspides. A figura\(\PageIndex{10}\) mostra algumas outras possibilidades. Os dois últimos hipociclóides têm valores irracionais para\(\dfrac{a}{b}\). Nesses casos, os hipociclóides têm um número infinito de cúspides, então eles nunca retornam ao ponto de partida. Esses são exemplos do que é conhecido como curvas de preenchimento de espaço.

    Uma série de hipociclóides é fornecida. A primeira é uma estrela de três pontas marcada com a/b = 3. A segunda é uma estrela de quatro pontas marcada com a/b = 4. A terceira é uma estrela de cinco pontas marcada com a/b = 5. Nenhuma dessas três primeiras figuras tem linhas que se cruzam. A quarta figura é uma estrela de cinco pontas, mas esta tem linhas que se cruzam e se parece com a estrela que as crianças aprendem a desenhar pela primeira vez; está marcada com a/b = 5/3. Um tipo similar de estrela com sete pontos é o próximo e está marcado com a/b = 7/3. Então, uma estrela similar com oito pontos é a próxima e é marcada com a/b = 8/3. A figura a seguir é uma série complicada de curvas que, em última análise, cria uma pequena roseta no meio; ela está marcada com a/b = π. Por fim, há uma série de curvas ainda mais complicada que cria uma grande roseta com floretes mais nítidos marcados com a/b = a raiz quadrada de 2.
    Figura\(\PageIndex{10}\): Gráfico de vários hipociclóides correspondentes a diferentes valores de\(a/b\).
    A Bruxa de Agnesi

    Muitas curvas planas em matemática têm o nome das pessoas que as investigaram pela primeira vez, como o folium de Descartes ou a espiral de Arquimedes. No entanto, talvez o nome mais estranho para uma curva seja a bruxa de Agnesi. Por que uma bruxa?

    Maria Gaetana Agnesi (1718—1799) foi uma das poucas mulheres matemáticas reconhecidas da Itália do século XVIII. Ela escreveu um livro popular sobre geometria analítica, publicado em 1748, que incluía uma curva interessante que havia sido estudada por Fermat em 1630. O matemático Guido Grandi mostrou em 1703 como construir essa curva, que mais tarde chamou de “versoria”, um termo latino para uma corda usada na navegação. Agnesi usou o termo italiano para essa corda, “versiera”, mas em latim, essa mesma palavra significa “duende fêmea”. Quando o livro de Agnesi foi traduzido para o inglês em 1801, o tradutor usou o termo “bruxa” para a curva, em vez de corda. O nome “bruxa de Agnesi” permanece desde então.

    A bruxa de Agnesi é uma curva definida da seguinte forma: Comece com um círculo de raio a para que os pontos\((0,0)\) e\((0,2a)\) sejam pontos no círculo (Figura\( \PageIndex{11}\)). Deixe O indicar a origem. Escolha qualquer outro ponto A no círculo e desenhe a linha secante OA. Seja B denotar o ponto em que a linha OA cruza a linha horizontal\((0,2a)\). A linha vertical que passa por B cruza a linha horizontal através de A no ponto P. À medida que o ponto A varia, o caminho que o ponto P percorre é a bruxa da curva de Agnesi para o círculo dado.

    As curvas de Witch of Agnesi têm aplicações em física, incluindo modelagem de ondas de água e distribuições de linhas espectrais. Na teoria da probabilidade, a curva descreve a função de densidade de probabilidade da distribuição de Cauchy. Neste projeto, você parametrizará essas curvas.

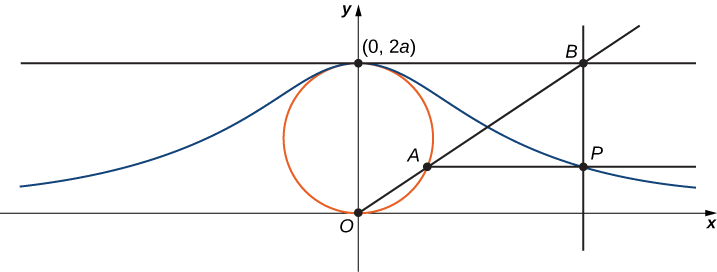
    Um círculo com a parte inferior no ponto O (a origem) e a parte superior no ponto (0, 2a) é desenhado. O eixo x é desenhado do ponto O e o eixo y é traçado do ponto O até (0, 2a). Paralela ao eixo x está uma linha desenhada a partir de (0, 2a); ela tem o ponto B marcado à direita. Uma linha do ponto B ao ponto O passa pelo círculo no ponto A. Uma linha é desenhada paralelamente ao eixo x a partir do ponto A e forma um ângulo reto com uma linha traçada abaixo do ponto B; essas linhas se cruzam no ponto P. Há uma curva que é simétrica em relação ao eixo y que passa pelo ponto P. a curva tem seu máximo em (0, 2a) e diminui suavemente através do ponto P.
    Figura\(\PageIndex{11}\): Conforme o ponto\(A\) se move ao redor do círculo, o ponto\(P\) traça a curva da bruxa de Agnesi para o círculo dado.

    1. Na figura, identifique os seguintes pontos, comprimentos e ângulos:

    a.\(C\) é o ponto no\(x\) eixo -com a mesma\(x\) coordenada -de\(A\).

    b.\(x\) é a\(x\) coordenada -de\(P\) e\(y\) é a\(y\) coordenada -de\(P\).

    c.\(E\) é o ponto\((0,a)\).

    d.\(F\) é o ponto no segmento de linha de\(OA\) forma que o segmento de linha\(EF\) seja perpendicular ao segmento de linha\(OA\).

    e.\(b\) é a distância\(O\) de\(F\) a.

    f.\(c\) é a distância\(F\) de\(A\) a.

    g.\(d\) é a distância\(O\) de\(C\) a.

    h.\(θ\) é a medida do ângulo\(∠COA\).

    O objetivo deste projeto é parametrizar a bruxa usando\(θ\) como parâmetro. Para fazer isso, escreva equações para\(x\) e\(y\) em termos de apenas\(θ\).

    2. Mostre isso\(d=\dfrac{2a}{\sin θ}\).

    3. Observe isso\(x=d\cos θ\). Mostre isso\(x=2a\cot θ\). Ao fazer isso, você terá parametrizado a\(x\) coordenada -da curva em relação\(θ\) a. Se você conseguir obter uma equação semelhante para\(y\), você terá parametrizado a curva.

    4. Em termos de\(θ\), qual é o ângulo\(∠EOA\)?

    5. Mostre isso\(b+c=2a\cos\left(\frac{π}{2}−θ\right)\).

    6. Mostre isso\(y=2a\cos\left(\frac{π}{2}−θ\right)\sin θ\).

    7. Mostre isso\(y=2a\sin^2θ\). Agora você parametrizou a\(y\) coordenada -da curva em relação\(θ\) a.

    8. Conclua que uma parametrização da curva de bruxa dada é

    \[x=2a\cot θ, \quad y=2a \sin^2θ, \quad\text{for }−∞<θ<∞. \nonumber \]

    9. Use sua parametrização para mostrar que a curva de bruxa dada é o gráfico da função\(f(x)=\dfrac{8a^3}{x^2+4a^2}\).

    Viaja com minha formiga: os cicloides de curtato e prolato

    No início desta seção, examinamos as equações paramétricas de um ciclóide, que é o caminho que um ponto na borda de uma roda traça enquanto a roda rola ao longo de um caminho reto. Neste projeto, examinamos duas variações diferentes do ciclóide, chamadas cicloides curtato e prolato.

    Primeiro, vamos revisitar a derivação das equações paramétricas de um ciclóide. Lembre-se de que consideramos uma formiga tenaz tentando chegar em casa pendurada na ponta de um pneu de bicicleta. Presumimos que a formiga subiu no pneu bem na ponta, onde o pneu toca o chão. Enquanto a roda gira, a formiga se move com a ponta do pneu (Figura\(\PageIndex{12}\)).

    Como discutimos, temos muita flexibilidade ao parametrizar uma curva. Nesse caso, deixamos nosso parâmetro t representar o ângulo pelo qual o pneu girou. Olhando para a Figura\( \PageIndex{12}\), vemos que depois que o pneu gira em um ângulo de\(t\), a posição do centro da roda,\(C=(x_C,y_C)\), é dada por

    \(x_C=at\)\(y_C=a\)e.

    Além disso, deixando\(A=(x_A,y_A)\) indicar a posição da formiga, notamos que

    \(x_C−x_A=a\sin t\)e\(y_C−y_A=a \cos t\)

    Então

    \[x_A=x_C−a\sin t=at−a\sin t=a(t−\sin t) \nonumber \]

    \[y_A=y_C−a\cos t=a−a\cos t=a(1−\cos t). \nonumber \]

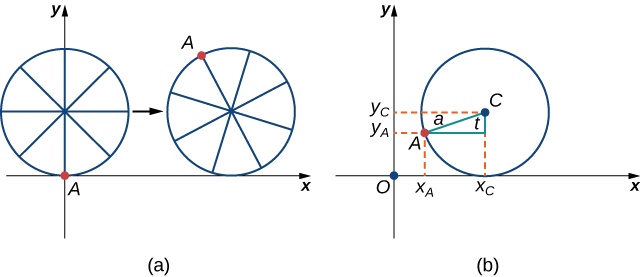
    Existem duas figuras marcadas (a) e (b). A figura a tem um círculo com o ponto A no círculo na origem. O círculo tem “raios”, com o ponto A no final de um desses raios. O círculo parece estar viajando para a direita no eixo x, com o ponto A acima do eixo x em uma segunda imagem do círculo desenhado ligeiramente à direita. A Figura b tem um círculo no primeiro quadrante com o centro C. Ela toca o eixo x em xc. Um ponto A é desenhado no círculo e um triângulo reto é formado a partir desse ponto e do ponto C. A hipotenusa é marcada como a e o ângulo em C entre A e xc é marcado com t. As linhas são desenhadas para fornecer os valores x e y de A como xA e yA, respectivamente. Da mesma forma, uma linha é desenhada para fornecer o valor y de C como yC.
    Figura\(\PageIndex{12}\): (a) A formiga se agarra à borda do pneu da bicicleta enquanto o pneu rola pelo chão. (b) Usando a geometria para determinar a posição da formiga após o pneu ter girado em um ângulo de\(t\).

    Observe que essas são as mesmas representações paramétricas que tínhamos antes, mas agora atribuímos um significado físico à variável paramétrica\(t\).

    Depois de um tempo, a formiga fica tonta ao dar voltas e voltas na ponta do pneu. Então ele sobe por um dos raios em direção ao centro da roda. Ao subir em direção ao centro da roda, a formiga mudou seu caminho de movimento. O novo caminho tem menos movimento para cima e para baixo e é chamado de ciclóide curtado (Figura\( \PageIndex{13}\)). Conforme mostrado na figura, deixamos b indicar a distância ao longo do raio do centro da roda até a formiga. Como antes, deixamos t representar o ângulo pelo qual o pneu girou. Além disso, deixamos\(C=(x_C,y_C)\) representar a posição do centro da roda e\(A=(x_A,y_A)\) representar a posição da formiga.

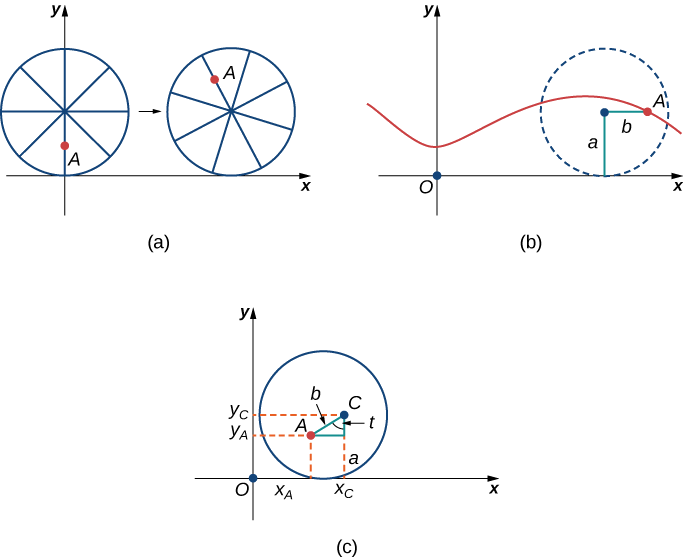
    Há três figuras marcadas (a), (b) e (c). A figura a tem um círculo com “raios”, onde o ponto A está no meio de um desses raios. O círculo é tangente ao eixo x na origem. O círculo parece estar viajando para a direita no eixo x, com o ponto A mais acima em uma segunda imagem do círculo desenhado ligeiramente à direita. A Figura b mostra a curva que o ponto A traçaria, à medida que o círculo viaja para a direita. É vagamente sinusoidal. A figura c tem um círculo no primeiro quadrante com o centro C. Ela toca o eixo x em xc. Um ponto A é desenhado dentro do círculo e um triângulo reto é formado a partir desse ponto e do ponto C. A hipotenusa é marcada com b, o ângulo em C entre A e xc é marcado como t e a distância de C a xc é marcada como a. As linhas são desenhadas para fornecer os valores x e y de A como xA e yA, respectivamente. Da mesma forma, uma linha é desenhada para fornecer o valor y de C como yC.
    Figura\(\PageIndex{13}\): (a) A formiga sobe por um dos raios em direção ao centro da roda. (b) O caminho de movimento da formiga depois que ela se aproxima do centro da roda. Isso é chamado de ciclóide curtate. (c) A nova configuração, agora que a formiga se aproximou do centro da roda.

    1. Qual é a posição do centro da roda após o pneu ter girado em um ângulo de\(t\)?

    2. Use a geometria para encontrar expressões para\(x_C−x_A\) e para\(y_C−y_A\).

    3. Com base em suas respostas às partes 1 e 2, quais são as equações paramétricas que representam o ciclóide curtate?

    Quando a cabeça da formiga clareia, ele percebe que o ciclista fez uma curva e agora está viajando para longe de sua casa. Então ele deixa cair o pneu da bicicleta e olha em volta. Felizmente, há um conjunto de trilhos de trem nas proximidades, voltando na direção certa. Então, a formiga vai até os trilhos do trem para esperar. Depois de um tempo, um trem passa, indo na direção certa, e ele consegue pular e simplesmente pegar a ponta da roda do trem (sem ser esmagado!).

    A formiga ainda está preocupada em ficar tonta, mas a roda do trem está escorregadia e não tem raios para subir, então ela decide ficar na ponta do volante e torcer pelo melhor. Agora, as rodas do trem têm uma flange para manter a roda funcionando nos trilhos. Portanto, nesse caso, como a formiga está pendurada na borda do flange, a distância do centro da roda até a formiga é, na verdade, maior que o raio da roda (Figura\(\PageIndex{14}\)).

    A configuração aqui é essencialmente a mesma de quando a formiga subiu pelo raio na roda da bicicleta. Deixamos b indicar a distância do centro da roda até a formiga e deixamos que t represente o ângulo pelo qual o pneu girou. Além disso, deixamos\(C=(x_C,y_C)\) representar a posição do centro da roda e\(A=(x_A,y_A)\) representar a posição da formiga (Figura\( \PageIndex{14}\)).

    Quando a distância do centro da roda até a formiga é maior que o raio da roda, seu caminho de movimento é chamado de ciclóide prolato. Um gráfico de um ciclóide prolato é mostrado na figura.

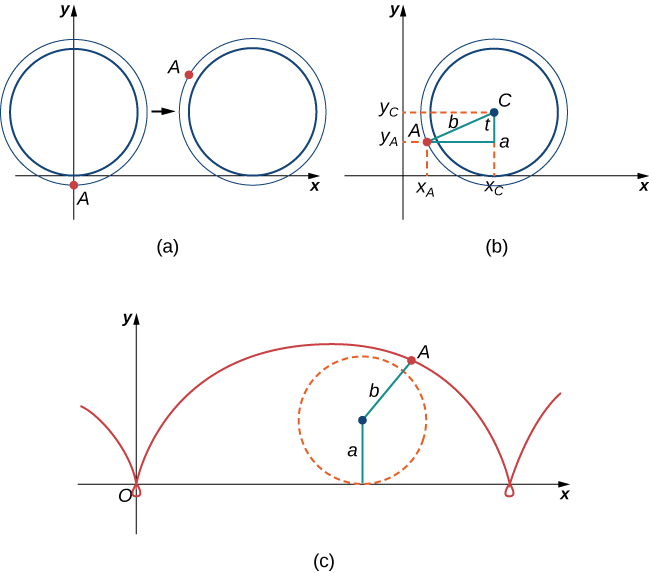
    Há três figuras marcadas (a), (b) e (c). A figura a tem um círculo e um ponto A que estão fora do círculo no eixo y (abaixo da origem). O círculo é tangente ao eixo x na origem. O círculo parece estar viajando para a direita no eixo x, com o ponto A acima do eixo x em uma segunda imagem do círculo desenhada ligeiramente à direita. A Figura b tem um círculo no primeiro quadrante com o centro C. Ela toca o eixo x em xc. Um ponto A é desenhado fora do círculo e um triângulo reto é formado a partir desse ponto e do ponto C. A hipotenusa é marcada com b, o ângulo em C entre A e xc é marcado como t e a distância de C a xc é marcada como a. As linhas são desenhadas para fornecer os valores x e y de A como xA e yA, respectivamente. Da mesma forma, uma linha é desenhada para fornecer o valor y de C como yC. A Figura c mostra a curva que o ponto A traçaria, à medida que o círculo viaja para a direita. É vagamente sinusoidal com um laço extra na parte inferior uma vez por rotação.
    Figura\(\PageIndex{14}\): (a) A formiga está pendurada no flange da roda do trem. (b) A nova configuração, agora que a formiga pulou na roda do trem. (c) A formiga viaja ao longo de um ciclóide prolato.

    4. Usando a mesma abordagem usada nas partes 1 a 3, encontre as equações paramétricas para o caminho do movimento da formiga.

    5. O que você percebe na sua resposta à parte 3 e na sua resposta à parte 4?

    Observe que a formiga está realmente viajando para trás às vezes (as “voltas” no gráfico), mesmo que o trem continue avançando. Ele provavelmente vai ficar muito tonto quando chegar em casa!

    Conceitos-chave

    • As equações paramétricas fornecem uma maneira conveniente de descrever uma curva. Um parâmetro pode representar o tempo ou alguma outra quantidade significativa.
    • Muitas vezes, é possível eliminar o parâmetro em uma curva parametrizada para obter uma função ou relação descrevendo essa curva.
    • Sempre há mais de uma maneira de parametrizar uma curva.
    • Equações paramétricas podem descrever curvas complicadas que são difíceis ou talvez impossíveis de descrever usando coordenadas retangulares.

    Glossário

    ciclóide
    a curva traçada por um ponto na borda de uma roda circular enquanto a roda rola ao longo de uma linha reta sem deslizar
    cúspide
    uma extremidade pontiaguda ou parte onde duas curvas se encontram
    orientação
    a direção em que um ponto se move em um gráfico à medida que o parâmetro aumenta
    parâmetro
    uma variável independente da qual\(y\) depende\(x\) e da qual depende em uma curva paramétrica; geralmente representada pela variável\(t\)
    curva paramétrica
    o gráfico das equações paramétricas\(x(t)\) e\(y(t)\) ao longo de um intervalo\(a≤t≤b\) combinado com as equações
    equações paramétricas
    as equações\(x=x(t)\) e\(y=y(t)\) que definem uma curva paramétrica
    parametrização de uma curva
    reescrevendo a equação de uma curva definida por uma função\(y=f(x)\) como equações paramétricas