11.1E: Exercícios para a Seção 11.1

Last updated
Save as PDF

Page ID: 187904

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 4, desenhe as curvas abaixo eliminando o parâmetro$t$. Dê a orientação da curva.

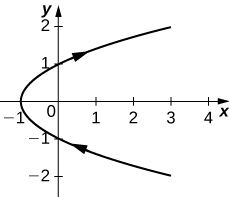
1)$ x=t^2+2t, \quad y=t+1$

Resposta

Orientação: de baixo para cima

$Uma parábola aberta para a direita com (−1, 0) sendo o ponto mais à esquerda com uma seta indo de baixo para (−1, 0) e para cima.$

2)$ x=\cos(t), \quad y=\sin(t), \quad \text{for } (0,2π]$

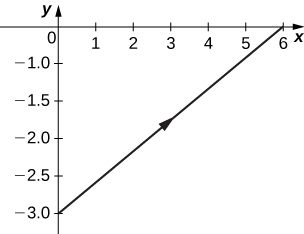
3)$ x=2t+4, \quad y=t−1$

Resposta

Orientação: da esquerda para a direita

$Uma linha reta passando por (0, −3) e (6, 0) com a seta apontando para cima e para a direita.$

4)$ x=3−t, \quad y=2t−3, \quad \text{for }1.5≤t≤3$

No exercício 5, elimine o parâmetro e desenhe o gráfico.

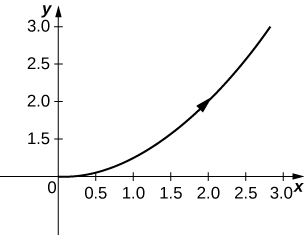
5)$x=2t^2,\quad y=t^4+1$

Resposta

$ y=\dfrac{x^2}{4}+1$

$Meia parábola começando na origem e passando por (2, 2) com a seta apontada para cima e para a direita.$

Nos exercícios 6 a 9, use a tecnologia (CAS ou calculadora) para esboçar as equações paramétricas.

6) [T]$x=t^2+t, \quad y=t^2−1$

7) [T]$ x=e^{−t}, \quad y=e^{2t}−1$

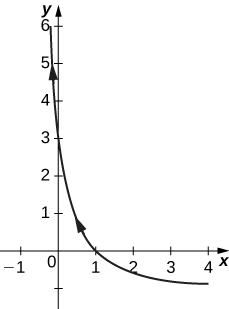
Resposta: $Uma curva passando por (1, 0) e (0, 3) com a seta apontando para cima e para a esquerda.$

8) [T]$ x=3\cos t, \quad y=4\sin t$

9) [T]$ x=\sec t, \quad y=\cos t$

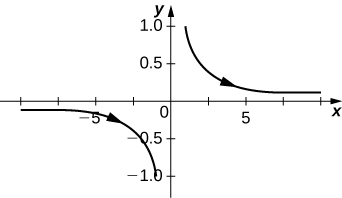
Resposta: $Um gráfico com assíntotas nos eixos x e y. Há uma parte do gráfico no terceiro quadrante com a seta apontando para baixo e para a direita. Há uma parte do gráfico no primeiro quadrante com a seta apontando para baixo e para a direita.$

Nos exercícios 10 a 20, esboce as equações paramétricas eliminando o parâmetro. Indique qualquer assíntota do gráfico.

10)$ x=e^t, \quad y=e^{2t}+1$

11)$ x=6\sin(2θ), \quad y=-4\cos(2θ)$

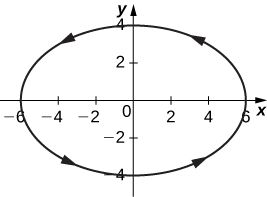
Resposta: $Uma elipse com eixo menor vertical e de comprimento 8 e eixo maior horizontal e de comprimento 12 que está centrada na origem. As setas vão no sentido anti-horário.$

12)$ x=\cos θ, \quad y=2\sin(2θ)$

13)$ x=3−2\cos θ, \quad y=−5+3\sin θ$

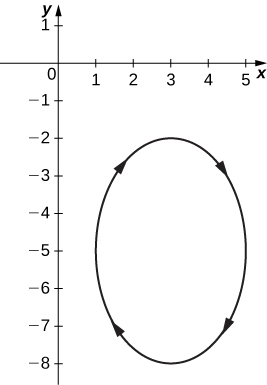
Resposta: $Uma elipse no quarto quadrante com eixo menor horizontal e de comprimento 4 e eixo maior vertical e de comprimento 6. As setas vão no sentido horário.$

14)$ x=4+2\cos θ, \quad y=−1+\sin θ$

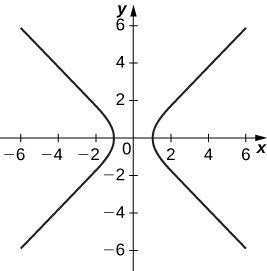
15)$ x=\sec t, \quad y=\tan t$

Resposta

As assíntotas são$ y=x$ e$ y=−x$

$Um gráfico com assíntotas em y = x e y = −x. A primeira parte do gráfico ocorre no segundo e terceiro quadrantes com vértice em (−1, 0). A segunda parte do gráfico ocorre no primeiro e quarto quadrantes com vértice como (1, 0).$

16)$ x=\ln(2t), \quad y=t^2$

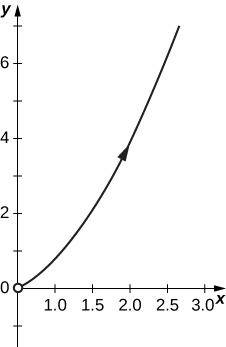
17)$ x=e^t, \quad y=e^{2t}$

Resposta: $Uma curva começando um pouco acima da origem e aumentando para a direita com a seta apontando para cima e para a direita.$

18)$ x=e^{−2t}, \quad y=e^{3t}$

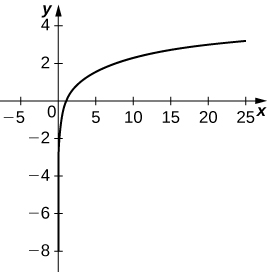
19)$ x=t^3, \quad y=3\ln t$

Resposta: $Uma curva com assíntota sendo o eixo y. A curva começa no quarto quadrante e aumenta rapidamente até (1, 0), ponto em que aumenta muito mais lentamente.$

20)$ x=4\sec θ, \quad y=3\tan θ$

Nos exercícios 21 a 38, converta as equações paramétricas de uma curva em forma retangular. Nenhum esboço é necessário. Indique o domínio da forma retangular.

21)$ x=t^2−1, \quad y=\dfrac{t}{2}$

Resposta: $ x=4y^2−1;$domínio:$ x∈[1,∞)$.

22)$ x=\dfrac{1}{\sqrt{t+1}}, \quad y=\dfrac{t}{1+t}, \quad \text{for }t>−1$

23)$ x=4\cos θ, \quad y=3\sin θ, \quad \text{for }t∈(0,2π]$

Resposta: $ \dfrac{x^2}{16}+\dfrac{y^2}{9}=1;$domínio$ x∈[−4,4].$

24)$ x=\cosh t, \quad y=\sinh t$

25)$ x=2t−3, \quad y=6t−7$

Resposta: $ y=3x+2;$domínio: todos os números reais.

26)$ x=t^2, \quad y=t^3$

27)$ x=1+\cos t, \quad y=3−\sin t$

Resposta: $ (x−1)^2+(y−3)^2=1$; domínio:$ x∈[0,2]$.

28)$ x=\sqrt{t}, \quad y=2t+4$

29)$ x=\sec t, \quad y=\tan t, \quad \text{for } π≤t<\frac{3π}{2}$

Resposta: $ y=\sqrt{x^2−1}$; domínio:$ x∈(−\infty,-1]$.

30)$ x=2\cosh t, \quad y=4\sinh t$

31)$ x=\cos(2t), \quad y=\sin t$

Resposta: $ y^2=\dfrac{1−x}{2};$domínio:$ x∈[-1,1].$

32)$ x=4t+3, \quad y=16t^2−9$

33)$ x=t^2, \quad y=2\ln t, \quad \text{for }t≥1$

Resposta: $ y=\ln x;$domínio:$ x∈[1,∞).$

34)$ x=t^3, \quad y=3\ln t, \quad \text{for }t≥1$

35)$ x=t^n, \quad y=n\ln t, \quad \text{for } t≥1,$ onde$n$ está um número natural

Resposta: $ y=\ln x;$domínio:$ x∈(0,∞).$

36)$ x=\ln(5t), \quad y=\ln(t^2)$ onde$ 1≤t≤e$

37)$ x=2\sin(8t), \quad y=2\cos(8t)$

Resposta: $ x^2+y^2=4;$domínio:$ x∈[−2,2].$

38)$ x=\tan t, \quad y=\sec^2t−1$

Nos exercícios 39 a 48, os pares de equações paramétricas representam linhas, parábolas, círculos, elipses ou hipérboles. Nomeie o tipo de curva básica que cada par de equações representa.

39)$ x=3t+4, \quad y=5t−2$

Resposta: linha

40)$ x−4=5t, \quad y+2=t$

41)$ x=2t+1, \quad y=t^2−3$

Resposta: parábola

(42)$ x=3\cos t, \quad y=3\sin t$

43)$ x=2\cos(3t), \quad y=2\sin(3t)$

Resposta: circular

44)$ x=\cosh t, \quad y=\sinh t$

45)$ x=3\cos t, \quad y=4\sin t$

Resposta: elipse

(46)$ x=2\cos(3t), \quad y=5\sin(3t)$

47)$ x=3\cosh(4t) \quad y=4\sinh(4t)$

Resposta: o ramo direito de uma hipérbole que se abre horizontalmente

48)$ x=2\cosh t, \quad y=2\sinh t$

49) Mostre que$ x=h+r\cos θ, \quad y=k+r\sin θ$ representa a equação de um círculo.

50) Use as equações do problema anterior para encontrar um conjunto de equações paramétricas para uma circunferência cujo raio é$5$ e cujo centro é$ (−2,3)$.

Nos exercícios 51 a 53, use um utilitário gráfico para representar graficamente a curva representada pelas equações paramétricas e identificar a curva a partir de sua equação.

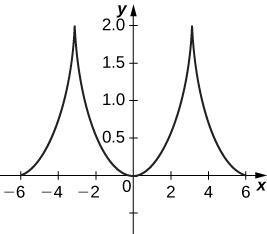
51) [T]$ x=θ+\sin θ, \quad y=1−\cos θ$

Resposta

As equações representam um ciclóide.

$Um gráfico começando em (−6, 0) aumentando rapidamente até um ponto nítido em (−3, 2) e depois diminuindo rapidamente até a origem. O gráfico é simétrico em relação ao eixo y, então o gráfico aumenta rapidamente para (3, 2) antes de diminuir rapidamente para (6, 0).$

52) [T]$ x=2t−2\sin t, \quad y=2−2\cos t$

53) [T]$ x=t−0.5\sin t, \quad y=1−1.5\cos t$

Resposta: $Um gráfico começando em aproximadamente (−6, 0) aumentando para um ponto arredondado e depois diminuindo para aproximadamente (0, −0,5). O gráfico é simétrico em relação ao eixo y, então o gráfico aumenta para um ponto arredondado antes de diminuir para aproximadamente (6, 0).$

54) Um avião viajando horizontalmente a 100 m/s sobre solo plano a uma altitude de 4000 metros deve lançar um pacote de emergência em um alvo no solo. A trajetória da embalagem é dada por$ x=100t, \quad y=−4.9t^2+4000, \quad \text{where }t≥0$ onde a origem é o ponto no solo diretamente abaixo do plano no momento da liberação. Quantos metros horizontais antes do alvo o pacote deve ser liberado para atingir o alvo?

55) A trajetória de uma bala é dada por$ x=v_0(\cos α)t, \quad y=v_0(\sin α)t−\frac{1}{2}gt^2$ onde$ v_0=500$ m/s,$g=9.8=9.8\text{ m/s}^2$, e$ α=30$ graus. Quando a bala atingirá o chão? A que distância da arma a bala atingirá o chão?

Resposta: 22.092 metros em aproximadamente 51 segundos.

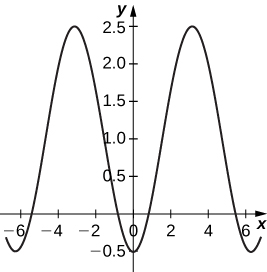
56) [T] Use a tecnologia para esboçar a curva representada por$ x=\sin(4t), \quad y=\sin(3t), \quad \text{for }0≤t≤2π$.

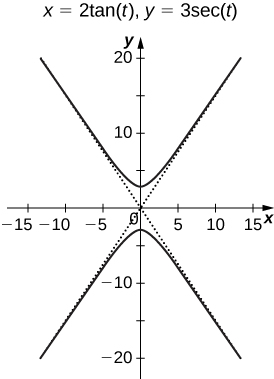
57) [T] Use a tecnologia para esboçar$ x=2\tan(t), \quad y=3\sec(t), \quad \text{for }−π<t<π.$

Resposta: $Um gráfico com assíntotas aproximadamente perto de y = x e y = −x. A primeira parte do gráfico está no primeiro e segundo quadrantes com vértice próximo (0, 3). A segunda parte do gráfico está no terceiro e quarto quadrantes com o vértice próximo (0, −3).$

58) Esboce a curva conhecida como epitrocóide, que fornece o caminho de um ponto em um círculo de raio$b$ à medida que ele rola para fora de um círculo de raio$a$. As equações são

$ x=(a+b)\cos t−c⋅\cos\left[\frac{(a+b)t}{b}\right], \quad y=(a+b)\sin t−c⋅\sin\left[\frac{(a+b)t}{b}\right]$.

Deixe$ a=1,\;b=2,\;c=1.$

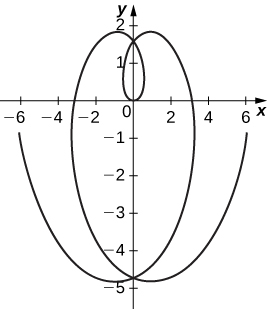
59) [T] Use a tecnologia para esboçar a curva espiral dada$ x=t\cos(t), \quad y=t\sin(t)$ por for$ −2π≤t≤2π.$

Resposta: $Um gráfico começando em aproximadamente (−6, −1) diminuindo ao mínimo no terceiro quadrante próximo a (−1, −4,8) aumentando aproximadamente (0, −4,7) e (3, 0) até um máximo próximo (1, 1,9) antes de diminuir até (0, 1,5) até a origem. O gráfico é simétrico em relação ao eixo y, então o gráfico aumenta até (0, 1,5) até um máximo no segundo quadrante, diminui novamente em (0, −4,7) e depois aumenta para (6, −1).$

60) [T] Use a tecnologia para representar graficamente a curva dada pelas equações paramétricas$ x=2\cot(t), \quad y=1−\cos(2t), \quad \text{for }−π/2≤t≤π/2.$ Esta curva é conhecida como a bruxa de Agnesi.

61) [T] Esboce a curva dada pelas equações paramétricas$ x=\cosh(t), \quad y=\sinh(t),$ para$ −2≤t≤2.$

Resposta: $Um grafo vagamente parabólico com vértice no ponto (1, 0) que se abre para a direita.$