8.6: Exercícios de revisão do capítulo 8

Last updated
Save as PDF

Page ID: 188053

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Verdadeiro ou falso? Justifique sua resposta com uma prova ou um contra-exemplo.

1) A equação diferencial$y'=3x^2y−\cos(x)y''$ é linear.

2) A equação diferencial$y'=x−y$ é separável.

Responda: $F$

3) Você pode resolver explicitamente todas as equações diferenciais de primeira ordem por separação ou pelo método de integração de fatores.

4) Você pode determinar o comportamento de todas as equações diferenciais de primeira ordem usando campos direcionais ou o método de Euler.

Responda: $T$

Para os problemas a seguir, encontre a solução geral para as equações diferenciais.

5)$y′=x^2+3e^x−2x$

6)$y'=2^x+\cos^{−1}x$

Responda: $y(x)=\frac{2^x}{ln(2)}+xcos^{−1}x−\sqrt{1−x^2}+C$

7)$y'=y(x^2+1)$

8)$y'=e^{−y}\sin x$

Responda: $y(x)=\ln(C−\cos x)$

9)$y'=3x−2y$

10)$y'=y\ln y$

Responda: $y(x)=e^{e^{C+x}}$

Para os problemas a seguir, encontre a solução para o problema do valor inicial.

11)$y'=8x−\ln x−3x^4, \quad y(1)=5$

12)$y'=3x−\cos x+2, \quad y(0)=4$

Responda: $y(x)=4+\frac{3}{2}x^2+2x−\sin x$

13)$xy'=y(x−2), \quad y(1)=3$

14)$y'=3y^2(x+\cos x), \quad y(0)=−2$

Responda: $y(x)=−\dfrac{2}{1+3(x^2+2\sin x)}$

15)$(x−1)y'=y−2, \quad y(0)=0$

16)$y'=3y−x+6x^2, \quad y(0)=−1$

Responda: $y(x)=−2x^2−2x−\frac{1}{3}−\frac{2}{3}e^{3x}$

Para os problemas a seguir, desenhe o campo direcional associado à equação diferencial e resolva a equação diferencial. Desenhe uma solução de amostra no campo direcional.

17)$y'=2y−y^2$

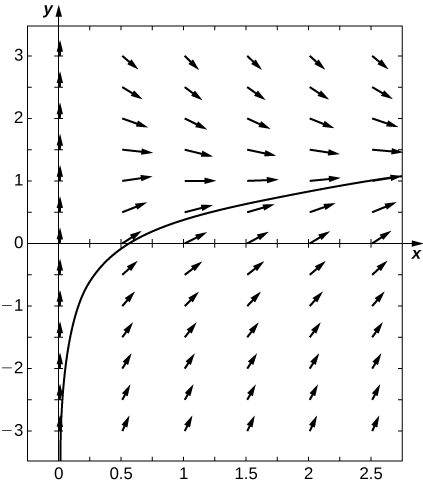
18)$y'=\dfrac{1}{x}+\ln x−y,$ para$x>0$

Responda

$y(x)=Ce^{−x}+\ln x$

$Um campo de direção com setas apontando para cima e para a direita ao longo de uma curva logarítmica que se aproxima do infinito negativo quando x vai para zero e aumenta à medida que x vai para o infinito.$

Para os problemas a seguir, use o Método de Euler com$n=5$ etapas ao longo do intervalo.$t=[0,1].$ Em seguida, resolva exatamente o problema do valor inicial. Qual é a proximidade da estimativa do Método de Euler?

19)$y'=−4yx, \quad y(0)=1$

20)$y'=3^x−2y, \quad y(0)=0$

Responda: Euler:$0.6939$, Solução
exata:$y(x)=\dfrac{3^x−e^{−2x}}{2+\ln(3)}$

Para os problemas a seguir, configure e resolva as equações diferenciais.

21) Um carro dirige por uma rodovia, acelerando de acordo com$a=5\sin(πt),$ onde$t$ representa o tempo em minutos. Encontre a velocidade a qualquer momento$t$, supondo que o carro dê partida com uma velocidade inicial de$60$ mph.

22) Você joga uma bola de$2$ quilogramas de massa no ar com uma velocidade ascendente de$8$ m/s. Encontre exatamente o tempo em que a bola permanecerá no ar, assumindo que a gravidade é dada por$g=9.8\,\text{m/s}^2$.

Responda: $\frac{40}{49}$segundo

23) Você joga uma bola com uma massa de$5$ quilos pela janela de um avião a uma altura de$5000$ m. Quanto tempo a bola leva para chegar ao chão?

24) Você derruba a mesma bola de$5$ quilogramas de massa da mesma janela do avião na mesma altura, exceto que desta vez você assume uma força de arrasto proporcional à velocidade da bola, usando uma constante de proporcionalidade de$3$ e a bola atinge a velocidade terminal. Resolva a distância percorrida em função do tempo. Quanto tempo a bola leva para chegar ao chão?

Responda: $x(t)=5000+\frac{245}{9}−\frac{49}{3}t−\frac{245}{9}e^{−5/3t}, \quad t=307.8$segundos

25) Um medicamento é administrado a um paciente a cada$24$ hora e é eliminado a uma taxa proporcional à quantidade de medicamento restante no corpo, com proporcionalidade constante$0.2$. Se o paciente precisar que um nível basal de$5$ mg esteja sempre na corrente sanguínea, qual deve ser a dose?

26) Um tanque$1000$ de 1 litro contém água pura e uma solução de$0.2$ kg de sal/L é bombeada para o tanque a uma taxa de$1$ L/min e é drenada na mesma taxa. Resolva a quantidade total de sal no tanque de cada vez$t$.

Responda: $T(t)=200\left(1−e^{−t/1000}\right)$

27) Você ferve água para fazer chá. Quando você despeja a água no bule, a temperatura é$100°C.$ Depois de$5$ minutos no seu$15°C$ quarto, a temperatura do chá é$85°C$. Resolva a equação para determinar as temperaturas do chá por vez$t$. Quanto tempo você deve esperar até que o chá esteja em uma temperatura potável ($72°C$)?

28) A população humana (em milhares) de Nevada em$1950$ era de aproximadamente$160$. Se a capacidade de carga for estimada em$10$ milhões de indivíduos e assumindo uma taxa de crescimento$2\%$ por ano, desenvolva um modelo de crescimento logístico e resolva o problema para a população em Nevada a qualquer momento (use$1950$ como tempo = 0). Para qual população seu modelo prevê$2000$? Quão perto está sua previsão do verdadeiro valor de$1,998,257$?

Responda: $P(t)=\dfrac{1600000e^{0.02t}}{9840+160e^{0.02t}}$

29) Repita o problema anterior, mas use o modelo de crescimento de Gompertz. O que é mais preciso?