7.6: Integração numérica
- Page ID
- 188251
- Aproxime o valor de uma integral definida usando as regras do ponto médio e do trapezoidal.
- Determine o erro absoluto e relativo ao usar uma técnica de integração numérica.
- Estime o erro absoluto e relativo usando uma fórmula vinculada ao erro.
- Reconheça quando o ponto médio e as regras trapezoidais superestimam ou subestimam o valor real de uma integral.
- Use a regra de Simpson para aproximar o valor de uma integral definida a uma determinada precisão.
As antiderivadas de muitas funções não podem ser expressas ou não podem ser expressas facilmente de forma fechada (ou seja, em termos de funções conhecidas). Consequentemente, em vez de avaliar integrais definidas dessas funções diretamente, recorremos a várias técnicas de integração numérica para aproximar seus valores. Nesta seção, exploramos várias dessas técnicas. Além disso, examinamos o processo de estimar o erro no uso dessas técnicas.
A regra do ponto médio
Anteriormente neste texto, definimos a integral definida de uma função em um intervalo como o limite das somas de Riemann. Em geral, qualquer soma de Riemann de uma função\( f(x)\) em um intervalo\([a,b]\) pode ser vista como uma estimativa de\(\displaystyle ∫^b_af(x)\,dx\). Lembre-se de que a soma de Riemann de uma função\( f(x)\) em um intervalo\( [a,b]\) é obtida selecionando uma partição.
\[ P=\{x_0,x_1,x_2,…,x_n\} \nonumber \]
onde\(\quad a=x_0<x_1<x_2<⋯<x_n=b \)
e um conjunto
\[ S=\{x^*_1,x^*_2,…,x^*_n\} \nonumber \]
onde\(x_{i−1}≤x^*_i≤x_i \quad \text{for all} \, i.\)
A soma de Riemann correspondente à partição\(P\) e ao conjunto\(S\) é dada por\(\displaystyle \sum^n_{i=1}f(x^*_i)Δx_i\), onde\( Δx_i=x_i−x_{i−1},\) o comprimento do\( i^{\text{th}}\) subintervalo.
A regra do ponto médio para estimar uma integral definida usa uma soma de Riemann com subintervalos de igual largura e os pontos médios,\( m_i\), de cada subintervalo no lugar de\( x^*_i\). Formalmente, declaramos um teorema sobre a convergência da regra do ponto médio da seguinte forma.
Suponha que\( f(x)\) seja contínuo\([a,b]\). \( n\)Seja um número inteiro positivo\( Δx=\dfrac{b−a}{n}\) e. Se\( [a,b]\) for dividido em\( n\) subintervalos, cada um de comprimento\( Δx\) e\( m_i\) for o ponto médio do\( i^{\text{th}}\) subintervalo, defina
\[M_n=\sum_{i=1}^nf(m_i)Δx. \nonumber \]
Então\(\displaystyle \lim_{n→∞}M_n=∫^b_af(x)\,dx.\)
Como podemos ver na Figura\(\PageIndex{1}\), se\( f(x)≥0\) terminar\( [a,b]\), então\(\displaystyle \sum^n_{i=1}f(m_i)Δx\) corresponde à soma das áreas dos retângulos que se aproximam da área entre o gráfico de\( f(x)\) e o\(x\) eixo -acima\([a,b]\). O gráfico mostra os retângulos correspondentes a\(M_4\) uma função não negativa em um intervalo fechado.\([a,b].\)
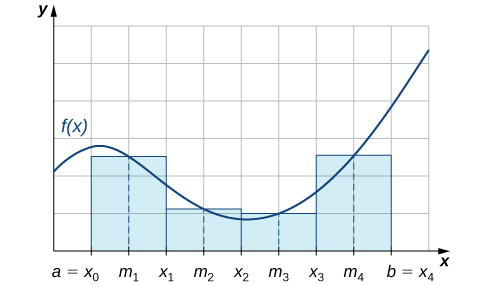
Use a regra do ponto médio para estimar\(\displaystyle ∫^1_0x^2\,dx\) usando quatro subintervalos. Compare o resultado com o valor real dessa integral.
Solução: Cada subintervalo tem comprimento\( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Portanto, os subintervalos consistem em
\[\left[0,\tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2},\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right].\nonumber \]
Os pontos médios desses subintervalos são\(\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right\}.\) Assim,
\[\begin{align*} M_4 &=\frac{1}{4}\cdot f\left(\frac{1}{8}\right)+\frac{1}{4}\cdot f\left(\frac{3}{8}\right)+\frac{1}{4}\cdot f\left(\frac{5}{8}\right)+\frac{1}{4}\cdot f\left(\frac{7}{8}\right) \\[4pt] &=\frac{1}{4}⋅\frac{1}{64}+\frac{1}{4}⋅\frac{9}{64}+\frac{1}{4}⋅\frac{25}{64}+\frac{1}{4}⋅\frac{49}{64}\\[4pt] &=\frac{21}{64} = 0.328125. \end{align*}\]
Desde
\[ ∫^1_0x^2\,dx=\frac{1}{3},\nonumber \]
o erro absoluto nessa aproximação é:
\[\left\lvert\dfrac{1}{3}−\dfrac{21}{64}\right\rvert=\dfrac{1}{192}≈0.0052, \nonumber \]
e vemos que a regra do ponto médio produz uma estimativa que é um pouco próxima do valor real da integral definida.
Use\(M_6\) para estimar o comprimento da curva\(y=\frac{1}{2}x^2\) em\([1,4]\).
Solução: O comprimento de\(y=\frac{1}{2}x^2\) um\([1,4]\) é
\[s = ∫^4_1\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx.\nonumber \]
Uma vez que\(\dfrac{dy}{dx}=x\), essa integral se torna\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx.\)
Se\([1,4]\) for dividido em seis subintervalos, então cada subintervalo tem comprimento\(Δx=\dfrac{4−1}{6}=\dfrac{1}{2}\) e os pontos médios dos subintervalos são\(\left\{\frac{5}{4},\frac{7}{4},\frac{9}{4},\frac{11}{4},\frac{13}{4},\frac{15}{4}\right\}\). Se definirmos\(f(x)=\sqrt{1+x^2}\),
\[\begin{align*} M_6 &=\tfrac{1}{2}\cdot f\left(\frac{5}{4}\right)+\tfrac{1}{2}\cdot f\left(\frac{7}{4}\right)+\frac{1}{2}\cdot f\left(\frac{9}{4}\right)+\frac{1}{2}\cdot f\left(\frac{11}{4}\right)+\frac{1}{2}\cdot f\left(\frac{13}{4}\right)+\frac{1}{2}\cdot f\left(\frac{15}{4}\right) \\[4pt] &≈\frac{1}{2}(1.6008+2.0156+2.4622+2.9262+3.4004+3.8810)=8.1431 \, \text{ units}. \end{align*}\]
Use a regra do ponto médio com\( n=2\) para estimar\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Dica
-
\( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)
- Resposta
-
\(\dfrac{24}{35}\approx 0.685714\)
A regra trapezoidal
Também podemos aproximar o valor de uma integral definida usando trapézios em vez de retângulos. Na Figura\(\PageIndex{2}\), a área abaixo da curva é aproximada por trapézios em vez de retângulos.
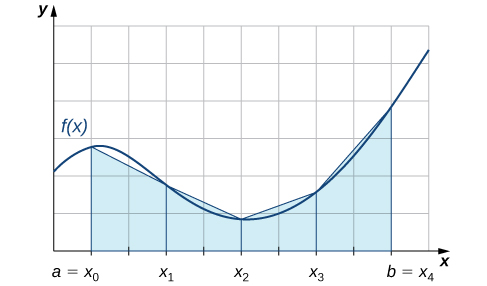
A regra trapezoidal para estimar integrais definidas usa trapézios em vez de retângulos para aproximar a área sob uma curva. Para obter informações sobre a forma final da regra, considere os trapézios mostrados na Figura\(\PageIndex{2}\). Assumimos que a duração de cada subintervalo é dada por\(Δx\). Primeiro, lembre-se de que a área de um trapézio com altura\(h\) e bases de comprimento\(b_1\)\(b_2\) é dada por\(\text{Area}=\frac{1}{2}h(b_1+b_2)\). Vemos que o primeiro trapézio tem uma altura\(Δx\) e bases paralelas de comprimento\( f(x_0)\)\( f(x_1)\) e. Assim, a área do primeiro trapézio na Figura\(\PageIndex{2}\) é
\[ \frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big).\nonumber \]
As áreas dos três trapézios restantes são
\(\dfrac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big),\, \dfrac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big),\)e\( \dfrac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\)
Consequentemente,
\[∫^b_af(x)\,dx≈\frac{1}{2}Δx\Big(f(x_0)+f(x_1)\Big)+\frac{1}{2}Δx\Big(f(x_1)+f(x_2)\Big)+\frac{1}{2}Δx\Big(f(x_2)+f(x_3)\Big)+\frac{1}{2}Δx\Big(f(x_3)+f(x_4)\Big).\nonumber \]
Depois de retirar um fator comum\(\frac{1}{2}Δx\) e combinar termos semelhantes, temos
\[ ∫^b_af(x)\,dx≈\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f(x_4)\Big].\nonumber \]
Generalizando, declaramos formalmente a seguinte regra.
Suponha que\(f(x)\) seja um fim contínuo\([a,b]\). \(n\)Seja um número inteiro positivo\(Δx=\dfrac{b−a}{n}\) e. Vamos\( [a,b]\) ser divididos em\(n\) subintervalos, cada um de comprimento\(Δx\), com pontos finais em\( P=\{x_0,x_1,x_2…,x_n\}.\)
Definir
\[T_n=\frac{Δx}{2}\Big[f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Em seguida,\(\displaystyle \lim_{n→+∞}T_n=∫^b_af(x)\,dx.\)
Antes de continuar, vamos fazer algumas observações sobre a regra trapezoidal. Em primeiro lugar, é útil observar que
\(T_n=\dfrac{1}{2}(L_n+R_n)\)onde\(\displaystyle L_n=\sum_{i=1}^nf(x_{i−1})Δx\) e\(\displaystyle R_n=\sum_{i=1}^nf(x_i)Δx.\)
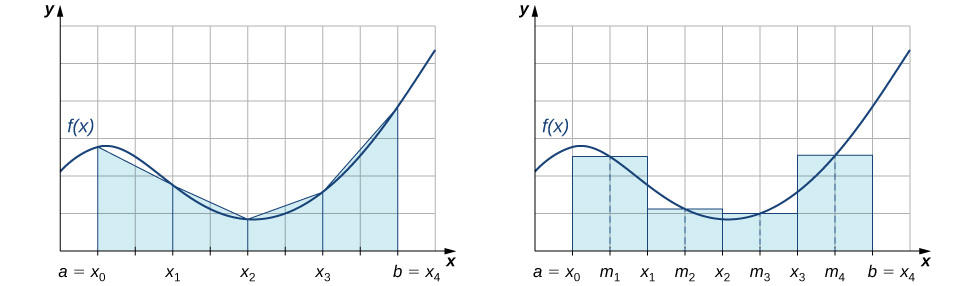
Ou seja,\(L_n\)\(R_n\) aproxime a integral usando as extremidades esquerda e direita de cada subintervalo, respectivamente. Além disso, um exame cuidadoso da Figura nos\(\PageIndex{3}\) leva a fazer as seguintes observações sobre o uso das regras trapezoidais e do ponto médio para estimar a integral definida de uma função não negativa. A regra trapezoidal tende a superestimar o valor de uma integral definida sistematicamente em intervalos em que a função é côncava para cima e a subestimar o valor de uma integral definida sistematicamente em intervalos em que a função é côncava para baixo. Por outro lado, a regra do ponto médio tende a calcular a média desses erros, superestimando parcialmente e subestimando parcialmente o valor da integral definida nesses mesmos tipos de intervalos. Isso nos leva a hipotetizar que, em geral, a regra do ponto médio tende a ser mais precisa do que a regra trapezoidal.
Use a regra trapezoidal para estimar\(\displaystyle ∫^1_0x^2\,dx\) usando quatro subintervalos.
Solução
Os pontos finais dos subintervalos consistem em elementos do conjunto\(P=\left\{0,\frac{1}{4},\, \frac{1}{2},\, \frac{3}{4},1\right\}\) e,\(Δx=\frac{1−0}{4}=\frac{1}{4}.\) portanto,
\ [\ begin {align*} ^1_0x^2dx &≈\ frac {1} {2}\ frac {1} {4}\ Big [f (0) +2\, f\ left (\ tfrac {1} {4}\ direita) +2\, f\ left (\ tfrac {1} {2}\ direita) +2\, f\ esquerda (\ tfrac {1} {2}\ direita) +2\, f\ esquerda (\ tfrac {1} {2}\ direita) +2\, f\ esquerda (\ tfrac {1} {2}\ tfrac {3} {4}\ direita) +f (1)\ Grande]\\ [4pt]
&=\ tfrac {1} {8}\ big (0+2₽\ tfrac {1} {16} +2\ tfrac {1} {4} +2⁄tfrac {9} {16} +1\ big)\\[4pt] &=\frac{11}{32} = 0.34375\end{align*}\]
Use a regra trapezoidal com\( n=2\) para estimar\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Dica
-
Conjunto\(Δx=\dfrac{1}{2}.\) Os pontos finais dos subintervalos são os elementos do conjunto\(P=\left\{1,\frac{3}{2},2\right\}.\)
- Resposta
-
\(\dfrac{17}{24} \approx 0.708333\)
Erro absoluto e relativo
Um aspecto importante do uso dessas regras de aproximação numérica consiste em calcular o erro ao usá-las para estimar o valor de uma integral definida. Primeiro, precisamos definir erro absoluto e erro relativo.
Se\(B\) for nossa estimativa de alguma quantidade com um valor real de\(A\), então o erro absoluto é dado por\(|A−B|\).
O erro relativo é o erro como uma porcentagem do valor real e é dado por\[\left\lvert\frac{A−B}{A}\right\rvert⋅100\%. \nonumber \]
Calcule o erro absoluto e relativo na estimativa do\(\displaystyle ∫^1_0x^2\,dx\) uso da regra do ponto médio, encontrada em Exemplo\(\PageIndex{1}\).
Solução: O valor calculado é\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) e nossa estimativa do exemplo é\(M_4=\frac{21}{64}\). Assim, o erro absoluto é dado por\(\left\lvert\frac{1}{3}−\frac{21}{64}\right\rvert=\frac{1}{192}≈0.0052.\)
O erro relativo é\[\frac{1/192}{1/3}=\frac{1}{64}≈0.015625≈1.6\%.\nonumber \]
Calcule o erro absoluto e relativo na estimativa do\(\displaystyle ∫^1_0x^2\,dx\) uso da regra trapezoidal, encontrada em Exemplo\(\PageIndex{3}\).
Solução: O valor calculado é\(\displaystyle ∫^1_0x^2\,dx=\frac{1}{3}\) e nossa estimativa do exemplo é\(T_4=\frac{11}{32}\). Assim, o erro absoluto é dado por\(\left\lvert\frac{1}{3}−\frac{11}{32}\right\rvert=\frac{1}{96}≈0.0104.\)
O erro relativo é dado por\[\frac{1/96}{1/3}=0.03125≈3.1\%.\nonumber \]
Em um ponto de verificação anterior, estimamos\(\displaystyle ∫^2_1\frac{1}{x}\,dx\) estar\(\frac{24}{35}\) usando\(M_2\). O valor real dessa integral é\(\ln 2\). Usando\(\frac{24}{35}≈0.6857\) e\(\ln 2≈0.6931,\) calculando o erro absoluto e o erro relativo.
- Dica
-
Use os exemplos anteriores como guia.
- Resposta
-
erro absoluto\(\approx 0.0074,\) e erro relativo\(\approx 1.1\%\)
Limites de erro no ponto médio e nas regras trapezoidais
Nos dois exemplos anteriores, pudemos comparar nossa estimativa de uma integral com o valor real da integral; no entanto, normalmente não temos esse luxo. Em geral, se estamos nos aproximando de uma integral, estamos fazendo isso porque não podemos calcular facilmente o valor exato da integral em si. Portanto, muitas vezes é útil poder determinar um limite superior para o erro na aproximação de uma integral. O teorema a seguir fornece limites de erro para as regras do ponto médio e do trapezoidal. O teorema é declarado sem prova.
\(f(x)\)Seja uma função contínua encerrada\([a,b]\), tendo uma segunda\(f''(x)\) derivada nesse intervalo. Se\(M\) for o valor máximo de\(|f''(x)|\) mais\([a,b]\), então os limites superiores para o erro no uso\(M_n\) e\(T_n\) na estimativa\(\displaystyle ∫^b_af(x)\,dx\) são
\[\text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}\label{MidError} \]
e
\[\text{Error in}\, T_n≤\frac{M(b−a)^3}{12n^2} \nonumber \].
Podemos usar esses limites para determinar o valor\(n\) necessário para garantir que o erro em uma estimativa seja menor do que um valor especificado.
Qual valor de\(n\) deve ser usado para garantir que uma estimativa de\(\displaystyle ∫^1_0e^{x^2}\,dx\) seja precisa dentro\(0.01\) se usarmos a regra do ponto médio?
Solução
Começamos determinando o valor de\(M\), o valor máximo de\( |f''(x)|\) over\( [0,1]\) for\( f(x)=e^{x^2}\). Uma vez\( f′(x)=2xe^{x^2},\) que temos
\[ f''(x)=2e^{x^2}+4x^2e^{x^2}.\nonumber \]
Assim,
\[ |f''(x)|=2e^{x^2}(1+2x^2)≤2⋅e⋅3=6e.\nonumber \]
A partir da equação vinculada a erros\(\ref{MidError}\), temos
\[ \text{Error in}\, M_n≤\frac{M(b−a)^3}{24n^2}≤\frac{6e(1−0)^3}{24n^2}=\frac{6e}{24n^2}.\nonumber \]
Agora resolvemos a seguinte desigualdade para\(n\):
\[\frac{6e}{24n^2}≤0.01.\nonumber \]
Assim, uma\(n≥\sqrt{\frac{600e}{24}}≈8.24.\) vez que\(n\) deve ser um número inteiro satisfazendo essa desigualdade, uma escolha de\(n=9\) garantiria que
\[ \left\lvert ∫^1_0e^{x^2}\,dx−M_n \right\rvert <0.01.\nonumber \]
Análise
Talvez tenhamos sido tentados a arredondar para\(8.24\) baixo e escolher\(n=8\), mas isso seria incorreto porque devemos ter um número inteiro maior ou igual\(8.24\) a. Precisamos ter em mente que as estimativas de erro fornecem um limite superior somente para o erro. A estimativa real pode, de fato, ser uma aproximação muito melhor do que a indicada pelo limite de erro.
Use a Equação\(\ref{MidError}\) para encontrar um limite superior para o erro de uso\(M_4\) para estimar\(\displaystyle ∫^1_0x^2\,dx.\)
- Dica
-
\(f''(x)=2,\)então\(M=2.\)
- Resposta
-
\(\dfrac{1}{192}\)
Regra de Simpson
Com a regra do ponto médio, estimamos áreas de regiões sob curvas usando retângulos. Em certo sentido, aproximamos a curva com funções constantes por partes. Com a regra trapezoidal, aproximamos a curva usando funções lineares por partes. E se, em vez disso, aproximássemos uma curva usando funções quadráticas por partes? Com a regra de Simpson, fazemos exatamente isso. Nós dividimos o intervalo em um número par de subintervalos, cada um com a mesma largura. No primeiro par de subintervalos, nos aproximamos\(\displaystyle ∫^{x_2}_{x_0}f(x)\,dx\) de\(\displaystyle ∫^{x_2}_{x_0}p(x)\,dx\), onde\(p(x)=Ax^2+Bx+C\) está a função quadrática passando por\((x_0,f(x_0)), \,(x_1,f(x_1)),\) e\((x_2,f(x_2))\) (Figura\(\PageIndex{4}\)). No próximo par de subintervalos,\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) aproximamos a integral de outra função quadrática passando\( (x_2,f(x_2)), \,(x_3,f(x_3)),\) e\((x_4,f(x_4)).\) esse processo é continuado com cada par sucessivo de subintervalos.
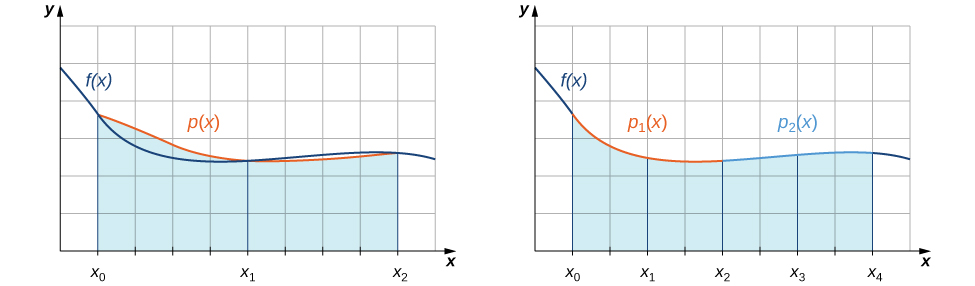
Para entender a fórmula que obtemos para a regra de Simpson, começamos derivando uma fórmula para essa aproximação nos dois primeiros subintervalos. À medida que analisamos a derivação, precisamos ter em mente as seguintes relações:
\[f(x_0)=p(x_0)=Ax_0^2+Bx_0+C \nonumber \]
\[f(x_1)=p(x_1)=Ax_1^2+Bx_1+C \nonumber \]
\[f(x_2)=p(x_2)=Ax_2^2+Bx_2+C \nonumber \]
\(x_2−x_0=2Δx\), onde\(Δx\) é a duração de um subintervalo.
\(x_2+x_0=2x_1,\)desde\(x_1=\dfrac{(x_2+x_0)}{2}\).
Assim,
\ [\ begin {align*} ^ {x_2} _ {x_0} f (x)\, dx &≈ ^ {x_2} _ {x_0} p (x)\, dx\\ [4pt]
&=^ {x_2} _ {x_0} (Ax^2+Bx+C)\, dx\\ [4pt]
&=\ left (\ frac {A} {3} x^3+\ frac {B} {2} x^2+cx\ right)\ bigg|^ {x_2} _ {x_0} & &\ text {Encontre a antiderivada.}\\ [4pt]
&=\ frac {A} {3} (x_2^3−x_0^3) +\ frac {B} {2} (x_2^2−x_0^2) +C (x_2−x_0) & &\ text {Avalie a antiderivada.}\\ [4pt]
&=\ frac {A} {3} (x_2−x_0) (x_2^2+x_2x_0+x_0^2)\ frac c {B} {2} (x_2−x_0) (x_2+x_0) +C (x_2−x_0)\\ [4pt]
&=\ frac {x_2−x_0} {6}\ bigg (2A (x_2^2+x_2x_0+x_0^2) +3B (x_2+x_x_0^2) +3B (x_2+x_x_0^2) 0) +6C\ bigg) & &\ text {Fator fora}\,\ frac {x_2−x_0} {6}.\\ [4pt]
&=\ frac {Δx} {3}\ bigg ((Ax_2^2+Bx_2+C) + (Ax_0^2+Bx_0+C) +A (x_2^2+2x_2x_0+x_0^2) +2B (x_2+x_0) +4C\ bigg) & &\ text {Reorganize os termos. Nota:}\ enspace Δx =\ frac {x_2−x_0} {2}\\ [4pt]
&=\ frac {Δx} {3}\ big (f (x_2) +f (x_0) +A (x_2+x_0) ^2+2B (x_2+x_0) +4C\ big) &\ text {Fator e substitua:}\\ [4pt]
& & &\ quad f (x_2) =Ax_2^2+Bx_2+C\ enspace\ text {e}\ enspace f (x_0) =Ax_0^2+Bx_0+C.\\ [4pt]
&=\ frac {Δx} {3}\ big (f (x_2) +f (x_0) +A (2x_1) ^2+2B (2x_1) +4C\ big) &\ texto {Substituto}\, x_2+x_0=2x_1.\\ [4pt]
& & &\ quad\ text {Nota:}, x_1 =\ frac {x_2+x_0} {2}\ enspace\ text {é o ponto médio.}\\ [4pt]
&=\ frac {Δx} {3}\ big (f (x_2) +4f (x_1) +f (x_0)\ big). & &\ text {Expandir e substituir}\, f (x_1) =Ax_1^2+Bx_1+C.\ end {align*}\]
Se aproximarmos\(\displaystyle ∫^{x_4}_{x_2}f(x)\,dx\) usando o mesmo método, vemos que temos
\[∫^{x_4}_{x_2}f(x)\,dx≈\frac{Δx}{3}(f(x_4)+4\,f(x_3)+f(x_2)).\nonumber \]
Combinando essas duas aproximações, obtemos
\[∫^{x_4}_{x_0}f(x)\,dx≈\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+f(x_4)).\nonumber \]
O padrão continua à medida que adicionamos pares de subintervalos à nossa aproximação. A regra geral pode ser declarada da seguinte forma.
Suponha que\(f(x)\) seja um fim contínuo\([a,b]\). \(n\)Seja um número inteiro par positivo\(Δx=\dfrac{b−a}{n}\) e. Vamos\([a,b]\) ser divididos em\(n\) subintervalos, cada um de comprimento\(Δx\), com pontos finais em\(P=\{x_0,x_1,x_2,…,x_n\}.\) Set
\[S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]. \nonumber \]
Em seguida,
\[\lim_{n→+∞}S_n=∫^b_af(x)\,dx.\nonumber \]
Assim como a regra trapezoidal é a média das regras da mão esquerda e da direita para estimar integrais definidas, a regra de Simpson pode ser obtida a partir do ponto médio e das regras trapezoidais usando uma média ponderada. Pode-se mostrar que\(S_{2n}=\left(\frac{2}{3}\right)M_n+\left(\frac{1}{3}\right)T_n\).
Também é possível limitar o erro ao usar a regra de Simpson para aproximar uma integral definida. O limite do erro é dado pela seguinte regra:
\(f(x)\)Seja uma função contínua sobre\([a,b]\) ter uma quarta derivada\( f^{(4)}(x)\),, nesse intervalo. Se\(M\) for o valor máximo de\(∣f^{(4)}(x)∣\) mais\([a,b]\), então o limite superior para o erro de uso\(S_n\) para estimar\(\displaystyle ∫^b_af(x)\,dx\) é dado por
\[\text{Error in}\, S_n≤\frac{M(b−a)^5}{180n^4}. \nonumber \]
Use\(S_2\) para aproximar\(\displaystyle ∫^1_0x^3\,dx\). Estime um limite para o erro em\(S_2\).
Solução
Como\([0,1]\) é dividido em dois intervalos, cada subintervalo tem comprimento\(Δx=\frac{1−0}{2}=\frac{1}{2}\). Os pontos finais desses subintervalos são\(\left\{0,\frac{1}{2},1\right\}\). Se definirmos\(f(x)=x^3,\) então
\[S_2=\frac{1}{3}⋅\frac{1}{2}(f(0)+4\,f(\frac{1}{2})+f(1))=\frac{1}{6}(0+4⋅\frac{1}{8}+1)=\frac{1}{4}.\nonumber \]
Desde então,\( f^{(4)}(x)=0\) e consequentemente,\(M=0,\) vemos que
Erro em\(S_2≤\frac{0(1)^5}{180⋅2^4}=0.\)
Esse limite indica que o valor obtido por meio da regra de Simpson é exato. Uma verificação rápida verificará se, de fato,\(\displaystyle ∫^1_0x^3\,dx=\frac{1}{4}.\)
Use\(S_6\) para estimar o comprimento da curva\(y=\frac{1}{2}x^2\) acima\([1,4].\)
Solução
O comprimento do\(y=\frac{1}{2}x^2\) over\([1,4]\) é\(\displaystyle ∫^4_1\sqrt{1+x^2}\,dx\). Se\([1,4]\) dividirmos em seis subintervalos, então cada subintervalo tem comprimento\(Δx=\frac{4−1}{6}=\frac{1}{2}\) e os pontos finais dos subintervalos são\( \left\{1,\frac{3}{2},2,\frac{5}{2},3,\frac{7}{2},4\right\}.\) Setting\( f(x)=\sqrt{1+x^2}\),
\[S_6=\frac{1}{3}⋅\frac{1}{2}(f(1)+4f(\frac{3}{2})+2f(2)+4f(\frac{5}{2})+2f(3)+4f(\frac{7}{2})+f(4)).\nonumber \]
Depois de substituir, temos
\[S_6=\frac{1}{6}(1.4142+4⋅1.80278+2⋅2.23607+4⋅2.69258+2⋅3.16228+4⋅3.64005+4.12311)≈8.14594\,\text{units}. \nonumber \]
Use\(S_2\) para estimar\(\displaystyle ∫^2_1\frac{1}{x}\,dx.\)
- Dica
-
\[S_2=\frac{1}{3}Δx\left(f(x_0)+4f(x_1)+f(x_2)\right) \nonumber \]
- Resposta
-
\(\frac{25}{36} \approx 0.694444\)
Conceitos-chave
- Podemos usar a integração numérica para estimar os valores de integrais definidas quando uma forma fechada da integral é difícil de encontrar ou quando um valor aproximado somente da integral definida é necessário.
- As técnicas mais usadas para integração numérica são a regra do ponto médio, a regra trapezoidal e a regra de Simpson.
- A regra do ponto médio se aproxima da integral definida usando regiões retangulares, enquanto a regra trapezoidal se aproxima da integral definida usando aproximações trapezoidais.
- A regra de Simpson se aproxima da integral definida aproximando primeiro a função original usando funções quadráticas por partes.
Equações-chave
- Regra do ponto médio
\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\)
- Regra trapezoidal
\(T_n=\frac{Δx}{2}\Big[f(x_0)+2\,f(x_1)+2\,f(x_2)+⋯+2\,f(x_{n−1})+f(x_n)\Big]\)
- A regra de Simpson
\(S_n=\frac{Δx}{3}\Big[f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+4\,f(x_5)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\Big]\)
- Erro vinculado à regra do ponto médio
Erro em\(M_n≤\dfrac{M(b−a)^3}{24n^2}\), onde\(M\) é o valor máximo de\(|f''(x)|\) over\([a,b]\).
- Limite de erro para regra trapezoidal
Erro em\(T_n≤\dfrac{M(b−a)^3}{12n^2}\), onde\(M\) é o valor máximo de\(|f''(x)|\) over\([a,b]\).
- Erro associado à regra de Simpson
Erro em\(S_n≤\dfrac{M(b−a)^5}{180n^4}\), onde\(M\) é o valor máximo de\(∣f^{(4)}(x)∣\) over\([a,b]\).
Glossário
- erro absoluto
- se\(B\) for uma estimativa de alguma quantidade com um valor real de\(A\), então o erro absoluto é dado por\( |A−B|\)
- regra do ponto médio
- uma regra que usa uma soma de Riemann da forma\(\displaystyle M_n=\sum^n_{i=1}f(m_i)Δx\), onde\( m_i\) é o ponto médio do\(i^{\text{th}}\) subintervalo a ser aproximado\(\displaystyle ∫^b_af(x)\,dx\)
- integração numérica
- a variedade de métodos numéricos usados para estimar o valor de uma integral definida, incluindo a regra do ponto médio, a regra trapezoidal e a regra de Simpson
- erro relativo
- erro como uma porcentagem do valor real, dado por\[\text{relative error}=\left|\frac{A−B}{A}\right|⋅100\%\nonumber \]
- A regra de Simpson
- uma regra que se aproxima\(\displaystyle ∫^b_af(x)\,dx\) usando a área sob uma função quadrática por partes.
A aproximação\(S_n\) de\(\displaystyle ∫^b_af(x)\,dx\) é dada por\[S_n=\frac{Δx}{3}\big(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f(x_3)+2\,f(x_4)+⋯+2\,f(x_{n−2})+4\,f(x_{n−1})+f(x_n)\big).\nonumber \]
- regra trapezoidal
- uma regra que se aproxima do\(\displaystyle ∫^b_af(x)\,dx\) uso da área dos trapézios.
A aproximação\(T_n\) de\(\displaystyle ∫^b_af(x)\,dx\) é dada por\[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_{n−1})+f(x_n)\big).\nonumber \]
Contribuidores e atribuições
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger (Monroe Community College). Notes added to development of area under a parabola and typos fixed in original text.


