6.8: Crescimento e decadência exponenciais
- Page ID
- 187856
- Use o modelo de crescimento exponencial em aplicações, incluindo crescimento populacional e juros compostos.
- Explique o conceito de duplicação do tempo.
- Use o modelo de decaimento exponencial em aplicações, incluindo decaimento radioativo e a lei de resfriamento de Newton.
- Explique o conceito de meia-vida.
Uma das aplicações mais comuns das funções exponenciais envolve modelos de crescimento e decaimento. O crescimento e a decadência exponenciais aparecem em uma série de aplicações naturais. Do crescimento populacional e do interesse contínuo agravado ao decaimento radioativo e à lei de resfriamento de Newton, as funções exponenciais são onipresentes na natureza. Nesta seção, examinamos o crescimento e a decadência exponenciais no contexto de algumas dessas aplicações.
Modelo de crescimento exponencial
Muitos sistemas apresentam crescimento exponencial. Esses sistemas seguem um modelo da forma\(y=y_0e^{kt},\) em que\(y_0\) representa o estado inicial do sistema e\(k\) é uma constante positiva, chamada de constante de crescimento. Observe que em um modelo de crescimento exponencial, temos
\[ y′=ky_0e^{kt}=ky. \label{eq1} \]
Ou seja, a taxa de crescimento é proporcional ao valor atual da função. Essa é uma característica fundamental do crescimento exponencial. A equação\ ref {eq1} envolve derivadas e é chamada de equação diferencial.
Sistemas que apresentam crescimento exponencial aumentam de acordo com o modelo matemático
\[y=y_0e^{kt} \nonumber \]
onde\(y_0\) representa o estado inicial do sistema e\(k>0\) é uma constante, chamada de constante de crescimento.
O crescimento populacional é um exemplo comum de crescimento exponencial. Considere uma população de bactérias, por exemplo. Parece plausível que a taxa de crescimento populacional seja proporcional ao tamanho da população. Afinal, quanto mais bactérias houver para se reproduzir, mais rápido a população cresce. A Figura\(\PageIndex{1}\) e a Tabela\(\PageIndex{1}\) representam o crescimento de uma população de bactérias com uma população inicial de 200 bactérias e uma constante de crescimento de 0,02. Observe que depois de apenas 2 horas (120 minutos), a população tem 10 vezes o tamanho original!
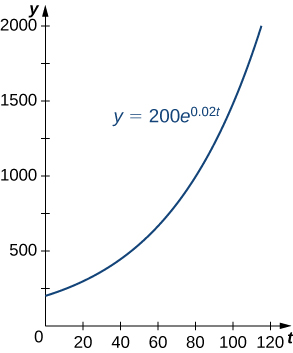
| Tempo (min) | Tamanho da população (número de bactérias) |
|---|---|
| 10 | 244 |
| 20 | 298 |
| 30 | 364 |
| 40 | 445 |
| 50 | 544 |
| 60 | 664 |
| 70 | 811 |
| 80 | 991 |
| 90 | 1210 |
| 100 | 1478 |
| 110 | 1805 |
| 120 | 2205 |
Observe que estamos usando uma função contínua para modelar o que é um comportamento inerentemente discreto. A qualquer momento, a população do mundo real contém um número inteiro de bactérias, embora o modelo assuma valores não inteiros. Ao usar modelos de crescimento exponencial, devemos sempre ter o cuidado de interpretar os valores da função no contexto do fenômeno que estamos modelando.
Considere a população de bactérias descrita anteriormente. Essa população cresce de acordo com a função em\(f(t)=200e^{0.02t},\) que t é medido em minutos. Quantas bactérias estão presentes na população após\(5\) horas (\(300\)minutos)? Quando a população atinge\(100,000\) as bactérias?
Solução
Nós temos\(f(t)=200e^{0.02t}.\) então
\[ f(300)=200e^{0.02(300)}≈80,686. \nonumber \]
Há\(80,686\) bactérias na população após o\(5\) expediente.
Para descobrir quando a população atinge\(100,000\) bactérias, resolvemos a equação
\[ \begin{align*} 100,000 &= 200e^{0.02t} \\[4pt] 500 &=e^{0.02t} \\[4pt] \ln 500 &=0.02 t \\[4pt] t &=\frac{\ln 500}{0.02}≈310.73. \end{align*} \nonumber \]
A população atinge\(100,000\) as bactérias após\(310.73\) alguns minutos.
Considere uma população de bactérias que cresce de acordo com a função\(f(t)=500e^{0.05t}\), onde\(t\) é medida em minutos. Quantas bactérias estão presentes na população após 4 horas? Quando a população atinge\(100\) milhões de bactérias?
- Resposta
-
Use o processo do exemplo anterior.
- Resposta
-
Há\(81,377,396\) bactérias na população após o\(4\) expediente. A população atinge\(100\) milhões de bactérias após\(244.12\) minutos.
Vamos agora voltar nossa atenção para uma aplicação financeira: juros compostos. Os juros que não são compostos são chamados de juros simples. Os juros simples são pagos uma vez, no final do período especificado (geralmente\(1\) ano). Então, se colocarmos\($1000\) em uma conta poupança ganhando juros\(2%\) simples por ano, então, no final do ano, temos
\[ 1000(1+0.02)=$1020. \nonumber \]
Os juros compostos são pagos várias vezes por ano, dependendo do período de composição. Portanto, se o banco acumular os juros a cada\(6\) mês, ele credita metade dos juros do ano na conta após\(6\) meses. Durante o segundo semestre do ano, a conta gera juros não apenas sobre a inicial\($1000\), mas também sobre os juros auferidos durante o primeiro semestre do ano. Matematicamente falando, no final do ano, temos
\[ 1000 \left(1+\dfrac{0.02}{2}\right)^2=$1020.10. \nonumber \]
Da mesma forma, se os juros forem aumentados a cada\(4\) mês, temos
\[ 1000 \left(1+\dfrac{0.02}{3}\right)^3=$1020.13, \nonumber \]
e se os juros forem compostos diariamente (\(365\)vezes por ano), temos\($1020.20\). Se estendermos esse conceito, para que os juros sejam compostos continuamente, depois de\(t\) anos temos
\[ 1000\lim_{n→∞} \left(1+\dfrac{0.02}{n}\right)^{nt}. \nonumber \]
Agora vamos manipular essa expressão para que tenhamos uma função de crescimento exponencial. Lembre-se de que o número\(e\) pode ser expresso como um limite:
\[ e=\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m. \nonumber \]
Com base nisso, queremos que a expressão dentro dos parênteses tenha a forma\((1+1/m)\). Deixe\(n=0.02m\). Observe isso\(n→∞, m→∞\) também. Em seguida, obtemos
\[ 1000\lim_{n→∞}\left(1+\dfrac{0.02}{n}\right)^{nt}=1000\lim_{m→∞}\left(1+\dfrac{0.02}{0.02m}\right)^{0.02mt}=1000\left[\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m\right]^{0.02t}. \nonumber \]
Reconhecemos o limite dentro dos colchetes como o número\(e\). Portanto, o saldo em nossa conta bancária após\(t\) anos é dado por\(1000 e^{0.02t}\). Generalizando esse conceito, vemos que se uma conta bancária com um saldo inicial de\($P\) ganha juros a uma taxa de\(r%\), composta continuamente, então o saldo da conta após\(t\) anos é
\[ \text{Balance}\;=Pe^{rt}. \nonumber \]
Um estudante de 25 anos tem a oportunidade de investir algum dinheiro em uma conta de aposentadoria que paga juros\(5%\) anuais compostos continuamente. Quanto a estudante precisa investir hoje para ter um\($1\) milhão quando se aposentar com a idade\(65\)? E se ela pudesse ganhar juros\(6%\) anuais compostos continuamente?
Solução
Nós temos
\[ 1,000,000=Pe^{0.05(40)} \nonumber \]
\[ P=135,335.28. \nonumber \]
Ela deve investir\($135,335.28\) com\(5%\) juros.
Se, em vez disso, ela for capaz de ganhar\(6%,\), a equação se torna
\[ 1,000,000=Pe^{0.06(40)} \nonumber \]
\[ P=90,717.95. \nonumber \]
Nesse caso, ela precisa investir apenas.\($90,717.95.\) Isso é cerca de dois terços do valor em que ela precisa investir\(5%\). O fato de os juros serem compostos continuamente amplia muito o efeito do\(1%\) aumento da taxa de juros.
Suponha que, em vez de investir na idade\(25\sqrt{b^2−4ac}\), o aluno espere até a idade\(35\). Em quanto ela teria que investir\(5%\)? Em\(6%\)?
- Dica
-
Use o processo do exemplo anterior.
- Resposta
-
Com\(5%\) juros, ela deve investir\($223,130.16\). Com\(6%\) juros, ela deve investir\($165,298.89.\)
Se uma quantidade crescer exponencialmente, o tempo necessário para que a quantidade dobre permanece constante. Em outras palavras, leva a mesma quantidade de tempo para que uma população de bactérias cresça\(100\) a partir de uma\(200\) bactéria e para uma\(20,000\) bactéria.\(10,000\) Esse tempo é chamado de tempo de duplicação. Para calcular o tempo de duplicação, queremos saber quando a quantidade atinge o dobro do tamanho original. Então, nós temos
\[ \begin{align*} 2y_0 &=y_0e^{kt} \\[4pt] 2 &=e^{kt} \\[4pt] \ln 2 &=kt \\[4pt] t &=\dfrac{\ln 2}{k}. \end{align*} \nonumber \]
Se uma quantidade cresce exponencialmente, o tempo de duplicação é a quantidade de tempo que a quantidade leva para dobrar. É dado por
\[\text{Doubling time}=\dfrac{\ln 2}{k}. \nonumber \]
Suponha que uma população de peixes cresça exponencialmente. Um lago é abastecido inicialmente com\(500\) peixes. Depois de\(6\) meses, há\(1000\) peixes na lagoa. O proprietário permitirá que seus amigos e vizinhos pesquem em seu lago depois que a população de peixes chegar\(10,000\). Quando os amigos do proprietário poderão pescar?
Solução
Sabemos que a população de peixes leva\(6\) meses para dobrar de tamanho. Então, se\(t\) representa o tempo em meses, pela fórmula do tempo de duplicação, nós temos\(6=(\ln 2)/k\). Então,\(k=(\ln 2)/6\). Assim, a população é dada por\(y=500e^{((\ln 2)/6)t}\). Para descobrir quando a população chega aos\(10,000\) peixes, devemos resolver a seguinte equação:
\[ \begin{align*} 10,000 &=500e^{(\ln 2/6)t} \\[4pt] 20 &=e^{(\ln 2/6)t} \\[4pt] \ln 20 &=\left(\frac{\ln 2}{6}\right)t \\[4pt] t &=\frac{6(\ln 20)}{\ln 2} \\[4pt] &≈25.93. \end{align*} \nonumber \]
Os amigos do proprietário precisam esperar\(25.93\) meses (pouco mais de\(2\) anos) para pescar na lagoa.
Suponha que a população de peixes em Example leve\(9\) meses\(\PageIndex{3}\) para alcançar\(1000\) peixes. Nessas circunstâncias, quanto tempo os amigos do proprietário precisam esperar?
- Dica
-
Use o processo do exemplo anterior.
- Resposta
-
\(38.90\)meses
Modelo de decaimento exponencial
As funções exponenciais também podem ser usadas para modelar populações que encolhem (devido a doenças, por exemplo) ou compostos químicos que se decompõem com o tempo. Dizemos que esses sistemas exibem decaimento exponencial, em vez de crescimento exponencial. O modelo é quase o mesmo, exceto que há um sinal negativo no expoente. Assim, para alguma constante positiva\(k\), temos
\[ y=y_0e^{−kt}. \nonumber \]
Tal como acontece com o crescimento exponencial, há uma equação diferencial associada ao decaimento exponencial. Nós temos
\[ y′=−ky_0e^{−kt}=−ky. \nonumber \]
Sistemas que exibem decaimento exponencial se comportam de acordo com o modelo
\[y=y_0e^{−kt}, \nonumber \]
onde\(y_0\) representa o estado inicial do sistema e\(k>0\) é uma constante, chamada de constante de decaimento.
A figura\(\PageIndex{2}\) mostra um gráfico de uma função representativa de decaimento exponencial.
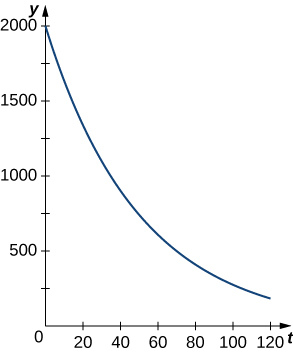
Vejamos uma aplicação física do decaimento exponencial. A lei de resfriamento de Newton diz que um objeto esfria a uma taxa proporcional à diferença entre a temperatura do objeto e a temperatura do ambiente. Em outras palavras, se\(T\) representa a temperatura do objeto e\(T_a\) representa a temperatura ambiente em uma sala, então
\[T′=−k(T−T_a). \nonumber \]
Observe que esse não é o modelo certo para decaimento exponencial. Queremos que a derivada seja proporcional à função, e essa expressão tem o\(T_a\) termo adicional. Felizmente, podemos fazer uma mudança de variáveis que resolva esse problema. Deixe\(y(t)=T(t)−T_a\). Então\(y′(t)=T′(t)−0=T′(t)\), e nossa equação se torna
\[ y′=−ky. \nonumber \]
De nosso trabalho anterior, sabemos que essa relação entre\(y\) e sua derivada leva à decadência exponencial. Assim,
\[ y=y_0e^{−kt}, \nonumber \]
e vemos que
\[ T−T_a=(T_0−T_a)e^{−kt} \nonumber \]
\[ T=(T_0−T_a)e^{−kt}+T_a \nonumber \]
onde\(T_0\) representa a temperatura inicial. Vamos aplicar essa fórmula no exemplo a seguir.
De acordo com baristas experientes, a temperatura ideal para servir café é entre\(155°F\)\(175°F\) e. Suponha que o café seja servido a uma temperatura de e\(200°F\), após\(2\) alguns minutos, em uma\(70°F\) sala, ele tenha esfriado\(180°F\). Quando o café é frio o suficiente para servir pela primeira vez? Quando o café está muito frio para servir? Arredonde as respostas para o meio minuto mais próximo.
Solução
Nós temos
\[ \begin{align*} T &=(T_0−T_a)e^{−kt}+T_a \\[4pt] 180 &=(200−70)e^{−k(2)}+70 \\[4pt] 110 &=130e^{−2k} \\[4pt] \dfrac{11}{13} &=e^{−2k} \\[4pt] \ln \dfrac{11}{13} &=−2k \\[4pt] \ln 11−\ln 13 &=−2k \\[4pt] k &=\dfrac{\ln 13−\ln 11}{2} \end{align*}\]
Então, o modelo é
\[T=130e^{(\ln 11−\ln 13/2)t}+70. \nonumber \]
O café chega\(175°F\) quando
\[ \begin{align*} 175 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt]105 &=130e^{(\ln 11−\ln 13/2)t} \\[4pt] \dfrac{21}{26} &=e^{(\ln 11−\ln 13/2)t} \\[4pt] \ln \dfrac{21}{26} &=\dfrac{\ln 11−\ln 13}{2}t \\[4pt] \ln 21−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 21−\ln 26)}{\ln 11−\ln 13}\\[4pt] &≈2.56. \end{align*}\]
O café pode ser servido cerca de\(2.5\) minutos após ser servido. O café chega\(155°F\) a
\[ \begin{align*} 155 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt] 85 &=130e^{(\ln 11−\ln 13)t} \\[4pt] \dfrac{17}{26} &=e^{(\ln 11−\ln 13)t} \\[4pt] \ln 17−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 17−\ln 26)}{\ln 11−\ln 13} \\[4pt] &≈5.09.\end{align*}\]
O café está muito frio para ser servido cerca de\(5\) minutos depois de ser servido.
Suponha que a sala esteja mais quente\((75°F)\) e, depois de\(2\) minutos, o café tenha esfriado apenas até\(185°F.\) Quando o café é frio o suficiente para servir? Quando o café fica muito frio para servir? Arredonde as respostas para o meio minuto mais próximo.
- Dica
-
Use o processo do exemplo anterior.
- Resposta
-
O café é primeiro frio o suficiente para servir cerca de\(3.5\) minutos depois de ser servido. O café está muito frio para servir cerca de\(7\) minutos depois de ser servido.
Assim como os sistemas que exibem crescimento exponencial têm um tempo de duplicação constante, os sistemas que exibem decaimento exponencial têm uma meia-vida constante. Para calcular a meia-vida, queremos saber quando a quantidade atinge a metade do tamanho original. Portanto, temos
\(\dfrac{y_0}{2}=y_0e^{−kt}\)
\(\dfrac{1}{2}=e^{−kt}\)
\(−\ln 2=−kt\)
\(t=\dfrac{\ln 2}{k}\).
Nota: Essa é a mesma expressão que criamos para duplicar o tempo.
Se uma quantidade decair exponencialmente, a meia-vida é a quantidade de tempo que a quantidade leva para ser reduzida pela metade. É dado por
\[\text{Half-life}=\dfrac{\ln 2}{k}. \nonumber \]
Uma das aplicações mais comuns de um modelo de decaimento exponencial é a datação por carbono. O carbono-14 decai (emite uma partícula radioativa) a uma taxa exponencial regular e consistente. Portanto, se soubermos quanto carbono-14 estava originalmente presente em um objeto e quanto carbono 14 permanece, podemos determinar a idade do objeto. A meia-vida do carbono-14 é de aproximadamente 5730 anos, o que significa que, após tantos anos, metade do material foi convertido do carbono-14 original para o novo nitrogênio-14 não radioativo. Se tivermos 100 g de carbono-14 hoje, quanto resta em 50 anos? Se um artefato que originalmente continha 100 g de carbono-14 agora contém 10 g de carbono-14, quantos anos tem? Arredonde a resposta para os cem anos mais próximos.
Solução
Nós temos
\[ 5730=\dfrac{\ln 2}{k} \nonumber \]
\[ k=\dfrac{\ln 2}{5730}.\nonumber \]
Então, o modelo diz
\[ y=100e^{−(\ln 2/5730)t}.\nonumber \]
Em\(50\) anos, temos
\[y=100e^{−(\ln 2/5730)(50)}≈99.40\nonumber \]
Portanto, em\(50\) anos, restam\(99.40\) g de carbono-14.
Para determinar a idade do artefato, devemos resolver
\[ \begin{align*} 10 &=100e^{−(\ln 2/5730)t} \\[4pt] \dfrac{1}{10} &= e^{−(\ln 2/5730)t} \\ t &≈19035. \end{align*}\]
O artefato tem cerca de\(19,000\) anos.
Se tivermos 100 g de carbono-14 , quanto resta depois de 500 anos? Se um artefato que originalmente continha 100 g de carbono-14 agora contém 20 g de carbono-14, quantos anos tem? Arredonde a resposta para os cem anos mais próximos.
- Dica
-
Use o processo do exemplo anterior.
- Resposta
-
Um total de 94,13 g de carbono-14 permanecem após 500 anos. O artefato tem aproximadamente 13.300 anos.
Conceitos chave
- O crescimento exponencial e o decaimento exponencial são duas das aplicações mais comuns das funções exponenciais.
- Os sistemas que apresentam crescimento exponencial seguem um modelo da forma\(y=y_0e^{kt}\).
- No crescimento exponencial, a taxa de crescimento é proporcional à quantidade presente. Em outras palavras,\(y′=ky\).
- Sistemas que apresentam crescimento exponencial têm um tempo de duplicação constante, que é dado por\((\ln 2)/k\).
- Sistemas que exibem decaimento exponencial seguem um modelo da forma\(y=y_0e^{−kt}.\)
- Sistemas que exibem decaimento exponencial têm uma meia-vida constante, que é dada por\((\ln 2)/k.\)
Glossário
- tempo de duplicação
- se uma quantidade cresce exponencialmente, o tempo de duplicação é a quantidade de tempo que a quantidade leva para dobrar e é dado por\((\ln 2)/k\)
- decaimento exponencial
- sistemas que exibem decaimento exponencial seguem um modelo da forma\(y=y_0e^{−kt}\)
- crescimento exponencial
- sistemas que apresentam crescimento exponencial seguem um modelo da forma\(y=y_0e^{kt}\)
- meia-vida
- se uma quantidade decai exponencialmente, a meia-vida é a quantidade de tempo que a quantidade leva para ser reduzida pela metade. É dado por\((\ln 2)/k\)


