6.4: Comprimento do arco de uma curva e área de superfície
- Page ID
- 187867
- Determine o comprimento de uma curva,\(y=f(x)\), entre dois pontos.
- Determine o comprimento de uma curva,\(x=g(y)\), entre dois pontos.
- Encontre a área da superfície de um sólido de revolução.
Nesta seção, usamos integrais definidas para determinar o comprimento do arco de uma curva. Podemos pensar no comprimento do arco como a distância que você percorreria se estivesse caminhando ao longo do caminho da curva. Muitas aplicações do mundo real envolvem o comprimento do arco. Se um foguete for lançado ao longo de um caminho parabólico, talvez queiramos saber até onde o foguete viaja. Ou, se uma curva em um mapa representa uma estrada, talvez queiramos saber até onde devemos dirigir para chegar ao nosso destino.
Começamos calculando o comprimento do arco das curvas definidas como funções de e\( x\), em seguida, examinamos o mesmo processo para curvas definidas como funções de\( y\). (O processo é idêntico, com as funções de\( x\) e\( y\) invertido.) As técnicas que usamos para encontrar o comprimento do arco podem ser estendidas para encontrar a área da superfície de uma superfície de revolução, e fechamos a seção com um exame desse conceito.
Comprimento do arco da curva y = f (x)
Em aplicações anteriores de integração, precisávamos que\( f(x)\) a função fosse integrável ou, no máximo, contínua. No entanto, para calcular o comprimento do arco, temos um requisito mais rigoroso para\( f(x)\). Aqui, precisamos\( f(x)\) ser diferenciáveis e, além disso,\( f′(x),\) exigimos que sua derivada seja contínua. Funções como essa, que têm derivadas contínuas, são chamadas de suaves. (Essa propriedade aparece novamente em capítulos posteriores.)
\( f(x)\)Seja uma função suave definida acima\( [a,b]\). Queremos calcular o comprimento da curva do ponto\( (a,f(a))\) ao ponto\( (b,f(b))\). Começamos usando segmentos de linha para aproximar o comprimento da curva. Para\( i=0,1,2,…,n\),\( P={x_i}\) seja uma partição regular de\( [a,b]\). Em seguida\( i=1,2,…,n\), para, construa um segmento de linha do ponto\( (x_{i−1},f(x_{i−1}))\) ao ponto\( (x_i,f(x_i))\). Embora possa parecer lógico usar segmentos de linha horizontais ou verticais, queremos que nossos segmentos de linha se aproximem da curva o mais próximo possível. A\(\PageIndex{1}\) figura mostra essa construção para\( n=5\).
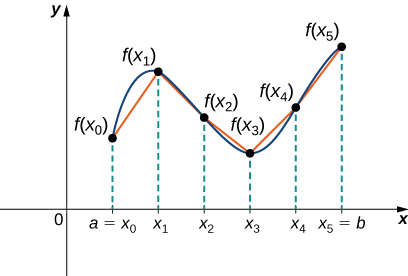
Para nos ajudar a encontrar o comprimento de cada segmento de linha, observamos a mudança na distância vertical, bem como a mudança na distância horizontal em cada intervalo. Como usamos uma partição regular, a mudança na distância horizontal em cada intervalo é dada por\( Δx\). No entanto, a mudança na distância vertical varia de intervalo para intervalo, então usamos\( Δy_i=f(x_i)−f(x_{i−1})\) para representar a mudança na distância vertical ao longo do intervalo\( [x_{i−1},x_i]\), conforme mostrado na Figura\(\PageIndex{2}\). Observe que alguns (ou todos)\( Δy_i\) podem ser negativos.
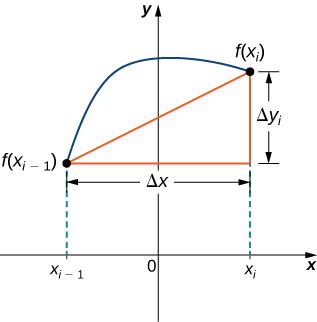
Pelo teorema de Pitágoras, o comprimento do segmento de reta é
\[ \sqrt{(Δx)^2+(Δy_i)^2}. \nonumber \]
Também podemos escrever isso como
\[ Δx\sqrt{1+((Δy_i)/(Δx))^2}. \nonumber \]
Agora, pelo Teorema do Valor Médio, há um ponto\( x^∗_i∈[x_{i−1},x_i]\) como esse\( f′(x^∗_i)=(Δy_i)/(Δx)\). Em seguida, o comprimento do segmento de linha é dado por
\[ Δx\sqrt{1+[f′(x^∗_i)]^2}. \nonumber \]
Somando os comprimentos de todos os segmentos de linha, obtemos
\[\text{Arc Length} ≈\sum_{i=1}^n\sqrt{1+[f′(x^∗_i)]^2}Δx.\nonumber \]
Esta é uma soma de Riemann. Tomando o limite\( n→∞,\) que temos
\[\begin{align*} \text{Arc Length} &=\lim_{n→∞}\sum_{i=1}^n\sqrt{1+[f′(x^∗_i)]^2}Δx \\[4pt] &=∫^b_a\sqrt{1+[f′(x)]^2}dx.\end{align*}\]
Resumimos essas descobertas no seguinte teorema.
\( f(x)\)Seja uma função suave ao longo do intervalo\([a,b]\). Em seguida, o comprimento do arco da parte\( f(x)\) do gráfico do ponto\( (a,f(a))\) ao ponto\( (b,f(b))\) é dado por
\[\text{Arc Length}=∫^b_a\sqrt{1+[f′(x)]^2}\,dx. \nonumber \]
Observe que estamos integrando uma expressão que envolve\( f′(x)\), então precisamos ter certeza de que\( f′(x)\) é integrável. É por isso que precisamos\( f(x)\) ser suaves. O exemplo a seguir mostra como aplicar o teorema.
Deixe\( f(x)=2x^{3/2}\). Calcule o comprimento do arco do gráfico\( f(x)\) ao longo do intervalo\( [0,1]\). Arredonde a resposta para três casas decimais.
Solução
Nós temos\( f′(x)=3x^{1/2},\)\( [f′(x)]^2=9x.\) então, o comprimento do arco é
\[\begin{align*} \text{Arc Length} &=∫^b_a\sqrt{1+[f′(x)]^2}dx \nonumber \\[4pt] &= ∫^1_0\sqrt{1+9x}dx. \nonumber \end{align*}\]
Substitua\( u=1+9x.\) Então,\( du=9dx.\) Quando\( x=0\)\( u=1\), então e quando\( x=1\), então\( u=10\). Assim,
\[ \begin{align*} \text{Arc Length} &=∫^1_0\sqrt{1+9x}dx \\[4pt] =\dfrac{1}{9}∫^1_0\sqrt{1+9x}9dx \\[4pt] &= \dfrac{1}{9}∫^{10}_1\sqrt{u}du \\[4pt] &=\dfrac{1}{9}⋅\dfrac{2}{3}u^{3/2}∣^{10}_1 =\dfrac{2}{27}[10\sqrt{10}−1] \\[4pt] &≈2.268units. \end{align*}\]
Deixe\(f(x)=(4/3)x^{3/2}\). Calcule o comprimento do arco do gráfico\( f(x)\) ao longo do intervalo\( [0,1]\). Arredonde a resposta para três casas decimais.
- Dica
-
Use o processo do exemplo anterior. Não se esqueça de mudar os limites da integração.
- Responda
-
\[ \dfrac{1}{6}(5\sqrt{5}−1)≈1.697 \nonumber \]
Embora seja bom ter uma fórmula para calcular o comprimento do arco, esse teorema específico pode gerar expressões difíceis de integrar. Estudamos algumas técnicas de integração em Introdução às Técnicas de Integração. Em alguns casos, talvez precisemos usar um computador ou uma calculadora para aproximar o valor da integral.
Deixe\( f(x)=x^2\). Calcule o comprimento do arco do gráfico\( f(x)\) ao longo do intervalo\( [1,3]\).
Solução
Nós temos\( f′(x)=2x,\) isso\( [f′(x)]^2=4x^2.\) Então o comprimento do arco é dado por
\[\begin{align*} \text{Arc Length} &=∫^b_a\sqrt{1+[f′(x)]^2}\,dx \\[4pt] &=∫^3_1\sqrt{1+4x^2}\,dx. \end{align*}\]
Usando um computador para aproximar o valor dessa integral, obtemos
\[ ∫^3_1\sqrt{1+4x^2}\,dx ≈ 8.26815. \nonumber \]
Deixe\( f(x)=\sin x\). Calcule o comprimento do arco do gráfico\( f(x)\) ao longo do intervalo\( [0,π]\). Use um computador ou uma calculadora para aproximar o valor da integral.
- Dica
-
Use o processo do exemplo anterior.
- Resposta
-
\[ \text{Arc Length} ≈ 3.8202 \nonumber \]
Comprimento do arco da curva\(x = g(y)\)
Acabamos de ver como aproximar o comprimento de uma curva com segmentos de linha. Se quisermos determinar o comprimento do arco do gráfico de uma função de\(y\), podemos repetir o mesmo processo, exceto que dividimos o eixo y em vez do eixo x. A figura\(\PageIndex{3}\) mostra um segmento de linha representativo.
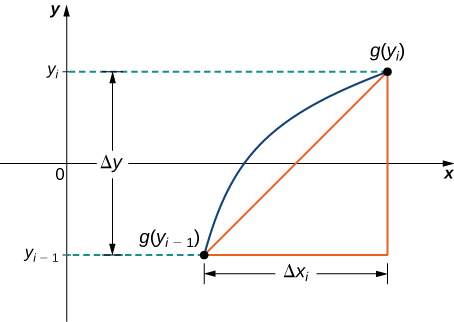
Então, o comprimento do segmento de linha é
\[\sqrt{(Δy)^2+(Δx_i)^2}, \nonumber \]
que também pode ser escrito como
\[Δy\sqrt{1+\left(\dfrac{Δx_i}{Δy}\right)^2}. \nonumber \]
Se agora seguirmos o mesmo desenvolvimento que fizemos anteriormente, obteremos uma fórmula para o comprimento do arco de uma função\(x=g(y)\).
\(g(y)\)Seja uma função suave em um intervalo\([c,d]\). Então, o comprimento do arco do gráfico\(g(y)\) do ponto\((c,g(c))\) ao ponto\((d,g(d))\) é dado por
\[\text{Arc Length}=∫^d_c\sqrt{1+[g′(y)]^2}dy. \nonumber \]
Vamos\(g(y)=3y^3.\) calcular o comprimento do arco do gráfico\(g(y)\) ao longo do intervalo\([1,2]\).
Solução
Nós temos\(g′(y)=9y^2,\) então\([g′(y)]^2=81y^4.\) então o comprimento do arco é
\[\begin{align*} \text{Arc Length} &=∫^d_c\sqrt{1+[g′(y)]^2}dy \\[4pt] &=∫^2_1\sqrt{1+81y^4}dy.\end{align*}\]
Usando um computador para aproximar o valor dessa integral, obtemos
\[ ∫^2_1\sqrt{1+81y^4}dy≈21.0277.\nonumber \]
Deixe\(g(y)=1/y\). Calcule o comprimento do arco do gráfico\(g(y)\) ao longo do intervalo\([1,4]\). Use um computador ou uma calculadora para aproximar o valor da integral.
- Dica
-
Use o processo do exemplo anterior.
- Resposta
-
\[\text{Arc Length} =3.15018 \nonumber \]
Área de uma superfície de revolução
Os conceitos que usamos para determinar o comprimento do arco de uma curva podem ser estendidos para encontrar a área da superfície de uma superfície de revolução. A área da superfície é a área total da camada externa de um objeto. Para objetos como cubos ou tijolos, a área da superfície do objeto é a soma das áreas de todas as suas faces. Para superfícies curvas, a situação é um pouco mais complexa. \(f(x)\)Seja uma função suave não negativa ao longo do intervalo\([a,b]\). Desejamos encontrar a área da superfície da revolução criada girando o gráfico\(y=f(x)\) ao redor do\(x\) eixo -, conforme mostrado na figura a seguir.
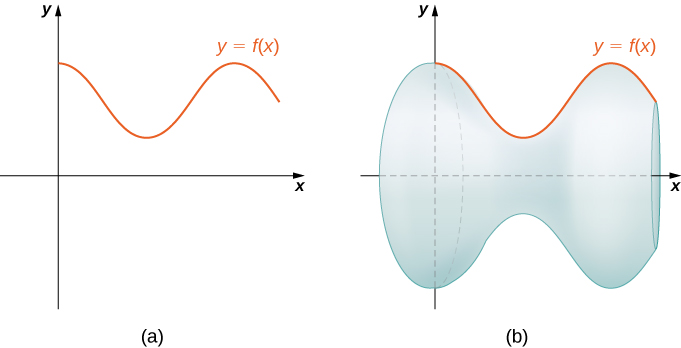
Como fizemos muitas vezes antes, vamos dividir o intervalo\([a,b]\) e aproximar a área da superfície calculando a área da superfície de formas mais simples. Começamos usando segmentos de linha para aproximar a curva, como fizemos anteriormente nesta seção. Para\(i=0,1,2,…,n\),\(P={x_i}\) seja uma partição regular de\([a,b]\). Em seguida, para\(i=1,2,…,n,\) construir um segmento de linha do ponto\((x_{i−1},f(x_{i−1}))\) ao ponto\((x_i,f(x_i))\). Agora, gire esses segmentos de linha em torno do\(x\) eixo -para gerar uma aproximação da superfície de revolução, conforme mostrado na figura a seguir.
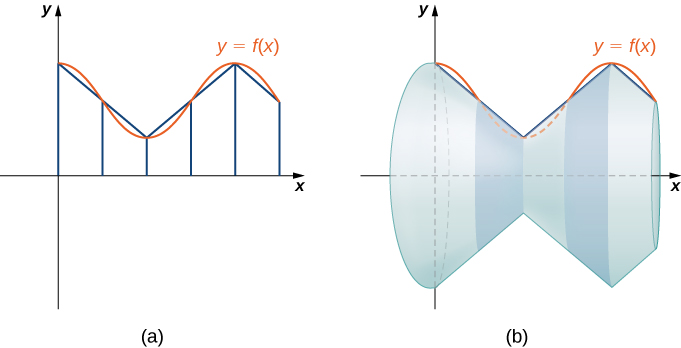
Observe que quando cada segmento de linha é girado em torno do eixo, ele produz uma faixa. Essas faixas são na verdade pedaços de cones (pense em uma casquinha de sorvete com a ponta pontiaguda cortada). Um pedaço de cone como esse é chamado de tronco de cone.
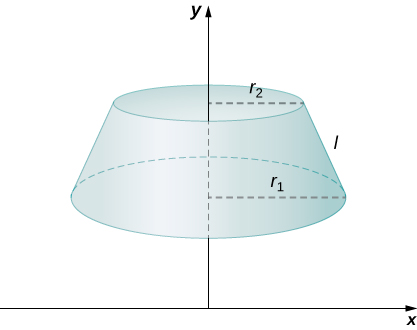
Para encontrar a área da superfície da faixa, precisamos encontrar a área da superfície lateral\(S\),, do tronco (a área apenas da superfície externa inclinada do tronco, não incluindo as áreas das faces superior ou inferior). \(r_2\)Seja\(r_1\) e seja os raios da extremidade larga e da extremidade estreita do tronco, respectivamente, e\(l\) seja a altura inclinada do tronco, conforme mostrado na figura a seguir.
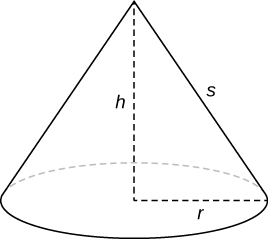
Sabemos que a área da superfície lateral de um cone é dada por
\[\text{Lateral Surface Area } =πrs, \nonumber \]
onde\(r\) está o raio da base do cone e\(s\) é a altura da inclinação (Figura\(\PageIndex{7}\)).
Como um tronco pode ser considerado um pedaço de cone, a área da superfície lateral do tronco é dada pela área da superfície lateral de todo o cone menos a área da superfície lateral do cone menor (a ponta pontiaguda) que foi cortado (Figura\(\PageIndex{8}\)).
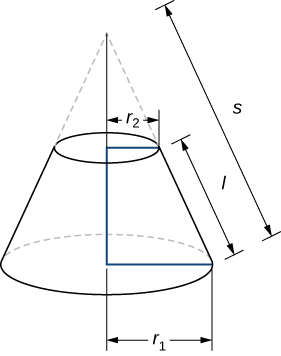
As seções transversais do cone pequeno e do cone grande são triângulos semelhantes, então vemos que
\[ \dfrac{r_2}{r_1}=\dfrac{s−l}{s} \nonumber \]
Resolvendo para\(s\), obtemos =s−ls
\[\begin{align*} \dfrac{r_2}{r_1} &=\dfrac{s−l}{s} \\ r_2s &=r_1(s−l) \\ r_2s &=r_1s−r_1l \\ r_1l &=r_1s−r_2s \\ r_1l &=(r_1−r_2)s \\ \dfrac{r_1l}{r_1−r_2} =s \end{align*}\]
Então, a área da superfície lateral (SA) do tronco é
\[\begin{align*} S &= \text{(Lateral SA of large cone)}− \text{(Lateral SA of small cone)} \\[4pt] &=πr_1s−πr_2(s−l) \\[4pt] &=πr_1(\dfrac{r_1l}{r_1−r_2})−πr_2(\dfrac{r_1l}{r_1−r_2−l}) \\[4pt] &=\dfrac{πr^2_1l}{r^1−r^2}−\dfrac{πr_1r_2l}{r_1−r_2}+πr_2l \\[4pt] &=\dfrac{πr^2_1l}{r_1−r_2}−\dfrac{πr_1r2_l}{r_1−r_2}+\dfrac{πr_2l(r_1−r_2)}{r_1−r_2} \\[4pt] &=\dfrac{πr^2_1}{lr_1−r_2}−\dfrac{πr_1r_2l}{r_1−r_2} + \dfrac{πr_1r_2l}{r_1−r_2}−\dfrac{πr^2_2l}{r_1−r_3} \\[4pt] &=\dfrac{π(r^2_1−r^2_2)l}{r_1−r_2}=\dfrac{π(r_1−r+2)(r1+r2)l}{r_1−r_2} \\[4pt] &= π(r_1+r_2)l. \label{eq20} \end{align*} \]
Agora, vamos usar essa fórmula para calcular a área da superfície de cada uma das bandas formadas pela rotação dos segmentos de linha ao redor do\(x-axis\). Uma faixa representativa é mostrada na figura a seguir.
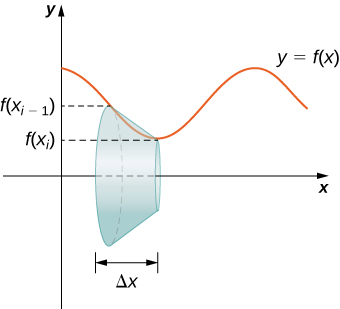
Observe que a altura inclinada desse tronco é apenas o comprimento do segmento de linha usado para gerá-lo. Então, aplicando a fórmula da área de superfície, temos
\[\begin{align*} S &=π(r_1+r_2)l \\ &=π(f(x_{i−1})+f(x_i))\sqrt{Δx^2+(Δyi)^2} \\ &=π(f(x_{i−1})+f(x_i))Δx\sqrt{1+(\dfrac{Δy_i}{Δx})^2} \end{align*}\]
Agora, como fizemos no desenvolvimento da fórmula do comprimento do arco, aplicamos o Teorema do Valor Médio para selecionar de\(x^∗_i∈[x_{i−1},x_i]\) forma que\(f′(x^∗_i)=(Δy_i)/Δx.\) Isso nos dê
\[S=π(f(x_{i−1})+f(x_i))Δx\sqrt{1+(f′(x^∗_i))^2} \nonumber \]
Além disso, como\(f(x)\) é contínuo, pelo Teorema do Valor Intermediário, há um ponto\(x^{**}_i∈[x_{i−1},x[i]\) tal que\ (f (x^ {**} _i) =( 1/2) [f (xi−1) +f (xi)],
então obtemos
\[S=2πf(x^{**}_i)Δx\sqrt{1+(f′(x^∗_i))^2}.\nonumber \]
Então, a área superficial aproximada de toda a superfície da revolução é dada por
\[\text{Surface Area} ≈\sum_{i=1}^n2πf(x^{**}_i)Δx\sqrt{1+(f′(x^∗_i))^2}.\nonumber \]
Isso quase parece uma soma de Riemann, exceto que temos funções avaliadas em dois pontos diferentes\(x^∗_i\) e\(x^{**}_{i}\), ao longo do intervalo\([x_{i−1},x_i]\). Embora não examinemos os detalhes aqui, acontece que, como\(f(x)\) é suave, se deixarmos n\(→∞\), o limite funciona da mesma forma que uma soma de Riemann, mesmo com os dois pontos de avaliação diferentes. Isso faz sentido intuitivamente. Ambos\(x^∗_i\) e x^ {**} _i\) estão no intervalo\([x_{i−1},x_i]\), então faz sentido que\(n→∞\), como, ambos\(x^∗_i\) e se\(x^{**}_i\) aproximem\(x\) Aqueles que estão interessados nos detalhes consultem um texto de cálculo avançado.
Tomando o limite à medida\(n→∞,\) que chegamos
\[ \begin{align*} \text{Surface Area} &=\lim_{n→∞}\sum_{i=1}n^2πf(x^{**}_i)Δx\sqrt{1+(f′(x^∗_i))^2} \\[4pt] &=∫^b_a(2πf(x)\sqrt{1+(f′(x))^2}) \end{align*}\]
Tal como acontece com o comprimento do arco, podemos realizar um desenvolvimento semelhante para funções de\(y\) obter uma fórmula para a área de superfície das superfícies de revolução em torno do\(y-axis\). Essas descobertas estão resumidas no seguinte teorema.
\(f(x)\)Seja uma função suave não negativa ao longo do intervalo\([a,b]\). Em seguida, a área da superfície da revolução formada pela rotação do gráfico\(f(x)\) em torno do eixo x é dada por
\[\text{Surface Area}=∫^b_a(2πf(x)\sqrt{1+(f′(x))^2})dx \nonumber \]
Da mesma forma,\(g(y)\) seja uma função suave não negativa ao longo do intervalo\([c,d]\). Em seguida, a área da superfície da revolução formada pela rotação do gráfico\(g(y)\) em torno do\(y-axis\) é dada por
\[\text{Surface Area}=∫^d_c(2πg(y)\sqrt{1+(g′(y))^2}dy \nonumber \]
Deixe\(f(x)=\sqrt{x}\) de lado o intervalo\([1,4]\). Encontre a área da superfície gerada girando o gráfico\(f(x)\) ao redor do\(x\) eixo -. Arredonde a resposta para três casas decimais.
Solução
O gráfico\(f(x)\) e a superfície de rotação são mostrados na Figura\(\PageIndex{10}\).
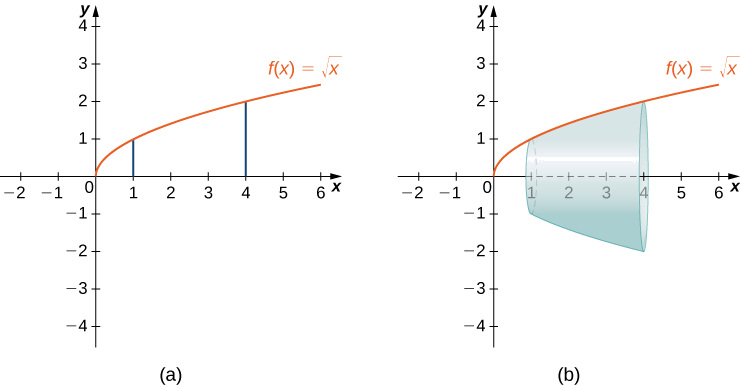
Nós temos\(f(x)=\sqrt{x}\). Então,\(f′(x)=1/(2\sqrt{x})\) e\((f′(x))^2=1/(4x).\) depois,
\[\begin{align*} \text{Surface Area} &=∫^b_a(2πf(x)\sqrt{1+(f′(x))^2}dx \\[4pt] &=∫^4_1(\sqrt{2π\sqrt{x}1+\dfrac{1}{4x}})dx \\[4pt] &=∫^4_1(2π\sqrt{x+14}dx. \end{align*}\]
Deixe\(u=x+1/4.\) então,\(du=dx\). Quando\(x=1, u=5/4\) e quando\(x=4, u=17/4.\) Isso nos dá
\[\begin{align*} ∫^1_0(2π\sqrt{x+\dfrac{1}{4}})dx &= ∫^{17/4}_{5/4}2π\sqrt{u}du \\[4pt] &= 2π\left[\dfrac{2}{3}u^{3/2}\right]∣^{17/4}_{5/4} \\[4pt] &=\dfrac{π}{6}[17\sqrt{17}−5\sqrt{5}]≈30.846 \end{align*}\]
Deixe\( f(x)=\sqrt{1−x}\) de lado o intervalo\( [0,1/2]\). Encontre a área da superfície gerada girando o gráfico\( f(x)\) ao redor do\(x\) eixo -. Arredonde a resposta para três casas decimais.
- Dica
-
Use o processo do exemplo anterior.
- Resposta
-
\[ \dfrac{π}{6}(5\sqrt{5}−3\sqrt{3})≈3.133 \nonumber \]
Deixe\( f(x)=y=\dfrac[3]{3x}\). Considere a parte da curva onde\( 0≤y≤2\). Encontre a área da superfície gerada girando o gráfico\( f(x)\) ao redor do\( y\) eixo -.
Solução
Observe que estamos girando a curva em torno do\( y\) eixo -, e o intervalo é em termos de\( y\), então queremos reescrever a função como uma função de\( y\). Nós recebemos\( x=g(y)=(1/3)y^3\). O gráfico\( g(y)\) e a superfície de rotação são mostrados na figura a seguir.
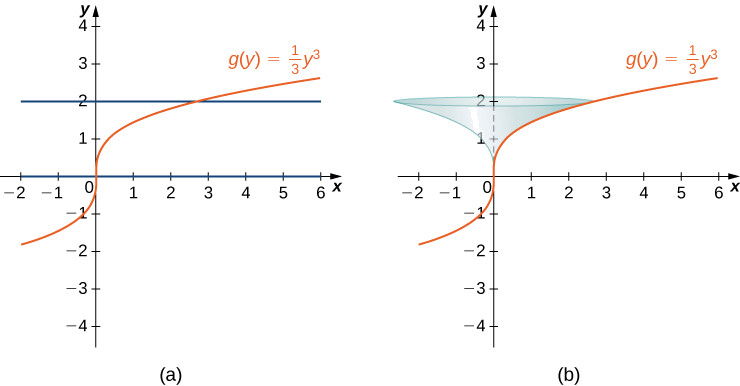
Nós temos\( g(y)=(1/3)y^3\), então\( g′(y)=y^2\)\( (g′(y))^2=y^4\) e. Então
\[\begin{align*} \text{Surface Area} &=∫^d_c(2πg(y)\sqrt{1+(g′(y))^2})dy \\[4pt] &=∫^2_0(2π(\dfrac{1}{3}y^3)\sqrt{1+y^4})dy \\[4pt] &=\dfrac{2π}{3}∫^2_0(y^3\sqrt{1+y^4})dy. \end{align*}\]
Deixe\( u=y^4+1.\) então\( du=4y^3dy\). Quando\( y=0, u=1\) e quando\( y=2, u=17.\) Então
\[\begin{align*} \dfrac{2π}{3}∫^2_0(y^3\sqrt{1+y^4})dy &=\dfrac{2π}{3}∫^{17}_1\dfrac{1}{4}\sqrt{u}du \\[4pt] &=\dfrac{π}{6}[\dfrac{2}{3}u^{3/2}]∣^{17}_1=\dfrac{π}{9}[(17)^{3/2}−1]≈24.118. \end{align*}\]
Deixe\( g(y)=\sqrt{9−y^2}\) de lado o intervalo\( y∈[0,2]\). Encontre a área da superfície gerada girando o gráfico\( g(y)\) ao redor do\( y\) eixo -.
- Dica
-
Use o processo do exemplo anterior.
- Resposta
-
\( 12π\)
Conceitos-chave
- O comprimento do arco de uma curva pode ser calculado usando uma integral definida.
- O comprimento do arco é primeiro aproximado usando segmentos de linha, o que gera uma soma de Riemann. Tomar um limite então nos dá a fórmula integral definida. O mesmo processo pode ser aplicado às funções do\( y\).
- Os conceitos usados para calcular o comprimento do arco podem ser generalizados para encontrar a área da superfície de uma superfície de revolução.
- As integrais geradas pelas fórmulas do comprimento do arco e da área da superfície geralmente são difíceis de avaliar. Pode ser necessário usar um computador ou calculadora para aproximar os valores das integrais.
Equações-chave
- Comprimento do arco de uma função de x
Comprimento do arco\( =∫^b_a\sqrt{1+[f′(x)]^2}dx\)
- Comprimento do arco de uma função de y
Comprimento do arco\( =∫^d_c\sqrt{1+[g′(y)]^2}dy\)
- Área de superfície de uma função de x
Área de superfície\( =∫^b_a(2πf(x)\sqrt{1+(f′(x))^2})dx\)
Glossário
- comprimento do arco
- o comprimento do arco de uma curva pode ser considerado como a distância que uma pessoa percorreria ao longo do caminho da curva
- tronco
- uma porção de um cone; um tronco é construído cortando o cone com um plano paralelo à base
- área de superfície
- a área da superfície de um sólido é a área total da camada externa do objeto; para objetos como cubos ou tijolos, a área da superfície do objeto é a soma das áreas de todas as suas faces


