5.7E: Exercícios para a Seção 5.7

Last updated
Save as PDF

Page ID: 187978

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Nos exercícios 1 a 6, avalie cada integral em termos de uma função trigonométrica inversa.

1)$\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}}$

Resposta: $\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}} \quad = \quad \sin^{−1}x\bigg|^{\sqrt{3}/2}_0=\dfrac{π}{3}$

2)$\displaystyle ∫^{1/2}_{−1/2}\frac{dx}{\sqrt{1−x^2}}$

3)$\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{\sqrt{1+x^2}}$

Resposta: $\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{\sqrt{1+x^2}} \quad = \quad \tan^{−1}x\bigg|^1_{\sqrt{3}}=−\dfrac{π}{12}$

4)$\displaystyle ∫^{\sqrt{3}}_{\frac{1}{\sqrt{3}}}\frac{dx}{1+x^2}$

5)$\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}}$

Resposta: $\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}} \quad = \quad \sec^{−1}x\bigg|^{\sqrt{2}}_1=\dfrac{π}{4}$

6)$\displaystyle ∫^{\frac{2}{\sqrt{3}}}_1\frac{dx}{|x|\sqrt{x^2−1}}$

Nos exercícios 7 a 12, encontre cada integral indefinida, usando as substituições apropriadas.

7)$\displaystyle ∫\frac{dx}{\sqrt{9−x^2}}$

Resposta: $\displaystyle ∫\frac{dx}{\sqrt{9−x^2}} \quad = \quad \sin^{−1}\left(\frac{x}{3}\right)+C$

8)$\displaystyle ∫\frac{dx}{\sqrt{1−16x^2}}$

9)$\displaystyle ∫\frac{dx}{9+x^2}$

Resposta: $\displaystyle ∫\frac{dx}{9+x^2} \quad = \quad \frac{1}{3}\tan^{−1}\left(\frac{x}{3}\right)+C$

10)$\displaystyle ∫\frac{dx}{25+16x^2}$

11)$\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}}$

Resposta: $\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}} \quad = \quad \frac{1}{3}\sec^{−1}\left(\frac{|x|}{3}\right)+C$

12)$\displaystyle ∫\frac{dx}{x\sqrt{4x^2−16}}$

13) Explique a relação$\displaystyle −\cos^{−1}t+C=∫\frac{dt}{\sqrt{1−t^2}}=\sin^{−1}t+C.$ É verdade, em geral, isso$\cos^{−1}t=−\sin^{−1}t$?

Resposta: $\cos(\frac{π}{2}−θ)=\sin θ.$Então,$\sin^{−1}t=\dfrac{π}{2}−\cos^{−1}t.$ eles diferem por uma constante.

14) Explique a relação$\displaystyle \sec^{−1}t+C=∫\frac{dt}{|t|\sqrt{t^2−1}}=−\csc^{−1}t+C.$ É verdade, em geral, isso$\sec^{−1}t=−\csc^{−1}t$?

15) Explique o que há de errado com a seguinte integral:$\displaystyle ∫^2_1\frac{dt}{\sqrt{1−t^2}}$.

Resposta: $\sqrt{1−t^2}$não é definido como um número real quando$t>1$.

16) Explique o que há de errado com a seguinte integral:$\displaystyle ∫^1_{−1}\frac{dt}{|t|\sqrt{t^2−1}}$.

Resposta: $\sqrt{t^2−1}$não é definido como um número real quando$-1 \lt t \lt 1$, e o integrando é indefinido quando$t = -1$ ou$t = 1$.

Nos exercícios 17 a 20, resolva a antiderivada de$f$ com e, em seguida$C=0$, use uma calculadora para representar graficamente$f$ e a antiderivada ao longo do intervalo determinado$[a,b]$. Identifique um valor$C$ tal que$C$ a adição à antiderivada recupere a integral definida$\displaystyle F(x)=∫^x_af(t)\,dt$.

17) [T]$\displaystyle ∫\frac{1}{\sqrt{9−x^2}}\,dx$ acabou$[−3,3]$

Resposta

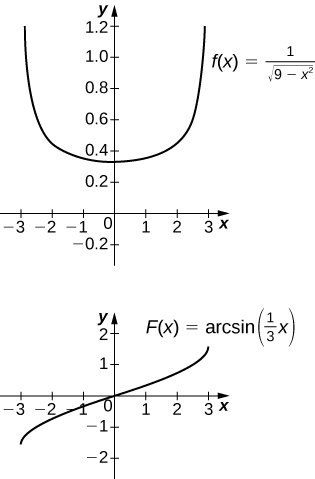
$Dois gráficos. O primeiro mostra a função f (x) = 1/sqrt (9 — x^2). É uma curva de abertura ascendente simétrica em torno do eixo y, cruzando em (0, 1/3). O segundo mostra a função F (x) = arcsin (1/3 x). É uma curva crescente passando pela origem.$

O antiderivado é$ \sin^{−1}(\frac{x}{3})+C$. A tomada$C=\frac{π}{2}$ recupera a integral definida.

18) [T]$\displaystyle ∫\frac{9}{9+x^2}\,dx$ acabou$[−6,6]$

19) [T]$\displaystyle ∫\frac{\cos x}{4+\sin^2x}\,dx$ acabou$[−6,6]$

Resposta

$Dois gráficos. O primeiro mostra a função f (x) = cos (x)/(4 + sin (x) ^2). É uma função oscilante sobre [-6, 6] com pontos de inflexão em aproximadamente (-3, -2,5), (0, .25) e (3, -2,5), onde (0, .25) é um máximo local e os outros são minutos locais. O segundo mostra a função F (x) = .5 * arctan (.5*sin (x)), que também oscila sobre [-6,6]. Tem pontos de inflexão em aproximadamente (-4,5, .25), (-1,5, -.25), (1,5, .25) e (4,5, -.25).$

O antiderivado é$\frac{1}{2}\tan^{−1}(\frac{\sin x}{2})+C$. A tomada$C=\frac{1}{2}\tan^{−1}(\frac{\sin(6)}{2})$ recupera a integral definida.

20) [T]$\displaystyle ∫\frac{e^x}{1+e^{2x}}\,dx$ acabou$[−6,6]$

Nos exercícios 21 a 26, calcule a antiderivada usando as substituições apropriadas.

21)$\displaystyle ∫\frac{\sin^{−1}t}{\sqrt{1−t^2}}\,dt$

Resposta: $\displaystyle ∫\frac{\sin^{−1}t\,dt}{\sqrt{1−t^2}} \quad = \quad \tfrac{1}{2}(\sin^{−1}t)^2+C$

22)$\displaystyle ∫\frac{dt}{\sin^{−1} t\sqrt{1−t^2}}$

23)$\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt$

Resposta: $\displaystyle ∫\frac{\tan^{−1}(2t)}{1+4t^2}\,dt \quad = \quad \frac{1}{4}(\tan^{−1}(2t))^2+C$

24)$\displaystyle ∫\frac{t\tan^{−1}(t^2)}{1+t^4}\,dt$

25)$\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt$

Resposta: $\displaystyle ∫\frac{\sec^{−1}\left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt \quad = \quad \tfrac{1}{4}(\sec^{−1}\left(\tfrac{t}{2}\right))^2+C$

26)$\displaystyle ∫\frac{t\sec^{−1}(t^2)}{t^2\sqrt{t^4−1}}\,dt$

Nos exercícios 27 a 32, use uma calculadora para representar graficamente a antiderivada de$f$ com$C=0$ ao longo do intervalo dado.$[a,b].$ Aproximadamente um valor de$C$, se possível, de modo que a adição$C$ à antiderivada forneça o mesmo valor que a integral definida$\displaystyle F(x)=∫^x_af(t)\,dt.$

27) [T]$\displaystyle ∫\frac{1}{x\sqrt{x^2−4}}\,dx$ acabou$[2,6]$

Resposta

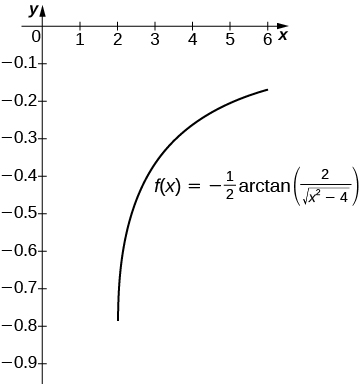
$Um gráfico da função f (x) = -.5 * arctan (2/(sqrt (x^2 — 4))) no quadrante quatro. É uma curva descendente côncava crescente com uma assíntota vertical em x=2.$

O antiderivado é$\frac{1}{2}\sec^{−1}(\frac{x}{2})+C$. A tomada$C=0$ recupera a integral definitiva$ [2,6]$.

28) [T]$\displaystyle ∫\frac{1}{(2x+2)\sqrt{x}}\,dx$ acabou$[0,6]$

29) [T]$\displaystyle ∫\frac{(\sin x+x\cos x)}{1+x^2\sin^2x\,dx}$ acabou$ [−6,6]$

Resposta

$O gráfico de f (x) = arctan (x sin (x)) sobre [-6,6]. Ele tem cinco pontos de inflexão em aproximadamente (-5, -1,5), (-2,1), (0,0), (2,1) e (5, -1,5).$

A antiderivada geral é$\tan^{−1}(x\sin x)+C$. A tomada$C=−\tan^{−1}(6\sin(6))$ recupera a integral definida.

30) [T]$\displaystyle ∫\frac{2e^{−2x}}{\sqrt{1−e^{−4x}}}\,dx$ acabou$[0,2]$

31) [T]$\displaystyle ∫\frac{1}{x+x\ln 2x}$ acabou$[0,2]$

Resposta

$Um gráfico da função f (x) = arctan (ln (x)) sobre (0, 2]. É uma curva crescente com intercepto x em (1,0).$

A antiderivada geral é$\tan^{−1}(\ln x)+C$. A tomada$\displaystyle C=\tfrac{π}{2}=\lim_{t \to ∞}\tan^{−1} t$ recupera a integral definida.

32) [T]$\displaystyle ∫\frac{\sin^{−1}x}{\sqrt{1−x^2}}$ acabou$[−1,1]$

Nos exercícios 33 a 38, calcule cada integral usando as substituições apropriadas.

33)$\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt$

Resposta: $\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt \quad = \quad \sin^{−1}(e^t)+C$

34)$\displaystyle ∫\frac{e^t}{1+e^{2t}}\,dt$

35)$\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}}$

Resposta: $\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}} \quad = \quad \sin^{−1}(\ln t)+C$

36)$\displaystyle ∫\frac{dt}{t(1+\ln^2t)}$

37)$\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt$

Resposta: $\displaystyle ∫\frac{\cos^{−1}(2t)}{\sqrt{1−4t^2}}\,dt \quad = \quad −\frac{1}{2}(\cos^{−1}(2t))^2+C$

38)$\displaystyle ∫\frac{e^t\cos^{−1}(e^t)}{\sqrt{1−e^{2t}}}\,dt$

Nos exercícios 39 a 42, calcule cada integral definida.

39)$\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt$

Resposta: $\displaystyle ∫^{1/2}_0\frac{\tan(\sin^{−1}t)}{\sqrt{1−t^2}}\,dt \quad = \quad \frac{1}{2}\ln\left(\frac{4}{3}\right)$

40)$\displaystyle ∫^{1/2}_{1/4}\frac{\tan(\cos^{−1}t)}{\sqrt{1−t^2}}\,dt$

41)$\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt$

Resposta: $\displaystyle ∫^{1/2}_0\frac{\sin(\tan^{−1}t)}{1+t^2}\,dt \quad = \quad 1−\frac{2}{\sqrt{5}}$

42)$\displaystyle ∫^{1/2}_0\frac{\cos(\tan^{−1}t)}{1+t^2}\,dt$

43) Para$A>0$,$\displaystyle I(A)=∫^{A}_{−A}\frac{dt}{1+t^2}$ compute e avalie$\displaystyle \lim_{a→∞}I(A)$, a área abaixo do gráfico de$\dfrac{1}{1+t^2}$ on$[−∞,∞]$.

Resposta: $2\tan^{−1}(A)→π$como$A→∞$

44) Para$1<B<∞$,$\displaystyle I(B)=∫^B_1\frac{dt}{t\sqrt{t^2−1}}$ compute e avalie$\displaystyle \lim_{B→∞}I(B)$, a área abaixo do gráfico de$\frac{1}{t\sqrt{t^2−1}}$ mais$[1,∞)$.

45) Use a substituição$u=\sqrt{2}\cot x$ e a identidade$1+\cot^2x=\csc^2x$ para avaliar$\displaystyle ∫\frac{dx}{1+\cos^2x}$. (Dica: multiplique a parte superior e inferior do integrando por$\csc^2x$.)

Resposta: Usando a dica, temos$\displaystyle ∫\frac{\csc^2x}{\csc^2x+\cot^2x}\,dx=∫\frac{\csc^2x}{1+2\cot^2x}\,dx.$ Set$u=\sqrt{2}\cot x.$ Then,$du=−\sqrt{2}\csc^2x$ e a integral é$\displaystyle −\tfrac{1}{\sqrt{2}}∫\frac{du}{1+u^2}=−\tfrac{\sqrt{2}}{2}\tan^{−1}u+C=\tfrac{\sqrt{2}}{2}\tan^{−1}(\sqrt{2}\cot x)+C$. Se alguém usa a identidade$\tan^{−1}s+\tan^{−1}(\frac{1}{s})=\frac{π}{2}$, isso também pode ser escrito$\tfrac{\sqrt{2}}{2}\tan^{−1}(\frac{\tan x}{\sqrt{2}})+C.$

46) [T] Aproxime os pontos nos quais os gráficos de$f(x)=2x^2−1$ e$g(x)=(1+4x^2)^{−3/2}$ se cruzam e aproxime a área entre seus gráficos com precisão de três casas decimais.

47) [T] Aproxime os pontos nos quais os gráficos de$f(x)=x^2−1$ e$f(x)=x^2−1$ se cruzam e aproxime a área entre seus gráficos com precisão de três casas decimais.

Resposta: $x≈±1.13525.$A estimativa do ponto final esquerdo com$N=100$ é 2,796 e esses decimais persistem por$N=500$.

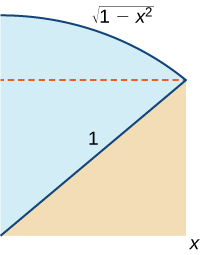
48) Use o gráfico a seguir para provar que$\displaystyle ∫^x_0\sqrt{1−t^2}\,dt=\frac{1}{2}x\sqrt{1−x^2}+\frac{1}{2}\sin^{−1}x.$

$Um diagrama contendo duas formas, uma cunha de um círculo sombreado em azul sobre um triângulo sombreado em marrom. A hipotenusa do triângulo é uma das bordas do raio da cunha do círculo e tem 1 unidade de comprimento. Há uma linha vermelha pontilhada formando um retângulo a partir de parte da cunha e do triângulo, com a hipotenusa do triângulo como a diagonal do retângulo. A curva da circunferência é descrita pela equação sqrt (1-x^2).$