5.5E: Exercícios para a Seção 5.5

1) Por que\(u\) a substituição é chamada de mudança de variável?

2) Se\( f=g∘h\), ao reverter a regra da cadeia\(\dfrac{d}{dx}(g∘h)(x)=g′(h(x))h′(x)\), você deve tomar\( u=g(x)\) ou\(u=h(x)?\)

Responda

\(u=h(x)\)

Nos exercícios 3 a 7, verifique cada identidade usando a diferenciação. Em seguida, usando a\(u\) substituição indicada, identifique de\(f\) forma que a integral assuma a forma\(\displaystyle∫f(u)\,du.\)

3)\(\displaystyle ∫x\sqrt{x+1}\,dx=\frac{2}{15}(x+1)^{3/2}(3x−2)+C;\quad u=x+1\)

4)\(\displaystyle∫\frac{x^2}{\sqrt{x−1}}\,dx=\frac{2}{15}\sqrt{x−1}(3x^2+4x+8)+C,\quad (x>1);\quad u=x−1\)

Responda

\( f(u)=\dfrac{(u+1)^2}{\sqrt{u}}\)

5)\(\displaystyle∫x\sqrt{4x^2+9}\,dx=\frac{1}{12}(4x^2+9)^{3/2}+C;\quad u=4x^2+9\)

6)\(\displaystyle∫\frac{x}{\sqrt{4x^2+9}}\,dx=\frac{1}{4}\sqrt{4x^2+9}+C;\quad u=4x^2+9\)

Responda

\( du=8x\,dx;\quad f(u)=\frac{1}{8\sqrt{u}}\)

7)\(\displaystyle∫\frac{x}{(4x^2+9)^2}\,dx=−\frac{1}{8(4x^2+9)} + C;\quad u=4x^2+9\)

Nos exercícios 8 a 17, encontre a antiderivada usando a substituição indicada.

8)\(\displaystyle∫(x+1)^4\,dx;\quad u=x+1\)

Responda

\(\displaystyle∫(x+1)^4\,dx = \frac{1}{5}(x+1)^5+C\)

9)\(\displaystyle∫(x−1)^5\,dx;\quad u=x−1\)

10)\(\displaystyle∫(2x−3)^{−7}\,dx;\quad u=2x−3\)

Responda

\(\displaystyle∫(2x−3)^{−7}\,dx = −\frac{1}{12(2x−3)^6}+C\)

11)\(\displaystyle∫(3x−2)^{−11}\,dx;\quad u=3x−2\)

12)\(\displaystyle∫\frac{x}{\sqrt{x^2+1}}\,dx;\quad u=x^2+1\)

Responda

\(\displaystyle∫\frac{x}{\sqrt{x^2+1}}\,dx = \sqrt{x^2+1}+C\)

13)\(\displaystyle∫\frac{x}{\sqrt{1−x^2}}\,dx;\quad u=1−x^2\)

14)\(\displaystyle∫(x−1)(x^2−2x)^3\,dx;\quad u=x^2−2x\)

Responda

\(\displaystyle∫(x−1)(x^2−2x)^3\,dx = \frac{1}{8}(x^2−2x)^4+C\)

15)\(\displaystyle∫(x^2−2x)(x^3−3x^2)^2\,dx;\quad u=x^3=3x^2\)

16)\(\displaystyle∫\cos^3 θ\,dθ;\quad u=\sin θ\) (Dica:\(\cos^2 θ=1−\sin^2 θ\))

Responda

\(\displaystyle∫\cos^3 θ\,dθ = \sin θ−\dfrac{\sin^3 θ}{3}+C\)

17)\(\displaystyle ∫\sin^3 θ\,dθ;\quad u=\cos θ\) (Dica:\(\sin^2 θ=1−\cos^2θ\))

Nos exercícios 18 a 34, use uma mudança adequada de variáveis para determinar a integral indefinida.

18)\(\displaystyle∫x(1−x)^{99}\,dx\)

Responda

\ (\ begin {align*}\ displaystylex (1−x) ^ {99}\, dx &=\ frac {(1−x) ^ {101}} {101} −\ frac {(1−x) ^ {100}} {100} +C\\ [4pt]
&=-\ frac {(1-x) ^ {100}} {10100}\ big [100x + 1\ grande] +C\ end {align*}\)

19)\(\displaystyle∫t(1−t^2)^{10}dt\)

20)\(\displaystyle∫(11x−7)^{−3}\,dx\)

Responda

\(\displaystyle∫(11x−7)^{−3}\,dx = −\frac{1}{22(11x−7)^2}+C\)

21)\(\displaystyle∫(7x−11)^4\,dx\)

22)\(\displaystyle∫\cos^3 θ\sin θ\,dθ\)

Responda

\(\displaystyle∫\cos^3 θ\sin θ\,dθ = −\frac{\cos^4 θ}{4}+C\)

23)\(\displaystyle∫\sin^7 θ\cos θ\,dθ\)

24)\(\displaystyle∫\cos^2(πt)\sin(πt)\,dt\)

Responda

\(\displaystyle∫\cos^2(πt)\sin(πt)\,dt = −\frac{cos^3(πt)}{3π}+C\)

25)\(\displaystyle∫\sin^2 x\cos^3 x\,dx\) (Dica:\(\sin^2 x+\cos^2 x=1\))

26)\(\displaystyle∫t\sin(t^2)\cos(t^2)\,dt\)

Responda

\(\displaystyle∫t\sin(t^2)\cos(t^2)\,dt = −\frac{1}{4}\cos^2(t^2)+C\)

27)\(\displaystyle∫t^2\cos^2(t^3)\sin(t^3)\,dt\)

28)\(\displaystyle∫\frac{x^2}{(x^3−3)^2}\,dx\)

Responda

\(\displaystyle∫\frac{x^2}{(x^3−3)^2}\,dx = −\frac{1}{3(x^3−3)}+C\)

29)\(\displaystyle∫\frac{x^3}{\sqrt{1−x^2}}\,dx\)

30)\(\displaystyle∫\frac{y^5}{(1−y^3)^{3/2}}\,dy\)

Responda

\(\displaystyle∫\frac{y^5}{(1−y^3)^{3/2}}\,dy = −\frac{2(y^3−2)}{3\sqrt{1−y^3}}+C\)

31)\(\displaystyle∫\cos θ(1−\cos θ)^{99}\sin θ\,dθ\)

32)\(\displaystyle∫(1−\cos^3 θ)^{10}\cos^2 θ\sin θ\,dθ\)

Responda

\(\displaystyle∫(1−\cos^3 θ)^{10}\cos^2 θ\sin θ\,dθ = \frac{1}{33}(1−\cos^3 θ)^{11}+C\)

33)\(\displaystyle∫(\cos θ−1)(\cos^2 θ−2\cos θ)^3\sin θ\,dθ\)

34)\(\displaystyle∫(\sin^2 θ−2\sin θ)(\sin^3 θ−3\sin^2 θ)^3\cos θ\,dθ\)

Responda

\(\displaystyle∫(\sin^2 θ−2\sin θ)(\sin^3 θ−3\sin^2 θ)^3\cos θ\,dθ = \frac{1}{12}(\sin^3 θ−3\sin^2 θ)^4+C\)

Nos exercícios 35 a 38, use uma calculadora para estimar a área sob a curva usando somas de Riemann à esquerda com 50 termos e, em seguida, use a substituição para resolver a resposta exata.

35) [T]\(y=3(1−x)^2\) acabou\([0,2]\)

36) [T]\(y=x(1−x^2)^3\) acabou\([−1,2]\)

Responda

\(L_{50}=−8.5779.\)A área exata é de\(\frac{−81}{8}\) unidades\(^2\).

37) [T]\(y=\sin x(1−\cos x)^2\) acabou\([0,π]\)

38) [T]\(y=\dfrac{x}{(x^2+1)^2}\) acabou\([−1,1]\)

Responda

\(L_{50}=−0.006399\). A área exata é 0.

Nos exercícios 39 a 44, use uma mudança de variáveis para avaliar a integral definida.

39)\(\displaystyle∫^1_0x\sqrt{1−x^2}\,dx\)

40)\(\displaystyle∫^1_0\frac{x}{\sqrt{1+x^2}}\,dx\)

Responda

\(\displaystyle u=1+x^2,\quad du=2x\,dx,\quad ∫^1_0\frac{x}{\sqrt{1+x^2}}\,dx = \frac{1}{2}∫^2_1u^{−1/2}du=\sqrt{2}−1\)

41)\(\displaystyle∫^2_0\frac{t}{\sqrt{5+t^2}}\,dt\)

(42)\(\displaystyle∫^1_0\frac{t^2}{\sqrt{1+t^3}}\,dt\)

Responda

\(\displaystyle u=1+t^3,\quad du=3t^2,\quad ∫^1_0\frac{t^2}{\sqrt{1+t^3}}\,dt = \frac{1}{3}∫^2_1u^{−1/2}du=\frac{2}{3}(\sqrt{2}−1)\)

43)\(\displaystyle∫^{π/4}_0\sec^2 θ\tan θ\,dθ\)

44)\(\displaystyle∫^{π/4}_0\frac{\sin θ}{\cos^4 θ}\,dθ\)

Responda

\(\displaystyle u=\cos θ,\quad du=−\sin θ\,dθ,\quad \int^{π/4}_0\frac{\sin θ}{\cos^4 θ}\,dθ = -∫_1^{\sqrt{2}/2}u^{−4}\,du = ∫^1_{\sqrt{2}/2}u^{−4}\,du=\frac{1}{3}(2\sqrt{2}−1)\)

Nos exercícios 45 a 50, avalie a integral indefinida\(\displaystyle ∫f(x)\,dx\) com constante\(C=0\) usando\(u\) -substituição. Em seguida, represente graficamente a função e a antiderivada no intervalo indicado. Se possível, estime um valor\(C\) que precisaria ser adicionado à antiderivada para torná-la igual à integral definida\(\displaystyle F(x)=∫^x_af(t)\,dt\), com a extremidade esquerda do intervalo dado.

45) [T]\(\displaystyle∫(2x+1)e^{x^2+x−6}\,dx\) acabou\([−3,2]\)

46) [T]\(\displaystyle∫\frac{\cos(\ln(2x))}{x}\,dx\) em\([0,2]\)

Responda

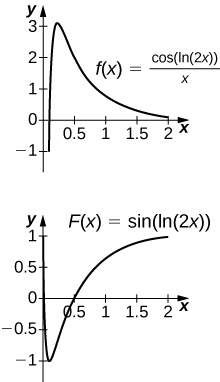
O antiderivado é\(y=\sin(\ln(2x))\). Como a antiderivada não é contínua em\(x=0\), não se pode encontrar um valor de C que faça\(y=\sin(\ln(2x))−C\) funcionar como uma integral definida.

47) [T]\(\displaystyle ∫\frac{3x^2+2x+1}{\sqrt{x^3+x^2+x+4}}\,dx\) acabou\([−1,2]\)

48) [T]\(\displaystyle ∫\frac{\sin x}{\cos^3x}\,dx\) acabou\(\left[−\frac{π}{3},\frac{π}{3}\right]\)

Responda

O antiderivado é\(y=\frac{1}{2}\sec^2 x\). Você deve tomar\(C=−2\) para que\(F(−\frac{π}{3})=0.\)

49) [T]\(\displaystyle ∫(x+2)e^{−x^2−4x+3}\,dx\) acabou\([−5,1]\)

50) [T]\(\displaystyle ∫3x^2\sqrt{2x^3+1}\,dx\) sobre\([0,1]\)

Responda

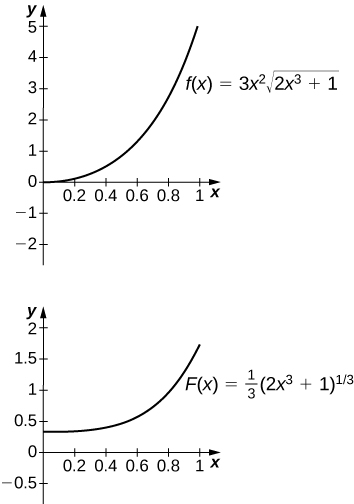
O antiderivado é\( y=\frac{1}{3}(2x^3+1)^{3/2}\). Um deve levar\(C=−\frac{1}{3}\).

51) Se\(h(a)=h(b)\) em\(\displaystyle ∫^b_ag'(h(x))h(x)\,dx,\) que você pode dizer sobre o valor da integral?

52) A substituição\(u=1−x^2\) na integral definida\(\displaystyle ∫^2_0\frac{x}{1−x^2}\,dx\) está correta? Se não, por que não?

Responda

Não, porque o integrando é descontínuo em\(x=1\).

Nos exercícios 53 a 59, use uma mudança de variáveis para mostrar que cada integral definida é igual a zero.

53)\(\displaystyle ∫^π_0\cos^2(2θ)\sin(2θ)\,dθ\)

54)\(\displaystyle ∫^\sqrt{π}_0t\cos(t^2)\sin(t^2)\,dt\)

Responda

\(u=\sin(t^2);\)o integral se torna\(\displaystyle \frac{1}{2}∫^0_0u\,du.\)

55)\(\displaystyle ∫^1_0(1−2t)\,dt\)

(56)\(\displaystyle ∫^1_0\frac{1−2t}{1+(t−\frac{1}{2})^2}\,dt\)

Responda

\(u=1+(t−\frac{1}{2})^2;\)o integral se torna\(\displaystyle −∫^{5/4}_{5/4}\frac{1}{u}\,du\).

57)\(\displaystyle ∫^π_0\sin\left(\left(t−\tfrac{π}{2}\right)^3\right)\cos\left(t−\tfrac{π}{2}\right)\,dt\)

(58)\(\displaystyle ∫^2_0(1−t)\cos(πt)\,dt\)

Responda

\(u=1−t;\)Como o integrando é ímpar, o integral se torna
\[∫^{−1}_1u\cos\big(π(1−u)\big)\,du=∫^{−1}_1u[\cos π\cos u−\sin π\sin u]\,du=−∫^{−1}_1u\cos u\,du=∫_{-1}^1u\cos u\,du=0\nonumber \]

(59)\(\displaystyle ∫^{3π/4}_{π/4}\sin^2 t\cos t\,dt\)

60) Mostre que o valor médio de\(f(x)\) ao longo de um intervalo\([a,b]\) é o mesmo que o valor médio de\(f(cx)\) ao longo do intervalo\(\left[\frac{a}{c},\frac{b}{c}\right]\) para\(c>0.\)

Responda

Configurando\(u=cx\) e\(du=c\,dx\) recebe você\(\displaystyle \frac{1}{\frac{b}{c}−\frac{a}{c}}∫^{b/c}_{a/c}f(cx)\,dx=\frac{c}{b−a}∫^{u=b}_{u=a}f(u)\frac{du}{c}=\frac{1}{b−a}∫^b_af(u)\,du.\)

61) Encontre a área abaixo do gráfico\(f(t)=\dfrac{t}{(1+t^2)^a}\) entre\(t=0\) e\(t=x\) onde\(a>0\) e\(a≠1\) é fixa e avalie o limite como\(x→∞\).

62) Encontre a área abaixo do gráfico de\(g(t)=\dfrac{t}{(1−t^2)^a}\) entre\(t=0\) e\(t=x\), onde\(0<x<1\) e\(a>0\) é fixo. Avalie o limite como\(x→1\).

Responda

\(\displaystyle ∫^x_0g(t)\,dt=\frac{1}{2}∫^1_{u=1−x^2} \frac{du}{u^a}=\frac{1}{2(1−a)}u^{1−a}∣1u=\frac{1}{2(1−a)}(1−(1−x^2)^{1−a})\)Como\(x→1\) o limite é\(\dfrac{1}{2(1−a)}\) se\(a<1\), e o limite diverge para\(+∞\) if\(a>1\).

63) A área de um semicírculo de raio\(1\) pode ser expressa como\(\displaystyle ∫^1_{−1}\sqrt{1−x^2}\,dx\). Use a substituição\(x=\cos t\) para expressar a área de um semicírculo como a integral de uma função trigonométrica. Você não precisa computar a integral.

64) A área da metade superior de uma elipse com um eixo maior que é o\(x\) eixo -de\(x=−1\) a e com um eixo menor que é o\(y\) eixo -de\(y=−b\) para\(y=b\) pode ser escrita como\(\displaystyle ∫^a_{−a}b\sqrt{1−\frac{x^2}{a^2}}\,dx\). Use a substituição\(x=a\cos t\) para expressar essa área em termos de uma integral de uma função trigonométrica. Você não precisa computar a integral.

Responda

\(\displaystyle ∫^{t=0}_{t=π}b\sqrt{1−\cos^2 t}×(−a\sin t)\,dt=∫^{t=π}_{t=0}ab\sin^2 t\,dt\)

65) [T] O gráfico a seguir é de uma função da forma\( f(t)=a\sin(nt)+b\sin(mt)\). Estime os coeficientes\(a\)\(b\) e os parâmetros de frequência\(n\)\(m\) e. Use essas estimativas para aproximar\(\displaystyle ∫^π_0f(t)\,dt\).

66) [T] O gráfico a seguir é de uma função da forma\(f(x)=a\cos(nt)+b\cos(mt)\). Estime os coeficientes\(a\)\(b\) e os parâmetros de frequência\(n\)\(m\) e. Use essas estimativas para aproximar\(\displaystyle ∫^π_0f(t)\,dt.\)

Responda

\(f(t)=2\cos(3t)−\cos(2t);\quad \displaystyle ∫^{π/2}_0(2\cos(3t)−\cos(2t))\,dt=−\frac{2}{3}\)